基于无迹卡尔曼滤波与遗传算法相结合的车辆状态估计∗

周卫琪，齐 翔，陈 龙，徐 兴

(1.江苏大学汽车与交通工程学院，镇江 212013； 2.江苏大学汽车工程研究院，镇江 212013)

前言

近年来，随着汽车保有量的持续增长，消费者对汽车主动安全性要求越来越高。而实时准确地获得汽车的行驶状态是保证车辆主动安全控制的前提。然而，由于传感器的精度与成本的限制和量测噪声的分布特性难以确定等问题，有些状态信息无法找到非常有效适用的传感器来直接进行测量或测量精度不高。比如，纵、侧向速度、轮胎力和质心侧偏角等[1-3]。这种现状对汽车状态信息的精确测量、汽车准确实时控制的实现及汽车控制系统产量化的实现带来了很大的困难，也导致了很多先进的控制算法目前只能停留在理论方面的探讨而未能应用到具体的车辆控制中。对于上述关键状态参数的获取，目前研究中采用软测量，即基于算法进行估计。

目前，汽车状态估计常用算法主要有卡尔曼滤波(KF)[4]、扩展卡尔曼滤波(EKF)[5-6]、无迹卡尔曼滤波(UKF)[7-8]、状态观测器[9]和智能算法如神经网络[10]、模糊逻辑[11]等，这些算法基于车辆模型对汽车的关键状态进行估计。综合分析各种状态估计算法，可以看出各种卡尔曼滤波算法对车辆行驶状态估计的优缺点。经典卡尔曼滤波(KF)只能处理线性系统，而车辆系统是一个复杂的非线性系统，此方法的应用有很大限制。扩展卡尔曼滤波(EKF)估计算法，当估计状态变量出现具有较强非线性或较大的初始估计误差时，则难以取得理想的估计效果，甚至会出现雅克比矩阵无解的情况。UKF估计算法性能优于EKF，且不必计算雅可比矩阵，能提高估计的实时性。但从滤波参数进行考虑，上述常规算法中，过程噪声和量测噪声的统计特性在滤波过程中根据先验值预先设为定值，若噪声水平改变，将会使估计精度降低甚至导致滤波发散。

因此，基于噪声干扰对估计算法精度的影响仍有很大的研究空间。西南交通大学肖建团队利用基于虚拟噪声补偿技术的非线性自适应滤波算法和无迹卡尔曼滤波算法对汽车的行驶状态进行估计[12]。南京航空航天大学魏民祥团队引入蚁群优化算法对汽车状态进行估计，降低噪声的干扰，提高估计精度[13]。因此本文中基于7自由度车辆模型，考虑到系统含有噪声的情况，提出了UKF与遗传算法相结合的方法抑制噪声，提高估计精度。

1 非线性车辆动力学模型

1.1 整车模型

针对汽车行驶过程中关键车辆状态进行估计。首先，在汽车主动安全控制中，车辆纵向、侧向和横摆这3个自由度是需要重点考虑的。其次，为提高模型精度且达到最简化，需要车轮差速控制，因此，须考虑4个车轮的转动自由度。基于以上因素，建立了如图1所示的7自由度车辆模型，相应的车辆动力学方程见式(1)～式(7)。

图1 7自由度车辆动力学模型

式中：vx和vy分别为汽车纵向速度和侧向速度；r为横摆角速度；β为质心侧偏角；m为汽车整车质量；a和b分别为质心到汽车前后轴的距离；Tf和Tr分别为汽车前后轴轮距；Iz为车体绕z轴的转动惯量，Iω为每个车轮的转动惯量；Rω为车轮转动半径；ωij为车轮转动角速度；δ为前轮转角；Fxij和Fyij分别为轮胎纵向力和侧向力；Tbij和Tdij分别为轮胎驱动转矩和制动转矩。

结合状态参数估计思想，将上述汽车动力学模型整理为状态方程和量测方程，状态方程标准形式为

量测方程标准形式为

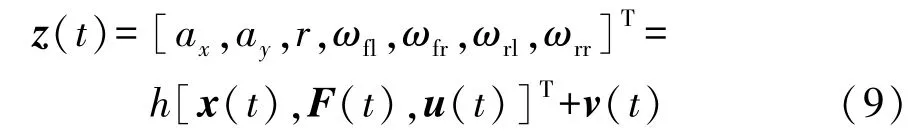
式中：ω(t)为系统状态方程的过程噪声；v(t)为系统量测方程的量测噪声；ax和ay分别为纵向、侧向加速度，其与汽车纵、侧向速度的关系为

根据车辆模型，取

状态向量：x(t)=[vx，vy，r，ωfl，ωfr，ωrl，ωrr]T

控制输入：u(t)=[δ，Tbfl，Tbfr，Tbrl，Tbrr]T

车辆质心侧偏角和纵、侧向速度存在如下关系：

1.2 轮胎模型

根据所建立的车辆模型的特征和所求参数要求，采用“魔术公式”轮胎模型来求取轮胎力。魔术公式轮胎模型可以形式相同的一套公式来描述轮胎的各种力学特性，其基本形式为

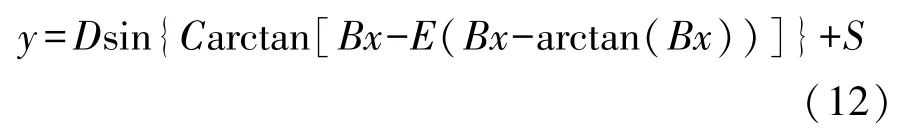
式中：x为轮胎侧偏角；y为轮胎力或力矩；参数B，C，D，E，S与轮胎载荷、车轮外倾角及路面附着条件有关，不同轮胎载荷车轮外倾角及路面附着条件对应不同的系数。其中轮胎侧偏角可从车辆模型得到

2 UKF算法与遗传算法相结合

在建立的非线性7自由度车辆模型的基础上，利用无迹卡尔曼滤波与遗传算法相结合的方法对汽车行驶中的关键状态进行估计。

2.1 UKF算法

UKF是无迹变换(unscented transformation，UT)和标准卡尔曼滤波体系的结合，对于一步预测方程，均值和协方差阵的非线性传递由UT变换进行处理，就变成UKF算法[14]。结合式(8)和式(9)，UKF算法流程如下。

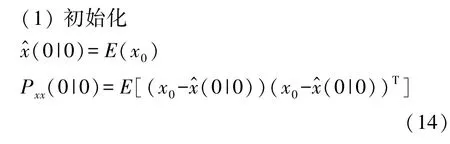
式中x0为初始时刻状态(x(0|0))。

(2)计算采样点集及其相应权值

k时刻比例最小偏度单行采样策略下的采样点集为

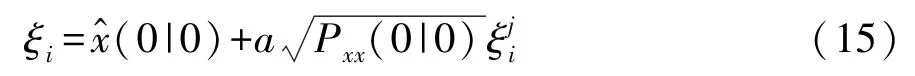
式中：a为取值较小的大于零的比例缩放因子；ξj i为UT变换中Sigma点的迭代公式；分别为均值和方差的权值。

(3)预测更新

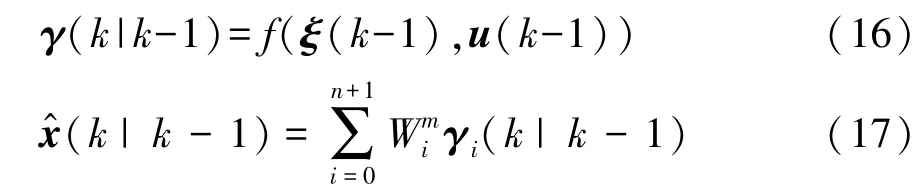
式中：γ(k|k-1)为UT变换中Sigma点带入非线性函数f(·)中得到的点集；γi(k|k-1)为矩阵γ(k|k-1)的第i列，i=0，1，…，n+1。

式中：Qk-1为系统噪声的协方差矩阵。

式中 χi(k|k-1)为矩阵 χ(k|k-1)的第i列，i=0，1，…，n+1。

(4)量测更新

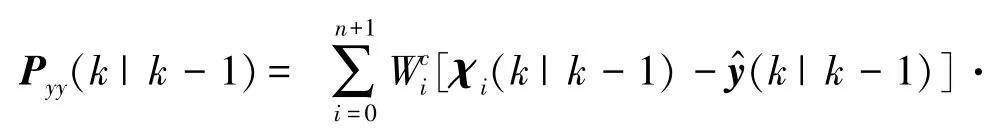
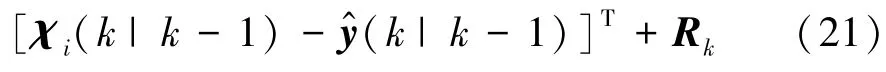
式中Rk为量测噪声的协方差矩阵。

2.2 遗传算法的应用

2.2.1 遗传算法概述

遗传算法(GA)是模拟自然界生物进化的一种随机、并行和自适应的搜索算法，将优化参数表示为编码串群体，根据适应度函数进行选择、交叉和变异等遗传操作[15]。GA从优化问题潜在解集的一个种群开始，该种群由经过基因编码的一定数量的个体组成。初始种群产生后，按照适者生存、优胜劣汰的原理，逐代演化产生越来越好的近似解。在每一代中，根据问题域中个体适应度的大小选择个体，并借助自然遗传学中的遗传算子进行交叉、变异，产生新的解集的种群。该过程将导致种群后代比前代更适应环境，末代种群中的最优个体经过解码即可作为优化问题的最优解。

2.2.2 遗传算子的操作

在选择遗传算子时，根据每个个体的适应度值，采用竞赛法，从上一代群体中选择一个优良的个体遗传到下一代群体中，这样适应性强的个体为下一代个体贡献一个或多个后代的概率更大。杂交操作能得到一个新的个体，新的个体结合了父辈个体的特性。变异操作能对群体中的每一个个体，以某一概率改变某一个或某一些基因值。

2.2.3 基于GA的UKF状态估计

由上述的状态方程可知，其状态变量为[r，β，v，ωij]T，UKF对应的过程噪声协方差矩阵Q和量测噪声协方差矩阵R是GA待优化的参数。二者作为优化参数，自适应得到最优参数。首先，采用二进制编码，求解精确到4位小数，自变量的取值范围为[0，1]，则 8192=213＜104≤214=16384，总染色体长度设为40；令种群大小为30，随机产生一组个体。其次，选取新息的实际方差为适应度函数，以其值最小为目标进行寻优。再采用轮盘赌选择、单点交叉和基本位变异进行遗传操作，交叉率为0.9，变异率为0.1。适应度函数为

式中：h为状态信息的实际方差；y＾(k|k-1)为 UKF滤波的新息序列[13]。加入遗传算法后，基于GA的UKF算法可对过程噪声和量测噪声进行在线优化。提出的基于GA的UKF状态估计流程如图2所示。

图2 基于GA的UKF算法流程

其中，流程中的关键步骤在于对Q和R的初始化，其次采用GA对Q和R进行优化，自适应得到最优参数。

3 仿真与试验验证

3.1 仿真验证

为验证算法的有效性，采用CarSim与Simulink联合仿真。仿真中采用的某车型参数如表1所示。为模拟极限工况下汽车的操纵性，选用工况为急剧双移线，如图3所示。在CarSim中将路面附着系数设置为 0.5，车速设置为 80km/h，采样时间为0.01s。由CarSim中所选取的车辆模型向滤波估计算法提供输入，算法的输入包括系统控制输入，即前轮转角δ和轮胎制动力矩Tbij；测量输出，即纵向加速度ax、侧向加速度ay、横摆角速度r和4个车轮转速ωij。为模拟系统在运行过程中量测噪声特性变化的情况，在系统各测量输出端叠加方差变化的零均值高斯白噪声，如图4～图7所示。急剧双移线中由UKF和GA/UKF算法估计的汽车纵向速度、侧向速度、质心侧偏角和部分轮胎力的估计值如图8～图14所示。

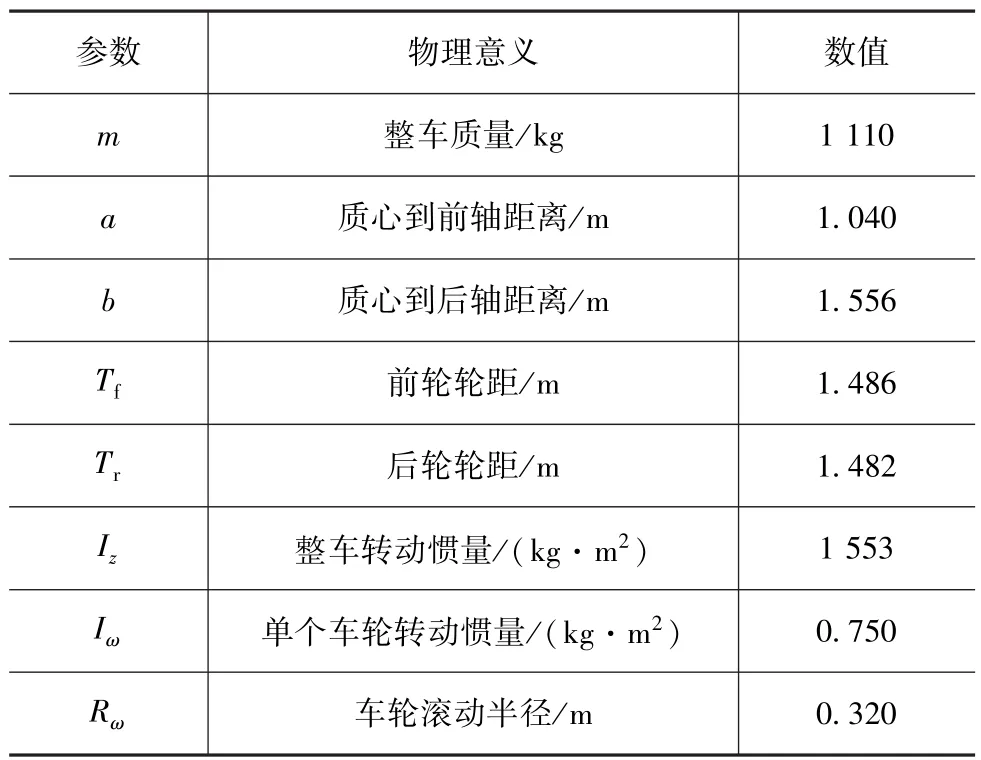
表1 整车参数

图3 汽车行驶路径

图4 叠加到纵、侧向加速度的噪声

从仿真结果可知，利用UKF算法估计的汽车纵向车速、侧向车速、质心侧偏角和轮胎的侧向力结果与真实值相比会出现较大偏差，尤其是在峰值位置。而GA/UKF则能降低噪声或车辆模型本身带来的误差，提高估计精度，降低噪声的干扰。

图5 叠加到左前轮、右前轮转速的噪声

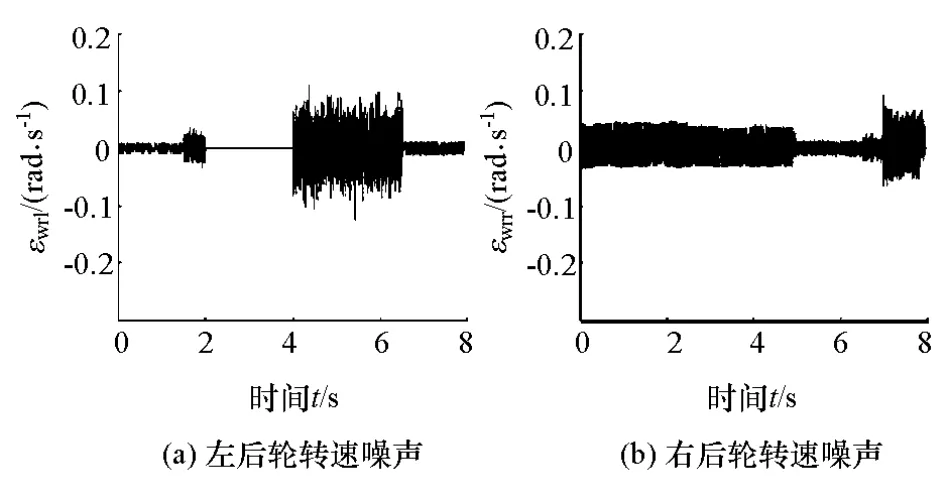
图6 叠加到左后轮、右后轮转速的噪声

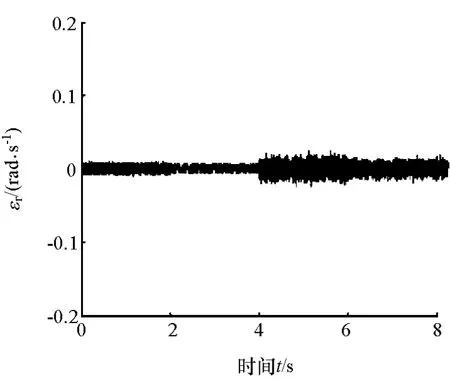
图7 叠加到横摆角速度端的噪声

图8 纵向车速估计对比

图9 侧向车速估计对比

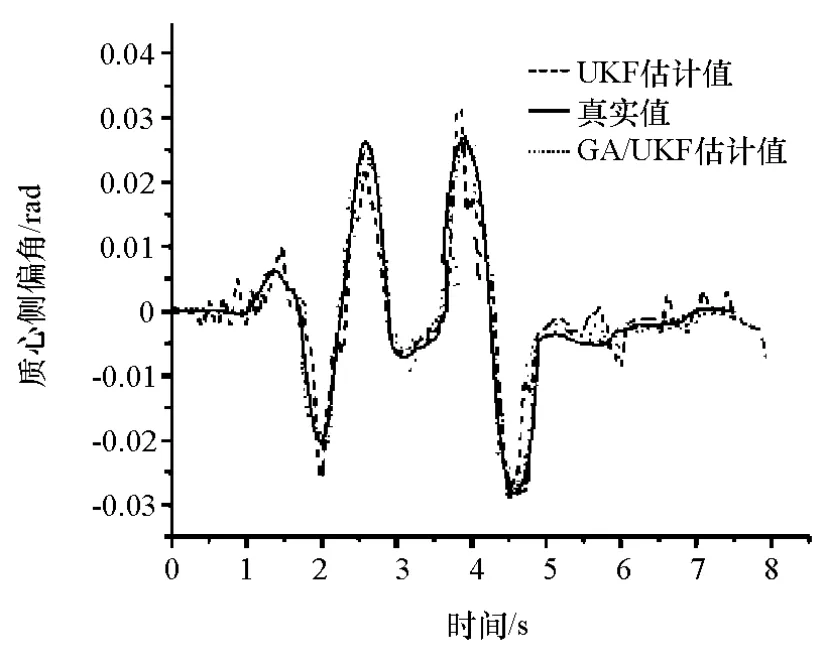
图10 质心侧偏角估计对比

图11 左前轮侧向力估计对比

图12 右前轮侧向力估计对比

汽车在行驶过程中会不可避免地遇到一定程度的干扰，对传感器造成一定影响，导致传感器的统计特性难以准确获得，具有很大的随机性。

图13 左后轮侧向力对比

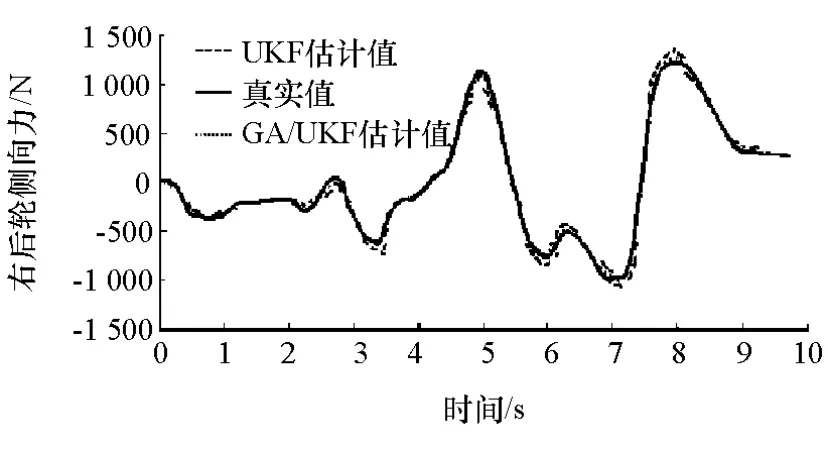
图14 右后轮侧向力对比

GA/UKF利用UKF算法的新息序列在线估计量测噪声的统计特性，有效降低未知或时变噪声对汽车状态估计的影响，对噪声具有更强的抑制能力。因此，GA/UKF具有更好的精确度和工程价值。

统计计算出参数估计值相对于CarSim仿真结果的平均绝对误差(MAE)和均方根误差(RMSE)，对UKF和GA/UKF这两种算法的估计精度进行定量的比较，表2中列出了部分参数，即纵向车速、侧向车速、质心侧偏角和左前轮侧向力的 MAE和RMSE指标。

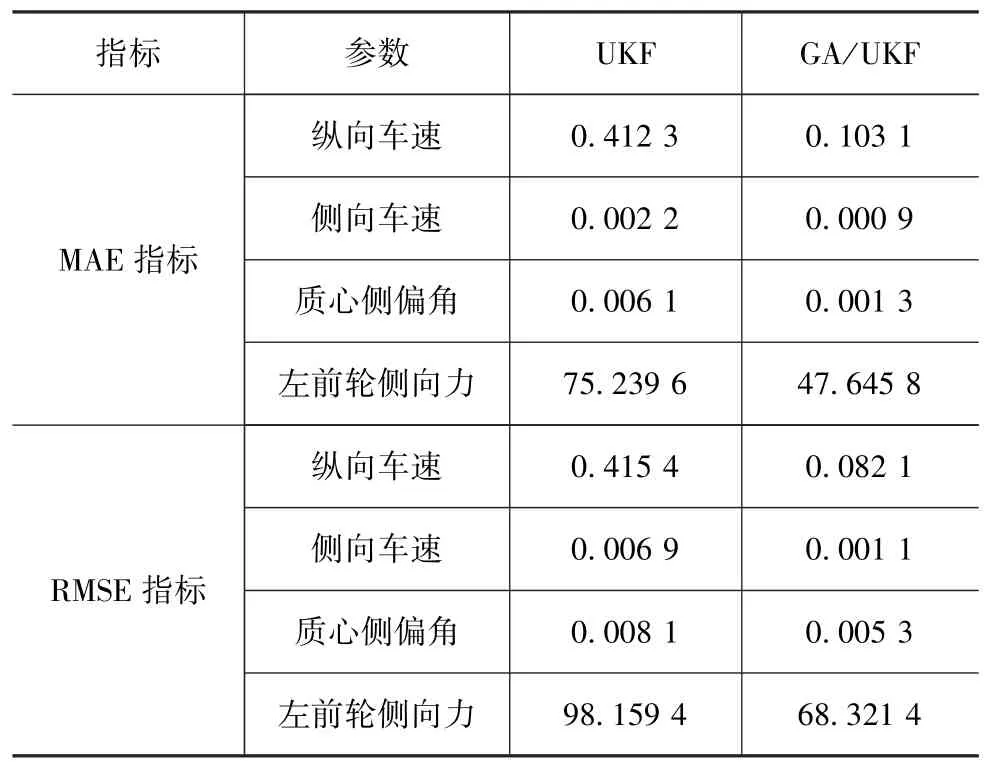
表2 UKF和GA/UKF的MAE和RMSE指标

从表2可以看出，基于GA/UKF和状态参数模型估计出来的纵向车速、侧向车速、质心侧偏角以及轮胎侧向力的MAE和RMSE指标比UKF小很多，说明GA/UKF具有更高的估计精度。

3.2 实车验证

为验证提出的车辆状态估计算法的准确性，对某车型轿车进行了在ISO双移线(ISO 3888—1)工况下的实车试验。试验车上安装了陀螺仪、非接触式速度传感器、加速度传感器和转向盘转角传感器等，分别用来采集横摆角速度、纵向车速、侧向车速、纵向加速度、侧向加速度和转向盘转角。

用于模拟道路工况的底盘测功机及其试验系统如图15和图16所示。底盘测功机监控系统用来记录保存汽车车速、加速度和轮胎力等信息。CAN总线用来采集上述所有传感器信号和控制信号。快速原型是一套基于产品ECU和Matlab/Simulink的控制系统开发的软硬件平台[16]，基于快速原型实现对整车的控制。

图15 底盘测功机

图16 基于底盘测功机的道路模拟试验系统

图17～图19为横摆角速度、纵向车速和侧向车速3个状态量的GA/UKF估计值、UKF估计值与实车试验值的比较。由图可以看出，UKF估计值相对精度较低，GA/UKF估计值与试验值虽也存在小偏差，但在总体上均保持着较高的一致性。因此，在基于较高精度车辆模型的前提下，采用GA/UKF算法得到的估计结果达到了较高的精度。此外，在试验车进行测试时，传感器安装位置的偏差也是估计值与测试值产生误差的一个重要因素。

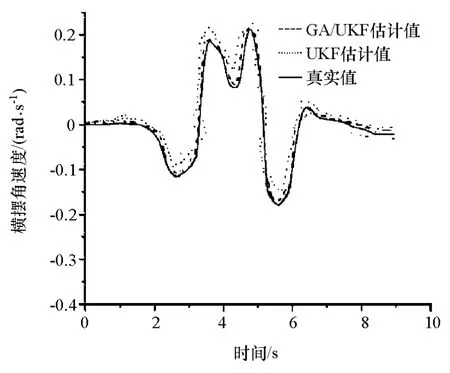
图17 横摆角速度的估计值与试验值对比

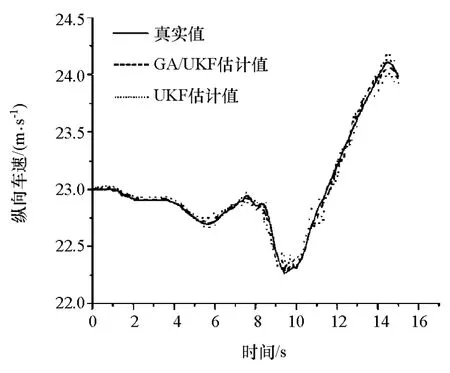
图18 纵向车速的估计值与试验值对比

图19 侧向车速的估计值与试验值对比

4 结论

(1)提出基于7自由度车辆模型的GA/UKF状态估计算法，对汽车行驶过程中状态参数进行估计。GA/UKF算法中，由于遗传算法的寻优作用，可以降低系统过程噪声和量测噪声对估计结果的影响，大大减小了估计结果与真实值之间的误差，使得到的估计值精度更高。

(2)在基于7自由度车辆模型的基础上，提高模型精度，可利用较低成本的传感器对较易测量的转向盘转角、纵侧向加速度、横摆角速度等进行测量，而对其它多种参数进行估计。

(3)仿真和实车试验表明，相比于单纯的UKF算法，GA/UKF算法的估计结果与试验真实值有更好的一致性，具有更高精度和抗干扰性。但是，由于试验条件和工作量的原因，本文试验工况不具备普遍性，今后将在更多的工况，如蛇形和单移线等工况进行研究。