基于随机森林的驾驶人驾驶习性辨识策略∗
朱 冰,李伟男,汪 震,赵 健,何 睿,韩嘉懿
(1.吉林大学,汽车仿真与控制国家重点实验室,长春 130022; 2.吉林大学,工程仿生教育部重点实验室,长春 130022)
前言
驾驶人驾驶习性(driving style),是指驾驶人相对稳定的和习惯性的内在驾驶行为倾向,它是个体驾驶人心理思维和行为模式的综合表征,不同驾驶人之间驾驶习性差异明显,典型的驾驶习性包括激进型、一般型和保守型等[1-2]。深入理解驾驶人驾驶习性及其表征方法,建立高精度驾驶人驾驶习性辨识模型,对于实现在汽车自动驾驶、辅助驾驶和主动安全等不同控制系统下的人机和谐交互具有重要意义。
早在20世纪70年代,国外学者即开始关注驾驶人驾驶习性的研究。WAHAB A等学者认为,由于驾驶人潜意识工作方式的差异,每个驾驶人从潜意识到有意识的思维转换是独一无二的,因此每个驾驶人自然地具有不同的驾驶习性[3]。LU J等人引入模糊控制理论对驾驶人驾驶习性进行了初步的分类[4]。
国内对于驾驶人驾驶习性的研究起步较晚,但经过十余年的积累也有了一定的成果。清华大学王建强教授通过驾驶人释放加速踏板和开始制动时刻的碰撞时间TTC(time to collision)数据聚类分析,将驾驶人分为谨慎型、正常型和侵略型3类[5]。长安大学毛锦根据真实车辆道路驾驶数据,使用多因素模糊数学分类法,基于跟车时距、最小跟车时距、换道时距、超速频次和换道过程转向盘最大转角与车速的拟合结果等5个参数,将驾驶习性分为冒进型、比较冒进型、比较谨慎型和谨慎型4类[6]。
这些相关研究在驾驶习性表征与辨识等方面已经有所进展,然而,复杂多变的驾驶习性因人与工况而异。传统研究中往往对驾驶习性进行单纯的主观标定,训练样本标签以及辨识结果的准确性难以保证;此外,驾驶数据变量复杂多样,需要基于重要性对其进行有效筛选,从而在保障辨识精度的前提下简化模型结构。
为深入研究驾驶人驾驶习性的有效表征方法及辨识策略,本文中搭建驾驶人驾驶习性实车数据采集平台,采集驾驶人在典型跟车工况下的驾驶数据;应用凝聚层次聚类方法对驾驶人驾驶习性进行标定;采用随机森林算法对驾驶数据各个变量的重要性进行分析,选取对模型辨识精度贡献起主导作用的变量进行随机森林模型训练;最后,采用留一法对测试驾驶人进行驾驶习性辨识测试,验证辨识模型的辨识效果。
1 驾驶人驾驶习性数据采集
1.1 实车数据采集平台
为了实时采集驾驶人在实际驾驶状态下的驾驶数据,搭建了实车数据采集平台,如图1所示。采集平台由一辆主车和一辆交通车组成,两车内分别布置有相应的仪器设备用于自车、车-车之间运动状态和运动姿态等驾驶习性相关数据的实时采集。

图1 实车数据采集平台
实车数据采集平台原理如图2所示。通过主车CAN总线实时采集制动主缸压力、加速踏板行程和转向盘转角等驾驶人操控信息;通过Oxford Technical Solutions公司的RT3002组合导航系统精确测量本车的车速、加速度等状态信息;通过RT-Range实现两个车辆之间的相对距离、相对车速等相对状态信息的精确测量。采集得到的驾驶数据通过CAN总线传输到dSpace MicroAutoBox进行时间同步,进而通过以太网电缆传输至工控机进行存储。
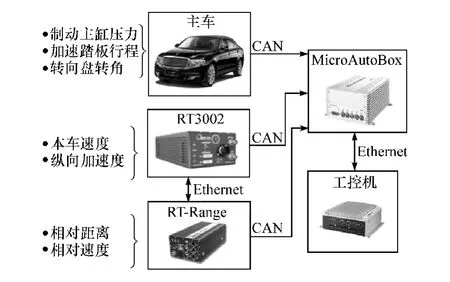
图2 实车数据采集平台原理
1.2 工况设计
驾驶人驾驶习性数据采集工况应该能够在最大程度上激励出不同驾驶人的差异化驾驶习性,经过多组试验对比,发现当前车车速变化时间历程表现为“加-减-加”时,后车驾驶人的驾驶数据差异最为明显。
最终选取单车道直线结构化沥青道路进行测试。测试时,前车车速变化曲线如图3所示。前车按照0-70-40-70km/h的速度行驶,期间依次历经加速、匀速、减速、匀速、加速和匀速等不同的行驶状况,以尽可能激励后车驾驶人驾驶习性。后车首先按照被测驾驶人习惯运动至与前车相距一定距离的位置,随后被测驾驶人按照自己习惯的驾驶方式进行跟车驾驶。

图3 目标车速度时间历程曲线
1.3 被测驾驶人
试验通过社会招募方式,共招募了34名驾驶人进行驾驶习性数据采集试验,其基本信息如表1所示。其中,男性驾驶人28人,女性驾驶人6人;驾驶人年龄范围为22-50周岁,平均年龄为34.5周岁;驾龄范围为1-17年,平均驾龄为4.7年。
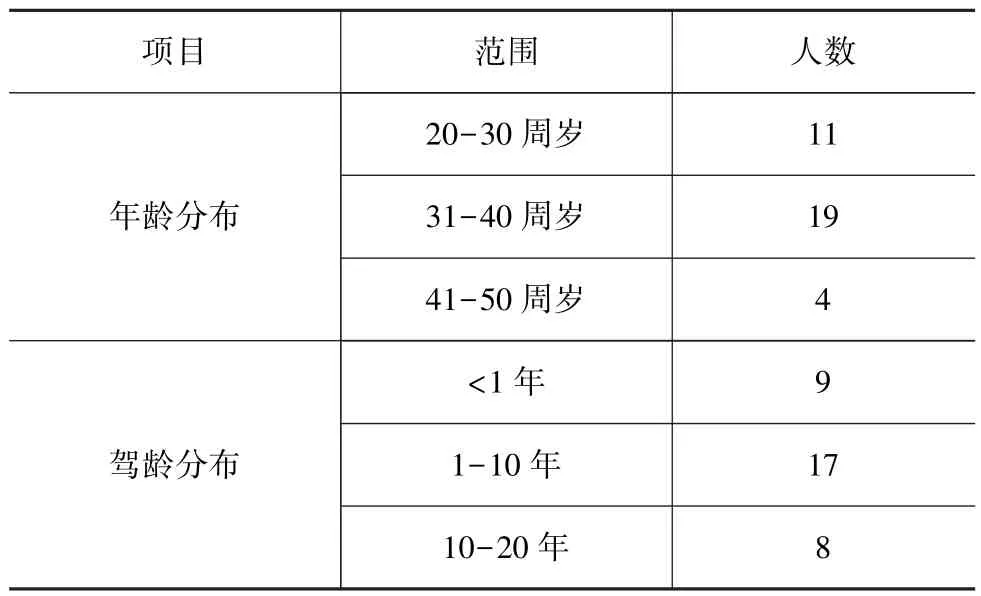
表1 被测驾驶人基本信息
2 驾驶人驾驶习性表征
驾驶人驾驶习性具有很强的不确定性,本文中采用层次聚类方法对驾驶人驾驶数据进行分析,以期将驾驶习性相近的被测驾驶人凝聚为关系紧密的簇[7-8],并利用簇的关系实现驾驶习性的准确表征。
选取与纵向跟车行为密切相关的制动主缸压力最大值X1、加速踏板位置最大值X2、纵向加速度最大值X3、相对距离平均值X4、相对速度平均值X5、相对速度最大值X6和车头时距平均值X7等7组参数进行分析。其中车头时距表示前后两辆车的前端通过同一地点的时间差,可通过两车相对距离除以后车速度计算得到。
得到的原始驾驶数据样本集T为
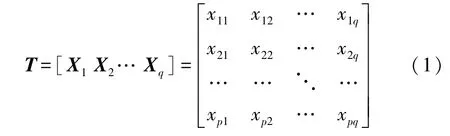
式中:p=34,q=7。
为便于聚类分析,首先对驾驶习性数据进行归一化处理,归一化后的样本集为
Y=(yij)p×q

式中:i=1,2,…,34;j=1,2,…,7;xjmin和xjmax分别为第j列驾驶数据的最大值和最小值。
采用基于离差平方法的凝聚层次聚类方法对同类驾驶习性原子簇进行合并,即具有相似特征的驾驶习性数据样本之间的离差平方和应较小,而驾驶习性特征差别较大的样本之间的离差平方和应较大。
假定在凝聚层次聚类过程中,将p个驾驶习性数据样本分成k个类别G1,G2,…,Gk,用 Yti(1≤t≤k)表示类别Gt中的第i个驾驶习性数据样本向量,nt表示类别Gt中数据样本的个数,表示类别Gt中数据样本的向量均值,则类别Gt中数据样本的离差平方和St的计算公式为

对p个驾驶习性数据样本进行凝聚层次聚类遍历求解,选择使离差平方和增加最小的两类(即驾驶习性最为相似的两类)进行合并,直到所有的样本归为一类,聚类过程如图4所示。驾驶习性相近的被测驾驶人不断被凝聚到同一个簇中,每个簇对应不同风格的驾驶习性。
对应图4中3个最大的簇,将驾驶习性数据样本最终凝集聚类为3组,结合3个簇内部驾驶数据的共性特征,层次聚类结果如表2所示。

表2 层次聚类结果
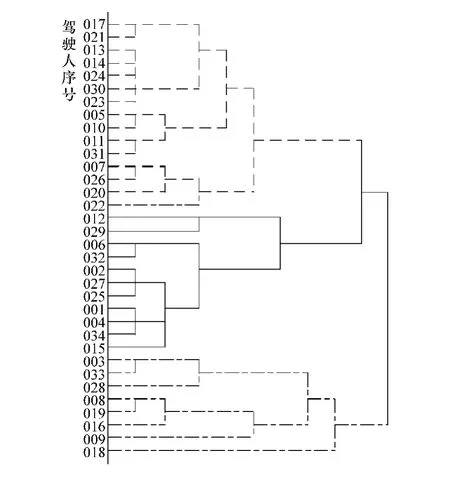
图4 驾驶习性数据样本层次聚类过程
分别绘制3类不同驾驶习性驾驶人相对车速-相对距离统计分布如图5所示。
可见,保守型驾驶人由于驾驶行为较为谨慎,跟车过程中相对距离较大,相对距离在20m以上的占比达96%,同时,保守型驾驶人的相对速度大部分为正值(即本车速度小于前车速度),占比达64%。
激进型驾驶人则跟车距离较近,相对速度多为负值,占比达71%;一般型驾驶人的驾驶数据位于二者之间。
3 驾驶人驾驶习性辨识模型
在对驾驶人驾驶习性进行准确表征的基础上,引入随机森林算法构建驾驶人驾驶习性辨识模型。随机森林模型(random forest model)是利用多棵决策树对样本进行训练并预测的一种分类器,其对异常值和噪声有很强的容忍度,并可以在分析数据的同时给出各个变量重要性的评分(variable importance measure, VIM)[9-10]。
3.1 基于Gini指数的各属性变量重要性分析
采用Gini指数分析各驾驶习性数据变量对驾驶人驾驶习性辨识精度的影响。对于驾驶数据样本集T,其Gini指数定义为
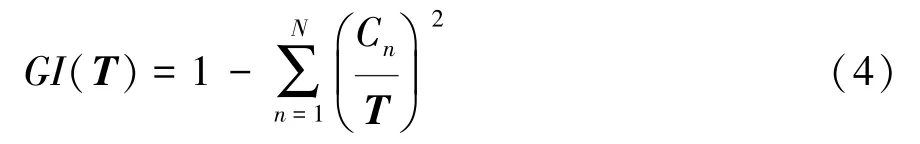
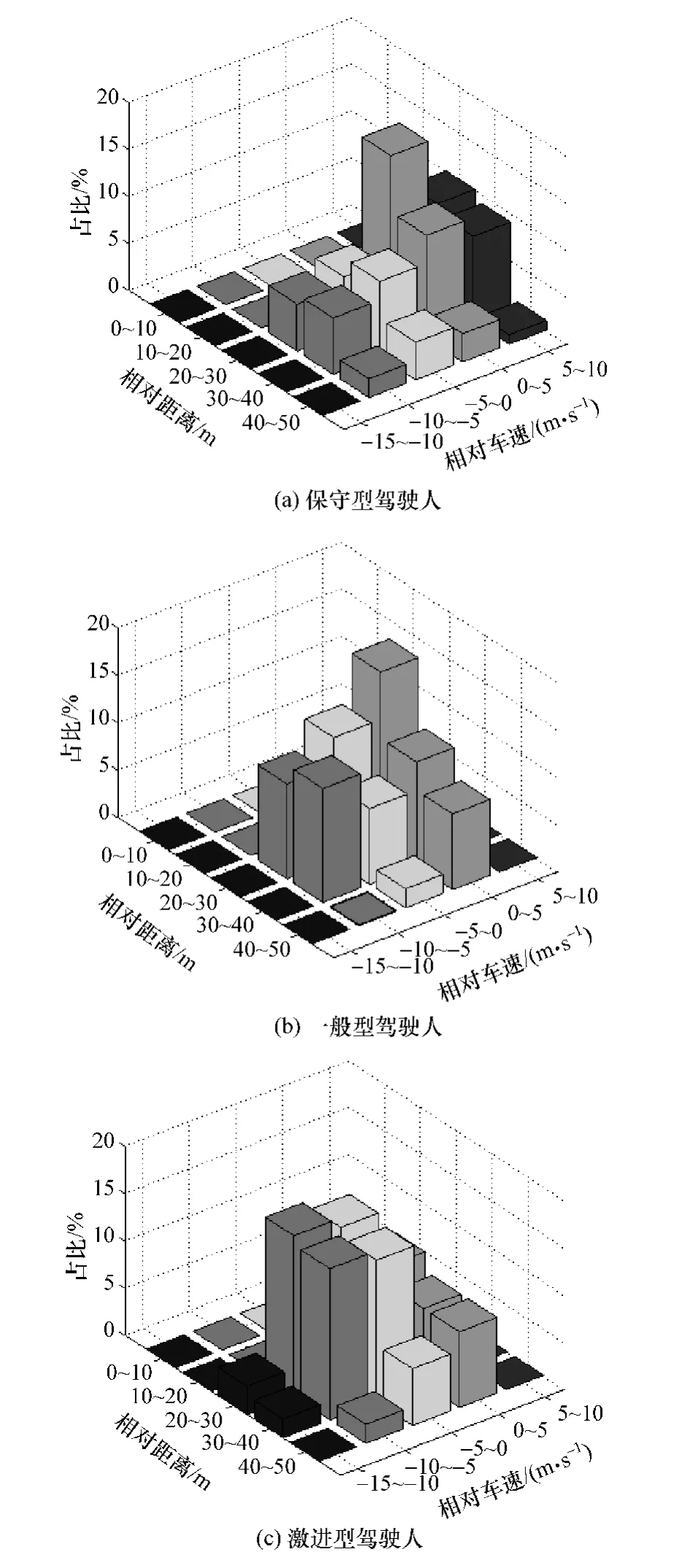
图5 不同驾驶习性驾驶人相对车速-相对距离统计分布
式中:N为驾驶习性类别,取N=3,分别代表保守型、一般型和激进型驾驶习性;Cn表示样本集T中属于第n类驾驶习性的样本子集。
如果依照某一驾驶数据变量Xj(1≤j≤7)将驾驶数据样本集 T 分为b个部分,即 T1,T2,…,Tb。那么在属性变量Xj的条件下,集合T的Gini指数定义为

驾驶数据变量Xj在随机森林模型中任一节点m处的重要性可以用节点m分枝前后Gini指数变化量来表示:
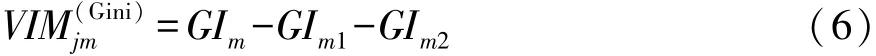
式中:GIm,GIm1和GIm2分别为节点m分裂前和分裂成2个新节点的Gini指数。
如果驾驶数据变量Xj在随机森林模型中的第e棵树中出现过M次,则变量Xj在第e棵树中的重要性为

因此,驾驶数据变量Xj在整个随机森林模型中的重要性可以表示为
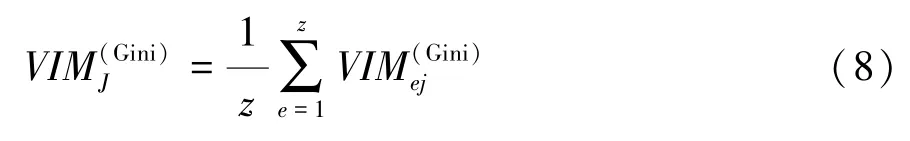
式中z为随机森林模型中决策树的棵数,即分类器的数量。
计算、绘制驾驶人驾驶习性数据集中各个变量参数的Gini重要性散点图,如图6所示。

图6 Gini重要性散点图
可见,在纵向跟车工况下,不同的驾驶习性数据变量对于随机森林模型辨识精度的重要性会有所差别,各个变量参数对驾驶人驾驶习性辨识模型辨识精度的重要性依次为:加速踏板位置最大值X2>车头时距平均值X7>相对距离平均值X4>相对速度最大值X6>纵向加速度最大值X3>主缸压力最大值X1>相对速度平均值X5。
其中,加速踏板位置最大值X2、车头时距平均值X7和相对距离平均值X43个变量对模型辨识精度的影响相对其它几个变量要更加明显,说明这3组参数更能体现驾驶人在跟车过程中的驾驶习性。
3.2 基于变量重要性的随机森林模型
在尽可能不影响辨识精度的前提下,选用更少的变量训练随机森林模型可以有效降低模型的复杂度,缩短运算时间。因此,基于变量重要性分析,选取加速踏板位置最大值、车头时距平均值和相对距离平均值3个变量建立随机森林模型,其训练原理如图7所示[11]。

图7 随机森林模型训练原理
随机森林模型具体实现流程如下。
步骤1:在p个驾驶习性数据样本中,有放回地随机选择p个样本(即允许其中存在重复的样本)形成1个自动样本集,利用这个样本集训练1棵决策树。
步骤2:在决策树的每个节点需要分裂时,随机从加速踏板位置最大值、车头时距平均值和相对距离平均值3个属性变量中选取出r个属性(r<3),针对选出的每一个属性遍历所有可能的分裂方法,并分别求取其Gini指数,最终选择具有最小Gini指数的属性作为该节点分裂属性。按此方法确定决策树的每个节点,直到不能够再分裂为止。
步骤3:重复步骤1和步骤2,得到z棵决策树,构成用于驾驶习性辨识的随机森林模型。
这里,步骤1中有放回地随机选取样本以及步骤2中随机选取r个属性会使得决策树的相关性显著降低。这两个过程中的随机性和不确定性,可以使随机森林模型不会随着分类树数目的增加而产生过度拟合的问题。
利用训练得到的随机森林模型可以进行驾驶人驾驶习性辨识。辨识时,模型中每一棵决策树对输入的驾驶数据进行投票,计算各类驾驶习性(保守型、一般型和激进型)获得的投票数,最终得票数最高的即为所输入的驾驶数据对应的驾驶人驾驶习性。
3.3 测试验证分析
采用留一法(leave-one-out)对提出的驾驶人驾驶习性辨识模型进行测试验证分析,即逐一将34个驾驶习性数据样本划分为两个子集,第一个子集包含33个样本用来训练辨识模型,另一个子集包含1个样本用来测试验证,如此,从001到034号被测驾驶人的驾驶数据都可以得到有效的辨识测试,测试验证原理如图8所示。

图8 留一法测试验证原理
取300棵决策树建立随机森林模型进行测试,测试结果如表3所示。针对保守型、一般型和激进型驾驶习性所建立的随机森林模型辨识的正确率分别为100%,100%和87.5%;随机森林模型整体精准度达到97.1%。可见,所建立的基于变量重要性的随机森林模型可以有效辨识驾驶人驾驶习性。

表3 测试结果
为进一步分析随机森林模型辨识性能,分别采用基于Gini重要性分析获取的3个特征变量以及全部的7个特征变量训练随机森林模型,并从5棵开始逐渐增加随机森林模型中决策树的数目进行测试,得到模型整体精准度随决策树数量变化的结果,如图9所示。
可见,当随机森林模型中决策树的数目较少时,模型整体精准度会随着决策树棵数的增加而提升。但当决策树超过300棵后,模型整体精准度不但不会继续提升,还会使模型过于复杂、增加计算量。此外,当随机森林模型中决策树的数目较少时,采用7个特征变量训练的驾驶习性辨识模型的整体精准度会略高,但当决策树超过200棵后,两种模型的精度几乎一致,采用基于变量重要性的随机森林模型会更加简单易行。
4 结论
本文中提出了一种基于随机森林模型的驾驶人驾驶习性辨识策略。首先,搭建了实车数据采集平台,并设计了能最大程度激励出不同驾驶人差异化驾驶习性的试验工况,采集了驾驶人跟车过程中的典型驾驶数据。然后,采用层次聚类方法,将驾驶习性相近的被测驾驶人驾驶数据凝聚为关系紧密的3个簇,对应3种类型:保守型、一般型和激进型。在此基础上,引入随机森林模型理论,基于Gini指数对各属性变量重要性进行了分析,建立了基于变量重要性的随机森林模型。最后,采用留一法对辨识模型进行了测试验证分析。结果表明,本文中建立的辨识模型可以有效地辨识驾驶人驾驶习性,模型整体精准度可以达到97.1%。当随机森林模型中决策树的数目较少时,模型整体精准度会随着决策树棵数和特征变量的增加而提升;但当决策树超过一定数量后,这些影响将显著降低,采用基于变量重要性的随机森林模型会更加简单易行。

