商用车鼓式制动器热衰退性能台架试验研究

曾繁卓,李伟,王应国,雷文,任学良,翟翊

(中国汽车工程研究院股份有限公司,重庆 401122)

0 引言

目前，重型商用车普遍安装气压鼓式制动器，与其他结构的制动器相比，它具有制动力矩大、结构相对简单以及价格便宜等优势，但是频繁制动后鼓式制动器的温升会导致制动效能急剧下降，出现制动热衰退现象的缺点也十分明显，这种现象在车辆超载、超速行驶时更为显著[1]。调查发现，重型商用车出现制动失效的故障绝大部分是由热衰退引起的。因此，探究车辆载荷、行驶速度和制动距离对制动热衰退的影响尤为重要。

国内对鼓式制动器热衰退的研究主要是通过选定某一试验车型在某典型高速公路的长下坡路段进行实地测试，记录制动鼓表面的温度，分析制动鼓温度与坡长、坡度、车速和车重的关系。这类研究的不足之处在于测试过程情况复杂，一致性难以保证；另外，实车测试只能记录制动鼓外表面的温度，缺乏对热衰退过程中制动力矩的监测。此次研究结合汽车行业标准QC/T 239-2015《商用车辆行车制动器技术要求及台架试验方法》，应用重型商用车制动器惯性试验台架，模拟东风某重型商用车的气压鼓式制动器在长下坡持续制动工况下，分析车速、载荷和制动距离对制动器温升的影响。

1 试验设计

根据顾永田[2]对312国道马家坡和蓝小路两个长下坡路段所经过车辆的统计分析中发现，货车生产厂家中东风商用车占比高达71%，货车轴型中三轴载货车比例为42%。因此，此次选用东风商用车公司生产的某三轴车型的鼓式制动器作为研究对象具有一定的普遍性。结合苏波等人[3]根据跟车及问卷调查，发现大货车在长下坡路段车速为40～65 km/h，并且下坡过程中基本能保持匀速状态。因此，试验车速拟设定为40、50、60和70 km/h。台架试验所需参数如表1所示。

表1 试验参数

1.1 试验准备

1.1.1 试验台主轴转速的计算

制动器惯性试验台主轴转速与车速按如下关系换算：

n=2.65v/r

式中：n为制动器惯性试验台主轴转速，r/min；v为试验车速，km/h；r为车轮滚动半径，m。

根据上述公式，计算得到试验车速对应的转速如表2所示。

表2 试验转速

1.1.2 试验转动惯量的计算

试验转动惯量按下式进行计算：

I=mr2

式中：I为转动惯量计算值，kg·m2；m为将汽车最大设计总质量按制动力分配比设计值分配给被试制动器所对应车轮承受的那部分质量，kg；r为车轮滚动半径，m。

经过上述公式计算得到制动器满载和超载时的试验转动惯量，如表3所示。

表3 试验转动惯量

1.2 热电偶的安装方式

引起热衰退现象的主要因素是制动器温度的上升使制动力矩急剧衰减，因此摸清热衰退过程中制动蹄片和制动鼓的温度变化尤为重要。参照QC/T 556-1999《汽车制动器 温度测量和热电偶安装》的具体要求，并结合此次研究的重点，分别在制动衬片表面、制动蹄背钢板面、制动鼓内表面和制动鼓外表面安装K型热电偶(测温范围：-40～1 300 ℃)。

在靠近制动衬片长宽方向的中心处钻两个5 mm的通孔(注意一定要避开筋和散热片)，将热电偶测量端固定在孔内，偶头距离制动衬片摩擦表面和制动蹄背钢板面都为1 mm。在制动鼓摩擦面宽度方向的中心钻两个相对于鼓中心对称的5 mm通孔，将热电偶测量端固定在孔内，偶头距离制动鼓内、外表面为0.3～0.5 mm[4]。制动器安转位置和制动器试验台架分别如图1和图2所示。

图1 制动器安转位置

图2 制动器试验台架

1.3 试验方法与步骤

由于制动器制动衬片表面与制动鼓内表面的贴合程度对制动力矩产生很大影响，因此，试验开始前必须保证制动鼓内表面的圆跳动控制在10丝以内，制动衬片与制动鼓内表面的间距约为0.5 mm。同时，在进行模拟长下坡持续制动的热衰退试验开始前，需要先进行磨合试验，保证制动衬片与制动鼓内表面接触良好。

长下坡持续制动的热衰退试验主要模拟在长下坡路段汽车持续较长时间重复制动以达到控制车速的目的。目前，重型商用车的额定工作气压已经普遍提高到1.0 MPa，为了能够更真实地还原持续频繁制动过程，试验气压设置为0.7 MPa，制动周期设置为1 min，各种速度下进行15次全制动，同时记录制动力矩、制动蹄片和制动鼓的温度。

1.3.1 磨合试验

(1)制动初速度50 km/h；

(2)试验冷却风速11 m/s，冷却空气的温度为室温；

(3)调整制动管路压力，使制动减速度达到0.3g，从制动初速度进行制动，到终速度为零；

(4)制动间隔时间以控制制动器初温不超过100 ℃而定；

(5)磨合次数以使制动衬片与制动鼓之间的接触面积达到80%以上而定，磨合试验次数一般设置为500次。

1.3.2 模拟长下坡持续制动的热衰退试验

(1)制动初速度40、50、60、70 km/h；

(2)采用恒定输入方式进行试验，调整控制气压为0.75 MPa，从制动初速度进行制动，到终速度为零；

(3)首次制动温度不高于60 ℃，在第一次制动进行前关闭试验台冷却系统，整个试验过程中不对制动器吹风降温；

(4)制动周期设置为1 min；

(5)各种速度下各进行15次全制动。

2 数据处理与分析

根据戈若愚等[5]通过实车测试发现影响制动鼓温度的因素主要包括车辆载重、行驶速度、坡长和坡度。由于台架试验的限制无法模拟坡度，因此文中主要从车辆载荷、行驶车速、制动距离这3个方面进行分析。从模拟长下坡持续制动过程的试验条件可知，输入气压恒定，因此可分析多次反复制动过程中制动器温度与上述三者之间的关系。

台架试验中分别采集了制动鼓内表面、外表面、衬片表面和背筋板面的温度，通过对制动器满载、车速60 km/h情况下4个位置的温升情况分析，可以看出制动鼓内表面温度的变化最显著，鼓外表面温度次之，制动蹄背钢板面的温度变化灵敏度最低。此次研究以制动鼓内表面温升为主要研究对象。制动器4个不同位置温度变化情况如图3所示。

图3 制动器4个不同位置温度变化情况(满载，车速60 km/h)

2.1 车辆载荷

由图4制动鼓内表面温度与载荷的关系曲线可以看出：当行驶速度一定时，由于车辆载荷的增加，其存储的动能更多，车辆制动过程中转换的热能越多。所以，在制动距离和行驶速度不变的情况下，制动鼓内表面的温度随载荷的增加而上升。

图4 制动鼓内表面温度与载荷的关系曲线(制动距离1 500 m)

2.2 行驶车速

由图5制动鼓内表面温度与车速的关系曲线可以看出：当载荷一定时，由于车速的增加，初始状态具有的动能更大，车辆制动过程中由动能转换的热能也更多。所以，在载荷和制动距离一定的前提下，制动鼓内表面的温度随速度的升高而增加。

2.3 制动距离

由图6制动鼓内表面温度与制动距离的关系曲线可以看出：当载荷和车速一定时，由于制动距离的改变导致制动次数增加，制动鼓内表面与衬片的摩擦时间变长，其表面温度随制动距离的增加而上升。

图5 制动鼓内表面温度与车速的关系曲线(制动距离1 500 m)

图6 制动鼓内表面温度与制动距离的关系曲线(超载)

3 建立制动鼓升温模型

经过上述的数据处理和分析，发现制动鼓内表面温度与车辆载荷、行驶速度和制动距离都存在一定的关系。利用试验台架采集的大量试验数据，采用统计数多元线性回归方法，在SSPS软件上采用逐步筛选策略进行分析。设制动鼓内表面温度T(单位℃)、车辆轴荷G(单位t)、行驶速度v(单位m/s)、制动距离S(单位m)，则模拟长下坡制动鼓温度的数学模型可以设置为

T=b0+b1G+b2v+b3S

式中：G、v、S为自变量；T为因变量；b0为截距，即常量；b1、b2、b3为回归系数。

将制动距离S、行驶速度v以及车辆轴荷G依次引入模型，当每次引入1个变量后都进行F检验，并对模型内的变量逐个进行t检验，如果当原来引入的变量由于后面变量的引入变得不再显著时，则将其删除，这是一个反复的过程，直到既没有显著的变量选入回归方程，也没有不显著的变量从回归方程中剔除为止[6]。输入和移除的变量如表4所示，其中因变量是温度。

表4 输入/移除的变量

回归方程中复相关系数R为0.969，决定系数R2为0.940，调整决定系数R2为0.938，标准估计的误差为33.333。R2越接近1，所反映的两个变量的共变量比例越高，模型和数据的拟合程度越好。R2=0.940，表示整个回归方程能够解释制动鼓内表面温度的94.0%。模型汇总如表5所示，其中因变量是温度。

表5 模型汇总

注：a.预测变量：(常量)，距离；b.预测变量：(常量)，距离, 速度；c.预测变量：(常量)，距离, 速度, 载荷。

方差分析表显示出各模型中对多个自变量的总体检验， Sig值为0.000，即完全有把握认为回归方程是有用的；F值为601.146，查F分布表得F0.05(3,116)=2.68，即F>F0.05(3,116)，即可判定回归方程中的各个自变量联合起来对因变量有显著影响。方差分析表如表6所示，其中因变量是温度。

表6 方差分析表

注：a.预测变量：(常量)，距离；b.预测变量：(常量)，距离, 速度；c.预测变量：(常量)，距离, 速度, 载荷。

系数表罗列出常量、非标准化回归系数、标准化回归系数、回归系数检验的t统计量观测值和响应的概率值。根据模型建立的多元线性回归方程为

y=-92.547+5.215x1+14.926x2+0.086x3

方程中的常数项为-92.547，回归系数b1为5.215，b2为14.926，b3为0.086，经t检验，显著性概率P值均为0.000，按照显著性水平为0.05的情况下，即可判定回归方程中的各个自变量都对因变量有显著影响。系数表如表7所示，其中因变量是温度。

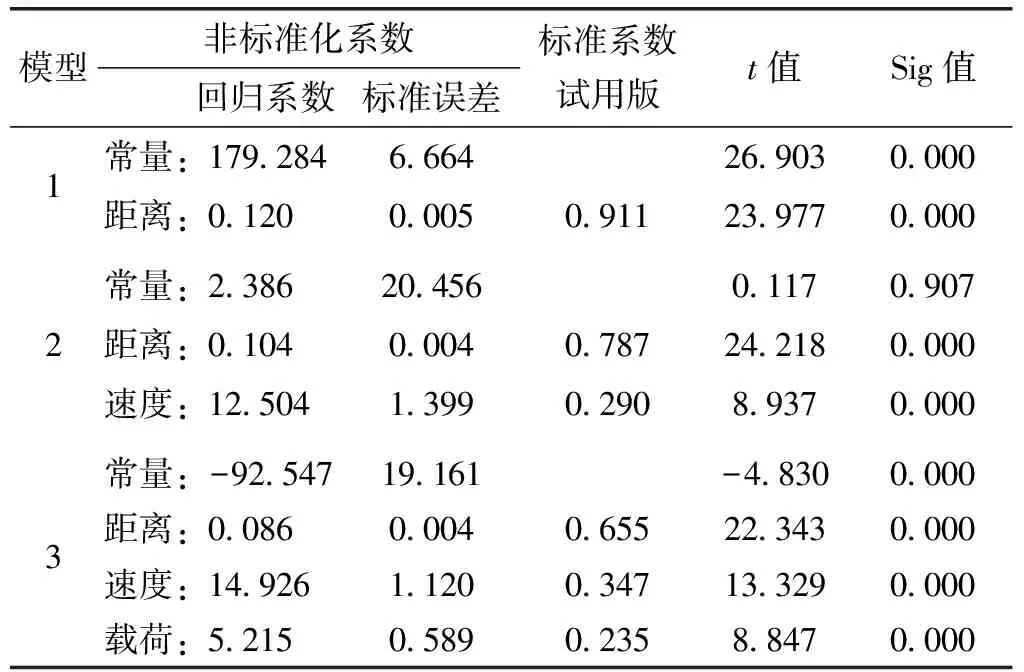
表7 系数表

综上所述，回归分析得到的回归方程为

T=-92.547+5.215G+14.926v+0.086S

式中：T为制动鼓内表面温度，℃；G为车辆轴荷，t；v为行驶车速，m/s；S为制动距离，m。

4 结论

此次研究通过台架试验的方式模拟了重型商用车长下坡持续制动的工作过程，设计了一套完整的试验方法并采集了大量试验数据，分析出制动鼓内表面温度与载荷、车速和制动距离的关系；运用统计学中多元线性回归的方法，利用SPSS软件建立了制动鼓内表面温度与上述三者的预测模型。预测的温升模型为实车制动路试以及整车制动系统的匹配提供参考。