框架顶底板结构对比计算分析
樊长刚
(1.西南交通大学土木工程学院,四川 成都610031;2.中国市政工程西南设计研究总院有限公司,四川 成都 610081)
0 引言
城市中重要的交叉路口常采用立交方式解决交通拥堵的问题,主交通流方向采用跨线高架桥或下穿隧道。由于修建高架桥会带来道路景观、行车视线、汽车噪声的问题,影响周边地块的商业价值和居住环境,现越来越多的平交路口改造采用下穿隧道的方式。
明挖下穿隧道闭口段常采用单箱多室框架结构形式。常规单箱多室框架结构大多采用平面杆系计算方式进行结构模拟分析。由于平面杆系计算方法的局限性,特别是中墙、边墙忽略厚度对框架顶、底板的内力削峰的影响,设计中对框架顶、底板在竖墙处计算结果取值偏大,框架顶、底板在竖墙处配筋量大幅度增加,造成工程材料的浪费及工程投资的增加。下面以双向4车道的单箱双室矩形框架为例,分别采用平面杆系模型和实体单元模型进行对比分析计算,对框架顶、底板跨中和竖墙处内力数值进行对比,并确定其合理取值[1-4]。
1 框架断面
框架结构断面见图1所示。
框架为单箱双室断面,单室净高5.5 m,净跨9 m,顶板厚度0.7 m,底板厚度0.8 m,侧墙厚度0.7 m,中墙厚度0.5 m。顶板覆土等厚,厚度为2.5 m。

图1 框架结构断面图
设计汽车荷载:城-A级;顶覆土平均容重21 kN/m3;侧墙回填土内摩擦角30°;整体升降温10°;地下水位于顶板顶处;基底持力层为稍密卵石层,竖向基床系数25 000 kN/m3;侧墙两侧砂卵石回填,考虑水平弹性约束时,水平基床系数15 000 kN/m3。
2 计算模型
图2为框架结构计算简图。
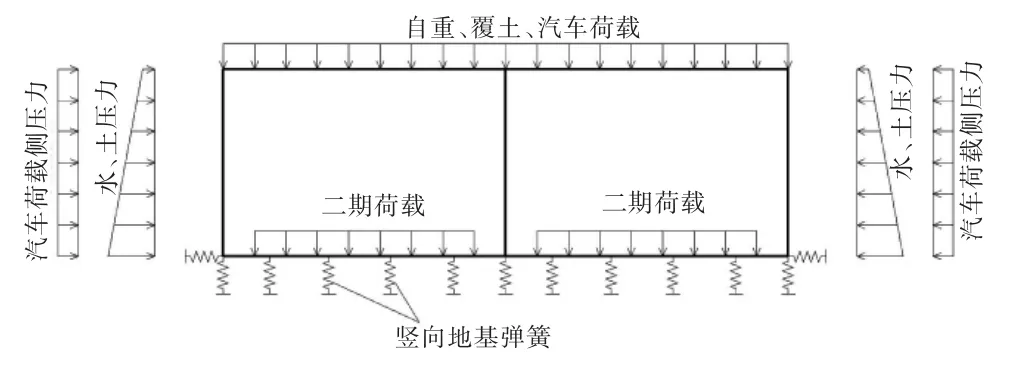
图2 框架结构计算简图
模型一采用平面杆系计算模型,框架结构各部位按构件中线离散单元建模(见图3)。

图3 模型一:平面杆系离散图
模型二采用实体单元计算模型,框架结构各部位按构件实际尺寸建模(见图4)。

图4 模型二:实体单元离散图
两种计算模型外部荷载及约束情况均相同,计算软件均采用MIDAS civil。
3 计算结果
3.1 标准荷载组合工况应力分布(见图5、图6)
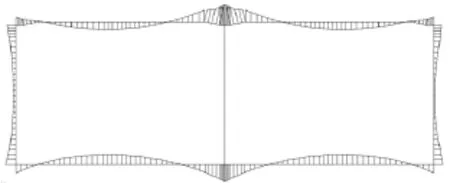
图5 模型一:框架结构轴向应力图

图6 模型二:框架结构SIG-xx方向弥散应力图
从上面两个模型顶、底板轴向应力分布图可以看出,采用平面杆系模型计算的顶、底板在竖墙处均有轴向应力集中的峰值出现,而采用实体单元模型计算的顶、底板在竖墙处,以及临近竖墙的单元应力则相对平均,未出现轴向应力集中的峰值。其原因是平面杆系模型未考虑竖墙对顶、底板有效支承宽度内的应力和弯矩的削峰折减的影响效应,造成竖墙处顶、底板应力集中的情况出现。
3.2 不同荷载工况内力统计
两种计算模型分别对恒载(结构自重+顶板填土+二期铺装+土压力)工况、+水压力工况、顶板汽车工况等三种对结构受力影响较大的荷载工况进行对比分析。
此类下穿隧道框架结构都设计有外防水体系及其保护层(聚乙烯泡沫板、砖砌墙等),或采用支护桩结构对基坑开挖作临时支护,以致水平向水、土压力不能完全有效地作用于侧墙,甚至水平向水、土压力无法作用于侧墙的情况也常出现。基于此,多数设计单位对顶板和底板设计验算时,都不考虑顶、底板轴力的有利影响,偏安全地采用纯弯构件进行设计验算。表1仅统计顶、底板在各主要荷载工况下的弯矩和剪力,忽略轴力的有利影响。
从表1中的内力数据综合分析可得出如下结论:
(1)平面杆系模型计算的顶、底板在竖墙中线处弯矩存在峰值情况;
(2)同一断面实体单元模型计算所得弯矩(绝对值)较平面杆系模型略小;
(3)同一断面实体单元模型计算所得剪力(绝对值)较平面杆系模型略小。
4 竖墙处顶、底板弯矩取值
框架顶、底板在竖墙处弯矩取值设计中常采用弯矩峰值折减或取竖墙边缘对应顶、底板截面弯矩值的两种方式。
(1)框架顶、底板在竖墙处弯矩峰值考虑竖墙厚度对弯矩折减的影响,弯矩折减计算可参照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)4.2.4条要求执行,但折减后的弯矩不得小于未经折减弯矩的0.9倍。

表1 两种模型内力计算对比表
(2)取竖墙边缘对应顶、底板截面弯矩值,同时考虑该截面腋角对板加厚的影响,承托内板结构计算高度可参照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)4.1.6条要求执行。
下面就这两种方式弯矩取值与实体单元模型弯矩值进行对比,以确定其合理取值(见表2)。
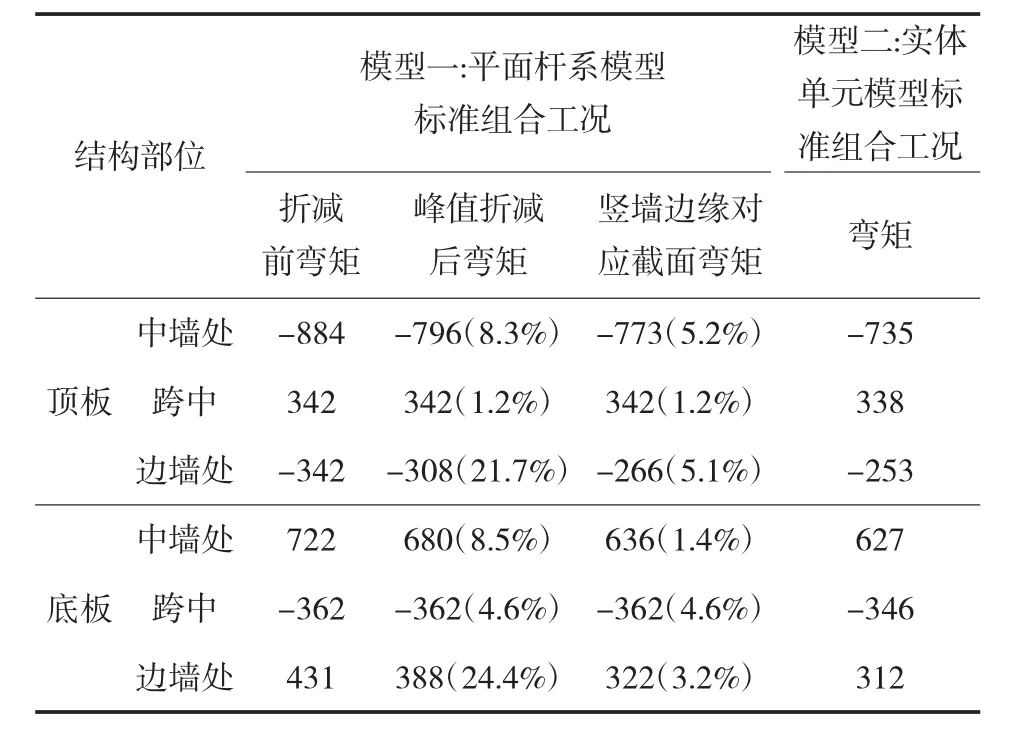
表2 两种计算方法弯矩值对比表(括号内数值为与实体模型弯矩差值百分比)
竖墙处顶、底板有效弯矩取值从表2弯矩值对比可以看出,采用峰值折减后弯矩(绝对值)较实体单元模型对应弯矩(绝对值)大得较多,竖墙边缘对应截面弯矩(绝对值)较实体单元模型对应弯矩(绝对值)略大,其值更为接近。
顶、底板在竖墙处采用峰值折减后弯矩值进行配筋验算虽能够满足设计和使用要求,但笔者认为该种方法弯矩取值与实体模型比较仍然偏大,会导致结构配筋量加大,造成工程材料的一定程度的浪费及工程投资的增加。
顶、底板在竖墙处采用竖墙边缘对应的截面弯矩值与框架结构真实弯矩更为接近,同时也能预留一定的安全度(弯矩偏大1.2%~5.2%),笔者认为该种方法既能保证结构安全,也能相应减少结构配筋量,使结构更加经济合理。
5 结论
钢筋混凝土矩形框架采用平面杆系计算方式进行结构模拟分析,具有建模便捷的优点,模型能取得较好的安全度,文中对框架顶、底板竖墙处弯矩计算及其合理取值作了定量分析,对类似框架结构的计算和合理取值提供借鉴和参考。现有如下几点总结:
(1)平面杆系模型计算所得顶、底板弯矩较实际情况偏大,结构验算是偏安全的。
(2)平面杆系模型计算所得顶、底板在竖墙处弯矩存在峰值情况,设计中可对峰值进行折减处理,折减方式建议直接取用侧墙边缘对应顶、底板截面的弯矩作为结构配筋和验算的内力。
(3)竖墙与顶、底板连接处有条件的应设置腋角,腋角坡比采用1∶3,腋角能有效加大计算截面高度,优化内力,减少结构配筋量。
(4)平面杆系模型计算所得顶、底板剪力较实际情况略小(最多约小8%),设计时应注意抗剪强度的验算,预留一定的抗剪强度的安全系数。
(5)顶、底板结构抗弯和抗剪建议按纯弯构件设计和验算,顶、底板轴力作为其抗弯和抗剪设计的安全储备。

