新型全Heusler合金Cu2WAl的第一性原理研究

严理国，刘惠发，王雨轩，温玉锋,2，伍冬兰



新型全Heusler合金Cu2WAl的第一性原理研究

严理国1，刘惠发1，王雨轩1，*温玉锋1,2，伍冬兰1

(1. 井冈山大学数理学院，江西，吉安 343009；2. 上海交通大学材料科学与工程学院，上海，200240)

采用基于密度泛函理论的第一性原理计算方法研究了新型全Heusler合金Cu2WAl的结构和弹性性能。结果表明：在无磁与铁磁性两种状态下，该全Heusler合金Cu2MnAl型结构的能量低于其Hg2CuTi型结构，其中Cu2MnAl型结构在铁磁态下的能量低于其无磁态；铁磁态下Cu2MnAl型Cu2WAl全Heusler合金的弹性常数不满足Born弹性稳定性准则，从而不能以稳态形式存在。

Cu2WAl；结构性能；弹性常数；第一性原理计算

0 引言

全Heusler合金最早是由德国工程师Fritz Heusler在研究掺杂Al、In、Sn、Sb和Bi等无磁元素的Cu-Mn基合金的铁磁性时发现并以其姓氏命名的一种高度有序的金属间化合物[1]。该类合金的一般化学表达式为X2YZ，其中X和Y元素是过渡族金属元素，而Z元素则为主族元素，其晶体结构是由4个面心立方亚晶格沿着体对角线四分之一相互穿插而形成的，4个亚晶格的Wyckoff坐标为A (0, 0, 0)、B (0.25, 0.25, 0.25)、C (0.5, 0.5, 0.5)和D (0.75, 0.75, 0.75)。根据全Heusler合金中原子的占位情况[2]，其晶体结构存在Cu2MnAl型和Hg2CuTi型两种不同的类型，其中前者是空间群为FM-3M的L21结构，在该结构中X原子占据A和C两个亚点阵位置，Y原子占据B亚点阵位置，Z原子占据D亚点阵位置；后者是空间群为F-43d的XA结构，在该结构中X原子占据A和B两个亚点阵位置，Y原子占据C亚点阵位置，Z原子占据D 亚点阵位置。

全Heusler合金不仅拥有无数的成员，而且这类材料中蕴藏着半导体、半金属铁磁体、超导体、拓扑绝缘体和形状记忆合金等多种应用功能[2-4]，目前已成为凝聚态物理和材料物理科学领域中的一个研究热点。自从第一个由无磁元素Cu、Mn和Al组成的全Heusler合金Cu2MnAl被发现具有铁磁性以来[1]，关于Cu2基全Heusler合金性能的研究就开始引起了科研工作者们的关注，对其进行了实验和理论研究[5-12]。例如： Michelutti等人[8]从实验上研究了全Heusler合金Cu2MnAl磁性、磁各向异性、磁弹性和弹性常数的热变化；Rai等人[9]和Jalilian[10]应用第一性原理计算方法研究了全Heusler合金Cu2MnAl的电子、磁性、光学和弹性性能；Wen团队[11-12]应用第一性原理计算方法研究了全Heusler合金Cu2MnAl和Cu2MnIn的二阶和三阶弹性常数以及与它们相关的一些性能，如声学性能、非谐性能、不同高压下的结构、弹性和德拜温度等。然而，据我们所知，关于全Heusler合金Cu2WAl的研究至今尚未被报道。因此，在本工作中我们将应用第一性原理计算方法对全Heusler合金Cu2WAl的结构和弹性性能进行研究。

1 计算方法

采用基于密度泛函理论的第一性原理软件包ViennaSimulation Package（VASP）来完成本文的理论计算工作[13-15]，用投影缀加波（Projector augmented wave，PAW）方法描述离子与电子间的相互作用[16-17]，用Perdew-Burke- Ernzerhof （PBE）形式的广义梯度近似（Generalized Gradient Approximation，GGA）方法来描述交换关联泛函[18-19]。计算时，选取平面波的截断能为600 eV，电子自洽循环的能量收敛标准选取为10-6eV。采用Monkhorst-Pack方法来产生布里渊区进行积分的特殊网格点[20]，分别选取晶体学原胞和惯用晶胞的网格点为17 × 17 × 17和9 × 9 × 9。

2 结果与讨论

本文首先对无磁和铁磁状态下Cu2MnAl型和Hg2CuTi型全Heusler合金Cu2WAl在不同晶格常数下的原胞总能进行了优化计算，如图1所示。从该图中能清楚地看到，Cu2MnAl型全Heusler合金Cu2WAl无磁和铁磁态的能量均比其Hg2CuTi型结构无磁和铁磁态的能量要低，说明：该全Heusler合金的Cu2MnAl型结构比其Hg2CuTi型结构在能量上相对更稳定；铁磁态下Cu2MnAl型和Hg2CuTi型全Heusler合金Cu2WAl的能量比无磁态下相应结构的能量要低，说明：该全Heusler合金的铁磁态Cu2MnAl型和Hg2CuTi型结构比相应的无磁态结构在能量上相对更稳定。这些意味着：全Heusler合金Cu2WAl的铁磁态Cu2MnAl型结构在能量上是最稳定的。采用Brich-Murnaghan状态方程，对铁磁态Cu2MnAl型全Heusler合金Cu2WAl能量与体积数据进行拟合，如图2所示，我们得到其在平衡态下晶格常数= 6.0405 Å，体模量= 1.04554 GPa。

图1 无磁和铁磁态下Cu2MnAl型和Hg2CuTi型全Heusler合金Cu2WAl能量(Et)与晶格常数(a)的关系

图2 铁磁态下Cu2MnAl型全Heusler合金Cu2WAl能量(Et)与体积(V)关系的状态方程拟合

为了计算铁磁态Cu2MnAl型全Heusler合金Cu2WAl的三个独立弹性常数11、12和44，我们对其惯用晶胞施加一个等体积的正应变变形和一个等体积的切应变变形，相对应的应变张量分别为：

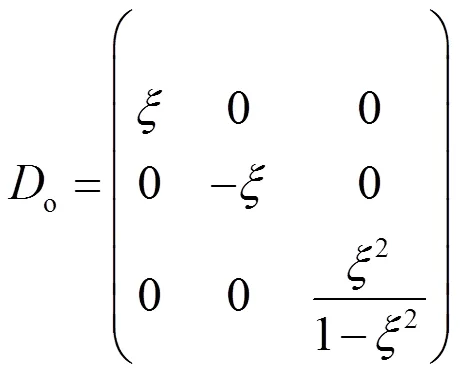
和

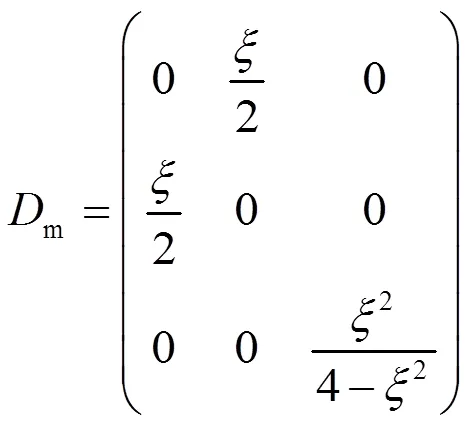
两式中的为应变参数，其取值范围为-0.018到0.018，步长为0.003。两种形变下合金的能量t随应变参数变化关系相对应地分别为：

和

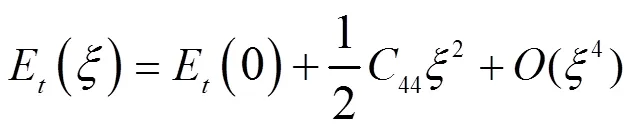
两式中t(0)为平衡态下合金的能量。通过计算出不同应变参数下形变晶胞的能量。根据公式(3)和(4)，采用二阶多项式拟合能量与应变关系，如图3所示，可直接确定弹性常数(11‒12)和44，相应的计算结果分别为-10.04 GPa和64.71 GPa。根据Born弹性稳定性准则[21]，当立方结构晶体的弹性常数同时满足：

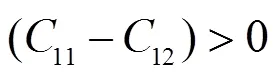
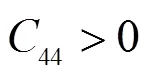
则立方结构晶体可以存在。由于铁磁态Cu2MnAl型全Heusler合金Cu2WAl的体模量和弹性常数44均为正值，而剪切弹性常数(11–12)却具有一个负值，从而不满足Born弹性稳定性准则，所以其不能以稳态形式存在。

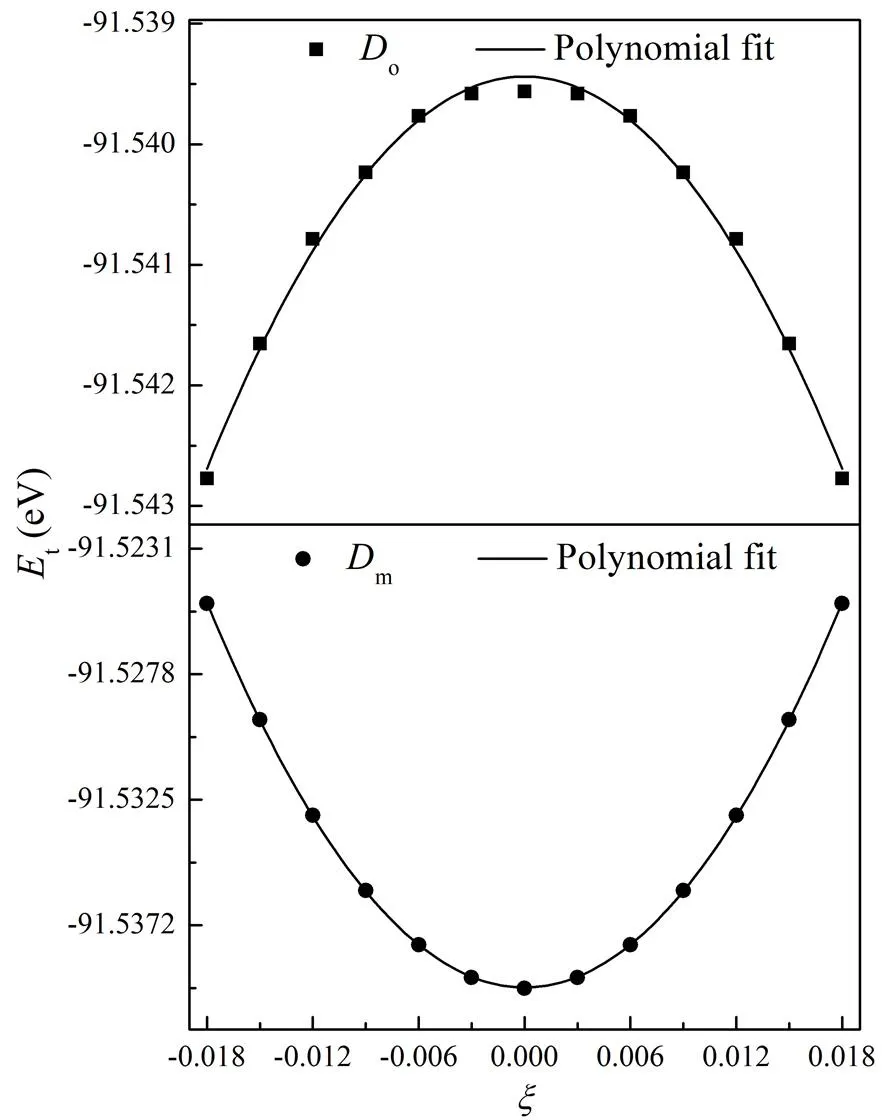
图3 铁磁态下Cu2MnAl型全Heusler合金Cu2WAl能量(Et)与应变参数(ξ)关系的二阶多项式拟合

3 结 论

本文对新型全Heusler合金Cu2WAl的结构和弹性性能进行了第一性原理计算，可以得出如下结论：

1）在无磁与铁磁性两种状态下，该全Heusler合金Cu2MnAl型结构的能量低于其Hg2CuTi型结构，其中Cu2MnAl型结构铁磁态下的能量低于其无磁态；

2）铁磁态下Cu2MnAl型Cu2WAl全Heusler合金的弹性常数不满足Born弹性稳定性准则，从而不能以稳态形式存在。

[1] Heusler F. Über magnetische manganlegierungen [J]. Verhandlungen der Deutschen Physikalischen Gesellschaft, 1903(5): 219.

[2] Graf T, Felser C, Parkin S S. Simple rules for the understanding of Heusler compounds [J]. Progress in Solid State Chemistry, 2011(39):1-50.

[3] Graf T, Parking S S P, Felser C. Heusler compounds-a material class with exceptional properties [J]. IEEE Transactins on Magnetics,2011,47(2): 367-373.

[4] Skaftouros S, Ӧzdogan K, gasioglu E, et al. Generalized slater-pauling rule for the inverse Heusler compounds [J]. Physical Review B, 2013(87): 024420.

[5] Kim K, Kwon S J, Kim W T. Characterization of Heusler alloy thin film, Cu2MnAl and Co2MnSi, deposited by co-sputtering method [J]. Physica Status Solidi, 2004 (214): 1557-1560.

[6] Erb D, Nowak G, Westerholt K, et al. Thin films of the Heusler alloys Cu2MnAl and Co2MnSi: recovery of ferromagnetism via solid-state crystallization from the x-ray amorphous state [J]. Journal of Physics D: Applied Physics, 2010(43): 285001-285009.

[7] Geiersbach U, Bergmann A, Westerholt K. Structural, magnetic and magnetotransport properties of thin films of the Heusler alloys Cu2MnAl, Co2MnSi, Co2MnGe and Co2MnSn [J]. Journal of Magnetism and Magnetic Materials, 2002(240):546-549.

[8] Michelutti B, Perrier de la Bathie R, Tremolet de Lacheisserie E, et al. Magnetiztion, magnetocrystalline anisotropy, magnetostriction and elastic constants of the Heusler alloy: Cu2MnAl [J]. Solid State Communications, 1978(25): 163-168.

[9] Rai D P, Thapa R K. Study of electronic, magnetic, optical and elastic properties of Cu2MnAl a gapless full Heusler compound [J]. Journal of Alloys and Compounds, 2014(612): 355-360.

[10] Jalilian J. Comment on ‘Study of electronic, magnetic, optical and elastic properties of Cu2MnAl a gapless full Heusler compound’ [J]. Journal of Alloys and Compounds, 2015(626): 277-279.

[11] Wen Y, Zeng X, Ye Y, et al. First-principles calculations of acoustic and anharmonic properties of ferromagnetic Cu2MnZ (Z = Al and In) Heusler alloys [J], Journal of Superconductivity and Novel Magnetism, 2018(31): 1847-1856.

[12] Liu L, Zeng X, Gou Q, et al. The structural stability and mechanical properties of Cu2MnAl and Cu2MnIn under pressure: first-principles study [J]. Journal of Electronic Materials, 2018, 47(7): 1-13.

[13] Kresse G, Hafner J. Ab initio molecular dynamics for openshell transition metals [J]. Physical Review B, 1993(48): 13115-13118.

[14] Kresse G, Furthűller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set[J]. Computational Material Science, 1996(6): 15-50.

[15] Kresse G, Furthműller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set [J]. Physical Review B, 1996, 54(16): 11169-11186.

[16] Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method [J]. Physical Review B, 1999, 59(3): 1758-1775.

[17] Blőchl P E. Projector augmented-wave method [J]. Physical Review B, 1994, 50(24): 17953-17979.

[18] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple[J]. Physical Review Letters, 1996(77): 3865-3868.

[19] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1997(78): 1396.

[20] Monkhorst H J, Pack J D. Special points for Brillouin-zone integrations [J]. Physical Review B, 1976 13(12): 5188-5192.

[21] Born M, Huang K. Dynamical theory of crystal lattices [M]. Oxford: Clarendon Press, 1954: 141.

First-principles study of a new full-Heusler alloy Cu2WAl

YAN Li-guo1, LIU Hui-fa1, WANG Yu-xuan1,*WEN Yu-feng1,2, WU Dong-lan1

(1. School of Mathematics and Physics, Jinggangshan University, Ji’an, Jiangxi 343009, China; 2. School of Materials Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

The structural and elastic properties of a new full-Heusler alloy Cu2WAl are investigated using the first-principles calculations based on density functional theory. The results show that the energy of the Cu2MnAl-type structure is lower than that of the Hg2CuTi-typefor the full-Heusler alloy in both nonmagnetic and ferromagnetic states, and the ferromagnetic state of the Cu2MnAl-type structure has lower energy than the nonmagnetic state; the elastic constants of the ferromagnetic Cu2MnAl-type Cu2WAl full-Heusler alloy do not satisfyBorn’s criterion of elastic stability, and thus cannotexist as a stable phase.

Full-HeuslerCu2WAl; structural property; elastic constants; First-principles calculations

1674-8085(2019)01-0009-04

O731

A

10.3969/j.issn.1674-8085.2019.01.003

2018-11-01；

2018-12-08

严理国(1995-)，男，江西赣州人，井冈山大学数理学院本科生(E-mail: jgsuylg@sina.com);

刘惠发(1995-)，男，江西赣州人，井冈山大学数理学院本科生(E-mail: 18379695179@163.com);

王雨轩(1995-)，男，江西九江人，井冈山大学数理学院本科生(E-mail: 13870293115@163.com);

*温玉锋(1977-)，男，江西吉安人，讲师，博士，主要从事计算物理与计算材料学研究(E-mail: jgsuwyf@sina.com);

伍冬兰(1978-)，女，江西吉安人，教授，博士，主要从事分子结构与光谱研究(E-mail: wudonglan1216@sina.com).