用磨粒叶序排布砂轮磨削外圆生成的凹坑表面仿真*
车东泽, 吕玉山, 陈天宇, 熊 伟, 李兴山
(沈阳理工大学 机械工程学院, 沈阳110159)
结构化表面的减摩、减阻、抗黏附是流体动力学领域重要的研究方向,涉及航空、舰艇、汽车、管路运输、风力发电等多个领域[1]。结构化表面制造技术的发展是实现其表面形貌可控的关键,也决定了该技术能否在流体动力学领域成功地应用。
目前,结构化表面的制造方法有多种,如滚压法、超声加工法、激光法、切削法、磨削法等[2],其中磨削法是难加工材料、脆性材料实现大区域结构化表面制造的有效方法之一。对此,国内外学者做了很多研究。谢晋等[3-5]应用数控修整V形尖端金刚石砂轮,磨削单晶硅和石英基板,加工出圆弧半径为22~24 μm的凹坑表面。CHEN等[6]通过修整金刚石成型砂轮,交叉磨削出V形槽结构的光学玻璃表面,其槽宽和深度分别为15 μm和8 μm。ISLAM等[7]和STEPIEN等[8]分别制备了螺旋槽砂轮和双螺旋槽砂轮,用其磨削的工件平面获得了沟槽状非光滑表面。DENKENA等[9-10]制造的成型砂轮在压缩机叶片上磨削出宽度为40 μm、深度为 20μm的结构化筋条表面,并用该叶片做风洞和油槽流体实验,结果表明叶片表面的微沟槽结构有效减少4%的表面摩擦。BRINKSMEIER等[11]通过磨粒矩阵排布,加工出宽度为20 μm、深度为100 μm的沟槽和边长为20 μm的正方形凸台。
这些现有的结构化表面加工方法集中在结构化沟槽表面加工上,而对结构化凹坑表面的加工则存在着很多局限,需要进行进一步的深入研究。本实验提出采用磨粒叶序排布超硬砂轮磨削方法,在外圆表面磨削出结构化凹坑表面,并探索其表面创成机理。
1 磨削加工运动轨迹方程的建立
1.1 叶序排布砂轮的磨粒排布方程
在单层超硬磨料砂轮(电镀砂轮或钎焊砂轮)的设计与制造过程中,依据生物学叶序排布理论,将每个生物组织单元看成是一个磨粒,那么所设计和制造出的砂轮就成为叶序排布超硬磨料砂轮[12],如图1所示。
依据叶序排布理论中的Van.Iterson模型,磨粒在外圆砂轮基体表面的排布位置方程如下:
(1)
其中:Zi、Ri和φi分别为圆柱面中的坐标;i为磨粒在圆柱表面上的叶序序数;λ为叶序发散角,λ取值为137.508°,满足黄金分割率;h为叶序生长系数;rs为砂轮基体半径。
1.2 磨粒轮廓点位置方程
方程(1)揭示的是叶序排布超硬磨料的排布位置,而球体磨粒实际磨削凹坑时的表面轮廓创成,是依靠磨粒垂直于磨削速度方向的截面轮廓为主导完成的。以超硬磨料电镀砂轮为例,如果将磨粒视为半径为rg的球体,在制造过程中有1/2至2/3的磨粒体积被镀层包裹,剩余部分才有可能参与磨削。为了便于仿真,假设磨粒以半球方式参与磨削,因而可在方程(1)的基础上建立半球与磨削速度垂直的最大截面圆上点的方程。
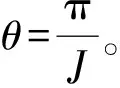
P点坐标:
(2)
Aj点坐标:
(3)
1.3 磨粒磨削运动轨迹方程
图3为磨粒磨削运动坐标示意图。如图3所示:定义工件的固定连接坐标系为Sw(Xw,Yw,Zw),工件的旋转坐标系为Sw′(Xw′,Yw′,Zw′),砂轮的固定连接坐标系为Ss(Xs,Ys,Zs),砂轮的旋转坐标系为Ss′(Xs′,Ys′,Zs′)。设砂轮的磨粒数量为I,加工时间为t,则工件在时间t内相对初始位置的旋转角度为

ωw×t(其中ωw=πnw30,nw为工件转速),砂轮在时间t内相对初始位置的旋转角度为ωs×t(其中ωs=πns30,ns
为砂轮转速),砂轮在时间t内的轴向进给距离为f×t(f为轴向进给速度),砂轮轴线和工件轴线间距离为L(L=rs+rw+2rg-ap,其中rw是工件半径,rg是磨粒半径,ap是磨削深度)。
通过坐标转换可以获得不同坐标系之间的运动关系。转换矩阵Mmn表示从坐标系Sn(Xn,Yn,Zn)到Sm(Xm,Ym,Zm)的坐标转换,进而根据运动关系得到坐标转换矩阵Mww′、Mw′s′以及Ms′s如下:
(4)
(5)
(6)
由方程(3)可得磨粒上某一点在砂轮固连坐标系Ss(Xs,Ys,Zs)下的坐标U=
(7)
设V为t时刻该点在工件固联坐标系Sw(Xw,Yw,Zw)下的齐次坐标,则将U经过(4)~(7)式的坐标变换得到V:
V=[Mww′][Mw′s′][Ms′s]U
(8)
式(8)是磨粒上某一点的运动轨迹方程。
2 实现凹坑表面磨削的运动学条件
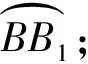
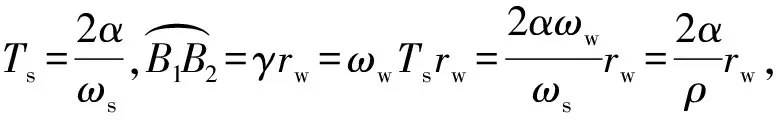
(9)
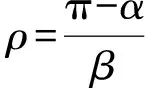
3 结构化表面形貌仿真
3.1 仿真策略与基本条件
图5为磨削加工运动三维仿真流程图。图5中:当输入工件和砂轮的尺寸及加工参数之后,仿真系统将创建工件和砂轮几何实体,获得砂轮磨粒相对于工件固定坐标系的运动轨迹并创成工件表面,获得加工后工件凹坑尺寸,完成仿真。
采用平均磨粒高度来仿真,即取各个磨粒半径的平均值进行仿真。仿真时,一方面确定叶序排布下实现不同结构化表面的条件,即排布与磨削用量的关系,使之能适合各种表面条件;另一方面是对磨料形状和尺寸进行分选,再电镀制造具有一致大小和等高性磨料的砂轮。
仿真过程中设置固定参数为:砂轮半径rs为62.5 mm,工件半径rw为30 mm,砂轮转速ns为1000 r/min;采用粒度代号40/50的CBN超硬磨粒,磨粒平均半径rg为0.175 mm。且文中所有的仿真图长度数据是X向数据,宽度数据是Z向数据,深度数据则通过仿真图右边条的颜色深浅来表达。
3.2 仿真结果与分析
(1)转速比的影响
图6、图7分别是在设定叶序系数h=0.175 mm、磨削深度ap=0.15 mm、保持其他参数不变时,通过仿真程序获得的加工后凹坑与沟槽的边界条件验算图和转速比ρ对凹坑形貌及排布的影响图。由图6可知:ρ=75时,凹坑间还有间距(图6a);ρ=76时,凹坑间没有间距,形成了沟槽(图6b)。而根据公式(9)可计算出产生沟槽的临界值ρmin=76,与图6b的值一致。因此,验证了公式(9)的准确性。
由图7可以看出:工件表面的结构化凹坑是沿工件圆周方向的椭圆状凹坑,且凹坑等间距分布,凹坑最大深度为30 μm;ρ=40时,凹坑长度为2.89 mm;ρ=50时,凹坑长度为2.73 mm;ρ=60时,凹坑长度为2.57 mm。随着转速比ρ增大,凹坑间距逐渐减小,排布逐渐密集,而且在轴向相邻两列凹坑间出现了首尾相互贯通现象。
(2)叶序系数的影响
图8是在转速比ρ=50、磨削深度ap=30 μm、保持其他参数不变时,通过仿真程序获得的叶序系数对凹坑形貌及排布的影响。从图8可以发现:当叶序系数h=0.100 mm时,凹坑在轴向相互干涉,在凹坑边缘隆起形成尖端;当叶序系数h=0.175 mm时,凹坑轴向间距增大,形成各个独立的凹坑;当h=0.400 mm时,凹坑在轴向间距拉开,形成稀疏的凹坑排列。
(3)磨削深度的影响
图9为当转速比ρ=50,叶序系数h=0.175 mm,磨削深度ap对工件表面凹坑形貌及排布的影响。从图8可以看出:当ap=10 μm时,凹坑最大宽度为120 μm,最大深度为10 μm;当ap=30 μm时,凹坑最大宽度为200 μm,最大深度为30 μm;当ap=50 μm时,凹坑最大宽度为250 μm,最大深度为50 μm,此时由于凹坑尺寸加大,使得相邻轴向凹坑出现了重叠效应。
4 结构化凹坑表面的实验验证
使用3.1中仿真过程设置的固定参数进行磨削实验,对加工后的工件进行数据采样及处理,获得图10~图13。其中,图10为叶序排布砂轮加工出的典型凹坑表面,凹坑呈叶序规律排布。
不同转速比下的工件表面形貌如图11所示。从图11中可以看出:当转速比ρ=60时,工件表面的凹坑呈叶序排布,凹坑间距较小,为0.689 mm,排布较为密集;当转速比ρ=50时,工件表面的凹坑分布较ρ=60时的稀疏,凹坑间距为1.807 mm;当转速比ρ=40时,工件表面的凹坑分布最为稀疏,凹坑间距为2.219 mm,三者中最大。由此可知,工件表面凹坑的周向间距随着ρ的增大而减小,这与图7的结果一致。

(a)ρ=40(b)ρ=50(c)ρ=60图11 不同转速比下的工件表面形貌Fig. 11 Surface morphologies of workpiece at different speed ratios
图12为不同磨削深度下单个凹坑的截面尺寸测量图。由图12可知:当ap=10 μm时,凹坑宽度(Z)为115 μm,最大深度(Y)约为10.5 μm,毛刺隆起高度约为4.5 μm;当ap=30 μm时,凹坑宽度为210 μm,最大深度约为31.6 μm,毛刺隆起高度约为13.8 μm;当ap=50 μm时,凹坑宽度为303 μm,最大深度约为53.8 μm,毛刺隆起高度约为26.3 μm。凹坑的宽度与深度随ap的变化趋势与图9一致,且毛刺隆起高度均为其磨削深度的一半。
不同叶序系数下的工件表面形貌如图13所示。图13中:当h=0.100 mm时,凹坑轴向排布密集,相邻两排凹坑轴向间距最小为0.100 mm;当h=0.175 mm时,凹坑轴向排布比h=0.100 mm时稀疏,周向间距没有明显变化,相邻两排凹坑轴向间距最小为0.175 mm;当h=0.400 mm时,凹坑轴向间距明显大于前两者,而周向间距依然没有变化。凹坑的轴向间距变化趋势与图8一致。
5 结论
提出了应用磨粒叶序排布砂轮磨削外圆产生结构化凹坑表面的方法,构建了砂轮模型并结合坐标变换获得了磨粒的运动轨迹〗方程,再控制加工时间模拟出磨粒的动态加工过程,实现了磨削加工材料去除的仿真,获得了结构化的凹坑表面,并通过对比获得了砂轮不同排布参数及加工参数对仿真结果的影响规律。
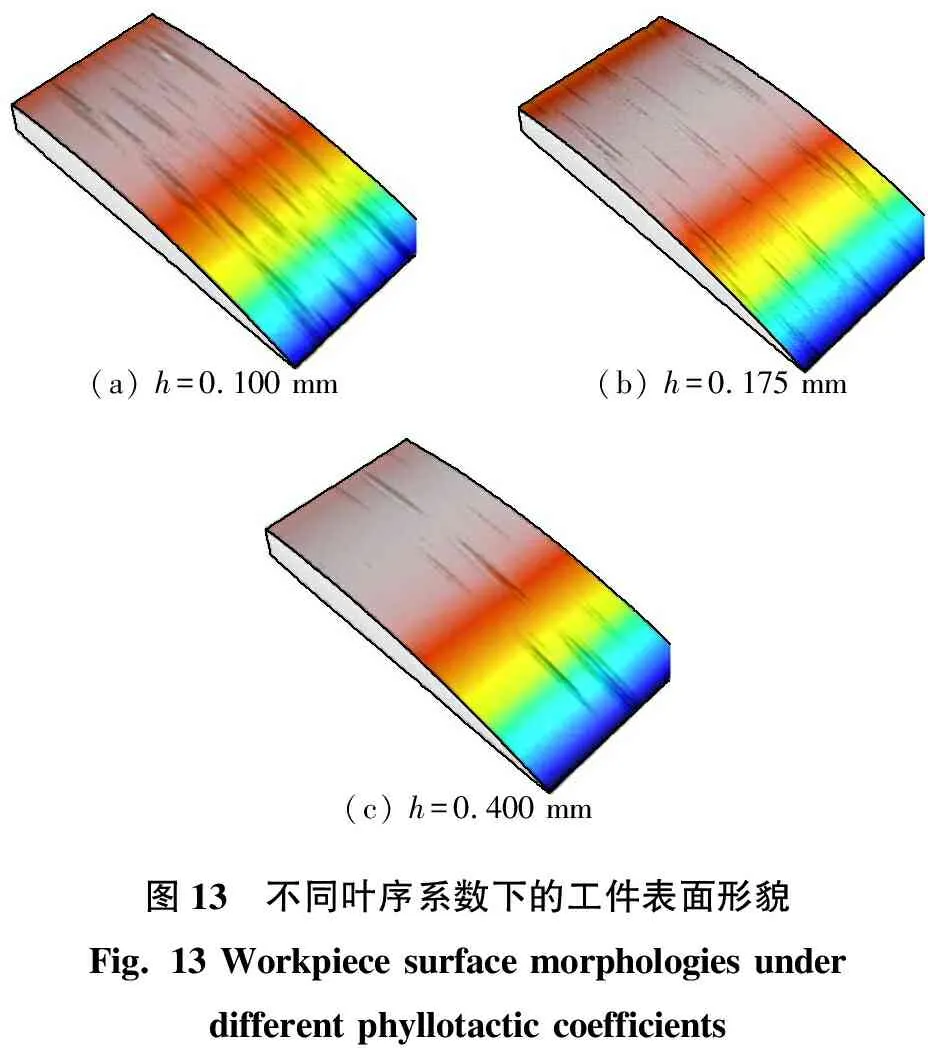
(a) h=0.100 mm(b) h=0.175 mm(c) h=0.400 mm图13 不同叶序系数下的工件表面形貌Fig. 13 Workpiece surface morphologies under different phyllotactic coefficients
磨削实验验证了该方法的可行性与仿真的正确性。仿真及实验结果表明:转速比越高,凹坑径向排布越密集,凹坑尺寸越小;叶序系数越小,凹坑轴向排布越密集;磨削深度越深,凹坑宽度与深度越大,且毛刺隆起高度越高,约为磨削深度的一半。

