基于禁忌搜索算法的自动化集装箱码头船舶配载研究
俞 宙,许冬敏,张 琼,丁 一,林丹萍
(1.上海冠东国际集装箱码头有限公司,上海 201306;2.上海外国语大学 贤达经济人文学院,上海 201306;3.上海海事大学 物流研究中心,上海 201306;4.上海海事大学 物流工程学院,上海 201306)
引 言
船舶大型化和港口作业智能化趋势下,集装箱码头对船舶的装卸作业效率提出了高难度要求。因此,如何有效地提高码头运作效率,缩短船舶在港作业时间便成了集装箱码头亟待解决的问题。在新形势下,传统码头的运作模式已经难以适应未来趋势的发展,世界大港均通过建造自动化码头解决该难题。
自动化集装箱码头通过对作业计划的优化的做法,解决作业过程中堆场冲突、岸桥作业效率低下等问题。码头通过将生产运营“事中控制”向“事前计划”的转变,极大地提高码头运营效率,使各项生产要素得到更加合理的配置。自动化码头作业计划的核心问题包括:岸桥调度计划、船舶配载计划以及堆场作业计划。本文将对船舶的自动配载问题进行研究。
船舶配载计划是一个NP-Hard问题[1],现有的文献主要有船舶的预配计划与码头的实配计划研究。关于实配计划的研究,Imai等(2006)[2]运用加权法对所建立的多目标配载整数规划模型进行求解,并得到近似优解。Ambrosino(2006)[3]提出了一个基于三个层次的分层算法,以船舶的总装载时间最短为目标,考虑重量、箱型尺寸、稳性等约束条件,选用热那亚港的数据进行算例分析。Sciomachen等(2006)[4]运用三维装箱方法,以装船总时间和桥吊利用率为优化目标,考虑集装箱和船舶的结构、作业约束,提出了一种优化建模方法。Ambrosino等(2009)[5]以最小化总装载时间为目标,以船舶重量分布、箱型尺寸和稳性为约束,提出了一个三阶段算法。首先将整船按区分配在场箱,以缩小搜索空间。其次建立各区装载计划的整数规划模型。最后将局部搜索交换策略算法结合。Álvarez等(2006)[6]充分考虑了翻箱作业、正面吊运输、以及船上重量原则,应用禁忌搜索算法研究了码头以正面吊为装卸设备的集装箱船舶配载问题。Lee等(2009)[7]在研究配载问题前,对集装箱堆场布局进行优化,运用整数规划模型以及分支算法来对集装箱堆场的布置问题进行求解。Ambrosino等(2010)[8]针对配载问题提出禁忌搜索算法的设计理念,并用启发式和蚁群优化算法求解问题。杨杰敏等(2011)[9]研究了基于多项作业原则的配载优化问题,提出了3层规划模型,重点研究堆场取箱作业,充分考虑重量原则、作业冲突原则,建立数学模型,采用分支定界进行求解。Delgado等(2012)[10]将配载问题分解为两个阶段,第一阶段为主贝计划,为集装箱分配贝块;第二阶段为船槽分配阶段,为贝块中的集装箱分配具体的箱位。Monaco等(2014)[11]研究了堆场装卸设备为跨运车的集装箱船舶实配问题,提出用两步启发式算法进行模型求解。何钢等(2015)[12]构建了贝内配载问题的数学模型,设计了一种改进的混合遗传算法,融入A*算法的启发式搜索思想。并以某自动化码头为研究实例,对贝内配载问题进行求解。Francisco Parreño等[13]研究了班轮船舶配载问题,提出了新的整数规划模型和贪婪随机自适应搜索算法,该方法能够在1 s之内找到高效方案。
在集装箱船舶配载研究方面,现有的研究文献从码头角度对集装箱装船实配问题的研究甚少。同时,国内外学者对配载问题的研究重点大多集中在集装箱与船箱位的位置对应关系,综合考虑堆场作业冲突和作业过程中的翻箱等因素较少。因此,本文将从船舶配载作业均衡角度出发,对自动化集装箱码头的配载优化问题展开研究工作。
1 问题描述
集装箱实配是码头装船作业的重要一环,是在需要装船的集装箱及其堆场位置已知的前提下,符合船方预配要求的同时综合考虑堆场工艺、装卸设备及翻箱等因素,寻求最优的配载决策,为堆场带装船集装箱分配合理的船舶位置。装船开工前,码头需制作配载计划。配载计划就是在预配船图确定后,根据船舱箱位的配载规则进行实配的方案,由配载图形式表示。
实配是带复杂约束的多目标优化问题。制定配载计划的已知信息包括船公司预配船图、船舶现有积载信息、待装船集装箱信息以及码头设备资源状况与装卸工艺。码头制定配载计划的核心是保证满足泊位策划制定的船期要求,尽可能保证桥吊作业计划按原有时间开展,保证桥吊的连续作业。同时,减少堆场出箱冲突,并降低堆场装船翻箱率,使配载图既满足船舶稳性、强度等船方要求,又满足码头组织生产的效率要求,使得总的装船速度最快。
通过对自动化集装箱码头实际状况的综合考量,其制定配载计划的决策目标主要包括最小化堆场翻箱量、最小化水平运输距离及均衡堆场箱区间作业量。配载计划需要同时满足船方和码头的要求,在保证船舶适航性的同时提高作业效率。其制定需遵循满足预配要求与码头实际作业要求原则。预配图给出了船箱位预配位置要求和船舶结构等信息,要求配载保证船舶稳性、满足船体强度要求、保证船舶吃水差及避免倒箱作业。同时需符合码头堆场取箱规则、符合码头单船作业计划要求、尽可能保证作业路顺利作业。
2 模型建立
2.1 模型假设
假定以下条件已知:
1)集装箱船舶的结构和船箱位信息;
2)待配载集装箱的信息(堆场位置、箱型、重量等级、箱号、目的港等);
3)预配船图信息;
4)桥吊开路计划与作业计划。
为便于建模,同时考虑问题求解的实现条件,做出以下合理假设:
1)港口机械设备配置合理,有足够的码头作业机械保证配载效率不受影响,且无需考虑作业过程中机械设备的故障或维修情况;
2)待配出口箱数量不超过计划可装载的船箱位数量;
3)危险品箱、冷藏箱等特殊箱在船上的配载位置已设定,且不考虑垫脚箱;
4)不考虑不同箱型集装箱作业工艺的不同且假定作业时间相同;
5)预配中已考虑船舶稳定性等指标。
2.2 参数定义
1)定义集合
N—堆场内所有待配集装箱的集合,

P—船箱位的集合,p∈P,p≡ (x,r,y);
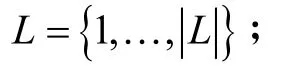
Ψ(l)—属于船栈l的船箱位集合,ψ(l) ⊂P;
D—配载中涉及的船舱的集合,D= { 1 ,…d};
Ω(d)—属于船舱d的船箱位集合,Ω(d) ⊆P;
cp—预配中规定船箱位p可放置的集装箱属性(包含卸货港、箱尺寸、箱型、空箱或重箱);
N(p)—可配载到船箱位p上的集装箱的集合,其中ci=cp;
P(i)—可配载集装箱i的船箱位的集合,其中ci=cp;
Δ(i)—同集装箱i位于堆场同一场栈,且所处位置在集装箱i上方的集装箱集合,Δ(i)⊂N;
B—堆场箱区的集合;
T—时间段的集合,时间段由t(第t小时)表示,{1,2 ,. .. ,tmax}。
2)定义参数
rjk—船箱位,r为贝号,j为列号,k为层号;
θp—船箱位p装船作业时间;
τip—将集装箱i从其场箱位配载到船箱位p所需水平运输时间;
Wl—船栈l可承载的重量上限值;
Wd—船舱d可承载的重量上限值;
ⱳi—集装箱i的重量;
π(p)—同船箱位p位于同一船栈且所处位置在船箱位p正上方的船箱位,即若p=(r,j,k),则π(p)=(r,j,k+1);
σ—堆场翻一次箱所需时间;
b—堆场箱区编号;
ubi—在t时间段箱区b的最大预设作业时间;
M—充分大的正数。
2.3 决策变量
xip—0-1变量,当且仅当集装箱i被配载到船箱位p上时为1,否则为0。
zij—0-1变量,当且仅当集装箱i在集装箱j之前配载时为1,否则为0。其中j∈ Δ (i)。
vpbj—第t时间段箱区b完成对应船箱位p配载任务的作业时间。
γbt—在第t时间段箱区b的剩余可作业时间。
功能性成分测定:氨基酸含量和核苷酸含量的测定分别参考文献[7]和[8]的方法;多糖含量和多酚含量的测定分别参考文献[9]和[10]以及[11]和[12]的方法。
γtmin—在第t时间段内所有堆场箱区中最小的剩余可作业时间。
2.4 数学模型
目标函数:

约束条件:

式(2)表示每个集装箱只能被配载到一个船箱位上。
式(3)表示每个船箱位只能配载一个集装箱。
式(4)表示集装箱船上位于同一船栈的集装箱要求轻箱压重箱。
式(6)定义了堆场翻箱。
式(7)表示船舱配载的集装箱重量小于该舱的重量极限。
式(8)保证配载的集装箱类型与船箱位类型一致。
式(9)定义箱区剩余可作业时间γbt。
式(10)表示在某一时间段内所有堆场箱区中的最小剩余可作业时间。
式(11)和(12)定义了相关决策变量为0-1变量。
式(13)表示相关变量的取值范围。
通过上述模型看,船舶配载问题是带复杂约束条件的组合优化问题。由于配载模型的高复杂性、计算量大、搜索速度慢等特点,因而如何提高搜索效率,得到最优解(近似最优解)成为解决配载问题的关键。鉴于禁忌搜索算法作为一种不依赖于问题的高效寻优算法,能有效地解决大型组合优化和整数规划问题,且在集装箱码头生产计划与作业计划方面有着广泛且良好的应用。因此,本文将采用禁忌搜索算法对该配载模型进行求解。
3 算法设计
基于配载模型,本节将设计禁忌搜索算法对自动化集装箱码头船舶配载问题进行求解,通过寻找满意的配载方案,最终得到待配集装箱与船箱位之间的匹配关系。
首先,初始化配载状态,包括堆场待配载集装箱信息、船舶贝位的船箱位信息、迭代次数等已知参数。
3.1 编码方式
本文解决集装箱船舶配载问题的核心在于确定待装船箱在船上的位置,使配载计划方案能够满足船公司和码头方的相关技术和理论要求,因此编码应包含配载位置信息。
由于桥吊作业计划已得到确定,故各作业船贝的作业顺序和作业开始时间也随着得到确定。故每个船箱位都可得到一个预估的作业时间,船箱位配载次序已得到确定。为得到场箱位与船箱位的匹配关系,本文采用1~n的自然数对场箱位进行实数编码,用l代表编码序列。编码的每一位分别代表船箱位,每一位的值代表场箱位。图1展示了n个场箱位的编码序列。

图1 编码序列
图1表示第1位船箱位装载场箱位为3的集装箱,第5位船箱位装载场箱位为n的集装箱。按照上述方法进行编码的任意序列都代表了配载问题的决策结果(配载位置),为后续操作奠定了基础。
3.2 适配值函数的构造
适配值函数用来界定搜索状态的优劣性。本文选用目标函数作为适配值函数,根据本文模型,将适配值函数设计为:
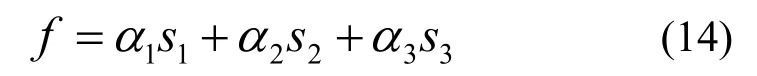
式(14)中:s1,s2,s3为子决策目标,α1,α2,α3是各子决策目标权重系数。权重系数的设立方法遵循适应性权重,即根据当前候选解集的信息进行适应性调整,计算步骤如下:
若最大决策目标不等于最小决策目标:

若最大决策目标等于最小决策目标:
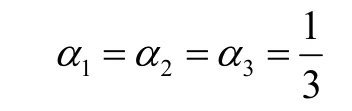
3.3 初始解的获得
由于禁忌搜索算法的性能在较大程度上由初始解的质量决定。因此,本文在配载计划制定的初始阶段,通过在多个随机解中选择翻时间与水平运输时间最短的解作为初始解,以提高算法收敛的速度,提高解的质量。
3.4 邻域移动
对于船舶配载问题,本文通过随机交换两个场箱位编号实现邻域移动,随机交换场箱位编号需满足模型约束条件。具体的操作方式如图2所示。

图2 交叉操作示意
3.5 禁忌表的设置
禁忌表的设置包括禁忌对象与禁忌长度的设置。对于本文所研究的船舶配载问题,根据邻域移动的设计特点,以每次迭代过程进行交换的场箱位编号对为禁忌对象。例如:当图2中场箱位编号8和43进行位置交换时,编号对(8,43)将加入到禁忌表中,设定该编号对在规定迭代次数内不得被再次访问。本文选用固定长度法设定禁忌长度。根据编码步骤可知,若本文的问题规模n=100,则本文的禁忌长度t=10。
3.6 选择策略
对于船舶配载问题,若当新解计算得到的适配值比原解对应的适配值小,则将该新解作为本次迭代的邻域最好解。用公式表示为:

式(15)中:l为当前解,l’为选出的邻域最好解,s(l)为候选解集,为邻域V的一个子集,f′(s(l))为s(l)的适配值函数。
3.7 藐视准则
本文选取基于适配值的藐视准则对优良状态实行解禁,当禁忌候选解适配值优于当前最优解时,则将其从禁忌表中剔除。例如:当交换编码对(8,43)经过多次迭代后,计算得到的适配值大于当前最优值时,即f(s(l))<f(l*),将编码对(8,43)从禁忌表中剔除。
3.8 终止准则
本文通过设置算法最大迭代次数作为终止准则,并从当前代选出代表最佳配载位置的编码序列作为输出。
4 算例分析
4.1 初始数据
为验证本文所提出模型额正确性与有效性,选取艾伯特马士基(ALBE MSK)、航次为632W的集装箱船01舱中的31个集装箱位为配载计划研究对象进行算例分析。算例中,关于船舶 01舱的预配(图3)、船箱位信息(表1)、在场箱信息(表2)均为已知条件。

图3 预配船示意
01舱31个预配船箱位信息如表1所示。主要包括:船箱位、卸货港、尺寸(20 ft、40 ft)、箱型(高箱、平箱)、空箱或重箱;“箱型”一列中,G代表平箱,H代表高箱。“空/重”一列中,F代重箱,E代表空箱。

表1 船箱位信息
需要配载到01舱的31个在场箱信息如表2。

表2 在场箱信息
根据该码头的实际操作情况,设置模型中涉及的参数。其中,由 AGV的平均水平移动速度为v=6 m/min及集装箱所在箱区与船贝之间的距离,可获得配载过程中每个集装箱的水平运输时间τip。假定桥吊每小时可完成 24个动作,处理一个集装箱任务需2.5 min,则根据桥吊作业计划及配载规则可得出每个船箱位的开始装船作业时间θp。堆场翻箱时间σ=3.3 min。式(14)中权重系数设置情况为:α1=0.4,α2=0.3,α3=0.3。对禁忌搜索算法参数设置如下:取迭代次数Tmax=300,禁忌长度H=10,邻域个数U=10。
4.2 结果分析
基于以上数据,在实验环境为Intel(R) Core(TM)i3-2350M CPU@2.30 GHz、内存为4G的个人计算机上,采用MATLAB软件对所提出的禁忌搜索算法进行程序开发工作,求解算例。利用禁忌搜索算法进行计算,对01舱的31个集装箱的配载计划进行求解,通过多次试验,得到最优的配载结果。进而可得出总目标函数值与各个子目标函数值,如表3所示。

表3 目标函数结果
按船贝图的形式图形化展示配载方案。从船贝配载角度看,01舱位的配载结果如图4所示,图中数字编号代表来自不同场箱位的集装箱编号,船箱位与所需装船的集装箱相匹配。

图4 船贝配载结果示意
为了进一步分析模型中堆场箱区间作业时间均衡约束对配载计划的影响,根据配载结果,从堆场配载角度,还可以绘制出01舱位配载结果所对应的堆场箱区发箱点分布图,以了解在配载过程中发箱点聚和散的问题,基于均衡约束进行船舶配载,可以有效分散箱区作业量,减少堆场翻箱时间和水平运输时间。从而避免产生水平运输拥堵和堆场机械作业繁忙,减少作业冲突,也有效缩短了集装箱的装船作业时间。基于堆场发箱点的分布,可预估堆场作业冲突,使得全场船舶作业过程中尽量的减少作业冲突和实现作业冲突的预警。
为检验禁忌搜索算法的收敛性,根据待配载集装箱数量设计5组不同规模的算例,进行多次实验,通过数据统计,得到禁忌搜索算法中目标函数值与迭代次数之间的关系,如图5所示。

图5 目标函数收敛曲线
由图 5 可知,设定Tmax= 3 0 0,随着迭代次数的增加目标函数的值先不断减小,后呈现平稳状态,在迭代达到120次时第一次搜索到最优解。从整个目标函数收敛曲线图可知,随着迭代次数的增加,算法采样规模扩大,估计值逐渐趋于精确,在一定代数后找到较优的解。表明禁忌搜索算法可在指定迭代次数内搜索到最优解,验证了本文所设计的禁忌搜索算法具有可靠性。
综上所述,根据自动化集装箱码头船舶配载模型和设计的禁忌搜索算法,计算结果满足模型中作业约束条件,实现了决策目标,表明所提出的模型和算法是有效并且可靠的。
5 结 论
本文研究了自动化集装箱码头集装箱船舶配载问题。基于自动化集装箱码头的研究背景,首先对实配问题进行抽象,充分考虑作业均衡因素,以最小化翻箱时间、水平运输时间和均衡堆场箱区间作业时间为决策目标,综合考虑预配规定与实配原则,建立了自动化集装箱码头船舶配载的多目标混合整数规划模型。设计基于配载位置的禁忌搜索算法进行求解,并详细阐述了算法的实现步骤。以名为艾伯特马士基的集装箱船舶配载为实例进行算例分析,得到了最优的配载结果,并用图形直观展示了 01舱的配载计划。通过不同规模的算例得出该算法可有效求解自动化集装箱码头船舶配载问题。在集装箱船舶配载计划制定过程中,本文所提出的数学模型以及设计的禁忌搜索算法具有实际借鉴意义。

