基于因子载荷矩阵的复杂气井井筒完整性失效贡献因素重要度量化方法*

刘铭刚

(中国石化青岛安全工程研究院，山东青岛 266071)

0 引言

井筒完整性(Wellbore Integrity,简称WI)[1]评价技术的研究始于1977年BP公司首先建立的油气井完整性管理体系，其于1980年确立了以完井技术为核心的油气井完整性管理方法，提出并阐明了油气井完整性工程师岗位对于油气田开发的重要性。进入21世纪，油气井完整性研究方面走在世界前列的是挪威国家石油公司牵头的挪威石油工业协会。国内的新疆地区油气田和西南地区油气田最早与国际接轨，将油气井完整性的概念开始在国内推广，并进行了卓有成效的探索研究工作。

2010年“深水地平线事件”后，各油气资源大国、油气开发企业和技术服务公司等纷纷吸取教训，开始重视油气井井筒完整性领域的技术开发和科学研究。挪威石油工业协会牵头成立由BP、Conoco Phillips、Eni Norge、Exxon Mobil、Marathon、Nexen Inc.、Norske Shell、Statoil、Total等石油技术服务的龙头企业组成工作团队，负责编写井筒完整性标准《OLF Commended Guidelines for Well Integrity》，到2011年挪威石油工业协会完成对Norsok D-010标准《Well Integrity in Drilling and Well Operations》(Revision 3, Aug.2004)的更新。2011年美国石油学会发布API96《Deepwater Well Design and Construction》，其中对油气井设计和钻井建井中的井筒完整性提出了比较规范的概念和技术条款。2013年挪威石油工业协会对上述两部井筒完整性的主要标准进行了修改和增补，将“油气井井筒完整性”定义为：采用有效的技术、优化的设计及合理的管理模式来降低运行风险，保证油气井在达到废弃前的运行周期内的安全可靠性；API标准将“油气井井筒完整性”定义为：采用技术、操作和管理措施，使得油气井井筒在整个生命周期中保持稳定、正常的流体注入、采出状态[2]。

“井筒完整性”概念的提出为油气井井筒设计和安全评价的综合研究提供了方向，而完整性分析最重要的内容是建立有效的可靠性评价方法。现行的工程结构设计方法多以名义值或最大值作为可靠性评价的依据，如API 5C5、ISO 10400、SY/T5724[3-5]等。但对复杂油气井，如普光气田的超深高温高含硫气井，其井筒结构是由油管、套管、水泥环、地层和胶结面等组成的多层有机整体，该类井筒的完整性无法用某个单一的名义值来评价。目前针对井筒完整性的评价方法[6-11]存在以下问题：或者由于计算模型复杂导致考虑的可靠度指标过少，或者没有考虑参数之间相关性，导致计算变量过多，造成计算过程繁琐复杂。因此本文基于因子分析方法，对影响复杂油气井井筒完整性指标的参数进行分析，推导复杂油气井井筒完整性失效贡献因素的因子分析模型和因子载荷矩阵，以最少信息丢失为目标压缩参数数量，在不简化可靠度计算模型的基础上对井筒失效的贡献因素进行分类和重要度排名，最终通过普光气田试验井的应用验证本文方法的可行性。

1 复杂油气井井筒风险贡献因素因子分析模型

可靠度计算中参数的随机性规律是通过统计变量分析得到的。统计变量数量越多，可靠度计算模型的精度也越高。但是若有大量的变量参与可靠度建模，不仅将增加计算工作量，而且变量之间信息的高度重叠和高度相关也会给概率计算带来许多障碍，图1为变量间相关关系示意图。解决上述现象最直接的方法是压缩参数变量的数量，但这必将引起有效信息丢失，进而导致可靠度计算精度的下降。

图1 变量间相关关系示意

因子分析[12,13]的思想是考虑参数间的相关性，以最少的信息丢失为前提，将大量无序的原始变量压缩成较少几个综合因子的方法，图2为典型因子分析过程。它具有以下性质：有效因子个数远远少于初始变量的数量；有效因子能够反映初始变量的根本特征或主要性质；因子之间的线性关系不显著；因子具有命名解释性。

图2 典型因子分析过程示意

对一般的可靠度计算模型，设Z=(Z1,Z2…Zm)为统计方法得到的具有随机性的变量，因子分析模型可用式(1)表示为

Zj=μj+aj1F1+aj2F2+aj3F3+…+ajmFm+Uj(j=1,2,3…n,n为原始变量总数)

(1)

用矩阵的形式表示为式(2)所示

Z=μ+AF+U

(2)

其中，μ为总体随机变量Z的均值；F为因子，是m个高维空间中互相垂直的坐标轴；A为因子载荷矩阵；aji(j=1,2,3…n,i=1,2,3…m)为因子载荷，是原始变量在第i个因子上的第j个负荷；Zj为第j个变量的标准化分数；Fi(i=1,2…m)为共同因素；m为所有变量共同因素的数目；U为特殊因子，为原有变量不能被因子解释的部分，其均值为0，表示多元线性回归模型中的残差；Uj为变量Zj的唯一因素；aji为因子载荷。

为方便计算，对变量Z进行标准化处理使其均值为零，方差为1，则每一个变量aji都可以表示成公共因子Fi的线性函数与特殊因子Uj之和，即

Z=AF+U

(3)

其中，

上式满足：m为共同因子的数量，Zj为第j个变量的标准化分数；Fi(i=1,2……m)为共同因素，均数为0，方差为1；Uj为变量Zj的唯一因素，均数为0，方差为δj；Fj与Uj相互独立。

具体地，假设变量Zj为m维因子空间中的某个向量，aji表示因子载荷矩阵A中Zj在Fi上的投影，相当于线性回归模型中的标准化系数[14,15]；在因子不相关(即Fi相互独立)的情况下，因子载荷aji反映因子对所解释变量的贡献。若定义因子载荷为不大于1的数，则其绝对值越逼近1，表示变量与因子的相关性越强。因此对井筒完整性相关的统计参数开展因子分析，就是对全部统计变量的因子载荷矩阵求解和排序的过程。

2 因子载荷矩阵和因素贡献度分析

在进行井筒完整性参数的可靠性分析时，须对从测井数据、厂家信息及规范统计的大量参数变量进行随机性分析：油管、套管和水泥环的参数，如壁厚、直径、弹性模量、泊松比、井筒直径等；井筒周围的地层参数，如上覆岩层压力、最大主应力、最小主应力、地应力非均匀系数，地层弹性模量、泊松比；以及生产参数，如环空压力、油管近壁压力、日注采量、生产压差等诸多变量。考虑一般情况，设与井筒完整性相关的所有参数统计变量构成的向量为Z

(4)

其中，n为与井筒可靠性相关的随机参数变量总数。则对(3)式所述的因子模型，变量Zj与因子Fi的协方差Cov(Zj,Fi)为

(5)

根据前面的讨论，当Z为标准化后的井筒完整性参数变量向量时，有

DZj)=1

(6)

D(Fi)=1

(7)

其中，D(Zj)和D(Fi)分别为Zj和Fi的标准差。此时因子载荷aji可由式(5)的变形式(8)求出

(8)

因此因子载荷矩阵A可表示为式(9)的形式

(9)

容易求出矩阵(9)的特征根λi(i=1,2……m)并排序，使满足

λ1≥λ2≥…≥λm≥0

(10)

分别对应单位特征向量为Ti(i=1,2……m)，则从矩阵理论可以证明因子载荷矩阵A表示为

(11)

(12)

3 应用实例

3.1 普光T4井筒完整性失效贡献因素分析

以普光T4井为例，基于本节推导的因子分析模型对造成顶事件“普光T4井筒完整性失效(T)”的贡献因素进行分析。井筒完整性失效贡献因素及代码符号如表1所示，贡献因素的事件逻辑图形式表达如图3所示。

从表1和图3中可以看出，当不考虑油气田生产管理、施工等因素时，已有23类底事件代表的参数对顶事件的发生有直接影响。若按传统的可靠性理论进行可靠性分析，须对底事件分别进行随机性分析、抽样分析和概率分析，工作量十分巨大。为此，本文以井筒结构的失效机理和失效形式作为底事件的基本属性，对上述23类参数进行 因子分析，根据其对井筒失效的贡献程度进行重新分类和重要度打分，从而在信息丢失最少的情况下实现参数数量的压缩。

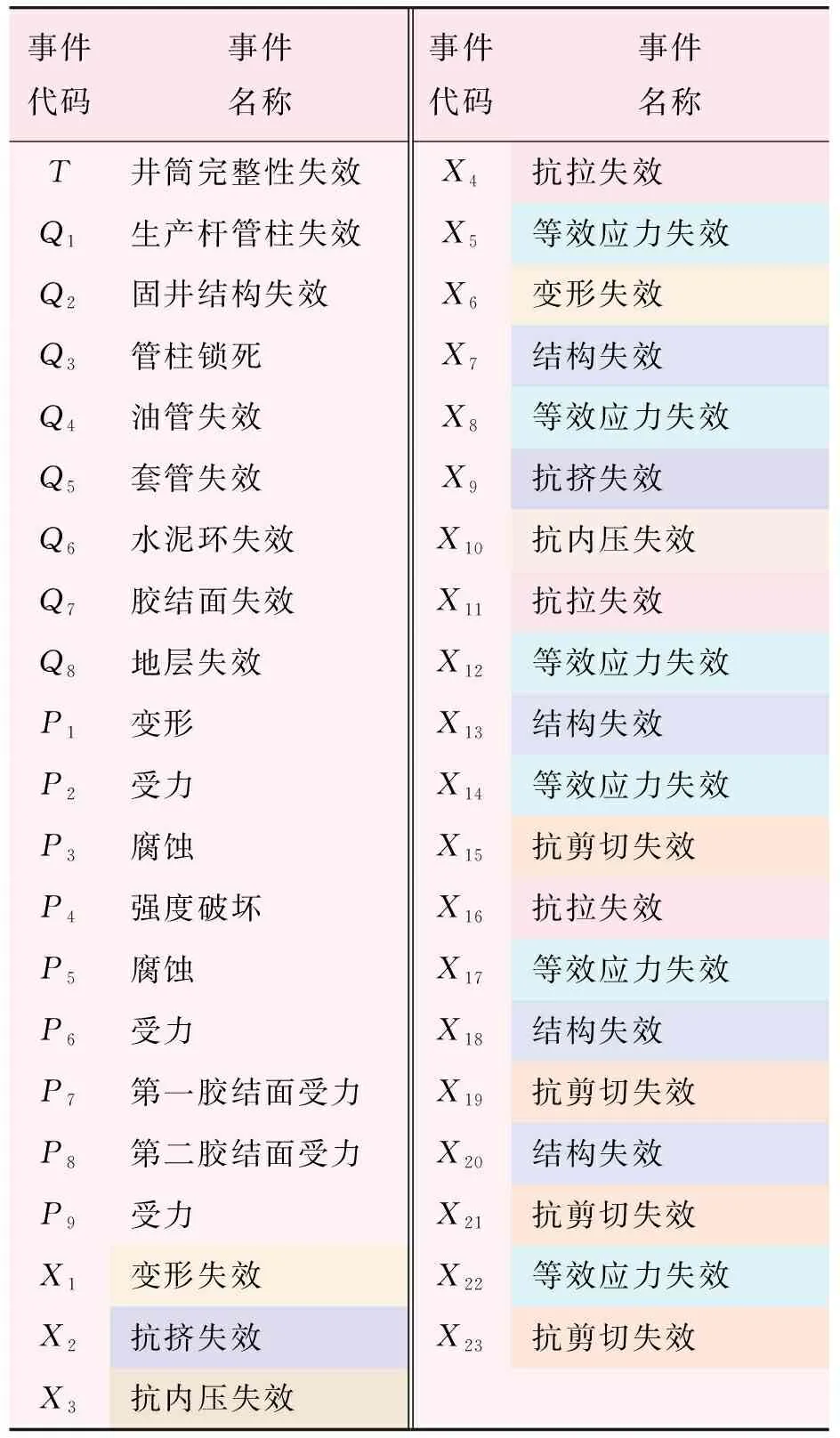
表1 普光T4井筒完整性失效的贡献因素及代码

图3 普光T4井筒完整性失效贡献因素的事件逻辑图

3.2 失效贡献因素的因子分析过程

基于本节推导的因子分析方法，以“失效形式”作为各底事件的分类标签，对上述23类底事件进行归类和压缩。例如，油管、套管、水泥环及地层均存在“强度破坏”这一失效形式(底事件的父类)，因此可以将其各自在“强度破坏”父类下的底事件进行合并、重命名和压缩，这样就有效地减少了统计参数数量，减少可靠性分析的工作量。

利用SPSS统计分析软件将上述井筒完整性失效贡献因素按底事件类型进行分类和合并，并将隶属不同父类的子类参数尽量上移，得到压缩后的井筒完整性失效贡献因素及事件逻辑图如表2和图4所示。可以看出，原本23类失效贡献因素底事件压缩为了7类，即X1、X2、X3、X4、X5、X7和X15，分别对应变形失效、抗挤失效、抗内压失效、抗拉失效、等效应力失效、结构失效和抗剪切失效，每一类底事件对应一种失效判定准则。

在此基础上进行井筒可靠性分析时，仅需参考前文所述的井筒各结构的失效判定方法，按每个底事件的父类对应的失效准则分别进行可靠度计算即可，大大减少了因井筒结构复杂、参数数目 类别众多而造成的工作量。下文进行可靠度计算和完整性分级评价时，即按上述因子分析得到的7类底事件所对应的失效贡献因素为评价指标，通过重要度分析和排名确定具体的失效评价标准。

表2 普光T4井筒完整性失效贡献因素的因子分析结果

图4 普光T4井筒完整性失效贡献因素的因子分析结果事件逻辑图

对上述7类底事件相应的普光T4井筒完整性失效贡献因素进行重要度计算和排名，结果如表3和图5所示。可以看出，套管因发生“等效应力失效”这一底事件对普光T4井筒完整性失效的贡献最大，具有最高的重要度得分3.512分；而套管因“抗拉失效”这一底事件的发生对普光T4井筒完整性失效的贡献最小，具有最低的重要度得分0.019分。说明在所有参与井筒完整性失效分析的贡献因素中，最应该得到注意的参数是套管的等效应力，而应该给予最少关注的参数是套管的拉应力。

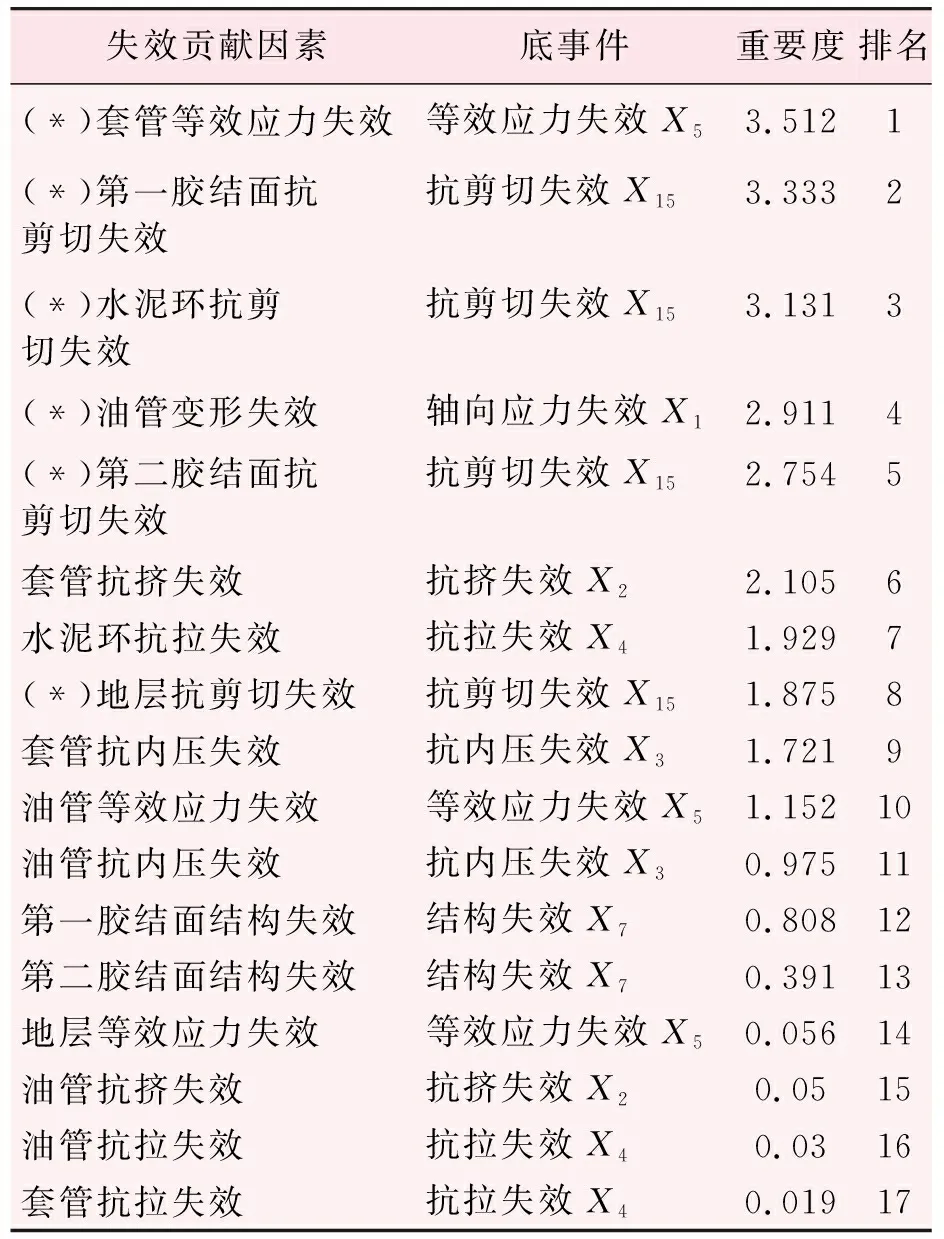
表3 普光T4井筒完整性失效贡献因素的重要度计算结果及排名

表注：带(*)项表示进行井筒完整性的可靠度计算时将使用的失效贡献因素。

对表3和图5其他完整性失效的贡献因素进行同样的分析可知，油管、套管、水泥环、胶结面和地层对普光T4井筒完整性失效最重要的贡献因素分别为：油管轴向应力、套管等效应力、水泥环切应力、胶结面切应力和地层切应力。由前述研究内容可知，井筒完整性失效的发生决定于油管、套管、水泥环、胶结面和地层任一结构或部分发生失效。为精简可靠性分析的模型和步骤，实际应用时可以仅选择上述贡献最大的参数进行分析，所得的可靠性结果足够满足工程中的设计和校核需要。

3.3 失效贡献因素的重要度累计结果

图6为各井筒完整性失效贡献因素对应的底事件在普光T4井筒完整性评价中的重要度累计结果直方图。

从图6和图5中可以看出，底事件“抗剪切失效”对顶事件“普光T4井筒完整性失效(T)”的贡献最大，累计重要度达到了11.093；而底事件“结构失效”对顶事件“普光T4井筒完整性失效(T)”的贡献最小，累计重要度仅有1.199。上述认识对油气田实际生产作业和井筒设计、施工具有重要的指导意义。

图5 普光T4井筒完整性贡献因素的重要度对比

图6 普光T4完整性失效贡献因素对应底事件的重要度累计结果

4 结论

a)在进行复杂油气井井筒完整性分析时，采用因子分析法可以有效地指导在设计过程中和施工作业前的数据采集及处理工作，过滤不必要的统计数据，减轻工作量。

b)“抗剪切失效”对普光T4井筒完整性失效的贡献最大，累计重要度达到了11.093；而“结构失效”对顶事件普光T4井筒完整性失效的贡献最小，累计重要度为1.199。

c)对因子分析得到的重要度高、失效贡献大的参数或底事件类，应给予重点关注，可以有效减轻数据统计人员和可靠性分析人员的工作量，实现效率和效果的双重提高，切实为工程实际作业提供指导。