基于EGM2008在GPS高程转换中的精度分析

姬 洪 亮

(新疆维吾尔自治区交通规划勘察设计研究院，新疆 乌鲁木齐 830006)

1 概述

EGM2008(Earth Gravitational Model 2008)地球重力场模型是美国国家地理空间情报局(National Geospatial-Intelligence Agency，NGA)在2008年4月推出的新一代全球重力场模型，NGA经过多年的探究和研制，充分利用以往建立的地球重力模型的理论成果与实验数据，数据来源主要有地面重力、卫星重力、卫星测高等，采用先进的建模方法和技术完成的地球重力场模型。EGM2008模型可以提供一下成果：全球重力场模型(2 190阶次)；全球 5′×5′空间分辨率的重力异常；全球 5′×5′网格垂线偏差；全球 5′×5′,2.5′×2.5′,1′×1′网格大地水准面[1]。

EGM2008在长达4年的模型研制周期中，曾委托很多国家和地区对模型结果进行评估与测试，从而使模型不断的趋于完善，表1的外部检测结果表明，EGM2008模型在全球很多国家和地区都具有很高的精度。国内很多学者以及技术人员也开展了基于EGM2008进行高程转换在中国大陆的适用性分析，并进行求解高程异常的精度分析结果如表2所示。

表1 EGM2008在全球的精度情况[2]

表2 EGM2008在中国大陆的精度情况[3]

以上研究成果在宏观上肯定了EGM2008模型在全球多个国家和地区以及我国大陆的精度适用性和可靠性，本文以新疆某建设工程为例，对EGM2008模型在GPS高程转换方面进行应用研究及精度分析。

2 EGM2008高程转换原理及方法

GPS观测采集到的高程是基于WGS84椭球的大地高，而实际工程建设中需要的是控制点基于似大地水准面的正常高，大地高与正常高之间的转换关系可表示为：

H=ξ+h

(1)

其中，H为大地高，通过GPS观测所得；h为正常高，通过水准测量所得；ξ为高程异常值，高程异常值的解算是高程转换中的关键。

高程异常值是地球重力场的重要参数之一，通过EGM2008并结合GPS点位置数据，可以直接解算出GPS点的高程异常值。EGM2008高程异常值计算公式为[4]：

(2)

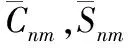
但是EGM2008定义的模型高程基准与我国采用的国家高程基准不一致，它们之间存在着一个系统差，因此通过EGM2008求得高程异常值进一步推算正常高时，式(1)演变为：

H=ξM+h+Δh

(3)

其中，Δh为EGM2008定义的高程基准与国家高程基准之差，即为高程异常差值，可通过引入已知控制点的大地高和正常高推算Δh，但每一个地方的Δh都不一样，因此准确的找到每一地方的Δh是本文讨论的重点。

3 工程案例分析

本文以新疆某带状工程项目为例，路线自东北向西南方向延伸，所经区域为戈壁、微丘、低山地貌，地势没有较大起伏，测区内最高海拔约为1 200 m，最低处海拔约为750 m，该项目全长约280 km，均匀布设97个D级/四等平面高程控制点。D级GPS控制网测量采用经过国家计量检定机构质检的8台Trimble R4双频GPS接收机同步观测，采用静态定位观测模式，以混连式组网，观测时间不小于60 min，数据采样间隔为15 s，网平差处理采用天宝TBC软件处理完成。四等水准控制网以测绘局提供的多个国家二、三等水准点为起算点，采用后、前、前、后观测顺序，按中丝读数法进行符合路线水准观测，观测数据利用南方平差易进行平差，平差结果满足GB/T 12898—2009国家三、四等水准测量规范要求，最终获得各控制点正常高。

在外业GPS网观测结束后，采用TBC软件进行无约束平差得到全部控制点的WGS84坐标，将WGS84坐标十进制经纬度输入“AllTrans EGM2008 Calculator”软件利用双线性插值法(Bi-linear Interpolation) 获得每一控制点基于EGM2008的高程异常值ξM。分别通过均匀分布在路线两端及中间的已知水准高的控制点作为基准点，采用已知2点、3点、5点、9点四个方案进行高程拟合，方案1中基准点离未知点最远距离为142 km，方案2中基准点离未知点最远距离为72 km，方案3中基准点离未知点最远距离为37 km，方案4中基准点离未知点最远距离为20 km。通过高程拟合得到的正常高与水准测量得到的结果进行对比分析，希望能够得到有意义的结论。

以9点方案为例，在知道9个基准点由EGM2008算出的高程异常值ξM、大地高H和正常高h后，可以算出该点的高程异常差值Δh。通过图1我们可以看出Δh与点的位置关系密切，即可得到Δh与位置坐标的相关函数[5]：

Δh=a0+a1x+a2y+a3x2+a4xy+a5y2+…

(4)

其中，x,y均为点位坐标;a0,a1等为多项式待定系数。通过最小二乘原理和已知控制点数据推算出上式的待定系数，进而将未知点坐标代入式(4)中即可得到该点的高程异常差值Δh，最终推算得到未知点的正常高。

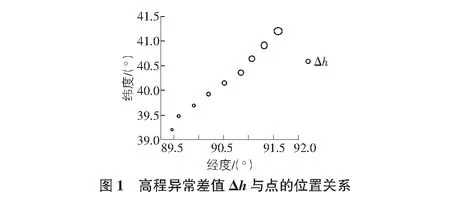
如果将水准测量得到的正常高作为真值，通过EGM2008推算得到的各点正常高与其进行对比分析可得出以下结果如表3,表4所示。

表3 EGM2008推算结果检核统计

表4 差值分布统计

方案1中在路线两端布设两个基准点，未知点与基准点距离最大为142 km，进行高程转换结果与真值进行比较最大值为8.8 cm、最小值为-62.4 cm、平均值为-22.6 cm、中误差为31.3 cm，差值大部分大于20 cm；方案二在路线均匀布设三个基准点，未知点与基准点距离最大为72 km，高程转换结果与真值比较最大值为22.3 cm、最小值为-48.8 cm、平均值为-9.1 cm、中误差为23.4 cm，差值精度明显提高，但差值仍然大部分大于20 cm；方案3在路线均匀布设5个基准点，未知点与基准点距离最大为37 km，高程转换结果与真值比较最大值为29.7 cm、最小值为-40.0 cm、平均值为-5.9 cm、中误差为18.6 cm，差值小于20 cm的比例可以达到70.1%；方案4在路线均匀布设9个基准点，未知点与基准点距离最大为20 km，高程转换结果与真值比较最大值为19.6 cm、最小值为-10.9 cm、平均值为1.7 cm、中误差为13.0 cm，全部点差值均小于20 cm，小于10 cm的比例可以达到88.7%。

4 结语

本文依据作者实践工作中的一个项目通过EGM2008模型进行GPS高程转换，对转换结果进行比较和处理，得出一些有益的结论：

1)EGM2008在GPS高程转换中的精度与基准点的数量成正相关，与转换点到基准点的距离负相关；当基准点与转换点距离小于20 km时，转换精度就能够保证在20 cm以内，能够满足大部分精度要求不太高的工程。

2)基于EGM2008的高程转换在只需要少量已知点的情况下，就能够推算出测区内其他点的高程，对联测困难、基准点少的情况，可以充分利用本方案，从而减少工作强度、降低投入成本、提升工作效率，有较好的现实意义。