脉冲压缩雷达的信号包络及检测模型研究

邹本振,张 萌,王 朝

(中国电子科技集团公司第二十九研究所，四川成都 610036)

0 引 言

传统的雷达和电子战装备的数字仿真建模，一般分为数字信号级、功能级或效能级两类。信号级模型对装备各个关键环节的信息处理过程进行仿真；功能级模型主要以各类能量方程为理论基础，一般仅对信息装备最终的战技术指标和装备效能进行计算和评估，而不对信息处理的过程进行仿真。相较而言，信号级仿真模拟了电子信息装备的实际工作过程，但实时性较低，不容易满足各类作战推演或仿真系统的工程化应用要求；功能级模型运算效率高，但一般忽略了电子信息装备各类检测判决的概率性问题，容易给作战人员造成误解。

本文以脉冲压缩雷达装备建模为例，从对雷达信号包络特性的推导和分析入手，抛开繁杂的IQ数字信号处理运算过程，通过分析雷达信号处理各个关键环节对信号幅度和包络形状的影响，推导拟合出经过脉压、加权、融合、并叠加噪声后的信号检测包络，以此为基础，将原有功能级模型中单纯以信噪比为检测标准的目标判决，替换为真实装备中以虚警概率为基础的CFAR判决，用这种方法兼顾了细粒度建模中探测的概率性问题以及工程化应用的效率问题。

1 雷达信号处理链路分析

雷达接收机从天线接收到信号，与本振混频后变成中频信号，然后经过数字下变频(或经过模拟IQ解调后跟基带A/D转换)后，形成IQ复包络数字信号，随后两路IQ信号送入信号处理机进行数字处理。一个典型的脉冲压缩雷达的信号处理链路如图1所示，图中FFT和检波后积累一般是二选一以实现不同的多脉冲融合处理技术。

图1 典型脉冲压缩雷达信号处理链路

对天线接收来的模拟信号到基带IQ数字信号的转换是由接收机物理硬件完成。在不考虑精度、稳定性和其他因素(如AGC限幅等)情况下，在雷达仿真建模时，假定这种模数转换并不对信号波形包络造成改变，那么如果IQ数字信号直接送至包络检波器，其输出的噪声将符合瑞利分布，而信号符合莱斯分布。但实际上如图1所示，现代雷达很多采用了脉压和多脉冲融合等信号处理链路，这些处理不仅对包络幅度造成影响，而且会改变包络的形状，单纯用莱斯分布无法直接描述信号的包络分布特性。

信号处理机输入端的IQ数字信号同时携带了振幅和相位信息，而送入CFAR检测的仅有信号的包络振幅，相位信息作为中间数据，在辅助信号处理机完成信噪比的提升后将会被舍弃。因此这里主要从信号的包络角度，分析信号处理机中脉冲压缩、加权、脉冲积累对信号波形形状和幅度的影响，进一步推导拟合出噪声基底和信号的包络，为信号检测提供完整的输入。

2 雷达信号包络求解

2.1 基于瑞利分布的噪声包络

没有目标回波的情况下，雷达接收机内部的噪声符合高斯正态分布，高斯噪声通过窄带中频滤波器再加到线性包络检波器后，其包络振幅将符合瑞利分布特点[1]，其概率密度函数为

(1)

式中r代表噪声的包络振幅，σ2是噪声功率。在雷达系统中，如果r0是线性接收机的输出，令

(2)

设u服从[0,1]的均匀分布，则瑞利随机变量取值如下：

(3)

利用这个方法仿真的2000个瑞利变量及其统计概率如图2所示。在上式中，雷达接收机内部噪声功率σ2计算如下：

σ2=kT0BFn

(4)

其中k是波尔兹曼常数(1.38×10-23J/K)，T0是基准温度(290 K)，B是接收机带宽，Fn是接收机的噪声系数。

2.2 基于莱斯分布的带噪信号包络

经过中频滤波和包络检波器后，一个振幅恒定的目标信号叠加噪声后，符合莱斯概率密度函数分布[1]，又称广义瑞利信号，其概率密度函数如下：

(5)

式中A为信号幅度，σ2为噪声功率，I0(·)为第一类零阶修正贝塞尔函数。仿真时，只要在正态分布随机总体中抽取两个相互独立的均值为零的正态分布随机数U、V，再在其中的一个上加个常数A，便可获得广义瑞利分布随机数。

下面我们假定已经产生了瑞利随机变量r0，然后将信号r0作如下处理：

(6)

式中θ为[0,2π]区间上的均匀分布随机变量，则广义瑞利随机变量r1为

(7)

当A=0时，r1=r0，变为瑞利分布；当SNR=A2/2σ2很大时，近似变为服从均值为A、方差为σ2的高斯分布，其概率密度函数如下：

(8)

雷达信号经天线到达接收机处的功率Ps可由雷达方程得到：

(9)

式中Pt为发射信号的峰值功率;G为收发共用天线的增益;λ为信号波长;σRCS为目标散射截面积;R为目标距离;Ls为系统损耗。

图2 瑞利随机变量及概率分布

图3 莱斯随机变量及概率分布

图4 复合信号

2.3 脉冲压缩包络输出

如果不计较由信号波形调制导致的信号包络形状的变化，就可以基于瑞利分布和莱斯分布完成对噪声和信号包络的简单重建，如图4所示。实际上很多雷达采用了脉冲压缩的脉内调制方法以期望得到更好的信噪比增益和目标分辨率，这对信号包络的幅度和形状都会造成影响。以LFM波形为例，其信号复包络由幅度和相位调制函数表达为

(10)

式中A为信号幅度，B为扫频带宽，T为发射脉冲宽度。利用频域方法进行脉冲压缩时，当时带积BT很大时，脉冲压缩输出的频谱W0(f)在频率-B/2和+B/2之外的能量可以被忽略[2]，其幅度谱近似矩形，表示如下：

(11)

其中，rect(f/B)对应的傅里叶变换对如下：

(12)

因此，经过逆变换后的脉冲压缩输出包络如下：

(13)

假设信号幅度A为1，带宽B为9 MHz，脉宽T为6 us，采样率为18 MHz，其包络及采样见图5所示。

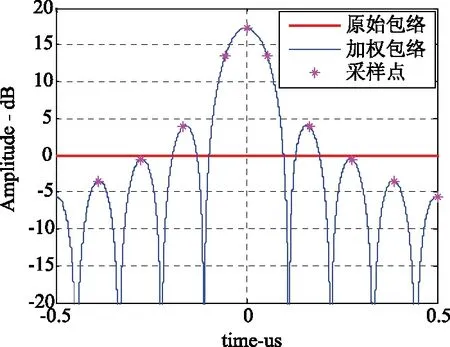
图5 脉压信号包络及采样

2.4 加权滤波器的包络输出

输入的LFM线性调频信号经过脉压处理得到sinc函数的包络，会产生时间副瓣，其第一旁瓣仅有-13.2 dB，很可能在CFAR检测时被当做噪声基底，使得主瓣信号无法被正常检测出或掩盖了旁边的较弱信号。这种旁瓣特性并不是雷达接收机想要的效果，因此，常常引入加权(加窗)的办法来降低旁瓣电平。常见的加权函数有泰勒加权和余弦平方加基座加权。以余弦平方加基座加权为例，其加权函数的形式为：

(14)

底座高度H分别为0、0.08、1时对应了常见的汉宁、海明和均匀加权，其加权函数经过变换得到：

(15)

余弦平方加基座加权滤波器的脉冲压缩输出为

W(f)=W0(f)[H+(1-H)cos2(πf/B)]=

(16)

其中，-B/2≤f≤B/2，逆变换得到加权滤波器的输出包络为：

(17)

可以看出，它的时间函数是三个时间位置不同并经加权的sinc函数组合而成。加海明窗的仿真如图6所示，相比于加窗前，其副瓣峰值电平由-13.2 dB变为-42.8 dB，效果明显，但其3 dB主瓣宽度则由0.886/B变为1.33/B，同时增加了一定的损耗。

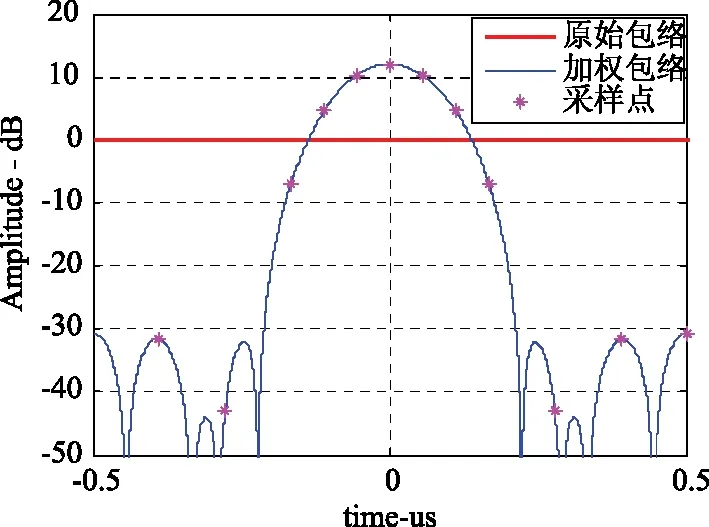
图6 海明加权信号包络及采样

2.5 信号包络的融合处理

(18)

Pn=npσ2

(19)

非相干融合是在包络检波器后的脉冲融合，如果已经模拟出每一帧信号加噪声的完整包络，那么直接将N个信号的相应距离门采样点相加即可，这符合雷达检波后积累的原理。

非相干融合也可以通过计算融合后的积累增益，依据信号幅度和功率之间的平方根关系，反推出其信号幅度的变化。多脉冲进行非相干融合时虽然失去了相位信息，但脉冲之间并不完全是随机的关系，因为它们毕竟是从同一个目标按照相同PRI间隔先后返回的相关联的信号，其融合后的信噪比仍然得到了一定程度的提高。其融合增益可由meyer函数[5]反推获得，meyer函数的形式如式(21)所示，其输出探测概率Pd是由非相干脉冲积累个数N、虚警概率Pfa、信噪比SNR和Swerling目标起伏模型共同决定的。

Pd=meyerfun(N,Pfa,SNR,Swerling)

(20)

在设定Pd、Pfa、Swerling不变的情况下，令脉冲融合个数分别设置为N=0和N=np，通过反推遍历可以分别得到(SNR)1和(SNR)NCI两个值，两个结果之间的比例因子就是非相干融合增益I(np)，如下式所示。

(SNR)NCI=(SNR)1×I(np)

(21)

3 雷达信号检测包络模型

3.1 雷达信号检测包络的快速拟合

从以上的推导分析来看，如果信号的幅度保持不变为A，那么叠加噪声σ2后，在其信号持续时间Tpw内，其包络将服从莱斯分布，即广义瑞利分布；虽然脉压和加权改变了信号包络形状，使得其振幅恒定的条件发生了变化，但在某个瞬时采样点，仍然可以认为在持续时间Tpw→0内，其包络满足幅度为A′、噪声功率为σ2的莱斯分布。只不过从宏观角度来看，幅度A′是随时间而变化的。因此从整个时域分布来看，我们可以快速构建检测包络如下：

(1)基底噪声包络服从信号幅度为0、噪声功率为σ2的莱斯分布，即瑞利分布；

(2)脉压前的带噪信号包络服从信号幅度为A、噪声功率为σ2的莱斯分布；

(4)加权后的信号幅度函数由三个不同系数的辛格函数构成(以余弦平方加基座加权为例)，见式(15)，脉压和加权信号叠加噪声后的包络图7和图8所示，图中模拟的脉压前的信噪比约为10 dB，可以看出加权后的包络旁瓣采样点主要由噪声起作用，而主瓣受噪声的影响较小，符合实际情况；

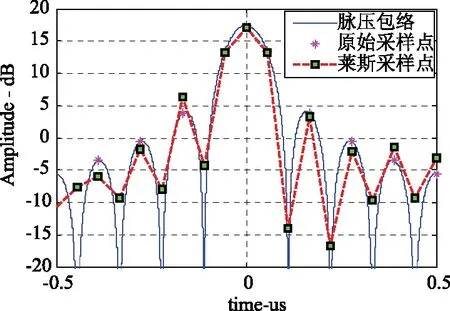
图7 叠加噪声后的脉压信号包络

图8 叠加噪声后的加权信号包络

(5)对于相干多脉冲融合，其带噪信号包络服从信号幅度为npA、噪声功率为npσ2的莱斯分布，见式(18)和式(19)；

(6)对于非相干融合，可以将每一帧的信号加噪声的包络采样点直接相加求和，也可以通过计算积累增益反推出信号幅度的变化情况。

通过以上分析，以脉压信号为例，分别生成一定数量的瑞利噪声采样点和莱斯带噪信号采样点，并依据目标距离，将噪声和信号进行拼接组装，最终拟合成完整的包络模型如图9所示。图中模拟的基底噪声功率为0 dB，两个信号在脉压前具有相同的信噪比，约为25 dB，第一个信号没有进行加权处理，第二个信号使用了海明加权。可以看出在当前的信噪比下，海明加权的旁瓣几乎可以认为与内部噪声有等效的输出，而没有加权处理的旁瓣则不可忽略，这跟实际情况也是一致的。

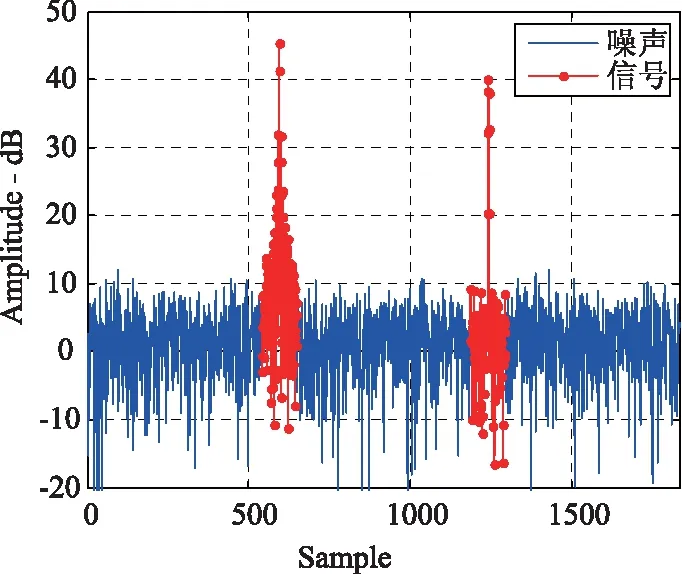
图9 拟合包络模型

3.2 CFAR检测及仿真

对于常规雷达，一般采用CFAR恒虚警的方法进行检测，CFAR门限thr的取值只跟虚警概率Pfa和参考单元个数navgcells相关，是一个相对门限，求解如下[4]：

(22)

但上式仅适用于单脉冲情况下的CFAR门限选取方法，实际上由于非相参积累存在求和的过程，其噪声采样的统计规律将发生变化[6]，导致公式(22)不再适用。杨建桥[7]给出了虚警概率由参考单元个数、非相参积累个数和CFAR门限共同决定的简约数学表达式，可以据此反求出非相参积累下的CFAR门限，这里不再详解。另外一般在CFAR检测器中都要设置保护单元，采用的计算方法如式(23)所示，其中S是采样率，Bcompressed是压缩脉冲的带宽：

(23)

此处设定保护单元为2个，参考单元为50个，模拟基底噪声为0 dB，模拟的两个信号的信噪比(脉压前)分别为25 dB和0 dB，并采取单元平均恒虚警(CA-CFAR)的方法进行CFAR检测。当虚警概率设置为10-3时，出现噪声被误检测为信号的现象(第一个和最后一个)，如图10所示，经过多次测试，噪声虚警的次数与噪声采样点数的比值与设置的虚警概率相当；当虚警概率设置为10-7时，CFAR门限约为12.8 dB，第二个较弱信号脉压后的峰值信噪比(时带积)为17 dB，由于受到噪声的调制影响和参考单元点数的限制，第二个信号有时无法被检测出，如图11所示；图12是图11中第一个信号附近的局部放大图，可以看出检测门限在信号前后出现较大的提高，在信号峰值采样点附近又迅速降低，使得信号被检出。

图10 CFAR输出1(虚警概率为10-3)

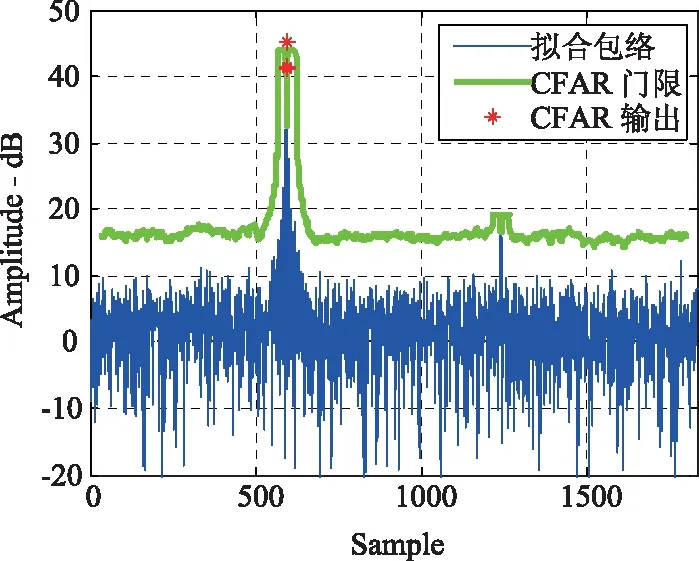
图11 CFAR输出2(虚警概率为10-7)

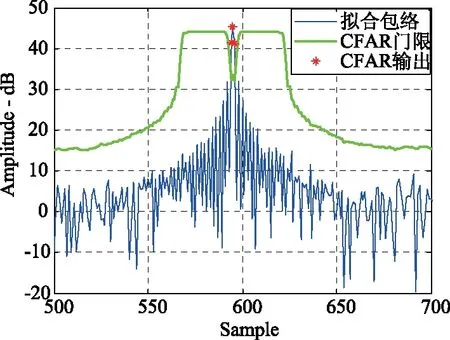
图12 CFAR输出3

4 结 语

本文基于信号和噪声的概率统计特性，以及信号处理的机理，以典型脉冲压缩雷达为例，求解并拟合出了叠加噪声，并经过脉压、加权、多脉冲融合后的信号检测包络，并基于此进行了目标检测仿真。这种新的思路和方法，可以直接应用到雷达装备功能级建模与仿真中去，同时可以借鉴应用到包括电子战在内的其他电子信息装备建模中，以支撑各类电子信息装备和系统的细粒度仿真。