基于双层迭代的孤岛微电网前推回代潮流计算

秦 政，常俊晓，高 挺，陈音璇

（国网浙江省电力有限公司台州供电公司，浙江 台州 318000）

0 引言

微电网是由DG（分布式电源）、负荷、能量转换装置、储能装置、监控与保护装置等组成的小型配电系统，具有运行方式、控制模式灵活多变等特点，能高效地实现多类型DG就地分散并网，已成为新一代智能配电网的重要组成部分[1-2]。正由于微电网运行方式、控制模式的多样性，使得传统的配电系统潮流计算方法不适用于微电网的潮流计算，因此，必须针对微电网的运行控制策略来计算其潮流分布。

微电网的运行方式主要分为并网运行和孤岛运行2种[3]。在并网运行模式下，配电系统可以为微电网提供稳定的功率，以维持微电网的频率恒定，一般将并网点设置为平衡节点，而所有的DG节点一般设置为PQ节点或PV节点[4]，因此在并网运行模式下，微电网的潮流计算方法与传统配电系统潮流计算方法并无本质区别。在孤岛运行模式下，当DG采用主从控制模式时，主控DG节点一般选取调节容量较大的DG节点作为全网平衡节点，而其他从控DG节点则设置为PQ节点或PV节点，同样，传统配电系统潮流计算方法也能适用于采用主从控制策略的微电网潮流计算。当DG采用对等控制策略或者分散下垂控制策略时，由于DG节点均为下垂节点，全网无平衡节点，微电网的频率会因缺乏足够的功率支撑而偏离额定值，致使微电网潮流计算的物理模型参数（如线路阻抗）发生变化，因此，在传统配电系统潮流待求节点电压幅值和相角的基础上，增加了频率作为待求量，显然，传统配电系统潮流计算方法不适用于无平衡节点的孤岛微电网潮流计算[5-6]。

针对无平衡节点的孤岛微电网潮流计算，文献[7]在经典牛顿-拉夫逊潮流方法的基础上增加系统有功功率、无功功率对频率偏差的修正量，以适应多个DG共同承担全网的功率不平衡量。文献[8]将多个DG节点设置为松弛节点，同样采用牛顿-拉夫逊法求解三相不平衡的孤岛微电网潮流。虽然牛顿-拉夫逊潮流方法普遍适用于所有类型的网络结构，但对于辐射状的微电网来说，其固有的雅克比矩阵求逆过程使得其求解效率不高。文献[9]将DG节点处理为PQ节点、PV节点和下垂节点3类，将非线性潮流方程组的求解问题转化为求解无约束最优化问题，并采用基于BFGS修正的信赖域算法求解，以避免雅克比矩阵求逆来减少计算量。前推回代法[10-12]由于求解过程简单、收敛性较好等优点被广泛应用于辐射状的配电系统潮流计算，但该算法并不能很好地求解无平衡节点的孤岛微电网潮流问题，一直以来都未能推广到采用下垂控制策略的孤岛微电网潮流计算。

因此，本文对传统的前推回代法进行改进，通过设置“虚拟根节点”，采用内外双层迭代以适应无平衡节点的孤岛微电网潮流计算：在内层采用传统的前推回代法；在外层采用频率和电压联合修正。最后，通过孤岛运行的IEEE 33节点系统验证算法的正确性和有效性。

1 孤岛微电网潮流计算模型

1.1 静态负荷模型

不同于传统的配电系统潮流模型，采用分散下垂控制策略的孤岛微电网稳态频率并不是预先设置的工频，而是在工频附近波动，且这种频率波动会造成线路阻抗的变化。而负荷也是随电压和频率变化的函数，因此，本文采用静态负荷模型[13]来描述负荷节点电压和频率变化对输出功率的影响， 具体如式（1）、式（2）所示：

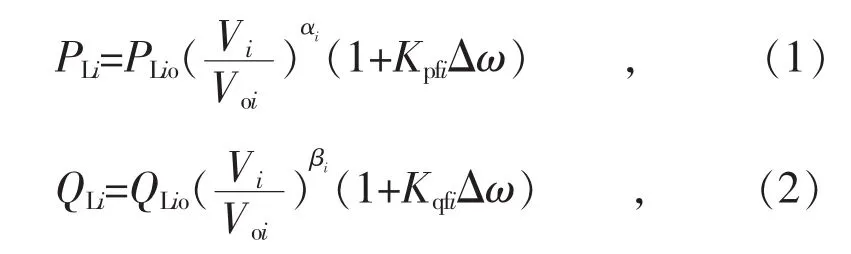
式中：PLi和QLi分别为负荷节点i实际的有功功率和无功功率；PLio和QLio分别为负荷节点i额定的有功功率和无功功率；αi和βi分别为反映节点i电压变化对节点i有功功率和无功功率影响的指数系数；Voi和Vi分别为负荷节点额定电压和实际电压；Kpfi和Kqfi分别为反映系统频率变化对节点i有功功率和无功功率影响的增益系数；Δω=ω-ωo， 为系统实际频率 ω 与额定频率 ωo的偏差。

1.2 DG模型

在微电网中，大部分DG都是通过逆变器的电力电子接口并网，在忽略逆变器等设备的非线性情况下，在采用下垂控制策略的孤岛微电网中，DG的输出有功功率与频率、输出无功功率与电压均成近似线性关系，可采用式（3）-（4）描述：

式中：PGi和QGi分别为DG节点i实际输出的有功功率和无功功率；PGoi和QGoi分别为DG节点i额定输出的有功功率和无功功率；mpi和npi分别为DG输出的有功功率和无功功率的静态下垂系数；VGi和VGoi分别为DG节点i的实际电压和额定电压。

2 改进前推回代法的孤岛微电网潮流计算

2.1 内层迭代过程

本文采用基于BIBC（节点注入电流-支路电流）关联矩阵和BCBV（支路电流-节点电压）关联矩阵的直接前推回代法[14]。所谓BIBC矩阵，顾名思义就是每个支路电流和节点注入电流之间的关联矩阵；而BCBV矩阵，就是每个支路电压和节点电压之间的关联矩阵。与传统配电系统直接前推回代法不同的是：孤岛微电网无平衡节点，即前推回代的根节点不存在，为此，本文通过设置一个“虚拟的根节点1”，将其连接至任意一个根节点母线，形成BIBC矩阵和BCBV矩阵。虚拟根节点的选取原则是任意的，但是虚拟根节点选择不恰当可能导致迭代不收敛，所以通常选取孤岛微电网的并网点，通过迭代设计使得该节点流向微电网的功率为零，故将此节点称为“虚拟根节点”。

首先假设系统的频率偏差为0，所有节点电压为1，各个DG的输出有功功率和无功功率分别为：

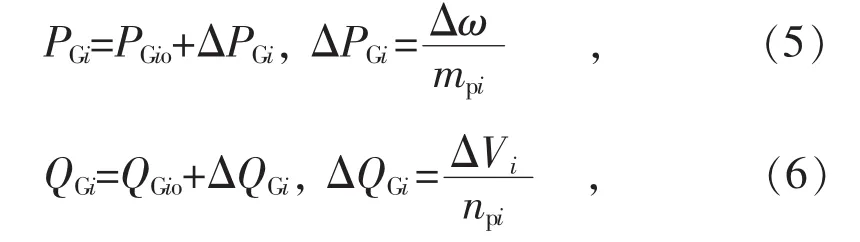
式中：ΔPGi是由于频率偏差造成的DG输出有功功率增量；ΔQGi是由于电压偏差造成的DG输出无功功率增量。

然后根据各个节点的注入视在功率Si计算出节点的注入电流Ii，计算公式如下：

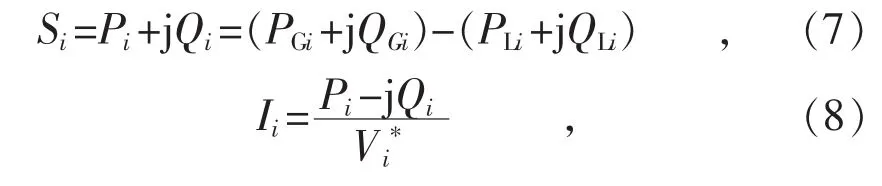
因此，基于BIBC矩阵很容易得到每条支路的电流向量B为：

式中：I是所有节点的注入电流Ii形成的列向量。对于n个节点（包括虚拟根节点）的辐射状微电网拓扑结构，支路电流向量B为n-1维，BIBC矩阵为n-1维的方阵。

节点电压可以表示为支路电流、线路阻抗和根节点电压的函数[15]，即：

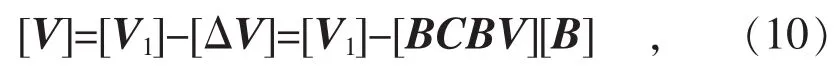
式中：[V1]表示虚拟根节点1的节点电压组成的同维列向量；[V]表示除虚拟根节点1以外的所有节点电压组成的列向量；[ΔV]表示其他所有节点与虚拟根节点1的电压差值；BCBV矩阵即为支路电流-节点电压关联矩阵，它是由线路阻抗组成的n-1维方阵。

进一步利用式（9），可将式（10）改写为：

关于BIBC矩阵和BCBV矩阵的形成在文献[15]有详细介绍，本文不再赘述。上述基于前推回代的内层迭代法可以很好地求解传统配电系统潮流[16]，但是对于下垂控制的孤岛微电网潮流，则明显不能求解，主要是因为没有考虑频率偏移造成的线路阻抗变化，这样BCBV矩阵不再是一个常数矩阵，而是随着频率变化的矩阵。为此，本文在内层迭代的基础上，设计了一个外层迭代过程，以迭代求解孤岛微电网的实际频率。

2.2 外层迭代过程

外层迭代主要是基于虚拟根节点来修正微电网的频率和节点电压。虚拟根节点相当于一个伪主网，因此在内层迭代收敛后有功率会流向或流出虚拟根节点1，而孤岛微电网也未进入一个稳态，通过调整微电网的频率和虚拟根节点1的电压来平衡微电网的不平衡功率。在内层迭代过程中假设虚拟根节点1为系统的平衡节点，微电网系统中的不平衡有功功率ΔP全部由虚拟根节点承担，即：

式中：PG1表示虚拟根节点1的输出有功功率，由于没有电源输出，有功功率置0；V1是虚拟根节点1的节点电压；Bj-1是从虚拟根节点1流向连接节点j的支路电流；real表示取实部。

而不平衡有功功率实际上是由DG共同承担的，即为：

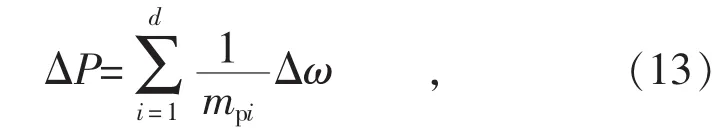
式中：d是微电网中DG的个数。

由此可得孤岛微电网的频率偏差Δω为：

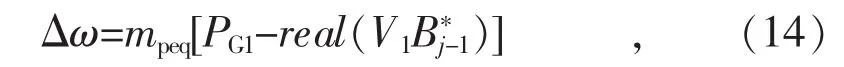
由于频率偏差，线路阻抗也会发生变化，可采用式（15）进行迭代更新：

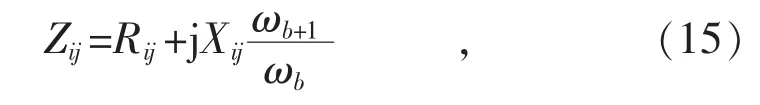
式中：Rij和Xij分别为支路ij之间的电阻和电抗；ωb和ωb+1分别表示b次、（b+1）次迭代的频率。

同样，微电网系统中的不平衡无功功率ΔQ全部由虚拟根节点1承担，即为：

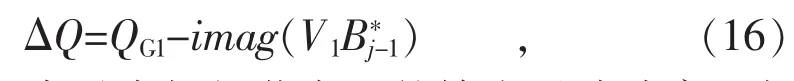
式中：QG1表示虚拟根节点1的输出无功功率，由于没有电源输出无功功率置0；imag表示取虚部。

而不平衡无功功率实际上是由DG共同承担的，即为：

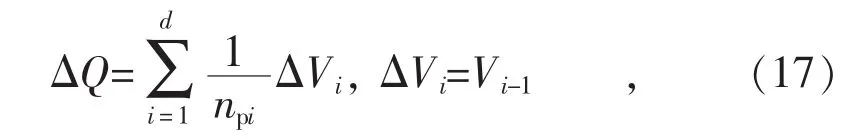
式中：ΔVi是第i个DG的电压偏差，此处认为所有DG节点的电压近似相等，且其中一个DG连接到虚拟根节点，由此可得虚拟根节点的电压偏差ΔV1为：

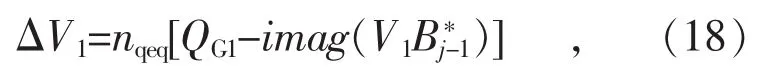
综上所述，本文所提出的改进前推回代潮流计算流程如图1所示：内层迭代是基于BIBC矩阵和BCBV矩阵的前推回代过程，以第a次、第（a+1）次迭代的节点电压偏差作为迭代收敛条件；外层迭代是在内层迭代收敛后进行的电压和频率联合修正，以虚拟根节点1的电压偏差ΔV1趋近于0作为收敛判据。

3 算例分析

本文采用含5个DG的IEEE 33节点作为测试系统，具体如图2所示，系统详细参数见文献[17]。本文将节点1作为虚拟根节点的连接节点，内外双层迭代的收敛精度均设置为10-4，将PSCAD仿真的结果作为参照值，分别采用文献[9]中的BFGS信赖域法和本文所提的MBFS（改进前推回代法）进行对比分析。

3.1 仿真1的对比结果分析

仿真1设置5个DG节点的有功下垂系数依次为-0.04，-1.00，-0.20，-0.50，-0.20； 无功下垂系数依次为-0.04，-1.00，-0.10，-0.30，-0.20。采用本文所提出的MBFS方法进行潮流计算，外层迭代经过8次迭代潮流收敛，而采用BFGS信赖域法进行求解，要经过11次才能达到同样的收敛条件。采用MBFS方法和BFGS信赖域法得到的微电网角频率分别为0.998 4 p.u.和0.998 2 p.u.，而 PSCAD的仿真结果为 0.998 4 p.u.。以PSCAD的仿真结果作为基准，对比采用BFGS信赖域法和MBFS方法得到的节点电压幅值和相角结果分别如图3和图4所示。

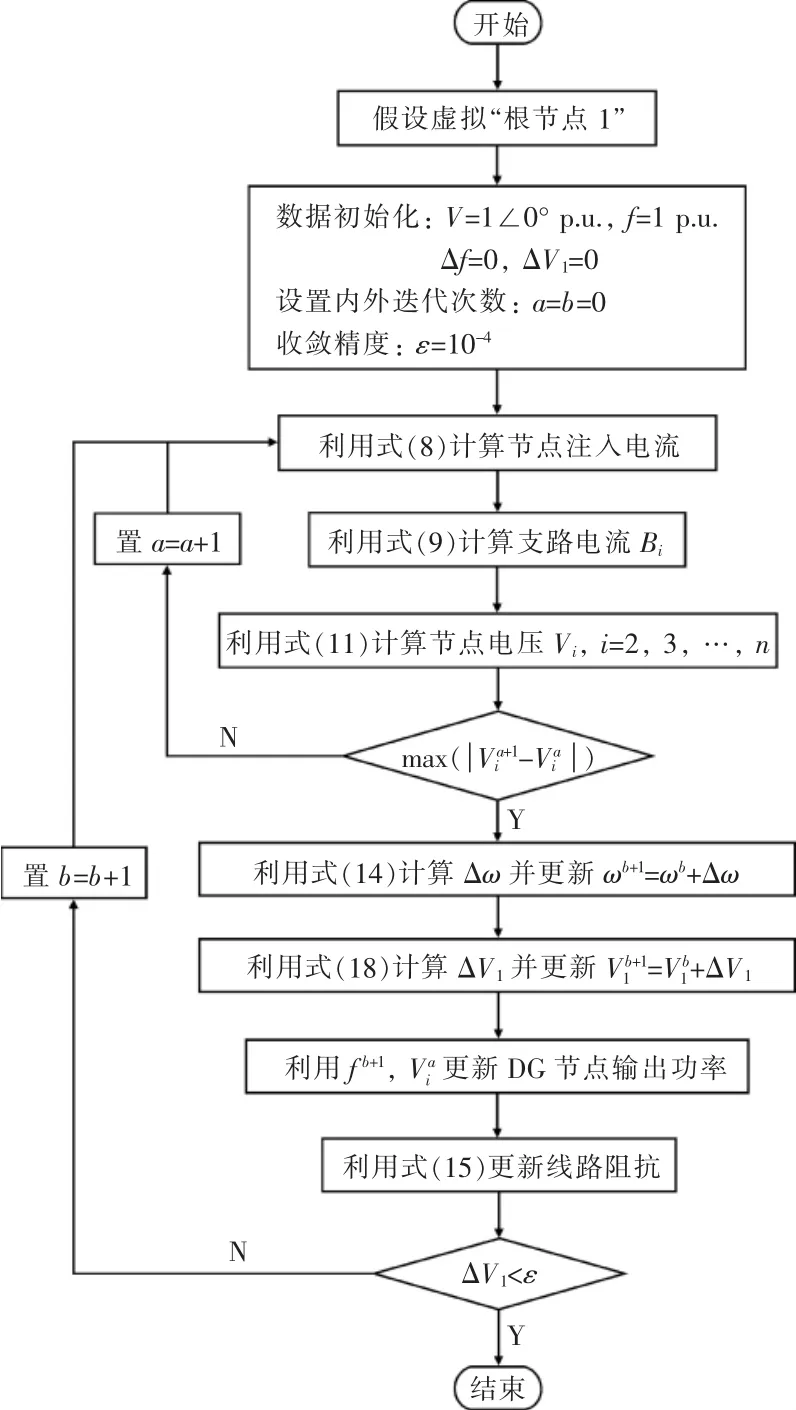
图1 改进的前推回代法计算流程

图2 IEEE 33节点测试系统

图3 3种方法的节点电压幅值对比结果

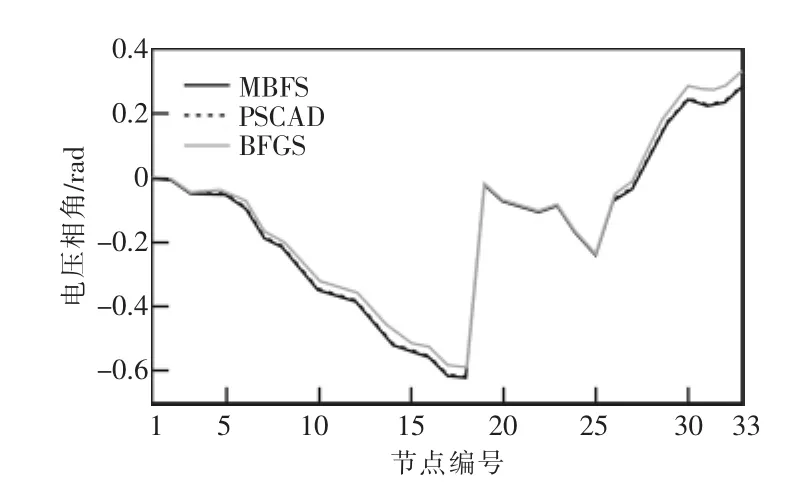
图4 3种方法的节点电压相角对比结果

对比图3和图4中的节点电压幅值和相角不难发现：与BFGS信赖域方法相比，采用MBFS方法得到的节点电压更接近PSCAD的仿真结果，尤其是在电压幅值上，采用MBFS方法得到的节点电压幅值与PSCAD的仿真结果完全一致，而采用BFGS信赖域方法与PSCAD仿真结果误差数量级为10-4；另外，采用BFGS信赖域方法得到的节点电压相角误差较大，采用MBFS方法得到的节点电压相角与PSCAD仿真结果误差数量级为10-4。这主要是由于MBFS方法将电压幅值和相角差作为收敛条件，收敛后的精度达到了10-4，而BFGS信赖域方法是一种优化方法，很容易陷入局部最优，往往取的是次优解。

进一步，图5给出了3种方法的DG输出功率对比结果。同样，采用MBFS方法得到的DG输出功率较采用BFGS信赖域方法更接近PSCAD的仿真结果；很明显，采用MBFS方法得到的DG输出有功功率较无功功率更接近PSCAD仿真结果。究其原因是MBFS方法对所有DG节点的电压采用了“先近似，后修正”的策略，造成了修正DG节点电压误差的不彻底，但采用MBFS方法得到的DG输出无功功率依然优于BFGS信赖域方法。

3.2 仿真2对比结果

为进一步验证本文所提方法良好的适应性，采用表1的3组DG下垂系数，对比采用不同静态负荷模型参数时，采用MBFS方法和BFGS信赖域方法得到的节点电压幅值和相角的最大相对误差，结果如表2所示（此处仍以PSCAD的仿真结果作为基准）。

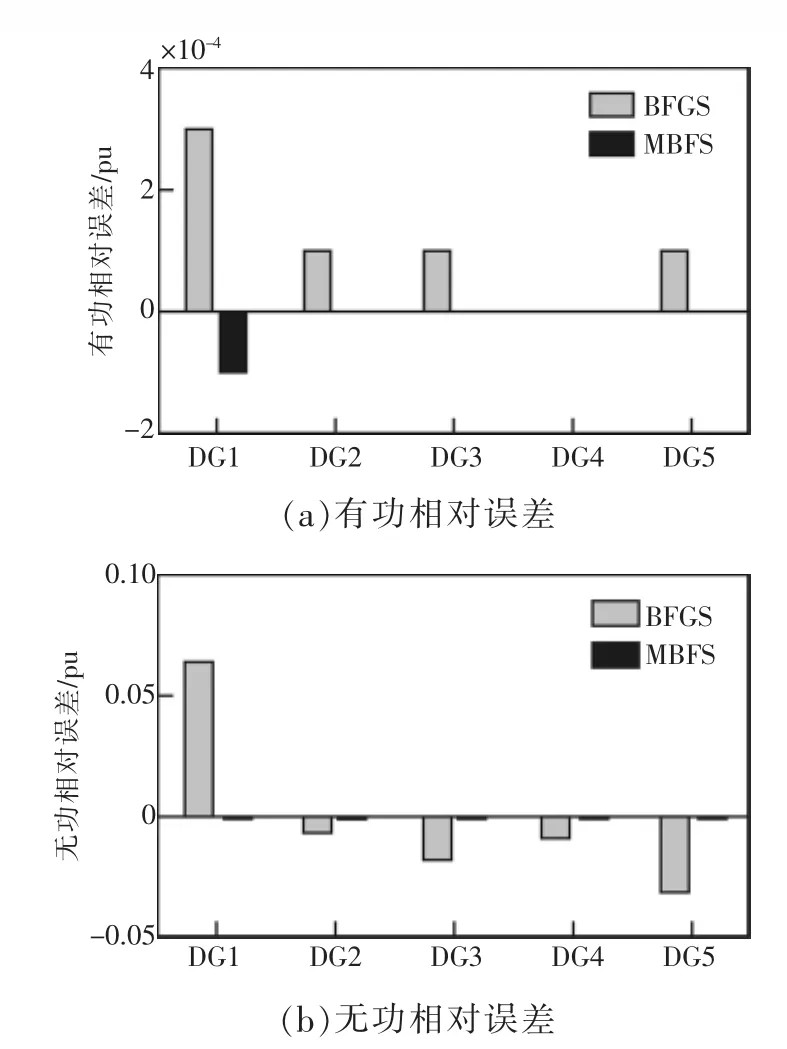
图5 3种方法的DG输出功率对比

表1 DG下垂系数

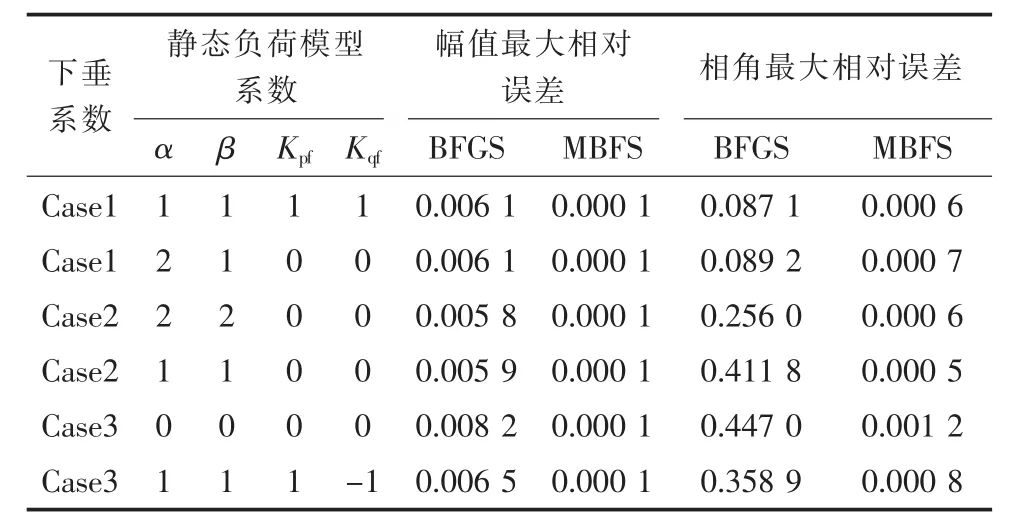
表2 节点电压最大相对误差比较

很显然，采用MBFS方法得到的节点电压幅值相对PSCAD的仿真结果误差始终保持在0.0001；虽然节点电压相角相对PSCAD的仿真结果误差略有波动，但基本上维持在10-4这个数量级上，从而验证了MBFS方法良好的适应性。

4 结语

为解决无平衡节点孤岛微电网的潮流计算问题，本文在前推回代法的基础上进行改进，提出了基于双层迭代的MBFS方法，为孤岛微电网潮流计算提供了一条新的研究思路。该方法基于BIBC矩阵和BCBV矩阵前推回代法，通过设置内外双层迭代，实现了节点电压和频率同步迭代求解。与采用BFGS信赖域方法的对比分析表明：采用本文所提MBFS方法不仅可以得到更为精确的潮流结果，而且可以适用于不同运行模式下的微电网潮流计算。