湿热环境下复合材料层合板本构模型研究及其应用

谢伟，窦鹏鹏，薛展

(西北工业大学 航空学院，西安 710072)

0 引 言

纤维增强复合材料具有许多优点，被广泛应用于航空、航天等各个工程领域。但是其在使用过程中会不可避免地承受温度变化、湿度变化及外部载荷的耦合作用，影响复合材料整体结构的力学性能。

从20世纪70年代开始，国内外对湿热环境下复合材料力学性能进行了大量的试验研究，C.H.Shen等[1]给出了T300/1034层合板在温度范围-73～177 ℃和相对湿度0～100%范围内的拉伸力学性能，并总结了几种材料体系层合板在湿热环境下的性能变化；包建文等[2]对国内生产的T300/5284复合材料在96～98 ℃的蒸馏水中浸泡60 h，研究发现，碳纤维基本不吸湿，而基体材料的吸湿效果较明显；D.Scida等[3]对在70 ℃下吸湿1 300 h后的玻璃纤维/R1二维编制层合板的性能进行试验研究后发现材料的拉伸强度、弯曲强度平均下降53%；J.S.Earl等[4]和B.Guo等[5]分别通过湿热耦合实验，研究了不同复合材料夹层板的各项力学性能随湿热环境因素的变化情况，但没有建立湿热本构方程等理论，也没有考虑损伤的影响；B.Abdel-Magid等[6]的研究发现预加拉伸载荷下玻璃纤维增强复合材料试样吸湿后拉伸强度稍有增加，模量下降，破坏应变增加；李敏等[7]对T700/5428复合材料的吸湿过程和湿热老化后材料的弯曲性能和层间剪切性能进行了试验研究，结果表明湿度对材料的抗弯性能和层间剪切性能有比较明显的影响；J.P.Won等[8]的研究结果表明湿热老化会导致复合材料的内部孔隙增多，拉伸强度下降；G.M.Candido等[9]对环氧树脂基复合材料进行湿热老化后，研究了其力学性能；余治国等[10]通过对T700/环氧树脂及T300/环氧树脂复合材料进行研究，并且对材料老化前后进行了力学性能的检测，试验研究认为，复合材料的吸湿过程是一个缓慢的过程，在湿热环境下，碳纤维/环氧树脂基复合材料的压缩强度会有所下降，保持率均在80%左右；J.Mohan等[11]的研究发现，吸湿对复合材料层合板的断裂韧性有很大的影响，Ⅰ型断裂韧性下降20%，Ⅱ型断裂韧性下降50%。

在理论研究方面，K.H.Amara等[12]系统地研究了湿热老化正交层合板由于基体横向开裂而引起的纵向弹性模量与泊松比的变化，使用两种改进的剪切滞后模型来估计复合材料层合板由于横向开裂所引起的刚度退化；C.K.Kundu等[13]分析了复合材料层合板壳结构在湿热条件下的非线性屈曲变形，但其计算方法只适用于薄壳结构；闫伟等[14]和刘玉佳等[15]建立了湿热力三者耦合的渐进损伤模型，仿真了复合材料层合板在不同湿热条件下的损伤起始及损伤演化全过程，并分析湿热环境对其拉伸、压缩强度的影响；A.Lal等[16]利用细观力学的模型评估复合材料在湿热环境下的力学性能，通过对树脂性能乘以系数Fm进行衰减处理，从而推得退化后的湿热本构方程，该方法只考虑了湿热对树脂性能的影响，对纤维性能的影响略去不计；R.Kumar等[17]则认为湿热环境下复合材料层合板的弹性参数和湿热膨胀系数与温度和湿浓度的变化量存在线性的关系，泊松比受温度和湿度的影响很小，视为不变；Krzysztof Dems等[18]考虑到纤维的截面形状对复合材料层合板的宏观热传导系数的影响时，采用二维模型计算得到了层合板在热载作用下的热传递和热分布，为研究复合材料受热载时的力学行为奠定基础；韩坤华等[19]建立了复合材料双面贴补修理的力学模型，并进行了湿扩散-应力的耦合分析。

综上所述，国内外对该问题的研究目前还没有形成统一的分析与评定方法，而且多数是以试验分析为主，理论方面的研究较少。为了进一步了解复合材料结构在服役期间受湿热环境的影响，需综合考虑载荷和湿热环境变化的作用，开展复合材料在湿热环境下的弹性响应研究，对复合材料的结构设计、制造、使用、维护和寿命预测以及新材料的开发研究方面都具有重要的工程意义。因此，本文首先研究湿热环境下复合材料层合板的渐进损伤模型；然后利用有限元分析软件Abaqus的二次开发接口编写了自定义材料子程序，并预测湿热环境开孔复合材料层合板在拉伸和压缩载荷下的破坏强度和失效模式，验证本文所建立模型的有效性；最后基于该模型提出一种实际工程测量中分离载荷应变与环境应变的方法。

1 湿热环境下复合材料层合板弹性响应预测模型

1.1 正交各项异性复合材料单层板的湿热效应

通过对正交各向异性材料三个材料主方向的单向拉伸试验和三个与材料主方向垂直的平面内的纯剪切试验，得到用工程弹性常数表示的正交各向异性材料的应力-应变关系：

σi=Qijεj(i,j=1,2,…,6)

(1)

式中：Qij为刚度矩阵中的各系数。

(2)

热膨胀系数的单位是1/℃或1/K(K是绝对温度的单位)

由式(2)可得单层板材料主方向热自由应变为

(3)

单层板吸入水分后质量的和干燥状态下的质量比称为单层板的吸湿量，用符号C表示

(4)

式中：m为单层板干燥状态的质量；Δm为吸湿后的质量增量。

参照单层板材料主方向热膨胀系数和热自由应变的定义方法，单层板材料主方向的湿自由应变为

(5)

式中：β1、β2和β3为单层板材料主方向的湿膨胀系数。

单层板材料主方向湿热自由应变为

(6)

由叠加原理，总应变为力引起的应变和湿热自由应变之和，即

{ε}={εM}+{e}

(7)

式中：{ε}为总应变向量；{εM}为由力引起的应变向量；{e}为湿热自由应变。

因此，在外加载荷和湿热的联合作用下，单层板在材料主方向的本构关系为

{ε}=S{σ}+{e}

(8)

式中：S为单层板的柔度矩阵。

所以有

{σ}=Q{ε-e}

(9)

式中：Q为单层板的刚度矩阵。

即考虑湿热变形情况下正交各向异性材料的本构模型为

σi=Qij(εj-αΔT-βC) (i,j=1,2,…,6)

(10)

1.2 湿热环境下组分材料性能的退化模型

在湿热环境下，复合材料单层板除了受湿热自由膨胀影响外，其组分材料的弹性模量和强度等性能也会因环境的影响而变化。本文引入M.Tsai提出的无量纲温度T*[20]，其表达式如下：

(11)

(12)

那么，湿热环境对纤维和基体性能的影响可以用T*的幂函数来近似表达，表达式如下：

(13)

湿热环境对单向板强度性能的影响也可以用T*的幂函数来近似表达，湿热退化表达式如下：

(14)

式中：Xt、Xc分别为单向板纵向拉伸、压缩强度；Yt、Yc分别为单向板横向拉伸、压缩强度；S为单向板剪切强度；a～j为材料湿热退化常数，可通过复合材料手册中常温下和130 ℃下的材料性能常数计算得到，上标0表示室温干态下的材料性能。

为了根据组分材料的力学性能推导出单层板的力学性能，本文采用掺混率法[21]。掺混率法是一种根据纤维和基体的体积分数来计算计算单层板的湿热膨胀系数、弹性模量、剪切模量以及泊松比等参数的方法，公式如下：

(15)

α2=Vf(1+νf)αf+Vm(1+νm)αm-

(Vfνf+Vmνm)α1

(16)

(17)

(18)

E11=Ef11Vf+EmVm

(19)

(20)

(21)

ν12=Vfνf+Vmνm

(22)

式中：α为单层材料的热膨胀系数；β为单层板材料的湿膨胀系数；E为单向板弹性模量；G为单向板剪切模量；ν为单向板的泊松比；下标m表示基体性能，下标f表示纤维性能。

1.3 基于三维Hashin的失效判定准则

复合材料层合板在外载作用下有多种失效模式，包括纤维拉伸失效、纤维压缩失效、基体拉伸失效、基体压缩失效、纤维—基体剪切失效、分层失效和各类组合失效。在加载阶段，层合板中各类失效模式逐渐累积，导致层合板承载能力下降，最终失去承载能力，为了模拟层合板的渐进损伤失效过程，本文采用基于Hashin准则发展得到的三维失效准则[22-23]对单元进行失效判断。

纤维拉伸失效：

(23)

纤维压缩失效：

(24)

基体拉伸失效：

(25)

基体压缩失效：

(26)

基体-纤维剪切失效：

(27)

分层失效：

(28)

(29)

式中：Zt、Zc分别为单向板法向拉伸、压缩强度。在湿热环境下，上述判定准则中的强度采用湿热退化后的值。

刚度退化后复合材料单层板的本构方程表示为

(30)

至此，本文建立了一套完整的湿热环境下复合材料单层板弹性响应的理论模型。需要说明的是，上述公式是基于单层板的，在实际仿真中通过几何上的切割分层模拟不同角度的铺层可以有效地模拟多向铺层层合板。对于各层间的湿热变形的相互作用本文是忽略的，是对模型的一种简化。

1.4 Vumat子程序流程

基于以上理论，本文利用Abaqus提供的子程序接口Vumat编写用于计算湿热环境下复合材料层合板弹性响应的程序，其流程如图1所示。

图1 程序流程图

2 复合材料开孔层合板破坏极限及破坏模式的预测

2.1 开孔层合板试验

试验件结构和几何构型如图2所示，该材料单层厚度为0.115 mm。开孔拉伸试验件的铺层顺序为[45/-45/0/90/0/90/45/-45/0/90]s，层数为20层，总厚度为2.3 mm。开孔压缩试验件的铺层顺序为[45/-45/0/90/0/90/45/-45/0/90]25，层数为40层，总厚度为4.6 mm。试验件长300 mm，宽36 mm，孔径6 mm，具体几何尺寸如表1所示。

图2 开孔试验件几何构型示意图

(1) 拉伸试验

开孔拉伸试验有室温干态(25 ℃-0%RH)和干冷(-55 ℃-0%RH)两种试验环境。使用DDL-100电子万能试验机系统进行加载，如图3所示。进行破环试验时，先把载荷、位移、变形调为0，以2 mm/min的速度加载，直至试件破断，记录载荷-位移曲线、载荷-变形(应变)曲线。按照ASTM D5766规定的代码记录试验件破坏模式。

(a) 室温干态环境 (b) 干冷环境

图3 层合板开孔拉伸试验

Fig.3 Tensile test of laminates

室温干态和干冷环境下开孔拉伸试验件的破坏模式如图4所示，可以看出：其断口出现了较为明显的纤维拉断、基体拉断和分层混合破坏模式，而且两种环境下开孔拉伸试验件的破坏模式基本一致。

(a) 室温干态环境 (b) 干冷环境

图4 开孔拉伸破坏模式

Fig.4 Tensile failure mode

(2) 压缩试验

开孔压缩试验有室温干态(25 ℃-0%RH)和湿热(70 ℃-85%RH)两种试验环境。湿热试验件在试验之前放入温度为70 ℃湿度为85%的恒温恒湿箱中进行吸湿处理，试验件经过89天的吸湿后最终的平均饱和吸湿率为0.6%。

进行破坏试验时，以2 mm/min速率将载荷施加到试件上，记录载荷-位移数据。如果试件破坏，记录最大载荷、破坏载荷以及尽可能接近断裂瞬间的夹头位移，按照ASTM D6484规定的代码记录破坏模式。

室温干态和湿热环境下开孔压缩试验件的破坏模式如图5所示，可以看出：其断口出现了较为明显的纤维压缩断、基体压缩和分层混合破坏模式，而且两种环境下开孔拉伸试验件的破坏模式基本一致。

(a) 室温干态环境 (b) 湿热环境

图5 开孔压缩破坏模式

Fig.5 Compression failure mode

2.2 有限元模型

按照试件尺寸建立相应的有限元模型，如图6所示。采用C3D8R减缩积分六面体实体单元进行网格划分。边界条件为一段固支，一段通过参考点施加位移载荷，同时调用Vumat子程序进行计算，模拟湿热环境。

图6 试验件有限元模型

CF3031/BA9916-Ⅱ复合材料的工程弹性常数、材料强度属性如表2和表3所示。材料在湿热环境下性能退化常数如表4所示。

表2 室温干态下CF3031/BA9916-Ⅱ材料组分材料性能参数

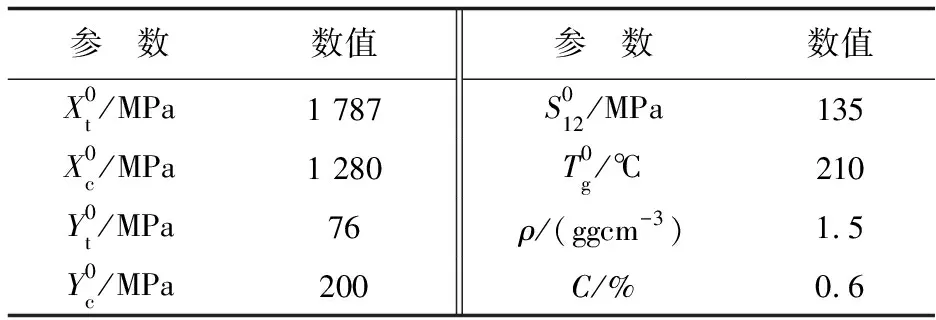
表3 室温干态下CF3031/BA9916-Ⅱ材料单向带性能参数

表4 湿热退化常数

2.3 极限强度预测

基于本文的方法对上述开孔试验件在不同温度及湿度环境下的弹性响应进行模拟。拉伸载荷作用下有限元预测结果与试验结果的对比如表5所示，压缩载荷作用下有限元预测结果与试验结果的对比如表6所示，可以看出：对于拉伸强度和压缩强度有限元预测结果与2.1节的试验结果吻合较好。有限元仿真计算得到的拉伸和压缩载荷-位移曲线如图7所示。

表5 拉伸强度仿真值与试验值对比

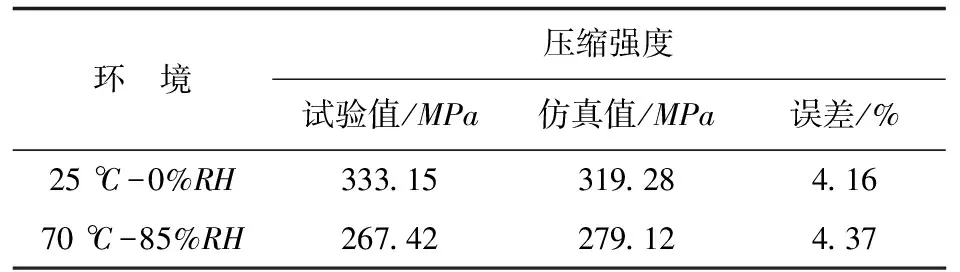
表6 压缩强度仿真值与试验值对比

(a) 拉伸

(b) 压缩

2.4 损伤扩展过程分析

图8 -55 ℃干冷条件下开孔拉伸基底拉伸损伤扩展过程

(a) 分层失效 (b) 纤维拉伸失效

Fig.9Stratifiedfailureandfibertensile

图10 层合板失效时的纤维拉伸失效单元

开孔拉伸试验件和开孔压缩试验件损伤萌生应变和初始损伤模式(如表7所示)，开孔拉伸试验件和开孔压缩试验件失效应变和最终失效模式如表8所示。

表7 损伤萌生应变和初始损伤模式

从表7～表8可以看出：湿热环境与干冷环境对复合材料开孔层合板的失效模式影响不大。在拉伸载荷作用下，层合板萌生阶段的的性能主要受环境影响较大的基体材料的影响，因此干冷状态下的萌生应变要明显大于室温干态下的萌生应变。当拉伸载荷持续增大，材料的性能主要由受环境影响较小的纤维材料的影响，因此层合板失效时的应变受环境影响不大。在压缩载荷作用下，层合板的性能主要受基体材料的影响，所以在损伤萌生阶段和破坏阶段湿热环境下的应变较室温干态下的应变都有明显下降。

综上所述，本文建立的预测模型能够较好地计算不同湿热环境下、不同载荷类型下开孔复合材料层合板的极限强度及失效模式。

3 一种基于试验与有限元模拟结果的载荷应变与环境应变的分离方法

复合材料结构实际的使用环境通常存在较大的温度与湿度变化，结构既有由载荷引起的载荷应变，又有由环境作用带来的环境应变，导致其载荷测量难以实现。解决办法之一就是对载荷应变和环境应变进行分离，本文基于以上的理论模型提出一种由实测应变得到载荷应变和环境应变的方法。

3.1 各情况单独作用下的11向应变-应力响应

本文以70 ℃-85%RH环境下开孔拉伸试验件有限元模拟结果为例分析在不同条件单独作用下层合板的应变响应，选取11向(试验加载方向)应变在0～1 000线弹性区间。三种不同组合下距离孔中心50mm处的11向应变-应力关系如图11所示。当只考虑湿热影响时，层合板的变形就是因为温度变化和吸入水分引起的热膨胀和湿膨胀的自由变形，由此变形而引起的应力-应变称之为湿热自由应力应变。其应变-应力曲线如三角实线所示，可以看到当层合板的温度由25 ℃上升至70 ℃时，由湿热膨胀产生的纵向最大应变为115，对应的最大应力为8.1MPa。当只考虑载荷作用时，即忽略湿热自由变形及湿热环境对组分材料性能的影响，其应变-应力曲线如方形虚线所示，当应变达到1 070时对应的应力为152.9MPa，可见由湿热自由膨胀引起的应力应变量相较于由机械载荷产生的应力应变是很小的。当考虑湿热力共同作用时，其应变-应力曲线如圆形实线所示，当应变达到1 106时对应的应力为136.6MPa。

图11 湿热力分别作用下的应变-应力曲线

综上所述，由湿热自由膨胀引起的11向应变只有破坏应变的3.4%(小于5%)，几乎可以忽略不计；湿热力作用下的应变-应力曲线的斜率要略大于载荷单独作用下应变-应力曲线的斜率，这是由于湿热环境使得组份材料(特别是基体材料)的性能下降，从而使层合板的总体刚度下降。

由于湿热应变分为湿热自由应变以及由湿热影响导致材料弹性模量等属性变化而带来的应变两部分，这里通过验证说明了湿热自由应变很小，可以忽略不计，但由湿热对材料弹性模量等属性带来的变化所造成的应变是不可忽略的。

3.2 载荷应变与环境应变的分离方法

对于一般的应变-应力曲线，如图12所示，湿热力作用下的应变-应力曲线可以表达为

εMHT=kMHTσ+e

(31)

式中：kMHT为湿热力共同作用下测量点11向的应变-应力曲线的斜率；εMHT为湿热力共同作用下的实测应变；e为湿热自由应变。

单独力作用下的应变-应力曲线可以表达为

εM=kMσ

(32)

式中：kM为力作用下测量点11向的应变-应力曲线的斜率；εM为力作用下的应变。

将式(31)代入式(32)，得到载荷应变εM的表达式为

(33)

环境应变εHT为

εHT=εMHT-εM

(34)

当忽略湿热自由应变带来的影响时，式(33)可以简化为

(35)

图12 一般环境下各应变-应力曲线

基于以上的理论提出一套根据实测应变和有限元模拟结果分离载荷应变和环境应变的方法。该方法主要分为以下两个步骤：

(1) 利用有限元软件分别计算得到单独力作用与湿热力共同作用下的应变-应力曲线，其斜率分别为kM和kMHT。

(2) 根据实测应变εMHT由式(35)和式(34)分别计算出该状态下对应的载荷应变εM和环境应变εHT。

70 ℃-85%RH环境下的分离湿热应变曲线(三角实线)和载荷应变曲线(圆形虚线)如图13所示。

图13 70 ℃-85%RH下应变分离曲线

从图13可以看出：载荷应变曲线与有限元预测结果(方形实线)吻合较好，验证了该载荷应变分离方法的有效性。

4 结 论

(1) 本文建立了湿热环境下复合材料层合板本构模型，并利用该模型对开孔复合材料层合板在不同温度湿度和不同受载条件下的破坏极限及失效模式进行了预测，破坏极限的预测结果与试验误差均在10%以内，失效模式的预测结果与实验结果基本一致，表明该模型是有效的。

(2) 干冷环境对复合材料层合板的拉伸强度影响较小，-55 ℃干冷环境下拉伸强度只比室温干态下提升3.43%，模型预测结果为4.29%。湿热环境对开孔复合材料层合板的压缩强度影响较大，70 ℃-85%RH环境下压缩强度比室温干态下降了19.73%，模型预测结果为12.58%。

(3) 本文基于该预测模型提出了一种在实际工程测量中分离环境应变和载荷应变的方法，该方法步骤简单易于操作，分离结果较好，为进一步研究复合材料结构件在实际使用环境下载荷测量的湿热修正提供参考。