2017-2018赛季CBA各队伍得分能力的回归分析

张志健，岳冀阳

篮球比赛是一项同场对抗类的项目，篮球比赛是通过队员之间协调配合而共同完成的，现代篮球运动的发展对球队和球员的身体素质和技战术要求日益提高，拥有良好的技术是有效战术运用的前提和基础，是提高球队整体的得分能力的必备条件[1]。本文选用比赛的技术统计指标，把2分球投球命中率、3分球投球命中率、罚球命中率、篮板球、盖帽、助攻、抢断、失误和犯规作为自变量，以球队的得分作为因变量。建立队伍得分能力的数学模型，客观地反映出影响队伍得分能力的主要因素，为运动队的实力提升提供理论基础。

1 研究对象与方法

1.1 研究对象

2017-2018赛季CBA联赛20支球队在380场常规赛中的技术统计作为研究对象。

1.2 指标设计

2017-2018赛季CBA常规赛的队伍Y(得分)、X1(2分球命中率)、X2(3分球命中率)、X3(罚球命中率)、X4(篮板球)、X5(盖帽)、X6(助攻)、X7(抢断)、X8(失误)、X9(犯规)。

1.3 研究方法

1.3.1 文献资料法

在中国篮协官网、CBA官网、虎扑体育网和贝泰科技等权威网站中，整合总决赛中双方队伍有关于得分能力的技术统计，并通过中国知网阅览大量相关篮球技战术的文献和书籍，为本文打下了十分深厚的理论基础。

1.3.2 数理统计法

从各大官方网站搜集的常规赛技术统计中，收集、整理与本研究相关的技术统计数据，采用SPSS社会统计学软件对各技术统计指标进行逐步回归处理，并在逐步回归的基础上进行分析，并用等级相关分析检验。

1.3.3 录像观察法

对2017—2018赛季38轮常规赛380场比赛现场和比赛录像进行观察，并按照比赛现场和比赛录像进行的技术统计，与官网的技术统计结合，得出最真实的数据。

2 结果与分析

2.1 比赛得分与技术指标结果

CBA是国内最大的篮球赛事，全部队伍都以夺得CBA总冠军为目标而奋斗，所以CBA比赛的对抗都十分激烈，而能够反映运动员及战术运用的指标通常包括：2分球命中率、3分球命中率、罚球命中率、篮板球、盖帽、助攻、抢断、失误和犯规。而在这么多的指标当中，不同的指标对得分能力影响的程度也不同，我们则需要运用逐步回归解决这个问题。逐步回是首先是要分别计算各自变量(X)对因变量(Y)的贡献大小，按照由大到小挑选贡献最大的一个先进入方程，随后重新计算各自变量对Y的贡献，并考察已在方程中的变量是否由于新的变量的加入而不再有统计意义[2]。如果有变量不符合入选的标准，则可以考虑剔除，直到方程里面所有的自变量都不能被剔除，方程外也没有任何变量能够被引进来，最终确定影响因变量显著的自变量的过程。2017-2018赛季CBA常规赛的20支队伍在38轮小组赛共380场比赛的技术统计(见表1)。

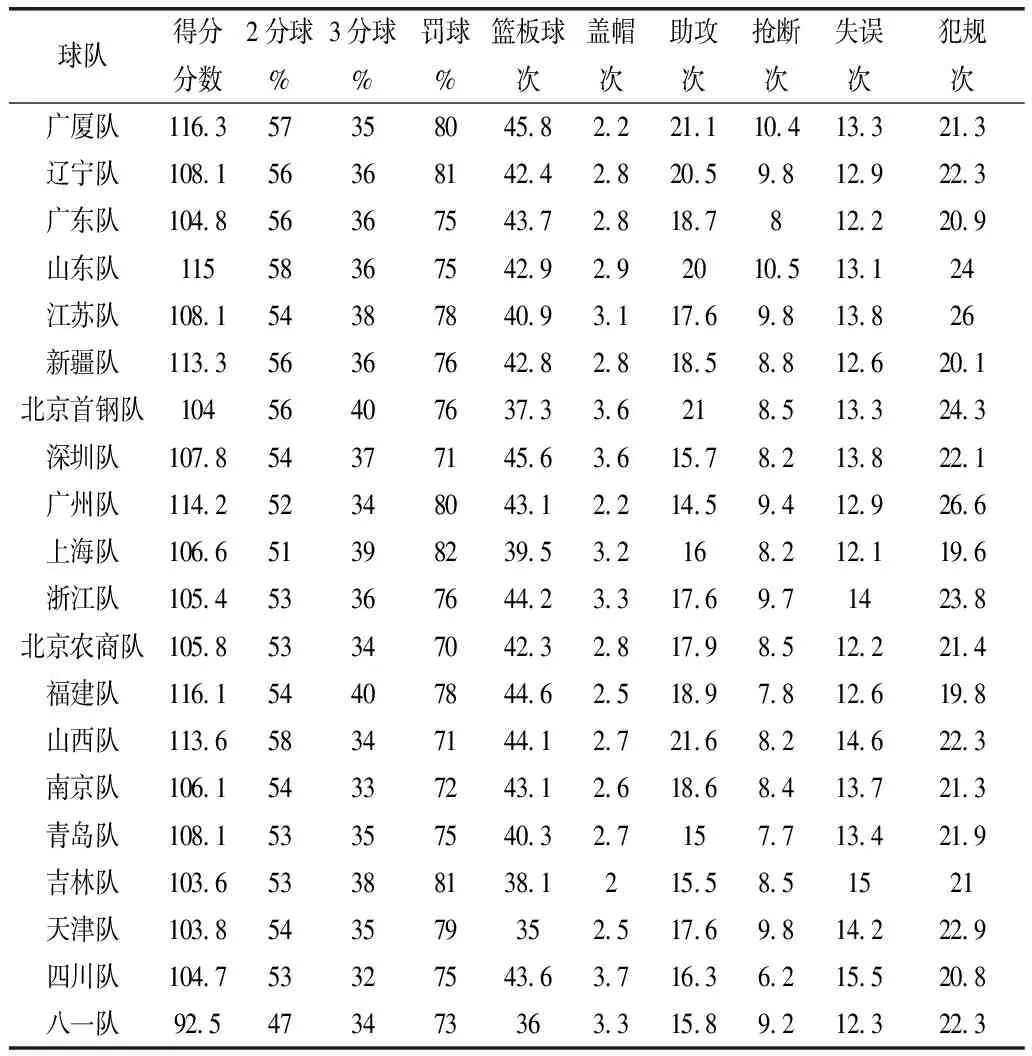
表1 2017-2018赛季各CBA队伍的技术统计

2.2 得分能力影响因素分析

篮球比赛中决定胜负的因素是得分，而各运动队的整体得分能力是综合素质的反映，为此我们以得分为因变量(Y)，其他技术统计数据为自变量(X)，进行逐步回归分析，得出因变量与自变量的关系程度。复相关系数就决定了因变量与自变量之间的关系程度，复相关系数越接近1，则因变量与自变量的关系程度越密切。CBA队伍的得分与被剔除后的自变量，复相关系数为0.844，判断系数为0.713，经过检验P<0.01，说明本研究所建立的数学模型的拟合程度相当好(见表2)。

表2 线性回归模型统计检验

注：预测变量：2分球命中率、篮板球、盖帽

从表3中可以知道，通过逐步回归分析之后，得分能力Y从9个技术统计指标中剔除了6个，他们分别是，3分球命中率、罚球命中率、助攻、抢断、失误和犯规。影响CBA各个队伍得分的主要因素分别是2分球命中率、篮板球和盖帽，每一个因素都具有显著性的意义。

表3 回归系数以及标准回归系数

注：X1、X4、X5分别表示2分球命中率、篮板球和盖帽。

标准回归系数的意义在于表明自变量与因变量之间的关系程度，标准回归系数越大，该自变量与因变量的关系程度越大。逐步回归分析的结果显示，影响因变量得分能力的程度从大到小依次是：篮板球、二分球命中率、盖帽。一个球队的前场篮板球的多少决定了这支队伍二次进攻的次数，利用外线球员的冲抢意识和预判球落点的能力、内线球员提前卡位的意识，把握每一次进攻的机会，运用前场篮板球的优势，提高二次进攻的成功率，后场篮板则直接影响队伍的节奏和攻防转换。从比赛录像可以看到，整个CBA联赛的运动员的得分基本都以2分球为主要得分手段，CBA联赛的球队中2分球命中率最高是58%，最低的也有47%，因为高强度的身体对抗是现代篮球发展的一个大方向，内外线配合的联动进攻，从而突破内线防守是球队战术的主心骨。表3可以看到，盖帽的标准回归系数为负数，这并不是表示盖帽越多，得分能力就越差。因为盖帽难度比较大，不仅仅需要身高，还需要一定的技巧，每场比赛中只有少数人能盖帽，其他人盖帽数据基本为0，只能表明少数人的得分，所以效度有所残缺，导致标准回归系数为负数。

2.3 运动队得分能力建模

逐步回归分析中剔除了6个因素后，剩下的3个因素经过方差分析对回归方程进行检验的结果显示(表4)，P值为0.000，P<0.01，说明方程有意义。

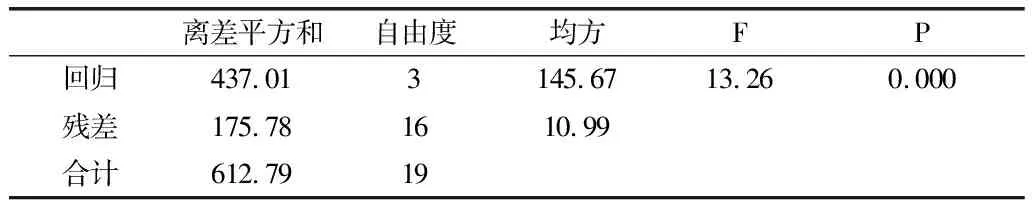
表4 方程检验表(ANOVA)

得分能力的数学模型为Y=35.73+0.88X1+0.86X4-3.88X5，该数学模型就是CBA各球队得分能力的定量表达式。要进一步证明得分能力数学模型的有效性，则得分能力必须与球队的比赛竞技排名有一定程度的相关关系。以2017-2018赛季CBA38轮380场常规赛后的积分榜排名与各CBA队伍得分能力Y的计算结果进行等级相关分析(见表5)。检验结果表示r=0.517(P<0.05)，说明积分榜排名与得分能力排名有显著性相关，积分榜排名越高，得分能力越强(见表6)。本研究建立的得分能力数学模型能反映出各个CBA球队的得分能力，因此各队教练员可以参照本研究结果，结合自己球队的优劣势，进行有针对性的训练，为提高各球队的整体得分能力提供指导依据。

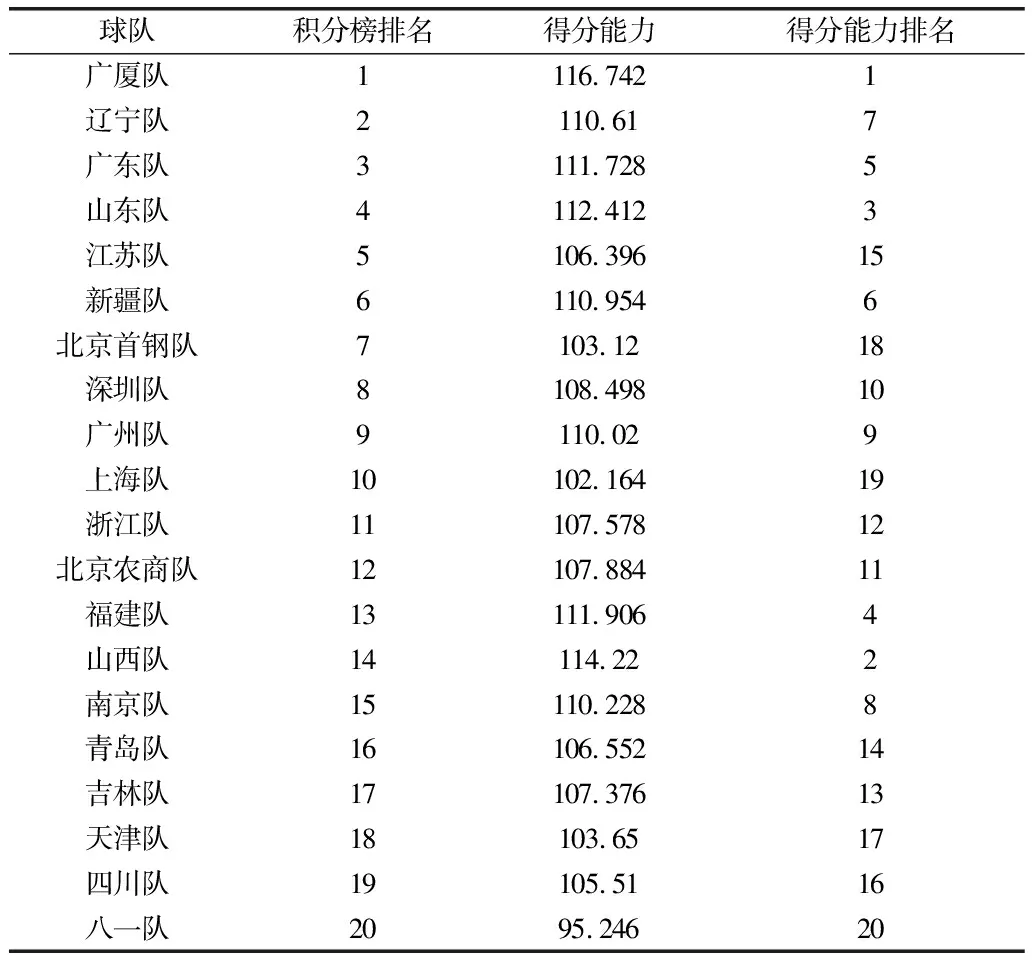
表5 各队得分能力排名与积分榜名次排序

表6 积分榜名次与得分能力排名的相关分析表

3 结论

3.1 2017-2018赛季CBA联赛中的技术统计有很多，通过逐步回归和等级相关分析后，影响得分能力的因素按影响程度从大到小依次是：篮板球、2分球命中率、盖帽。

3.2 按照逐步回归分析的结果，对队伍的得分能力建立数学模型，教练员可以根据数学模型，从技战术上的实际运用情况分析，对运动员进行有针对性的训练，从而提高整体得分能力，具有非常重要的指导意义。