苹果市场价格波动特征研究

宋晓丽　周广文　庞桂娟

[提要] 通过使用X12季节调整的乘法模型、基于HP滤波法的周期性分析并构建ARCH类模型的方法，以苹果、香蕉和橙子三类水果价格波动对比分析的视角，全面考察我国苹果市场价格波动特征。结果表明：苹果价格的季节性波动比橙子更剧烈;三类水果中，苹果价格波动周期最频繁、持续时间最短，且波动幅度最大;苹果价格不规则分量的波动幅度明显大于香蕉和橙子。基于t分布的ARCH类模型实证结果显示：苹果和香蕉价格具有明显的波动集聚性;苹果市场具有显著的“高风险、高回报”的特征;苹果和香蕉价格涨跌引发的收益率波动没有显著差异，即非对称性不显著。

关键词：价格波动;周期特征;ARCH类模型;t分布

基金项目：山东省社科规划研究项目：“山东省苹果价格波动规律、作用机理与调控政策研究”（项目编号：18CZKJ27）;泰安市社科研究项目：“泰安市农村一二三产业融合发展研究”（项目编号：18-YB-003）

中图分类号：F326.1 文献标识码：A

收录日期：2018年12月10日

一、引言

近年来，我国苹果市场价格波动剧烈，2014年10月苹果市场价格为10.03元/公斤，到2015年7月价格上涨为10.8元/公斤，涨幅7.68%，2016年3月价格又降为9.43元/公斤，下降12.69%，短期内出现剧烈且频繁的波动，供求矛盾突出。高频率大幅度的价格波动既会对果农和经销商的生产经营行为产生不利影响，又会干扰居民日常消费，扰乱正常的市场经济秩序，苹果产业的长期稳定发展受到威胁。深入分析苹果价格波动的规律，对稳定苹果市场价格、保障居民生活稳定、调动果农生产积极性有着重要的意义。

学者对我国水果市场价格波动特征进行了较多研究。对比性研究方面，对苹果、香蕉和橙子市场价格波动的特征分析认为水果价格循环周期较为稳定，对三类水果收购价格波动特征的分析认为，价格波动周期具有不可重复性和非对称性;苹果和香蕉价格波动的对比分析显示主产区价格波动强度更大;李京栋等则运用Census X12季节调整对苹果、梨和香蕉季度价格的波动周期进行了划分。针对苹果的研究方面，王俊芹等对苹果价格波动规律的研究认为苹果市场没有高风险高回报特征;而李俊青等对苹果市场价格波动的特征分析认为苹果市场具有高风险和高收益特征，其价格波动周期为15～18个月;周霞、郑艺雯对山东省苹果市场收购价格、批发价格及零售价格的变化特征规律进行了分析。

本文基于苹果、香蕉和橙子价格波动的对比分析视角，利用2002年1月至2016年3月的月度价格数据，深入考察苹果价格波动的特征规律及差异性，以期为政府稳定苹果市场价格和促进苹果产业发展提供参考。

二、苹果市场价格波动的周期特征

首先对2002年1月至2016年3月蘋果、香蕉和橙子月度价格数据运用X12季节调整的乘法模型进行季节调整，通过与两者价格波动的周期性特征进行对比分析，研究苹果价格的季节性波动、趋势变化和不规则变动特征，并利用HP滤波法对三类水果的周期性变动进行分解，深入考察苹果价格波动长期趋势及周期性特征与其他两类水果的差异性。本文价格数据均来源于中国经济与社会发展统计数据库农产品集贸市场价格。

（一）价格季节性波动特点。2002～2016年间三类水果月度价格季节因子序列的季节分布特征明显，比较而言，三类水果价格季节性波动幅度由大到小分别为香蕉、苹果和橙子，后两者价格季节性波动绝对幅度有加剧趋势。苹果价格季节性波动最高点和最低点每公斤均接近1元，而橙子价格不超过0.4元。由于香蕉不耐储存，因此其季节性波动最为剧烈，此外供给的季节性和需求全年性之间的矛盾及生产的结构性矛盾均是造成价格季节性变动的主要原因。

（二）价格趋势变化特征。对经过季节调整后的序列进行HP滤波分解，得到苹果、香蕉、橙子价格波动的趋势特征和周期特征。对趋势数据关于时间t进行多项式拟合后得到的几何效果非常理想，说明三者的价格趋势性特征明显。随着居民收入水平的提高和健康饮食意识的加强，消费结构逐渐多元化，对水果消费需求的快速增长可能是其价格稳步上涨的重要原因。比较而言，苹果价格上涨幅度最大，香蕉价格则从2014年10月开始出现下降趋势。（图1-1、图1-2）

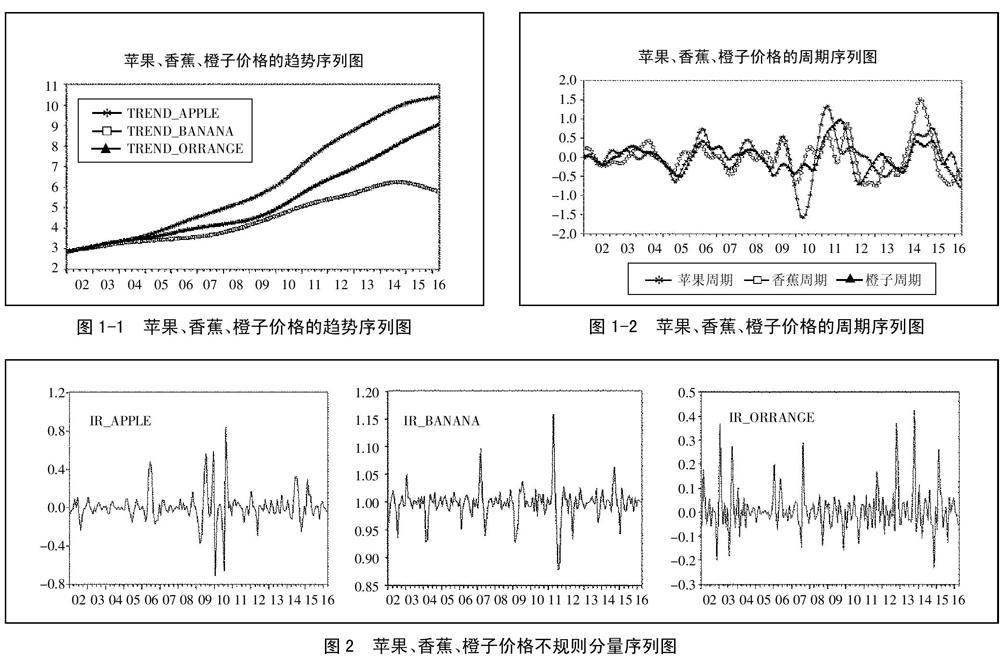
（三）价格周期性波动特征。图2显示了苹果、香蕉、橙子价格存在着明显的周期变化规律，但三类水果价格表现出不同的波动周期特征。借鉴胡友和祁春节的做法，定义某种水果的价格偏离率=价格波动值/趋势值，以判断三种水果价格波动周期性的差异。考虑实际选取每次波动偏离率所形成的波峰与波谷之间落差大于5%作为划分波动周期的标准，划分结果如表1所示。可以看到，2002年1月至2016年3月我国苹果价格经历了6次周期性波动，其中有3次较大的波动，峰谷落差超过30%，平均每21个月就会有一次价格波动;香蕉和橙子在样本期内分别发生了5次和4次周期性波动，其平均持续时长分别为31个月和40个月。通过对比发现，首先从每个波动周期的平均时长来看，苹果市场价格波动期比香蕉和橙子短得多;其次，从每个波动周期时长的变化来看，截至2007年上半年三类水果价格波动周期时长持续期较久，2007年下半年开始波动周期时长显著缩短，直到2010年年中经济逐渐复苏，苹果价格波动周期时长显著延长，而香蕉和橙子价格波动周期时长相对稳定，在样本期内没有发生较大的变化，这说明世界经济波动是影响苹果价格波动的一个重要原因，世界经济低迷可能会影响国内苹果市场价格;最后，通过对三类水果“周期长度”、“峰谷落差”两个指标的比较可以看出，苹果价格波动的若干个峰谷落差差异显著，而香蕉和橙子的峰谷落差差异较小，香蕉的峰谷落差有扩大的趋势，每个波动周期之间是不重复的和不对称的。（表1）

注：括号中的数值为z统计量;***、**、*分别表示在1%、5%、10%的显著性水平通过检验，下同

（四）价格的不规则波动特征。图2的水果价格不规则分量序列基本呈随机变动趋势，波动频繁。经过对比分析发现，苹果价格不规则分量的波动幅度明显大于香蕉和橙子。进一步的分析可以看出，2006年之前苹果价格不规则分量波动不明显，說明这期间苹果价格整体比较平稳，2006年之后苹果价格出现剧烈波动，尤其是2010年波动最为剧烈，该年份苹果价格达到谷底。可以推断，短期内水果价格出现的剧烈波动可能是由成本因素、自然灾害等一些不可观测的不规则因素造成的。（图2）

综上对比分析可以看出，与香蕉及橙子的价格波动相比，苹果价格波动除了具有明显的季节性特征和稳步上涨的趋势性特征外，苹果的价格波动周期更为频繁，周期持续时间更短，波动幅度更大，不规则分量的波动幅度也明显大于另外两种水果。

三、苹果价格波动的ARCH类模型实证分析

（一）序列平稳性检验。通过ADF方法对苹果、香蕉和橙子的价格序列进行包含趋势和常数项的平稳性检验。结果显示，三类水果价格均为非平稳时间序列。为了分析，分别引入三种水果价格的市场收益率，即：r_t=100×（lnp_t-lnp_t-1），r_t表示市场收益率，pt表示市场第t月的集贸市场价格，平稳性检验结果显示三个收益率序列在1%的显著性水平下拒绝原假设，认为他们是平稳序列。

（二）ARCH类模型建立及分析。根据市场收益率自相关图和偏相关图，同时结合AIC和SC准则，最终确定苹果和香蕉的均值方程分别为ARMA（7，1）和ARMA（6，1），橙子的均值方程为ARMA（11，1）。

苹果价格收益率选择滞后阶数为7阶时，ARCH-LM检验的F统计量在1%的显著性水平下拒绝原假设，认为残差中存在高阶ARCH效应，因此可对苹果价格收益率建立GARCH类模型。对香蕉价格收益率选择滞后阶数为1阶时，ARCH-LM检验认为残差中存在ARCH效应，应当构建ARCH类模型。橙子价格收益率选择滞后阶数为1阶时，ARCH-LM检验的F统计量在10%的显著性水平上接受原假设，即橙子收益率序列残差中不存在异方差。

通过对苹果价格收益率OLS回归后的残差项检验发现，苹果收益率的残差项不服从正态分布，具有“尖峰厚尾”非正态分布特征。如果直接假设残差服从正态分布来建模，必将会影响GARCH模型的有效性，因此本文在构建苹果收益率的GARCH模型时引入t分布和广义误差分布（GED）。对香蕉收益率残差项的检验认为其服从正态分布，因此对其构建服从正态分布的ARCH类模型，比较苹果价格和香蕉价格波动聚集性、风险性及非对称性的差异。通过EVIEWS8.0分析建立ARCH类模型，结果见表2和表3所示。

表2的估计结果显示，苹果价格收益率在残差服从不同分布假设的条件下，估计结果有较大差异。通过对AIC和SC值的比较，可以认定残差服从t分布时模型的拟合程度最好。方差方程中α₁β₁1和β₂在5%的水平下都显著，且α₁=0.36>0，说明苹果价格收益率序列存在明显的波动集聚性特征，即波动具有正相关性，大的（或小的）波动会相继出现。其次，α₁+β₁1+β₂1=0.604<1，说明过去波动冲击的影响会趋于收敛，逐渐消失。对GARCH模型的残差进行异方差检验，发现不存在异方差现象，表明在t分布下，模型能较好的拟合苹果价格序列的异方差现象。在三种不同的分布下，GARCH-M模型均值方程中，ρ的估计值都是显著大于零，说明苹果市场存在“高风险、高回报”的特征;TARCH模型的非对称项系数γ在10%的显著性水平下没有通过显著性检验，说明苹果价格波动的非对称性并不显著，价格上涨和下跌引发的收益率波动没有差异。（表2）

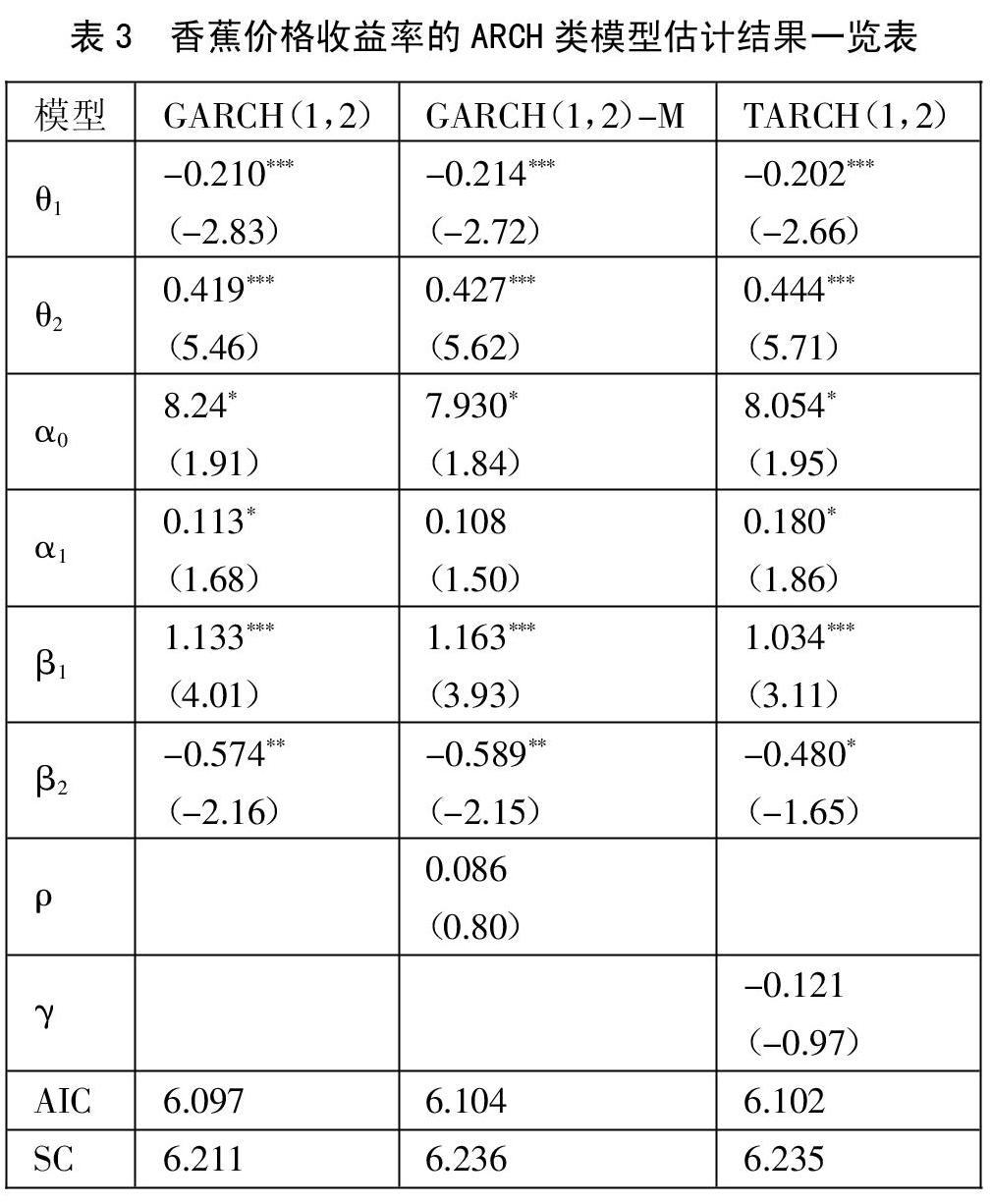
表3的估计结果显示，香蕉价格收益率的GARCH模型结果显示香蕉价格有明显的波动集聚性，过去波动的冲击对下期的影响会逐渐消失;GARCH-M模型和TARCH模型中的系数均未通过显著性检验，说明香蕉市场不存在“高风险、高回报”特征，且不存在显著的价格波动非对称性。（表3）

（三）进一步讨论。从ARCH类模型分析结果可以看出，除橙子价格序列不存在异方差外，苹果和香蕉价格收益率序列都具有明显的波动集聚性特征，大的价格波动相继出现。这种现象是由多方面的原因造成的，其主要原因可能在于我国水果市场的信息渠道不够健全，缺乏相应的价格预警机制。现阶段农户主要依靠自身判断组织种植、采摘和仓储，盲目性大，缺乏对市场需求的准确判断，导致价格波动持续发生;近些年部分地区将苹果作为精准扶贫的优势产业加以大规模推广种植，也增加了集簇波动产生的可能性。

苹果和香蕉价格未来走势受到前期价格波动的影响，并且这种影响具有很强的持续性，说明我国苹果和香蕉市场具有很强的价格记忆性。苹果市场存在“高风险、高回报”的特征，而香蕉市场不存在“高风险、高回报”特征，这可能是由于苹果一年只产一季，产量受多种因素影响，市场供给难以预测，风险较大，而香蕉生产的季节性较弱，可常年采摘，降低了市场风险。

苹果和香蕉价格的非对称性均不显著，说明价格上涨和下跌引发的收益率波动没有差异，可能是因为：当价格出现下跌迹象时，一方面由于果树种植收益通常为家庭主要收入来源，种植户难以转变现有种植结构，市场供给量变化不大;另一方面由于缺乏对未来市场价格的准确预测，种植户的仓储风险较大，往往选择全部出售，市场供给量甚至不降反升，从而导致價格下跌造成的影响相对较小;当价格出现上涨信号时，由于二者均为多年生植物，尽管价格上涨当年可能会出现扩大种植面积的现象，但由于产出滞后期较长，从而价格上涨造成的影响并不显著。

四、结论及建议

（一）结论。本文利用X12季节调整及HP滤波法对苹果市场价格变动进行分解，并建立ARCH类模型进行集聚性、高风险高回报和非对称性分析，通过与香蕉和橙子市场价格波动的分析对比，得出以下结论：（1）苹果、香蕉及橙子价格季节性特征显著，其中苹果和香蕉价格季节性波动较为剧烈;三类水果价格均呈现稳步上涨特征，具有明显的价格趋势性;苹果价格不规则分量的波动幅度明显大于香蕉和橙子。（2）三类水果价格表现出不同的波动周期特征，其中苹果价格波动周期更为频繁，持续时间更短，波动幅度更大。（3）从ARCH类模型分析结果来看，苹果和香蕉价格收益率序列具有明显的波动集聚性;苹果市场存在“高风险、高回报”的特征，而香蕉市场则不存在上述特征;苹果和香蕉价格波动的非对性均不显著。

（二）建议。根据上述结论，为平抑苹果价格波动、降低市场风险、保障种植户收益，提出以下建议：（1）总量控制，提质增效。通过政府宏观调控，有效控制苹果主产区种植面积，优化种植品种结构，提升果品质量。加大地方政府扶持力度，通过农资补贴、价格保险、灾害保险等方式，抵御价格波动风险，保障种植收益;（2）完善苹果市场信息化建设，建立有效的价格预警机制。依托信息化平台，加强水果仓储、运输和销售等信息共享，引导种植户和企业合理选择仓储量和销售时机，保障市场供求平衡，稳定市场价格;（3）充分利用苹果期货市场的价格发现功能和套期保值功能。期货价格是未来农产品现货市场的晴雨表，在市场化程度相对较高的水果市场中，期货的价格发现功能更强。适当引导种植户参与期货市场交易，既能抵御市场价格波动风险，又能保障经营收益。此外，也应当规范期货交易行为，防止期货交易的投机行为干扰期货市场相应职能的实现。

主要参考文献：

[1]李崇光，宋长鸣.蔬菜水果产品价格波动与调控政策[J].农业经济问题，2016（2）.

[2]吕建兴，祁春节.中国水果收购价格波动性研究——以苹果、香蕉和橙子为例[J].林业经济问题，2012.32（6）.

[3]王伟新，魏金义.生产空间分布是否影响水果价格波动——以苹果、香蕉为例的实证检验[J].农业现代化研究，2017.38（3）.

[4]李京栋，李先德，孙致陆.中国大宗水果价格大幅波动的影响因素分析——基于苹果、梨、香蕉价格数据[J].湖南农业大学学报（社会科学版），2018（3）.

[5]王俊芹，李宪松，王余丁.基于ARCH类模型的中国苹果价格波动分析[J].贵州农业科学，2013.41（12）.

[6]周霞，郑艺雯.基于HP滤波模型的山东省苹果价格波动特征及其影响因素分析[J].山东农业大学学报（社会科学版），2018.20（1）.

[7]胡友，祁春节.基于HP滤波模型的农产品价格波动分析——以水果为例[J].华中农业大学学报（社会科学版），2014（4）.