高中物理中的平均值问题*

王朝祥

(北京市第八十中学 北京 100102)

1 平均值的基础知识

1.1 不连续量的平均值

如果给出一系列数值x1，x2，x3，…，xn，xn>0，以不同的数学运算方式可以取得不同类型的平均值.

算术平均值

几何平均值

调和平均值

方均根

加权平均值

W=x1p1+x2p2+…+xnpn

其中加权系数之和

p1+p2+…+pn=1

不同平均值之间的大小关系：H≤G≤A≤R，当x1=x2=x3=…=xn时取等号．

1.2 连续函数的平均值

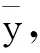
如图1所示，其几何意义为：在区间[x1,x2]范围内，函数曲线下所围曲边梯形的面积等于矩形ABCD的面积，矩形的高即为函数的平均值．

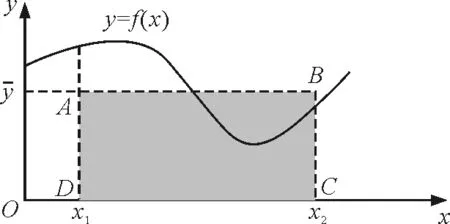
图1 y-x图像

若将积分区间分成n个等份(n→∞)，每一份记为Δx，对应的函数值为yi，则

由此可见，连续函数的平均值与不连续量的算数平均值在本质上是一致的．

2 平均值在物理中的应用

2.1 平均值问题中的等效替代思想

物理学需要研究各种变量，许多物理量的变化过程是非均匀的，研究起来比较困难．引入平均的思想，可以用一个等效的常量代替变量，或者用一个均匀的变化过程代替非均匀的变化过程，从而对大量的同类变量或非均匀变化的过程做出整体的、概括性的描述．不同平均值的数学运算方式不同，其物理意义也不同．

在测定性的物理实验中，对待测物理量进行多次测量，然后把各次的测量结果取算术平均值，以此作为待测物理量的测量值，可以有效地减小实验过程中的偶然误差．

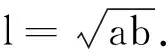
如果某个物理量的平均值跟参与平均的各个量在总体中的权重有关，就要用到加权平均值．例如单向直线运动的平均速度、混合物的密度(不考虑总体积变化)、混合物的比热容、混合物的平均摩尔质量、质心坐标，等等．作为特例，如果各个量的权重相同，加权平均值就等于算术平均值．

调和平均值H是各个量倒数的算术平均值的倒数，在中学物理里有几种典型应用．例如：电路中有n个不同的电阻R1，R2，…，Rn并联，从对电流的阻碍作用来看，这些电阻可以等效地看作n个相同的电阻Rh并联，Rh即为这n个电阻阻值的调和平均值；电容器的串联也有类似的规律．

温度是分子热运动剧烈程度的标志，温度越高，分子平均动能越大．分子平均平动动能是各个分子平动动能的平均值，即

有定积分作为数学工具，计算连续函数的平均值就不再困难．例如，力的空间累积是功，力对位移的平均值可以表述为

借助力对位移的平均值，可以将变力做功问题等效地转化为恒力做功问题．类似的平均值问题还有力对时间的平均值、平均速度、平均加速度、平均电流、平均功率等．

交变电流的有效值是根据电流的热效应定义的，即如果交变电流i(t)一个周期T内在电阻R上产生的热量与某一恒定电流I相同时间内在电阻R上产生的热量相等，恒定电流I称作交变电流i(t)的有效值．即

有效值

例如，正弦交流电i(t)=Imsin(ωt+φ)的有效值

借助微元思想可以体会，交变电流的有效值I实际上是一个周期内电流的方均根．

2.2 应用平均值时要注意的几个问题

物理量的各种平均值具有丰富的物理意义，计算物理量的平均值时要注意平均的对象、平均的区域、平均的方法这3个问题．

平均值的计算都有具体的对象．同一个物理量，若所取的平均对象不同，计算所得的平均值也就不同．辨别平均的对象，解决的是“对什么取平均”的问题．例如，力对位移的平均值等于该力所做的功与所对应位移的比值，力对时间的平均值等于该力的冲量与所对应时间的比值，这两个平均值具有不同的物理意义．

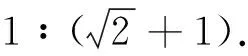
不同类型的平均值所对应的数学运算方法不同，其物理意义也就不同．计算平均值时，要根据具体的物理情景和物理问题的需求，选取不同的平均方法．

3 典型问题分析

【例1】某物体做匀加速直线运动，在一段时间内其速度由v1增加到v2，求该物体在这段时间内的平均速度及其在位移中点的瞬时速度．

解析：物体的加速度记为a，加速时间

位移

其平均速度

联立解得，物体在位移中点的瞬时速度

点拨：在匀加速直线运动中，中间时刻的瞬时速度(平均速度)等于始末速度的算术平均值，位移中点的瞬时速度等于始末速度的方均根．

若将物体做直线运动的位移分为相等的两段，前半段的平均速度为v1，后半段的平均速度为v2，则全程的平均速度

此为v1和v2的调和平均值．

另外，若将物体的直线运动分为前后两段，第一段运动的时间和平均速度分别为t1和v1，第二段运动的时间和平均速度分别为t2和v2，则全程的平均速度

此为v1和v2的加权平均值．

请读者结合本题中4种平均速度的计算，体会不同类型的平均值在物理意义上的区别．

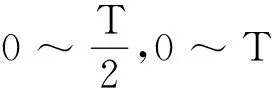
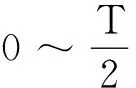
在0～T时间内

点拨：本题中，电流对时间的平均值与时间段(平均的区域)的选取有关．

不同的物理过程内，物理量的平均值一般不同．因此，叙述物理量的平均值时要明确所对应的物理过程．

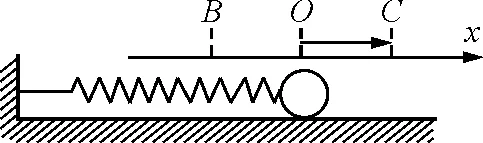
图2 例3题图

解析：弹力与位移的函数关系为F=-κx，此过程中弹力对位移的平均值

弹力与时间的函数关系为

F=-κAsinωt

此过程中弹力对时间的平均值

【例4】在一次实验中，某同学用螺旋测微器测量某圆柱体的直径D，在柱体的不同位置测量了6次，测量结果如表1所示.

表1 直径D的测量值

请计算直径的算术平均值及其标准差．

解析：测量结果的算术平均值

1.048 0+1.049 5+1.047 0)=1.049 18 cm

测量值的不确定度

算术平均值的标准差

所以，直径的测量结果可以表述为

点拨：在处理实验数据的过程中，测量结果不确定度的估算涉及方均根的运算．表述测量结果时，测量结果的有效数字与不确定度的最后一位对齐．