基于可重随机化混淆电路的可验证计算∗

赵青松,曾庆凯,刘西蒙,徐焕良

1(计算机软件新技术国家重点实验室(南京大学),江苏 南京 210023)

2(南京大学 计算机科学与技术系,江苏 南京 210023)

3(福州大学 数学与计算机科学学院,福建 福州 350117)

4(School of Information Systems,Singapore Management University,Singapore 178902,Singapore)

5(南京农业大学 信息科技学院,江苏 南京 210095)

1 引 言

可验证计算可使计算能力较弱的客户端将函数计算外包给计算能力强但不被信任的服务器,服务器返回计算结果以及计算正确执行的证据,并要求客户端验证此证据的开支必须比自己重新计算函数的开支要小.另外,可验证计算也需要保证隐私性,即服务器对客户端输入(也可以包括输出)一无所知.Kilian在早期关于有效论证(argument)[1]和Micali的计算正确证明(computationally sound proof,简称CS Proof)[2]中都提出了计算双方交互只有1轮的非交互可验证计算.Gennaro等人形式化定义和构造了客户端和服务器之间的非交互可验证计算方案[3].随后,在非交互可验证计算方面的许多工作也提出了很多安全外包任意函数的密码方案[4-12].

Yao的混淆电路(Yao’s garbled circuit)是一种实现半诚实敌手下的安全两方计算经典和有效的手段[13,14],但是混淆电路存在电路只能使用 1次的基本限制,为电路提供超过 1次的编码输入会损害混淆电路的保密性.Goldwasser等人采用全同态加密(fully homomorphic encryption,简称FHE)的方法首次构造了用于两方计算的可重用混淆电路.困难性假设是误差学习(learning with error,简称LWE)假设,不过,该构造只达到选择(selective)安全[15].Agrawal也采用 FHE基于 LWE假设构造安全性更强的半适应性(semi-adaptive)安全可重用混淆电路[16].在可验证计算背景下,客户端可以采用Yao的混淆电路将只有客户端输入的函数外包给不信任的服务器.但是,用于可验证计算的混淆电路也存在电路只能使用一次的基本限制.组合使用FHE和混淆电路可使客户端和服务器实现多项式次数输入的混淆电路重用[3].然而,该方案只在敌手不能对客户端发起任何数量的验证查询(verification query)这种较弱的模型下被证明是安全的.同样地,为了满足安全的需要,许多其他的可验证计算解决方案也是依赖于FHE的[5,7,9,10].

尽管理论上基于 FHE的可验证计算是可能的,但实际上因为所用的 FHE方案效率十分低下[17],所以基于FHE的可验证计算构造实际运行开支都很高,且通常需客户端和服务器都执行 FHE,这对于计算能力较弱的客户端,甚至对于计算能力强大的服务器来说,都是很重的负担.

采用密码方法解决可验证计算都需要特定的密码困难性假设.Brakerski等人提出了基于LWE假设的限层全同态加密(leveled fully homomorphic encryption)[18],这是基于格的公钥加密最好的已知困难性假设.但是,所有标准(非限层)FHE的假设都需要更强的环安全(circular security)假设.因此,我们有兴趣构造可验证计算协议,使其所基于的困难性假设尽可能地弱,这样,如果其中的原语(primitive)被证明对新的攻击是脆弱的,或者新出现的原语具有更好的性能,那么协议所使用的原语就要被替换.

1.1 本文贡献

在本文中,我们将首先构造一个采用加同态加密的非交互可验证计算协议.它是基于 DDH假设,在任意新输入下能够实现客户端基于混淆电路的外包计算,可以容忍多项式次数的恶意验证查询,并为提供客户端的输入输出隐私保护,以及函数计算的正确性和语义的安全性.

客户端可使用 Yao的混淆电路,将只有客户端输入的函数计算外包给服务器,但在新输入下重用电路是不安全的.这是因为电路的输出标签一旦泄露,服务器就可能使用这些标签作为下次外包计算的结果输出.本文解决这个问题的主要方法是可重随机化的混淆电路(re-randomizable garbled circuit),其可实现客户端使用随机数r产生的混淆电路,以及服务器根据此混淆电路和客户端给定的随机数r′(affine transformations,也就是映射转换)产生的重随机化混淆电路(re-randomized garbled circuit),计算能力有限的敌手将不能区分它们[19,20],这意味着原混淆电路和重随机化电路的分布是计算上不可区分的.

然而,由于以下两个因素,可重随机化的混淆电路并不能直接用于可验证计算.

· 首先,服务器产生重随机化混淆电路之后,客户端将函数输入重随机化后发给服务器,服务器就可以根据此重随机化输入逐个门电路(gate by gate)检查重随机化混淆电路,最终得到重随机化的输出.但是,由客户端给定的映射转换和重随机化输入,服务器会获取原混淆电路的有价值信息.

· 其次,重随机化混淆电路的构造过程仅在半诚实模型下是安全的,易受到来自行为可以表现为任何方式的恶意敌手攻击.例如,如果一个恶意的服务器使用同样的映射转换重复重随机化混淆电路,服务器就有可能使用重随机化混淆电路超过1次.

重随机化混淆电路过程的有效性证明是典型的零知识(或证据不可区分)证明.一般地,可以使用随机预言机模式经 Fiat-Shamir范式获取有效的非交互零知识证明[11,20].为了优化针对恶意敌手的协议,本文将采用第 3节的方法,不使用Fiat-Shamir范式,实现恶意敌手下的安全重随机化混淆电路,从而使协议更简洁.

为了能够将可重随机化的混淆电路应用于可验证计算,采用的主要技术手段是数学隐藏方法(mathematical disguise method)[21]和Kilian的随机化技术(Kilian’s randomization technique)[22].数学隐藏方法使服务器在重复随机化混淆电路过程中不能重用映射转换,以及客户端的开销与函数的计算开支无关.Kilian的随机化技术随机隐藏映射转换的每个部分,从而确保服务器按序重随机化电路.该技术手段可以抵御混合输入攻击(mixedinput attack)和部分计算攻击(partial evaluation attack).此外,由于上述可验证计算协议是静态(static)安全的,因此,我们还给出了该协议实现适应性(adaptive)安全的方法.

在本文的最后部分,将上述构造应用于密码转置防火墙(cryptographic reverse firewall)[23],给出一种不采用FHE安全两方计算下的混淆电路重用方法.密码转置防火墙可被解释为一种状态算法,该算法能够处理安装防火墙的用户发送和接收的已由某些密码算法处理的消息.一方面,如果原有实现已被破坏,则密码转置防火墙将恢复其安全性;另一方面,如果原有实现是正确的,但密码转置防火墙是不安全的,此时密码转置防火墙并不比任何主动敌手更具破坏性.例如,利用某些特定的协议性质,它能够挂起拒绝服务攻击,如丢掉一些消息.从这个角度来说,不必比传播媒介更信任密码转置防火墙.

密码转置防火墙的关键技术是可重随机化的不经意传输(re-randomizable oblivious transfer)和可重随机化的混淆电路.然而,密码转置防火墙重随机化混淆电路超过1次是不安全的.为了打破该局限,也是作为上述构造的一个应用,本文提出一种新的密码转置防火墙模型——可重用密码转置防火墙,用户生成混淆电路 1次,然后可重用转置密码防火墙可安全的重随机化混淆电路多次.

2 预备知识

2.1 可验证计算定义

遵循文献[3,10],下面介绍非交互可验证计算定义.假设客户端将函数f计算外包给服务器,然后服务器返回计算结果和计算正确执行的证据.可验证计算方案VC的形式化描述由以下4种算法组成.

·KeyGen(1,f)→(pk,sk).随机化密码生成算法将安全参数和函数f作为输入,生成公钥pk和私钥sk,客户端将公钥发送给服务器,私钥由客户端秘密保存.

·ProbGen(sk,x)→(σx,τx).问题生成算法将密钥sk和客户端的函数输入x作为输入,输出x的编码输入σx和秘密值τx.σx由客户端发送给服务器用于计算,τx由客户端用于验证.

·Compute(pk,σx)→(σy):给定公钥pk和编码输入σx,服务器运行该算法计算函数f输出y=f(x)的编码形式σy.

·Verify(sk,σy,τx)→(acc,y).输入密钥sk和秘密值τx,客户端执行验证算法.该算法将服务器的编码输出σy转换成一个比特acc和一个字符串y.如果acc=1,客户端就接受计算结果y=f(x);如果acc=0,客户端就拒绝接受计算结果.

若恶意的服务器输入由算法ProbGen生成的σx,执行算法Compute产生的结果不能被验证成功且与函数f在输入x的计算结果不一致,则该可验证计算方案VC是正确的.

定义1(正确性).∀x∈Domain(f),∀f∈F,其中,F是一个函数族,若(pk,sk)←KeyGen(1,f),(σx,τx)←ProbGen(sk,x),(σy)←Compute(pk,σx),则(1,y=f(x))←Verify(sk,σy,τx)以不可忽略的概率成立,那么该可验证计算方案VC是正确的.

若敌手不能使验证算法接受一个不正确的输出,则可验证计算方案VC是安全的.也就是说,对于函数f和输入x,若,则Verify不能输出.

考虑关于敌对的服务器A的如下实验.

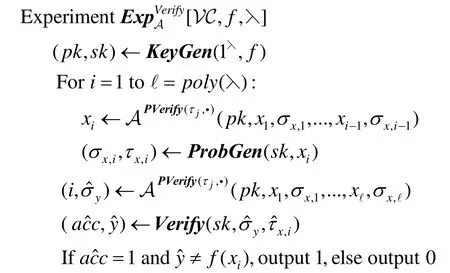
其中,预言机PVerify(σ,τ)返回acc,当且仅当表示敌手A的 PVerify 查询.

上述实验中,敌手通过访问预言机生成多个问题实例,并检查客户端对任意编码的响应.若给定一个输入值,敌手产生输出使验证算法接受该错误的输出值,则敌手成功.

定义2(安全性).为可验证计算方案VC定义敌手A,其在上述实验中的优势为

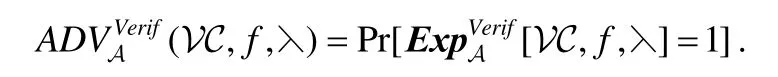
输入(输出)隐私的定义采用不可区分方法以确保没有输入(输出)信息泄露.由输入隐私立即得到输出隐私.若有两个不同的输入,问题生成算法ProbGen产生的两个输出是计算上不可区分的,则可验证计算方案VC是隐私的.实验定义如下.

其中,预言机PProbGen(x)表示调用ProbGen(sk,x)生成(σx,τx),且仅返回表示敌手A的 PProbGen查询.

定义3(隐私性).为可验证计算方案VC定义敌手A,其在上述实验中的优势为

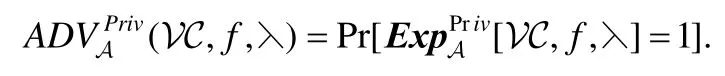
若对任意的f∈F和任意的概率多项式时间敌手可以忽略不计是成立的,则可验证计算VC是隐私的.

在外包函数f的每次计算过程中,客户端执行的算法ProbGen和Verify共同复杂度要比函数f的复杂度要小,其中未考虑复杂度为poly(|f|)的算法KeyGen.原因是由于考虑的是摊销复杂度模式,即为了提高在线阶段效率,客户端需在离线阶段付出大量的计算开销(和函数f的复杂度相同).

定义4(效率).∀x∈Domain(f),∀f∈F,其中,F是一个函数族,若算法ProbGen和算法Verify共同运行时间是o(T),其中,T是计算函数f所需时间,则可验证计算方案VC是有效率的.

2.2 BHHO加密算法

BHHO加密算法是一个基于DDH假设的公钥加密算法[24].定义q是群G的阶,g是群G的生成元,ℓ=「3logq.该公钥加密算法PKE由以下3种算法组成.

·Gen(1).从群G和{0,1}ℓ中分别一致随机选择向量(g1,...,gℓ)和比特串s=(s1,...,sℓ),计算h=、密钥sk=s、公钥.

·Enc(pk,m).随机选择r←Zq.群元素m∈G加密后的密文形式为.

·Dec(sk,c).密文.算法输出.

BHHO 算法的密钥和明文都具有加同态性质.定义f(x)=Ax+b为从到的可转置映射转换(invertible affine transformation,简称 IAT).若M-1(x⊤|1)⊤=(f(x)⊤|1)⊤,则定义M为f(x)的逆映射转换(reverse affine transformation,简称 RAT).若给定 BHHO公钥pk和密钥sk,加密比特p的密文为,则设密钥sk′=f(sk)∈是0-1向量,那么pk·M是sk′的公钥,c·M是关于pk·M同样比特p的密文.明文具有同样的同态性质.对于密钥同态,因为在计算过程中用到了转置运算,所以映射转换必须是可转置的.而对于明文同态,任意的映射转换都可以.

2.3 混淆电路

本节介绍混淆电路的构造,采用 Yao原有构造方法[13,14,19]的表达方式.在半诚实模式下的安全两方计算中,有一对参与方 Alice和 Bob有各自的输入,组合使用混淆电路和不经意传输可实现安全计算函数.与此不同的是,在可验证计算中,只有客户端有私有的输入.

设有一系列具有n-bit输入的布尔电路{Cn}n∈N,对于电路C∈{Cn}n∈N中电线w,客户端随机选择两个ℓ-bit标签,分别表示电线w的输入比特为0和1,其中,ℓ是BHHO的密钥长度.给定输入电线分别是a和b,输出电线为c的门电路g,为其随机选择4个新2ℓ-bit的掩码(mask)δi,j,其中i,j∈{0,1},计算如下4个密文对:

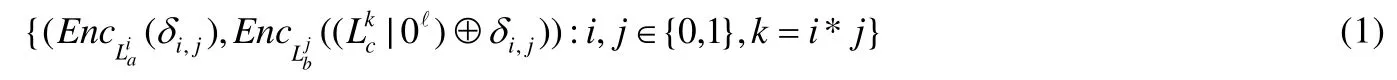
其中,操作符*表示门电路的相应操作.客户端使用 BHHO密钥加密掩码δi,j,使用另一个 BHHO密钥加密经过与掩码异或的标签(与ℓ-bit 0连接).4个密文对随机排序以混淆电路结构.密钥(也就是电线标签)由客户端秘密存放.在电路计算过程中,客户端将整个混淆电路Γ和输入电线的标签(也就是客户端输入x∈{0,1}n相应的编码c)发送给服务器,服务器逐门电路检查电路,对于门电路g,服务器获知两根输入电线标签La和Lb,用La解密每个密文对的前半部分,用Lb解密其后半部分,并异或它们,如得到形式,就取其前半部分Lc作为门电路输出.最后,服务器计算所有的电路输出电线标签并发送给客户端.

定义5(混淆电路).{Cn}n∈N表示一系列具有n-bit输入的布尔电路,电路的混淆电路方案Gb由以下3个过程组成.

·Gb.Garble(1,C)→(Γ,gsk):获取电路C,输出混淆电路Γ和密钥gsk.

·Gb.Enc(gsk,c)→c:获取输入x和密钥gsk,输出编码c.

·Gb.Eval(Γ,c)→y:获取混淆电路Γ和c,计算输出y.

定义6(混淆电路的正确性).对每个安全参数,,所有的x∈{0,1}n:

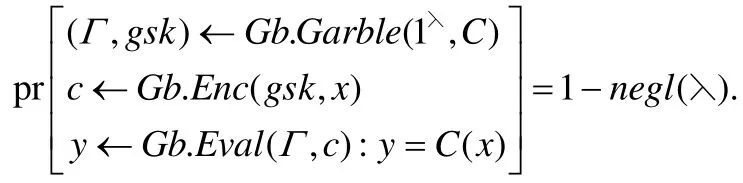
定义7(静态安全).混淆电路是静态安全的,如果存在PPT模拟器S,对任意PPT敌手A:

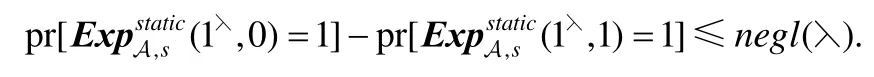
1.挑战者随机选择比特b.

2.敌手A向挑战者提交C和x.

“三严三实”专题教育要求突出问题导向，着力解决一部分领导干部中存在的理想信念动摇、信仰迷茫、精神迷失，宗旨意识淡薄、忽视群众利益、漠视群众疾苦，党性修养缺失、不讲党的原则等问题；着力解决一部分领导干部中滥用权力、设租寻租，官商勾结、利益输送，不直面问题、不负责任、不敢担当，顶风违纪还在搞“四风”(即形式主义、官僚主义、享乐主义、奢靡之风)，不收敛不收手等问题；着力解决一部分领导干部中无视党的政治纪律和政治规矩，对党不忠诚、做人不老实，阳奉阴违、自行其是，心中无党纪、眼里无国法等问题。

3.如果b=0,则挑战者生成和,返回和.

4.如果b=1,则挑战者生成和,其中,T(C)揭露C的拓扑结构,返回和.

5.最后,敌手A输出猜测比特b′,如果b′=b,则敌手A获胜.

定义8(适应性安全).混淆电路是适应性安全的,如果存在PPT模拟器S,则对任意PPT敌手A:

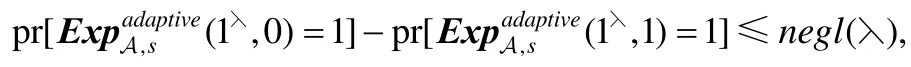
1.挑战者随机选择比特b.

2.敌手A向挑战者提交C,挑战者返回.如果b=0,则挑战者生成;如果b=1,则挑战者生成,其中,T(C)揭露C的拓扑结构.

4.最后,敌手A输出猜测比特b′,如果b′=b,则敌手A获胜.

2.4 可重随机化的混淆电路

Gentry等人为实现”i-hop”同态加密方案,构造了基于DDH假设的可重随机化的混淆电路[19,20],利用BHHO的同态性质实现电路的重随机化,将密钥和明文看作向量,它们是关于Zq任意映射函数的同态(我们定义映射函数为与置换矩阵(permutation matrix)相乘).通过两个随机置换π,π′,可将密文EncL(L′)转换成.对于输入电线分别是a和b、输出电线为c的门电路g,等式(1)定义了它的4个密文对.RATπa,πb,πc分别是与a,b,c相对应的[ℓ+1]上的随机比特序列,采用BHHO密钥同态和明文同态性质将等式(1)的4个密文对转换为

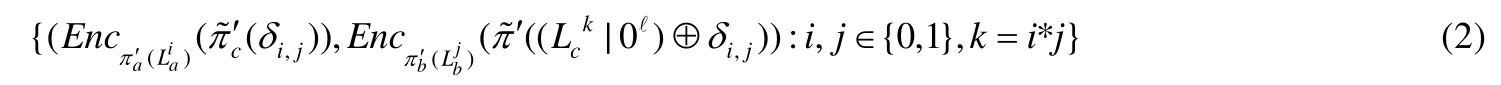
定义9(可重随机化的混淆电路).是[ℓ+1]上的随机比特序列 RAT,混淆电路Γ的可重随机化混淆电路方案由如下3个过程组成:reRandGb={reRandGb.Gate,reRandGb.InLabel,reRandGb.OutLabel}.

3 技术概述

文献[19]中构造了基于BHHO加密算法(详见第2.2节)的可重随机化混淆电路.在本文中,需要服务器利用BHHO算法的同态性质和可重随机化性安全重复重随机化来自客户端的混淆电路.具体来说,给定输入电线分别是a和b,输出电线为c的门电路g(用4个密文对表示),客户端选择3个与电线a,b,c分别对应的RATπa,πb,πc,以及4个随机掩码,其中,i,j∈{0,1},将它们发送给服务器(我们定义RAT为与一个置换矩阵的乘积运算,IAT也类似).接下来,服务器将每个密文对的前半部分与πa,πb分别相乘,后半部分与πb,πc分别相乘,并且将 4个掩码与此时的4个密文对分别做异或运算.但是,服务器直接使用RATπa,πb,πc重随机化门电路会导致混淆电路重用变得不再安全.重随机化标签的方法是从混淆电路的电线标签L和其IATπ′入手,将π′应用于L,也就是π′(L),而π′又可以从随机的 RAT获得.于是,服务器在逐个门电路检查重随机化电路时,就能从π′和π′(L)中提取标签L.在环安全中,模拟器已知RAT但不知重随机化的密钥[24].

我们的想法是限制服务器明确地获知RAT或 IAT,解决方案是使用数学隐藏方法[21]和 Kilian的随机化技术[22].数学隐藏方法可将每个RAT表达为3个矩阵的乘法链,Kilian的随机化技术可将其中的每个矩阵前乘和后乘可转置随机矩阵.例如,设某个RAT为可转置随机矩阵A,表示为3个矩阵B,C,D乘法链,选取可转置随机矩阵R1,R2,将3个矩阵分别表示为随机化形式:,其中,R0是单位矩阵,它们相乘即可恢复矩阵A.

客户端的随机化密钥生成算法 KeyGen为混淆电路的门电路i一致选取可转置随机矩阵,为混淆电路随机选取随机矩阵,且构建矩阵(由服务器为门电路选取掩码对电路的安全性没有影响).接下来,在每次外包计算中,客户端的问题生成算法 ProbGen也为混淆电路选取可转置随机矩阵,构造 3个矩阵,其中,R0是大小合适的单位矩阵.接下来,服务器执行算法 Compute为门电路i计算矩阵链乘:

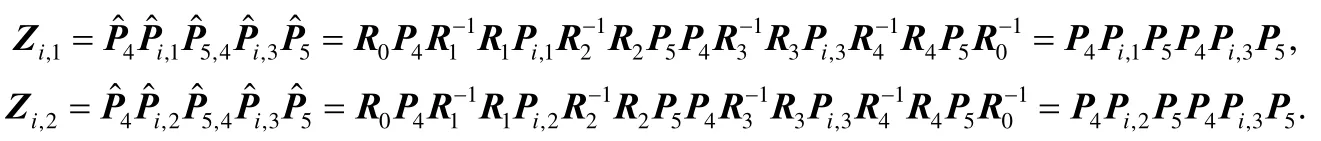
其中,P分别是门电路i的两个输入电路和输出电线的被用于随机化门电路i,上述过程并没有将RAT泄露给服务器.重随机化前后的门电路如图1所示,重随机化多个门电路如图2所示.这时,门电路1的输出电线是门电路2的输入电线之一,它们具有一致的重随机化状态和同样的RAT.

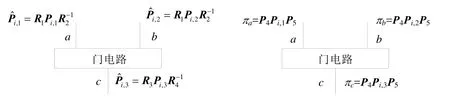
Fig.1 A gate that will be re-randomized and the re-randomized gate图1 重随机化前的门电路和重随机化后的门电路

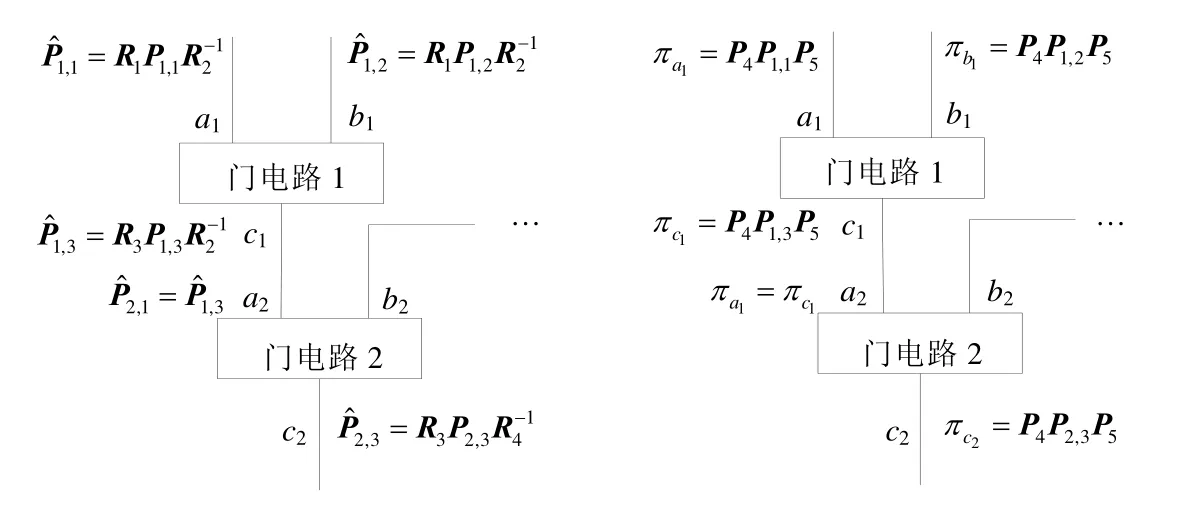
Fig.2 Two gates that will be re-randomized and the re-randomized gates图2 重随机化多个门电路前后状态

给定电路输入电线的IAT(从RATP4Pi,1P5和P4Pi,2P5易得),客户端的问题生成算法ProbGen利用BHHO加密算法的密钥同态重随机化输入标签.根据这些重随机化标签和重随机化电路,服务器利用Compute算法逐门电路检查重随机化电路,得到中间以及电路输出门电路由IAT随机化的标签.

输出的正确性要求服务器将正确输出交付给客户端,若根本什么都没有交付,则服务器被认为是欺骗或计算错误.Gennaro等人指出,如果通过检查重随机化混淆电路恢复出正确的电路输出电线标签,则足够表明服务器的电路重随机化过程是诚实的(可参考第 2.3节)[3].另外,我们的方案还能容忍服务器发起任意次数的验证查询.也就是说,服务器能够获知客户端是否接受或拒绝计算结果.在验证查询下安全的原因是,客户端接受或拒绝决定的比特只与混淆电路的重随机化过程计算相关.

4 可验证计算协议

4.1 协议形式化描述

高层次上的协议描述如下所述.

· 在离线阶段,客户端将函数的混淆电路形式和所有门电路的矩阵(Kilian的随机化技术隐藏的映射转换固定部分)发送给服务器.

可验证计算协议构造如下所示.

·KeyGen(1,f)→(pk,sk).将f表示为电路C.该算法由客户端执行如下步骤.

➢ 首先,运行混淆电路生成算法产生电路C的混淆电路,混淆电路电线i标签记为.具体来说,执行,其中,Γ为混淆电路,是电路输入电线标签,是电路输出电线标签.对于门电路i,j∈[|Γ|],随机选择可逆矩阵和4个门电路随机掩码,为混淆电路也随机选择可逆矩阵:

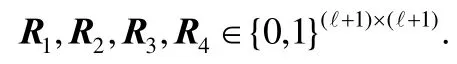
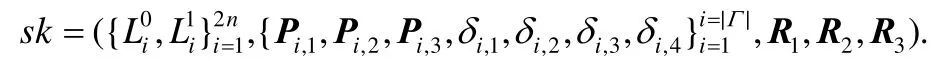
·ProbGen(sk,x)→(σx,τx).定义输入x为n比特大小,即x=x1,…,xn.为混淆电路随机选择可逆矩阵P4,P5∈,构造矩阵,其中,R0是大小合适的单位矩阵.执行,生成输入编码c.对输入标签i∈[n],计算:

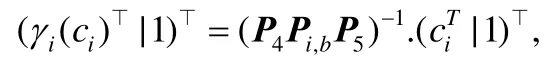
其中,b∈{1,2},γi(ci)表示重随机化输入标签.电路输出电线的 IATη1,…,ηn也可通过类似计算得到.

·Compute(pk,σx)→(σy).解析σx,对每个i∈[|Γ|],计算,并选择4个随机掩码.运行.计算,.输出σy=(e1,…,en).

·Verify(sk,σy,τx)→(acc,y).解析σy为e1,…,en.如果对输出标签i∈[n],等式Li=reRandGb.OutLabel(ηi,ei)成立,则acc=1(接收);否则,acc=0(拒绝).如果acc=1,则利用密钥sk将ei映射为输出y;否则,输出⊥.

协议的正确性可由混淆电路、可重随机化的混淆电路,数学伪装方法和Kilian的随机化技术的正确性直接得出.BHHO加密算法确保了输入和输出隐私,而随机矩阵链乘使得映射转换也是隐私的,对服务器隐藏的原混淆电路可实现输入和输出隐私的电路重用(见定理2).协议的离线阶段(执行KeyGen)代价为O(poly()|C|),与函数f相关而与被委托输入无关,其中,|C|是函数f电路的大小.每次外包计算中,客户端外包计算在线的代价是O(poly()·n)(执行 ProbGen),计算 3 个矩阵链乘代价是O(1),执行 Verify 的代价是O(poly()·n),因为在线代价与函数f的电路大小无关,所以该方案是非平凡的(non-trivial).也就是说,客户端自己计算函数f的开支比在线代价要大.服务器在线阶段的代价是O(poly()|C|)(执行Compute).

文献[3]中具有预见性的方案虽然类似于上述可验证计算协议,但是需要强调与之不同的几点.

· Gennaro等人给出的可验证计算方案只在敌手不能对客户端发起任何数量的验证查询这种较弱的模型下被证明是安全的.我们的方案能够容忍多项式次数的恶意验证查询.

· Gennaro等人组合使用Yao的混淆电路和FHE实现安全的多项式次数输入的混淆电路重用,输入比特相应的标签使用FHE加密.为实现多项式次数输入的混淆电路重用,我们使用BHHO加密算法的加同态性质重随机化标签和混淆电路.

· Gennaro等人仅考虑客户端将任意函数计算外包给不被信任的服务器这种非交互可验证计算模式,我们不仅考虑可验证计算,而且也考虑了两方计算下的私有函数计算(private function evaluation,简称PFE)协议(详见第5节).

· 我们的方案是基于DDH假设,比Gennaro等的方案速度更快、更加紧凑.

4.2 安全分析

利用数学伪装方法可阻止服务器使用已用过的 RAT重随机化混淆电路,但不包括那些与电路输入电线和电路输出电线相关的RAT.举例来说,设门电路i的RAT分别是(不采用数学伪装方法,因此,此时RAT是一个矩阵,而不再是 3个矩阵的乘法链),在每次外包计算中,客户端构造和并发送给服务器,其中,R0是单位矩阵,R1是随机置换矩阵(注意,这里仅使用 Kilian的随机化技术).此时,服务器就可计算,其中,表示已用于之前外包计算矩阵.另一方面,此时客户端开销与电路的大小具有相同的阶,这样,客户端可仅发送一个新的电路给服务器,实现上这样更容易.

同样地,利用 Kilian的随机化技术随机隐藏 RAT的每个部分,限制敌手以基本元素的方式操纵密文组件,比如不按序计算矩阵乘积.敌手有两类可能的攻击Kilian的随机化技术方法[25].

· 一类攻击方法是混合输入攻击,敌手正确计算矩阵链乘,但是不遵循矩阵链乘的结构.简而言之,和都前乘和后乘相同的矩阵,服务器可用代替计算矩阵链乘Zi,1,或者用代替计算矩阵链乘Zi,2.但是,给定电路输入电线的重随机化标签,服务器在逐个门电路检查重随机化电路时,并不能得到电路输出电线的正确重随化标签[13].

· 另一类攻击方法是部分计算攻击,敌手计算客户端不同输入下的部分矩阵链乘,试图通过比较这些中间值了解RAT的一些信息.例如,服务器在2个不同客户端输入下分别计算矩阵链乘Zi,1的前两个矩阵乘积,也就是,如果上述Kilian矩阵编码方案是理想的,则使用部分计算攻击的敌手并不能获得任何有用信息.

定理1.若DDH假设是存在的,则上述非交互可验证计算协议对外包函数f是安全的.

证明:接下来,采用模拟证明技术(simulation proof technique)[13,26]证明定理1成立.首先,先给出引理1和引理2及其证明.

引理 1.如果函数f是多项式时间可计算函数,由Garble(1,C)生成混淆电路的分布和由模拟器执行GarbleSim(1,C)生成混淆电路的分布在DDH假设下是计算上不可区分的.

证明:引理1的证明过程类似于Lindell-Pinkas关于Yao协议的证明过程[13].

首先描述模拟器的构造.模拟器执行GarbleSim(1,C),生成一个伪造的混淆电路,过程如下所述:对于混淆电路的每个门电路g,设其输入电线分别是a和b,输出电线为c;为电线a分别选择活动标签(active label)La和不活动标签(inactive label)La′,如果标签被用于计算混淆电路则称它是活动标签,同一电线的另一标签就是不活动标签.同样地,为电线b分别选择活动标签和不活动标签Lb,La′,为电线c选择活动标签和不活动标签Lc,Lc′.为该门电路随机选择 4个新 2ℓ-bit掩码δ1,δ2,δ3,δ4,计算并随机排序如下 4个密文对:

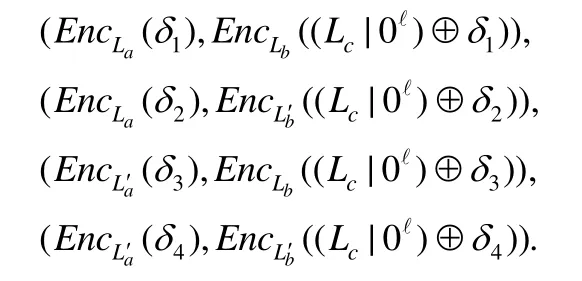
其中,所有密文对只加密输出电线的活动标签.上述所有的门电路构成了GarbleSim(1,C)生成的混淆电路.

为了证明模拟器产生混淆电路的分布与实际执行Garble(1,C)生成混淆电路的分布是计算上不可区分的,接下来使用标准的混合体论证(hybrid argument)[26],需定义一系列的混合体H0,H1,...,H|Γ|.

·H0:此混合体实际执行Garble(1,C)生成混淆电路Γ.

·Hi,其中,i∈(0,|Γ|):此混合体与H0的区别在于前i个门电路g1,...,gi的 4个密文对是由门电路输入标签所有4个组合加密门电路输出电线活动标签的密文组成,其他门电路与H0的混淆电路门电路相同.

·H|Γ|:此混合体执行GarbleSim(1,C)生成混淆电路,每个门电路都只有输出电线的活动标签加密.

对于所有i∈[1,|Γ|],任意两个连续的混合体Hi-1和Hi的区别在于:Hi-1中门电路gi输出电线不活动标签的密文在Hi中被输出电线活动标签的密文所取代.

假设门电路gi的输入电线分别是a和b,输出电线为c.电线分别是a活动标签和不活标签分别是,相类似电线b的分别是电线c的分别是中该门电路的4个密文对如下:

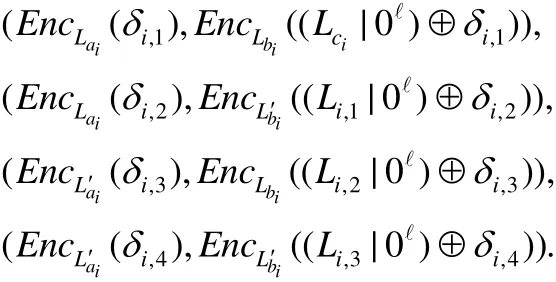
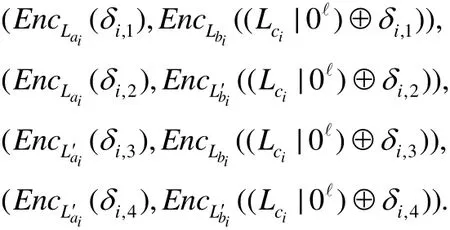
Hi-1和Hi是计算上不可区分的,这可通过归约到BHHO加密算法的语义安全得出.

假设存在PPT区分器D和多项式p(·),对无限多的n有:

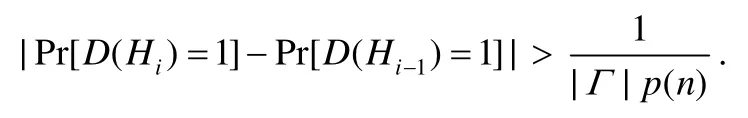
利用区分器D构造PPT敌手A,A接收门电路gi密文对并构造混淆电路,该电路一部分是Garble(1,C)真实产生的门电路,另一部分是GarbleSim(1,C)伪造产生的门电路.若A接收的门电路gi密文对与Hi-1中的门电路gi密文对相同,则该构造与Hi-1的混淆电路一致;若A接收的门电路gi密文对与Hi中的门电路gi密文对相同,则该构造与Hi的混淆电路一致.如果敌手A能够区分Hi-1和Hi,就可以区分其中门电路gi的密文对,这与 BHHO加密算法的安全性相矛盾. □

引理2.有效算法reRandGb输入为随机数r和Garble′(1,C)生成的混淆电路Γ′,输出电路C的重随机化混淆电路,则Garble(1,C)生成混淆电路Γ的分布和重随机化混淆电路的分布在DDH假设下是计算上不可区分的.

证明:引理 2的证明方法与引理 1的类似.为了证明以上两个分布是不可区分的,定义一系列的混合体H0,H1,...,H|T|,这里的T表示混淆电路的电线数量.

·H0.此混合体执行Gb.Garble(1,C)生成混淆电路Γ,使其输出与执行Gb.Garble′(1,C)生成的混淆电路Γ′输出相同,则混淆电路Γ的分布与混淆电路Γ′的分布是一致的.

·Hi,其中,i∈(0,|T|).此混合体生成的混淆电路前i根电线是由重随机化混淆电路Γ′的前i根电线得到,其他电线与混淆电路Γ′的电线相同.

·H|T|.此混合体是执行reRandGb生成的重随机化混淆电路,每根电线都是重随机化混淆电路Γ′的相应电线而得到的.

对于所有i∈[1,|T|],任意两个连续的混合体Hi-1和Hi的区别在于第i根电线在Hi-1中与混淆电路Γ′的第i根电线相同,而Hi的第i根电线是由重随机混淆电路Γ′的第i根电线而得到的.Hi-1和Hi是计算上不可区分的,这可由BHHO加密算法安全性得出. □

接下来,利用引理1和引理2证明定理1在两方计算下是成立的,那么定理1在可验证计算下也是成立的(我们考虑的不仅是可验证计算,还有在两方计算下的私有函数计算,见第5节).基于模拟的安全强于基于不可区分的安全,如果采用模拟证明技术证明协议是基于模拟的安全,则一定是计算不可区分安全(见定义2).因此,在证明中需构造恶意的服务器和恶意的客户端,并且模拟服务器的视图(view)与客户端的视图.定义一个模拟器Sim={Simc,Sims},Simc模拟客户端的视图,Sims模拟服务器的视图.

·Simc.给定客户端的输入x和计算结果y=f(x),构造模拟客户端的Simc.首先,一致随机选择矩阵;接下来计算矩阵乘积,为了生成混淆电路Γ,执行;然后选择客户端输入x相对应的输入电线活动标签;对输入电线i∈[n],执行reRandGb.InLabelSim(γi,ci)→γi(ci),其中,或.Simc剩下的步骤与客户端执行过程相同.

·Sims.给定客户端输入x和计算结果y=f(x),Sims模拟服务器构造混淆电路,其计算结果等于f(x).具体来说,执行,在中活动标签与相关联.考虑输入电线是a,b和输出电线为c的门电路,可用如等式(1)的4个密文对表示.然而,此时4个密文对只包含门电路输出电线的活动标签密文.Sims剩下的步骤与服务器执行过程相同.

为了证明协议执行过程的模拟器视图与协议实际执行是计算上不可区分的,需定义一系列的混合体,它们开始于客户端与服务器协议的真实执行,结束于充当客户端与服务器角色的模拟器理想执行.

·H0.此混合体中的客户端和服务器都遵循协议的实际执行(见第4.1节).

·H1.此混合体与H0的区别仅在于的计算方法.模拟器在计算中不采用Kilian的随机化技术,而是为客户端和服务器端都选择随机矩阵.

·H2.此混合体与H1的区别仅在于Zi,1,Zi,2的计算方法.Simc在计算中不采用数学伪装方法,而是直接计算.再者,Sims将Zi,1,Zi,2作为输入,执行,生成重随机化混淆电路.

·H3.此混合体与H2的区别仅在于由模拟器新构建混淆电路取代重随机化的混淆电路.具体来说,模拟器模拟客户端执行Gb.Garble(1,C),生成混淆电路;接下来为客户端输入x选取电路输入电线标签,执行Gb.Enc(gsk,x),生成输入的编码.相类似地,模拟器模拟服务器执行Gb.Garble(1,C),生成混淆电路.

·H4.此混合体与H3的区别仅在于由模拟器执行Gb.GarbleSim(1,C),新构建混淆电路取代原有电路.具体来说,模拟器模拟客户端执行Gb.GarbleSim(1,C),生成混淆电路;接下来为客户端输入x选取电路输入电线标签,执行reRandGb.InLabelSim(γi,ci),重随机化输入.相类似地,模拟器模拟服务器执行Gb.GarbleSim(1,C),生成混淆电路.

下面证明每个混合体与相邻的混合体是不可区分的.

引理3.对所有的概率多项式时间敌手.

证明:根据 Kilian的随机化技术正确性,返回给敌手A的矩阵分布上并没有变化.因此,敌手A赢得H1的概率仍然与赢得H0的概率相同. □

引理4.对所有的概率多项式时间敌手.

证明:敌手A赢得H1的概率与赢得H2的概率相同,因为否则就存在一个攻击者对数学伪装方法具有不可忽略的优势. □

引理5.对所有的概率多项式时间敌手.

证明:根据引理2的证明可以得出:给定一个由Gb.Garble(1,C)生成的混淆电路以及由reRandGb生成的重随机化混淆电路,没有计算能力受限的敌手能够区分这两个电路.这意味敌手A在H3中的概率与在H2中的概率相同. □

引理6.对所有的概率多项式时间敌手.

证明:根据引理 1的证明可得出:由Gb.GarbleSim(1,C)得到的电路与由Gb.Garble(1,C)得到的电路,没有计算能力受限的敌手能够区分这两个电路.这意味敌手A在H4中的概率与在H3中的概率相同. □

接下来说明在基于模拟的安全下客户端不会接受敌手A伪造的计算结果.若敌手A不能使验证算法接受一个不正确的输出,则可验证计算方案是安全的(见定义2关于可验证计算方案是计算不可区分安全的定义).为了说明客户端不会接受敌手A伪造的计算结果,需要给定输入x和计算结果y=f(x),构造客户端模拟器具体过程如下.

3.敌手A向预言机PVerify发起查询,预言机返回acc,当且仅当Verify(sk,σx,τx)→(acc,y).预言机 Pverify仅返回接收/拒绝比特acc.

4.步骤2和步骤3可重复多项式次数.

5.给定敌手A的σy,Sim′c生成(acc,y)←Verify(sk,σy,τx).如果σy是伪造的计算结果,Simc′将不能映射出正确的混淆电路输出标签,则acc=0(拒绝),输出⊥;否则,acc=1(接收),并输出y.

综上所述,定理1得证. □

定理2.若DDH假设是存在的,则上述非交互可验证计算协议对服务器是隐私的.

证明:该证明与定理1的证明都具有类似形式的混合体和证明过程.服务器的隐私性可由RAT的隐私、可重随机化的混淆电路安全性和Yao的混淆电路安全性得出. □

4.3 适应性安全

静态安全的混淆电路是指输入不依赖于混淆电路[13,27](见定义7).与之相反,适应性安全的混淆电路是指,如果敌手在查看混淆电路以后还允许适应性地选择输入,此时混淆电路仍是安全的(见定义8).Yao的混淆电路只能做到静态安全的,这是因为为了提高在线阶段的效率,混淆电路的生成和发送通常都在离线阶段,恶意的敌手就有可能根据混淆电路自己选择输入,使得混淆电路不再安全.文献[3]的可验证计算方案使用了 Yao的混淆电路,为了保证方案的安全,必须在发送混淆电路之前确定输入,因此该方案是静态安全的.

第4.1节的可验证计算协议虽然也是静态安全的,但可采用两种方法实现适应性安全:一种方法是将该协议运用复杂性杠杆(complexity leveraging)实现适应性安全;另一种方法是将该协议作细微的调整,即可做到适应性安全.为了使恶意的敌手在离线阶段不能根据混淆电路自己选择输入,客户端只需将所有门电路的密文对的前半部分和后半部分别与一个大小合适的随机可逆矩阵相乘.相应的,构造矩阵修改为,计算,再将现在的Zi,1,Zi,2用于随机化门电路i.上述过程既没有将 RAT泄露给敌手,也保证敌手不能尝试混淆电路的输入,即实现了适应性安全.为了说明这一点,可采用文献[27]中静态安全转换为适应性安全的构造方法.具体来说,因为定理1成立,故存在静态安全 PPT模拟器S,对任意PPT敌手A(见定义7),

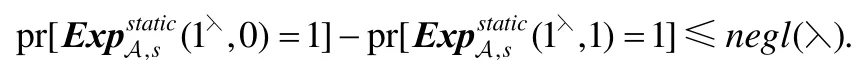
给定任意适应性安全PPT敌手A1,构建静态安全敌手A.若由模拟器S能够构建适应性安全PPT模拟器S1:

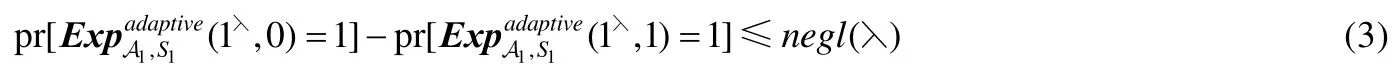
则适应性安全成立(见定义8).

1.挑战者随机选择比特b1.

2.敌手A1向挑战者提交C,挑战者返回..如果b1=0,挑战者返回随机混淆电路;如果b1=1,挑战者也返回随机混淆电路.

3.敌手A1向挑战者提交x.

4.如果b1=0,则挑战者调用定义7的步骤3,生成,并将所有门电路的密文对的前半部分和后半部分别与相乘生成,并返回和.

5.如果b1=1,则挑战者调用定义7的步骤4,生成和,并将所有门电路的密文对的前半部分和后半部分别与相乘生成,并返回和.

6.最后,敌手A1输出猜测比特,如果,敌手A1获胜.

设b是定义7的挑战比特,从上述适应性安全实验可以得出:

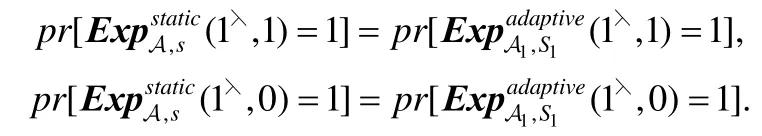
所以,等式(3)成立.

5 可重用的密码转置防火墙

接下来,将第 4.1节的协议应用于密码转置防火墙[23],从而提供一种密码转置防火墙的新模式,即可重用的密码转置防火墙.密码转置防火墙聚焦于用户与外部通讯的密码安全,可解释为一个状态算法,应用于用户发送和接收已由某些密码算法处理的消息.两方计算下的私有函数计算PFE协议有一对参与方分别是Alic和Bob,Alice拥有私有的函数f,Bob拥有私有的输入x,双方计算f(x)并保证输入x和函数f的隐私性和结果的正确性.PFE协议的密码转置防火墙主要技术工具是可重随机化的不经意传输和可重随机化的混淆电路.Bob(Bob的密码转置防火墙)和Alice(Alice的密码转置防火墙)执行可重随机化的不经意传输,Alice向Bob透露电路输入电线的两个重随机化标签其中之一,而不了解确切是哪一个.接下来,Alice的密码转置防火墙将重随机化的混淆电路发送给Bob,Bob就可以根据重随机化标签计算电路.然而,Alice的密码转置防火墙重用用于重随机化电路的Yao的混淆电路是不安全的,这是因为重复的重随机化等同于混淆电路的重用.所以,我们提出一种可重用的密码转置防火墙,用户一次生成混淆电路,接下来,密码转置防火墙可安全地重随机化多次.

5.1 不经意传输

Naor-Pinks/Aiello-Ishai-Reingold证明了不经意传输协议可在诚实但好奇模式下是安全的[28,29].不经意传输协议有两个参与方:发送方Alice和接收方Bob.Alice的输入为a0,a1∈{0,1};Bob的输入是选择的比特b∈{0,1}.Alice和Bob之间协议实现如图3所示,其中,G是阶为q的群.

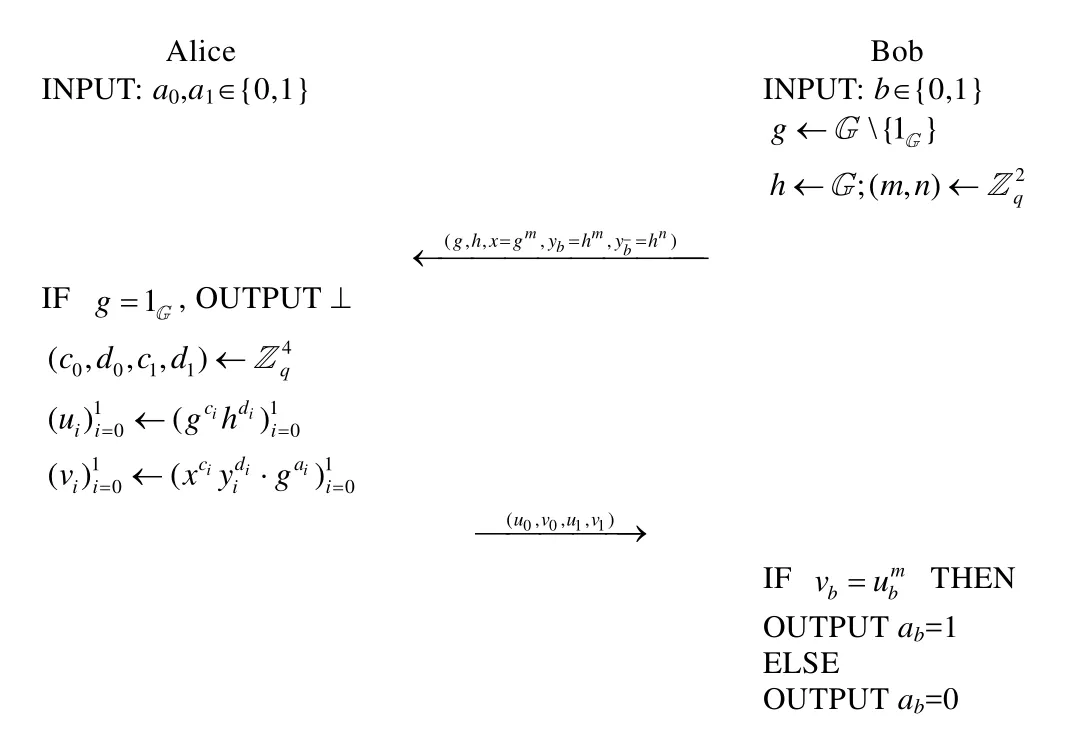
Fig.3 Oblivious transfer(OT)protocol图3 不经意传输协议OT

定义10(可重随机化的不经意传输).如图3所示两消息的不经意传输协议,设msg1=(g,h,x,y0,y1)是第1轮的消息,msg2=(u0,v0,u1,v1)是第2轮的消息.

不经意传输协议是可重随机化的,若存在输入为msg1,msg2和随机数r的有效算法reRandOT,即使给定r,b,a0,a1,msg1,msg2,以下两个分布是计算上不可区分的.

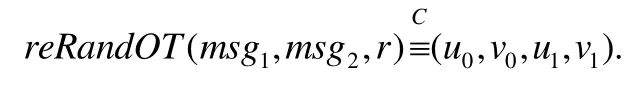
5.2 私有函数计算的可重用密码转置防火墙

Alice的PFE可重用密码转置防火墙WA的构造与可验证计算协议的构造非常类似,技术上的区别在于,WA需要定义如何构造不经意传输的重随机化.因为Bob的可重用密码转置防火墙WB与文献[23]的不经意传输协议重随机化是一致的,故此处省略.构造Alice的PFE可重用转置密码防火墙如图4所示.本质上该构造与可验证计算协议相同,安全要求相同,证明也类似.

定理3.若DDH假设成立,如图4所示的Alice的可重用密码转置防火墙对于函数f是正确的和安全的.

证明:Alice的可重用密码转置防火墙的正确性证明如下.

G是素数阶q的循环群,定义是Bob发送给Alice的初始消息,Bob的防火墙安全性可直接由DDH假设得出.恶意模式下的可重随机化不经意传输安全和可重随机化混淆电路安全确保Alice的防火墙是安全的.接下来证明可重随机化不经意传输的安全性.

Fig.4 Alice’s reusable cryptographic rerverse firewall for the private function evaluation protocol图4 私有函数计算协议中Alice的可重用密码转置防火墙

WB·(WA·Alice)对来自 Bob的任意有效消息(g,h,x,y0,y1)以不可忽略的概率做出一致随机有效响应.若,则是一致随机群元素.为了说明这一点,需要利用等式(或者).若(或),的分布是一致和独立的.

1.输入比特σ,SimA产生.

2.随机选择(a0,a1)←{0,1}和.

SimA的输出与在真实协议中Bob接收来自 Alice的可重用密码防火墙的消息是不可区分的,这可从 DDH假设得出. □