典型去噪算法在圆形线材表面缺陷图像中的对比研究

杨培义，张天彤，杨辰飞，王若飞

（郑州铁路职业技术学院，郑州450046）

0 引言

东莞市某钢铁线材公司的主要产品是高精度线材，由于各种原因使得其表面产生多种缺陷，导致合格率不高[1]。现在的圆形线材表面缺陷检测装置前期需要进行表面缺陷图像采集，并转换为数字图像。数字图像是人类获取信息的重要来源，在数字图像生成、传输、压缩、储存、变换等过程中，由于受到一些不可避免的外界或内部环境的影响，图像难免会受到污染，产生图像噪声[2]。其中外界环境主要包括光照、温湿度、图像设备、机械设备反复振动等，内部影响主要包括电阻、电流、电子设备元器件、传感器等。图像噪声的产生使得图像退化失真，图像的特征与细节模糊，严重干扰视觉效果，给后期的处理分析带来较大麻烦[3]。因此，为了解决该难题，很多学者进行了许多图像去噪的算法对比分析。如刘丽梅[4]等人对中值滤波技术的发展研究进行了总结；付炜[5]等人提出一种改进的小波域阈值去噪算法；郭晓霞[6]等人提出一种小波去噪中软硬阈值的一种改良折衷法，该法相比软、硬阈值法更加灵活、优越；兰超[7]等人研究了一种基于改进的软硬阈值折衷法的去噪算法；万小红[8]进行了常用图像去噪方法探析与比较的研究，得出单种去噪算法均具有一定的局限性；中国电子科技集团公司的董文德[9]等人经过分析建模，提出一种泊松噪声污染模糊图像的非盲去卷积方法。经分析对比，上述方法具有一定程度的图像去噪效果，但效果仍不够理想。现结合圆形线材厂区设备、环境等因素与MATLAB 软件，对采集的圆形线材表面缺陷（以脱皮缺陷为例）的数字图像分别添加三种经典噪声：高斯噪声、椒盐噪声和泊松噪声，然后分别进行均值滤波、中值滤波、高斯滤波，并进行了对比分析，这里采集的图像已经过数字灰度化[10]。

1 图像噪声

1.1 高斯噪声

在过往学者的研究图像噪声的基础上得出，高斯噪声，即正态噪声，符合正态分布，是一种随机噪声，在自然界中最常见，很多设备及电子元器件都属于高斯噪声。通常用空域滤波的平滑操作或图像复原技术来消除高斯噪声[11]。

设高斯噪声中随机变量为z，其对应的概率密度函数为Ρ(z) ，则：

明显地，高斯噪声随机变量z 服从正态分布，正态分布是具有两个参数u 和σ2的连续型随机变量的分布，u 是遵从正态分布的均值，σ2是z 的方差，正态分布记作

1.2 椒盐噪声

椒盐噪声是一种黑白相间的亮暗点噪声，产生于传输或处理等过程中，由信号脉冲强度引起，是以称为脉冲噪声。椒盐噪声包括盐噪声（Salt Noise），胡椒噪声（Pepper Noise）。盐是白色，椒就是黑色。盐噪声属于高灰度，胡椒噪声是低灰度。通常图像上显示的黑白杂点，表示二者同时出现[12]。

椒盐噪声的概率密度函数为：

椒盐噪声，即是图像中出现的噪点只有两种灰度值，用a 和b 表示，对应的概率用Pa、Pb表示。此噪声的均值和方差分别为：

椒盐噪声主要表现为短暂地在成像中停留，常用中值滤波法去除脉冲干扰和椒盐噪声。

1.3 泊松噪声

泊松噪声，即噪声服从泊松分布模型。泊松分布是概率论中几大常见的分布函数之一，属于离散型随机变量的分布[13]。

假设为X 泊松噪声中的随机变量，其相应的概率分布函数为：

称X 遵从的泊松分布，参数为λ，X～P（λ）。式中λ为噪声中泊松流强度，并且为大于零的常数。其中对泊松分布有：E（X）=D（X）=λ，即符合泊松分布的噪声的期望值和方差都等于参数λ。

2 图像噪声添加实验结果

以脱皮缺陷原图为代表进行噪声添加，其中高斯噪声均值为0，方差为0.02；椒盐噪声密度取值0.02；泊松噪声使用缺省参数。

图1 脱皮原始图像

图2 添加高斯噪声

图3 添加椒盐噪声

图4 添加泊松噪声

3 图像去噪算法

在保证图像清晰度的前提下，好的图像噪声抑制算法至少要达到以下三点要求：①有效去除均匀区域噪声；②较为完整地保留图像边缘与纹理特征；③不产生伪吉布斯效应。针对上述三种常见噪声，拟用中值滤波法、均值滤波法、高斯滤波法三种算法，对噪声图像降噪。

3.1 均值滤波法

下面展示两种邻域点集合模板：4 邻域点和8 邻域点。

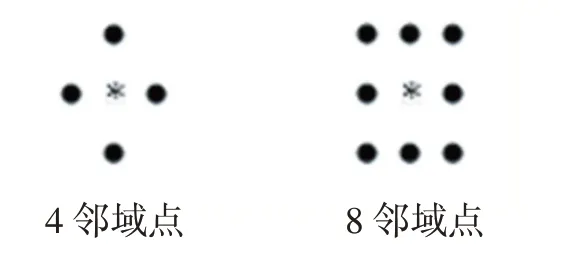
图5

所选邻域半径的大小决定了滤波后的对应效果。邻域半径越大，处理后的图像边缘显得越模糊。

3.2 中值滤波法

中值滤波法是一种典型的非线性空域滤波法，同时也是比较常用的图像平滑技术，一直以来被广泛应用于语音处理、图像增强与恢复等领域中。

中值滤波是以排序统计理论为基础的非线性信号处理技术，能够有效减弱或消除噪声。它用每一像素点某邻域窗口内的所有像素点灰度值的中值（若邻域窗口中有偶数个像素，则取两个中间值的平均值）取代该点的灰度值。因为噪声相比周围的像素反差较大，所以含有噪声的像素点非暗即亮。假如在某一邻域内将像素点依据灰度值大小排序，噪声点一定处于序列两端，然后输出中间灰度值，进而消除孤立噪声点[15]。其中中值滤波法利用两种不同尺度模板，分别为3×3和5×5。

3.3 高斯滤波法

高斯滤波也属于线性滤波，其对应的滤波器需要依据高斯函数的形状来选择权值，主用于减弱或消除高斯噪声，十分有效，普遍被用于数字图像后期应用中的去噪环节。简单来说，高斯滤波过程便是对整个图像加权平均，基本思想大体上同邻域平均法，但不同的是每个像素点的值，是由包括该像素点在内的邻域内像素值通过加权平均后获得[16]。

高斯滤波的具体操作是：用一个掩模扫描图像中的所有像素，将掩模确定的邻域内像素的灰度值进行加权平均，然后取代掩模中心像素点的值。

常用的掩模包括3×3 或5×5 两种，对应的权值分布如图6 所示。

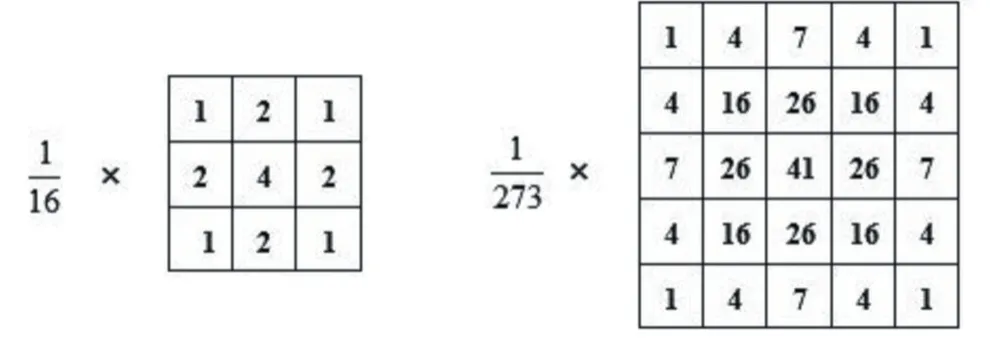
图6

4 图像去噪实验效果分析

针对上述三种噪声类型，分别用三种滤波算法进行去噪处理。首先是针对均值为0，方差为0.02 的高斯噪声分别用三种滤波算法进行降噪，效果如图7-图9 所示。

图7 高斯噪声均值滤波法降噪效果

图8 高斯噪声中值滤波法降噪效果

图9 高斯噪声高斯滤波法降噪效果

其次对密度值为0.02 的椒盐噪声分别用三种滤波算法进行降噪，效果如图10-图12 所示。

图10 椒盐噪声均值滤波法降噪效果

图11 椒盐噪声中值滤波降噪效果

图12 椒盐噪声高斯滤波法降噪效果

最后对使用缺省参数的泊松噪声分别用三种滤波算法进行降噪，效果如图13-图15 所示。

图13 泊松噪声均值滤波法降噪效果

图14 泊松噪声中值滤波法降噪效果

图15 泊松噪声高斯滤波法降噪效果

由图7-图15 可知：无论对于何种噪声类型进行滤波，8 邻域均值滤波法滤波效果优于4 邻域模板滤波，但同时考虑计算中间的复杂性，模板的选择有待于考察；相比高斯噪声和泊松噪声，中值滤波法更适用于带有椒盐噪声的图像，滤波效果更好，同时保留了边缘信息；高斯滤波器在5×5 掩模下对高斯噪声图像处理效果比3×3 掩模下的处理效果好，对高斯噪声图像的处理比对椒盐噪声图像及泊松噪声图像处理的效果更好。

5 去噪算法效果分析

经上述脱皮缺陷图像去噪效果分析，依据上述提到的图像噪声抑制好的算法的三点要求得出：

（1）针对不同噪声类型的数字图像，应采用不同的降噪算法进行滤波；

（2）对于高斯噪声，同等条件下，高斯滤波法效果最佳，中值滤波法次之，8 邻域模板均值滤波算法处理效果最差；

（3）对于椒盐噪声，同等条件下，中值滤波法处理效果最理想，其次是8 邻域均值滤波法，高斯滤波法效果排最后；

（4）对于泊松噪声，同等条件下，8 邻域模板均值滤波法与中值滤波法都比较适用，效果相对理想。

6 结语

均值滤波法速度快，算法简单，但无法消除噪声，只能减弱，但降噪的同时会产生模糊，尤其在边缘和细节处，半径愈大，图像愈模糊；中值滤波法能够较好地去除图像中椒盐噪声，同时保护图像边缘细节信息，去噪效果明显优于均值滤波法，但不适用于某些细节多，尤其对于线、尖顶等细节多的图像；高斯滤波法对高斯噪声图像处理效果明显最佳，优于均值滤波法和中值滤波法。因此，可以将多种算法结合或者改进来完成对多种图像噪声进行滤波。