机器博弈中搜索策略和估值函数的设计

何轩 洪迎伟 王开译 彭耶萍

摘要：机器博弈是人工智能的头部领域。该文以六子棋为例，重点介绍了搜索策略和估值函数的设计，主要介绍了博弈树，极大极小值算法，α-β剪枝，MCTS以及基于“路”和“棋型”结合的估值函数。

关键词：六子棋;搜索算法;估值函数

中图分类号：TP391 文献标识码：A

文章编号：1009-3044（2019）34-0053-02

1 概述

作为二十一世纪三大尖端技术之一的人工智能，其头部研究领域的机器博弈被认为是最富有挑战性的项目之一。而由吴毅成教授所提出的六子棋，以其玩法简单，情况多变，丰富的乐趣性吸引了大量玩家，并且成为机器博弈的竞赛项目之一。

2 搜索算法

2.1 博弈树搜索

搜索的目的不仅是找出当前所有可以落子的地方，还要考虑到之后更多步数所产生的情况。博弈树指的是以树的形式把对手和计算机所有落子的情况表示出来。

该博弈树以当前局面为根节点，每一个节点表示一个推导的局面，每一层表示一方所有可能的落子情况，树的层数表示搜索深度。该树描述的是以当前局面为起始，走n步以后的所有情况。

单纯的博弈树效率很低，所以真正的棋手那样，过滤掉许多不需要考虑的情况，降低搜索的深度，通过改进算法实现在规定时间求出最佳路径。

2.2 极大极小值搜索

假设双方都采用最佳的策略，每一种局面都通过估值函数来确定局面的好坏，那么对于己方来说每次都要选择最好的，每次都认为对方选择的是最佳策略，选择估值最低的局面展开博弈树。

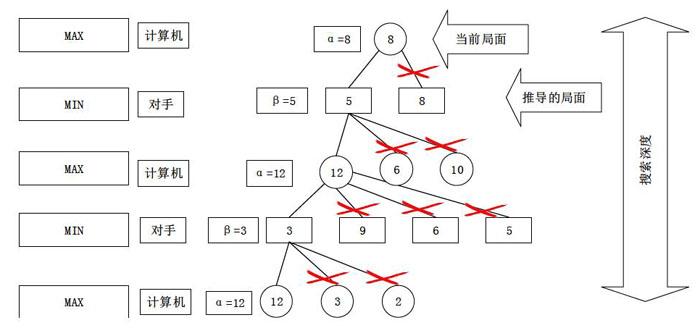
2.3 α-β剪枝

α—β剪枝是在极大极小值搜索的基础上，舍弃每一次局面没有必要继续搜索下去的情况。对于MAX的情况来说，只保留最大的分支，对于MIN的情况，只保留最小的分支。

2.4 MCTS树搜索

如果直接把α-β剪枝算法直接应用于实际的机器博弈，会有几个问题。

1）即使剪枝过后，推导的局面还是太多。

2）对于每一个局面，如果为了得出每一层准确的估值，而进行相同时间的搜索，会导致搜索的深度不够，无法建立更加深层次的博弈树。

舍弃绝对不合理的局面后，人类棋手一般会选择一个看起来特别有价值的局面做深入推演，而并不是同时推演几个待选局面。

蒙特卡罗树分为四个部分，图中每一个结点代表一种推导出来的局面，左边是总胜利次数，右边是总模拟次数。

1）选择

从根节点开始依次遍历孩子节点中胜率最高的，直到叶子节点。

2）扩展

给该叶子节点添加一个新的孩子节点。

3）模拟

新的孩子节点进行胜率模拟。

4）回溯

把模拟结果从孩子节点开始一直回溯到根节点本身。

蒙特卡罗树能够快速深入推演比较有价值的局面，舍弃获胜概率比较小的节点，不推演其子节点，使得搜索深度大大增加，但是也有可能一开始就误人歧途，因为可能推演到最后发现推演的这个分支的胜率没有其他分支的高。

3 估值函数

3.1 基于“路”和“棋型”結合的估值函数设计

现在大部分的棋博弈中，都是基于棋形结构的分析，这种结构有一种高度模型匹配的算法在里面，所以这就对于准确定位棋形的模型的要求很高。不仅模型构建对空间的占用率大，而且后期计算机对棋形的匹配费时较大，这样使得算法的时间和空间复杂度都很高。因此对棋形的预判效率是衡量“棋型”估值函数算法好坏的关键。六子棋常见棋形有19种，常用的位置信息有眠五、眠四、活五、活四，每一种棋形又存在多种交叉情况如图1、图2，这就更加使得对棋形的预判难度加大，所以如何有效和精准地预判，搜索棋形，已经成为六子棋机器博弈的难题。

下面，我们分析一下“路”这种思想是如何在棋盘中进行模拟的？我们现实当中的路，有弯曲的、有笔直的，但是在棋盘当中，“路”的思想，其实就是数学理论中的一个结论，即若知道两个点，那么在两点之间必定可以确定一条直线。所以在棋盘中的“路”，就是指在棋盘上存在两颗棋子，在这两颗棋子之间，还经过了4枚同色的棋子。由于每条“路”都是连续的6个点位，如果把每一个位点换成0和1的二进制码，白棋是10，黑棋是01，空格是00，然后用计算机的空间数组存储每一条路的串码，那么对于计算机的预判和运算是不是得到了很大的优化。例如，某“路”中已经存在4颗子，就不用再去判断它到底是活四、眠四、跳四等棋形。同时，如果把“路”定义为一种类，“路”的一些特点是类的属性，那么我们就可以利用面向对象的思想，对“路”的估值函数进行优化。这样能方便地予以实现“路”的特点，以便于预判。

“路”的总数较少。现在我们以六子棋为例，按照横向、纵向、左斜、右斜4个方向的特点，可以分别计算出六子棋在各个方向的“路”的数目和情况：

1）横向，19行x （19 - 6+1）路/行=266路，如图3的三种情况;

2）纵向，19列x（19- 6+1）路/列=266路;如图4的四种情况;

3）左斜，14行x （19 - 6+1）路/行=196路;如图5的四种情况;

4）右斜，14列x （19- 6+1）路/列=196路;如图6的四种情况。

因此，在19x19围棋盘上，总共有266x2+ 196x2= 924（路）。如果我们采用“路”来预判棋形状态值，那么对于六子棋的估值评估函数设计则是一种优化，它不再需要消耗大量的时间对棋形进行匹配。

到了这里，我们又要回到之前对“棋形”模型匹配的估值函数算法的问题和不足，前面讲的“路”值估值方法，可以说是对棋局评估函数的一种建立和优化。

参考文献：

[1]李学俊.六子棋中基于局部“路”扫描方式的博弈树生成算法[J].智能系统学报，2015，10（2）：267-272.

[2]周新林.六子棋博弈系统设计与实现[J].软件导刊，2015，14（3）：92-94.

[3]闵文杰.六子棋计算机博弈关键技术研究[D].重庆：重庆交通大学，2010：88.

[4]陈光年.基于智能算法的六子棋博弈行为选择的应用研究[D].重庆：重庆理工大学2010：76.

[5]王小龙.连珠模式棋类博弈的搜索优化[D].合肥：安徽大学，2014：74.

[6]张小川.六子棋博弈的评估函数[J].重庆：重庆理工大学学报：自然科学版，2010，24（2）：64-68.

【通联编辑：朱宝贵】

收稿日期：2019-10-15

作者简介：何轩（1999-），男，吉首大学软件工程专业本科在读;洪迎伟（2001-），男，吉首大学软件工程专业本科在读;王开译（1999—），男，吉首大学软件工程专业本科在读;彭耶萍（1981-），女，主要研究方向为数据挖掘及算法。