时滞多智能体网络中的Push-Sum分布式对偶平均算法研究

周小清

(重庆师范大学数学科学学院， 重庆 401331)

在基于局部信息交互的资源配置和传感器网络之间的信息交换中都涉及复杂多个体系统。复杂的多个体系统中，每个个体有一个目标函数，整个网络系统的目标函数可表示成每个个体的目标函数之和。解决这类优化问题主要有3类算法，即原始算法[1]、对偶算法[2]和原始对偶算法[3]。解决实际问题时，个体的信息交流会出现滞后的现象。信息从个体出发后，需要经过相对较长的时间才能到达接受的个体，就是所消耗的时间比正常时间长，这样的信息延迟被称为状态的延迟[4,5]。此外，还有一种信息延迟现象，被称为梯度信息延迟[6]，即每个个体接收的梯度信息不是当前的梯度信息，而是延迟后的梯度信息。网络系统的信息交流出现信息延迟现象，会对网络结构造成一定的影响。本次研究，主要针对梯度信息延迟现象，讨论多智能体网络中的分布式凸优化问题。

文献[7]研究有向通讯网络中时间不变的分布式优化问题，提出了Push-Sum对偶平均次梯度算法，对应的通讯矩阵是列随机的，但没有考虑次梯度出现时延的情况。文献[8]研究时变有向网络下的分布式优化问题，给出了次梯度推进算法的收敛性分析，但仅考虑了无约束优化的情况。文献[6]研究时间不变的无向通讯网络的分布式优化问题，考虑了次梯度信息会出现延迟的情况，但没有涉及Push-Sum协议，并且要求通讯矩阵是双随机的。对通讯矩阵的双随机要求，意味着个体进行信息通讯时的网络必须是平衡的。受到这些文献的启发，笔者提出了一种Push-Sum分布式对偶平均优化算法。该算法引入了Push-Sum协议，对应的通讯矩阵是列随机的，而不必是双随机的；在信息传递的过程中，每个个体接收的是过时的梯度，而不是当前的梯度；尽管有时延的状态，运用时滞的Push-Sum对偶平均次梯度算法，仍然能使得目标函数渐近地达到最优。同时，分析了延迟对收敛速度的影响。

1 问题描述

(1)

式(1)中：X为约束集，X⊂Rd，为Rd维空间；fi(x)为凸函数，fi(x)：X→R，并且对于范数‖·‖是 Lipschitz连续，即 |fi(x)-fi(y)|≤L‖x-y‖,∀x,y∈X。对于任何x∈X和任何次梯度gi(x)≤∂fi(x)，有 ‖gi‖*≤L，其中‖·‖*为‖·‖对偶范数，定义为 ‖v‖*=sup‖u‖=1〈u,v〉。

2 提出的算法

(2)

(3)

(4)

(5)

其中，gi(t-τ)为次梯度，是fi(xi(t-τ))在x=xi(t-τ)的次梯度，τ是表示常数延迟的正整数。对于所有的i，初始化：wi(0)=1，zi(0)=0，gi(0)=0。投影算子定义为：

为了叙述方便，引入以下记号及相关定义和假设。

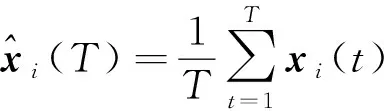
并且

由矩阵A的列随机性，可得：

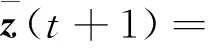
(6)

定义1[9]：给定一个紧的凸函数ψ(·):Rd→R，定义一个Bregman散度。相应的定义为：

Dψ(x,y)=ψ(x)-ψ(y)-〈▽ψ(y),x-y〉

假设1[3]：(1)图序列{G(t)}是B-强连通的；(2)每个函数fi是凸的，i>0。

首先，以下引理成立。

引理2[8]：令x+minmize〈z,x〉+Aψ(x)，对于∀x∈X，有：

〈z,x〉+Aψ(x)≥〈z,x+〉+Aψ(x+)+ADψ(x,x+)

引理3[8]：令图序列{G(t)}是一致强连通的。采用记号A(t:s)，即A(t:s)A(t)…A(s)，t≥s≥0。则

(a) 存在一个随机向量序列{φ(t)}，即φ(t)∈Rn，且t≥s,A(t:s)-φ(t)1′呈几何级数退化。对于所有的i和j(i=1，2，3，…，n；j=1，2，3，…，n)，有：

|[A(t:s)]ij-φi(t)|≤Cλt-s

其中，对∀i,j有t≥s≥0，C为常数，C>0，λ∈(0，1)。

3 主要结论

首先，针对个体之间造成的不平衡的现象，证明了各个个体之间有一个上界；然后，为了简化证明，将引理5和引理6作为时滞的Push-Sum对偶平均次梯度算法的2个独立性质，从证明中分离出来；最后，对时滞的Push-Sum对偶平均次梯度算法的收敛性进行了分析。

3.1 主要引理

为了得到时滞的Push-Sum对偶平均次梯度算法的收敛性，先证明一个重要引理。

引理4：考虑序列{zi(t)}。假设图序列{G(t)}是一致强连通，则对于所有t，t≥1，有：

其中，δ>0，λ∈(0，1)，满足δ≥1

【证明】 由式(2)，递推可得：

=…

(7)

由式(3)，递推可得：

由zi(0)=0，有：

(8)

(9)

因此，在t≥0时，结合式(7)(8)(9)，并且在式中加上一个φ(t-1)，再减去一个φ(t-1)，据引理3，可得：

由范数满足三角不等式，则有：

据引理3的δ的定义，且τ是一个正整数，λ∈(0，1)，即有：

引理5[6]：对于任意的x*，x*∈X，有

引理6[6]：对于任意的x*，x*∈X，有

【证明】 由引理6，可得

(10)

根据xi(t)的迭代式和范数的性质，且

则有

[a(t-s-1)-a(t-s)]ψ(x*)

(11)

将式(11)代入式(10)，并利用 (A+B+C+D)2≤4(A2+B2+C2+D2)，可以得出

(12)

结合引理4的结果和步长的非负单调递减性，经过计算，将式(12)化简可得：

3.2 算法的收敛性分析

【证明】 由f(x)的凸性，可得

(13)

首先，估计式(13)的前2项。因为gi(t)是fi在xi(t)的次梯度，gi(t)∈∂fi[xi(t)]，根据fi的凸性和Lipschitz连续性，有

(14)

根据ei(t)=gi(t)-gi(t-τ-1) 的定义，则有

〈gi(t),xi(t)-x*〉 =〈gi(t-τ-1),xi(t)-x*〉+〈ei(t),xi(t)-x*〉

=〈gi(t-τ-1),h(t)-x*〉+〈gi(t-τ-1),xi(t)-h(t)〉+

〈ei(t),xi(t)-x*〉

〈ei(t),xi(t)-x*〉

(15)

其次，估计式(13)的最后一项。根据fi的Lipschitz连续性，有

(16)

将式(14)(15)(16)代入式(13)，并结合引理4、引理5、引理6，则有

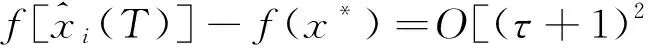
4 结 语

研究提出了时滞的Push-Sum分布式对偶平均算法。运用此算法，各个节点的变量最终会收敛到最优点的附近。时滞的Push-Sum分布式对偶平均算法，在信息接收过程中接收的是过时的梯度，而不是当前的梯度。通过建立时滞的梯度信息，证明尽管有时滞的状态，本次提出的算法仍然能使目标函数渐近地达到最优，它保持了网络拓扑的性能优势。针对延迟对收敛速度的影响问题，通过利用Bregman散度，说明了延迟在收敛中的作用，且速度是O[(τ+1)2由此可知，由延迟引起的优化误差是二阶的，当延迟固定时，随着T的增加，收敛速度逐渐趋于0。