基于广义斯涅尔定律的声超常反射
,
(南京航空航天大学 应用物理系, 南京 211106)
当前声学研究中,超材料的研究是一个热点问题。所谓的超材料是一种人工复合成的材料,通常由结构尺寸远远小于工作波长的单元周期性或非周期性排列组合而成[1-2]。声学超材料能产生很多自然材料无法产生的特殊物理现象,例如亚波长成像、自准直、超透射、反常多普勒效应[3]、声波的负折射[4-5]等。声学超材料的产生无疑给自由调制声波的设想提供了新思路。笔者正是基于超材料的研究,对传统的声反射理论进行了修正,从而实现了声波的异常反射。
根据传统的声学反射理论,当声波以某个特定角度入射平面时,反射声波也必定按照同等大小的反射角度出射。如果能够通过改变反射平面的结构来实现任意反射角的调制,那么在日常生活中会达到意想不到的效果。文章采用的广义Snell(斯涅尔)定律可以很好地满足上述要求,该理论通过在反射平面设置特殊的反射相位结构,使得声波打破原有的规则沿着特定的反射角度出射。根据这一理论,结合COMSOL仿真,设计了一种特殊的声学微结构来实现180°的相位差,从而控制正入射条件下的反射声波,且在此基础上利用3D打印技术对此声学微结构进行了试验,仿真和试验结果成功地验证了广义Snell定律。
1 方法论述
Snell定律最初是一条描述光的反射折射规律的定律,是指光从一种介质射向另一种介质时,在界面处会发生反射和折射现象,入射角与折射角的正弦值与入射角无关,而与介质的相对折射率有关[6]。其通常的表达式为
n1sinθ1=n2sinθ2
(1)
式中:n1和n2分别为两种介质的折射率;θ1和θ2分别为光的入射角和反射角。
由于声的传播与波的性质有关,因此该定律同样适用于声传播,其具体的表达式为
sinθr=sinθi
(2)
式中:θr为反射角;θi为入射角。
即声波在传输过程中遇到平面介质发生反射时,遵从反射角等于入射角的定律。
Snell定律作为波传播的基本理论一直被相关领域的学者所遵循,但是2011年Science上发表的论文对该理论进行了修正,这便是广义Snell定律[7]。其具体推导见参考文献[8-11]。
根据费马原理,光在两点之间总是按照光程取极值的方向传播。同时对于光波来说,光程的变化也代表着相位的变化,故光的传播也需沿着相位取极值的方向[12-14]。

图1 两条无限接近的光路示意
两条无限接近的光路示意如图1所示,假设光从A点出发经反射界面反射后到达C点。从中选取两条无限接近的光路ABC和ADC。光经过这两条光路时产生的相位变化应是相等的,即光在BE这段光程中产生的相位变化与在B点反射时产生的相位变化之和应该等于光在ED这段光程中产生的相位变化与在D点反射时产生的相位变化之和,则有
knsinθidx+φ+dφ=knsinθrdx+φ
(3)
式中:n为折射率;x为声传播距离;φ为相位;k为光在介质中的波矢。
整理则有
(4)
式中:λ为光波的波长;dφ/dx为x方向的相位梯度。
由于该定律的推导只利用了光的波动性,基于光声直接的类比特性,可将广义的Snell定律应用到声学领域,即
(5)
式中:dφ/dy为y方向的相位梯度。
若声波以垂直方向进行入射,广义Snell定律原理示意如图2所示,则反射角可表示为
(6)
由此便实现了声波正入射条件下反射角的偏转,只需改变入射声波频率,便可获得不同角度的反射角。
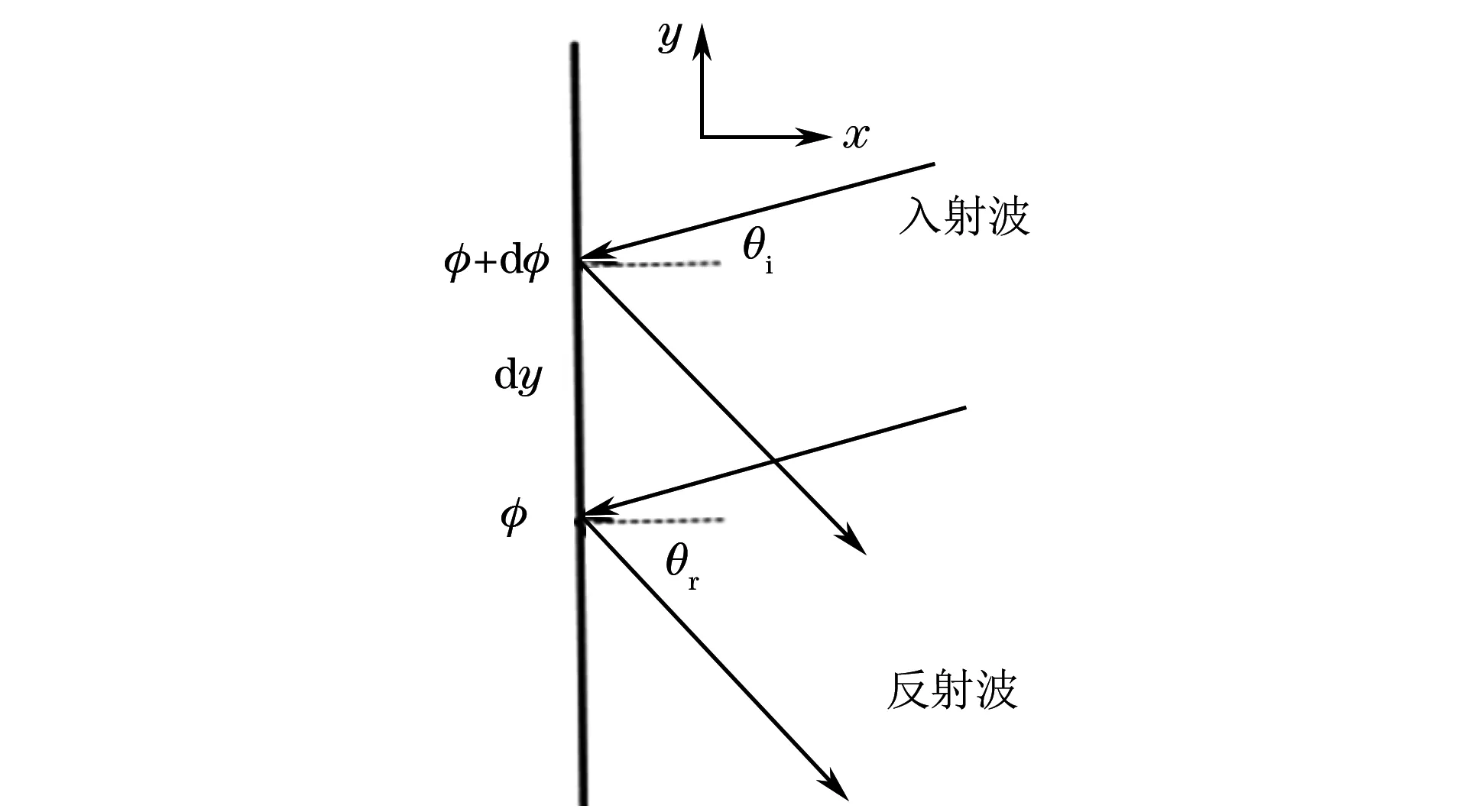
图2 广义Snell定律原理示意
2 声学微结构设计
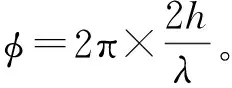
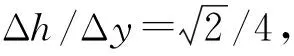

图3 声学微结构示意
3 模拟仿真
3.1 模型建立
采用 COMSOL MULTIPHYSICS(以下简称 COMSOL)多物理场有限元软件进行仿真模拟研究[15]。首先设置一个不带有声学微结构的声场。在COMSOL软件中设置一个半圆形的压力声场,半径设置为7.2 m;在圆心正下方7.2 m处,设置一个长为2.4 m,宽为0.5 m的矩形用以获得平面波声源。将边界条件设置为平面波辐射来模拟无限大空间中的声场分布,将反射界面设置为硬声壁,选中矩形的一条长边,设置其压力为1 Pa。然后对该声场进行仿真,发现声波以垂直方向入射之后会以垂直方向出射。再将上述声学微结构导入到COMSOL中,放置在圆心处,对有声学微结构的声场进行仿真。
3.2 仿真结果分析
图4为带有声学微结构的数值仿真结果,图中中间处为垂直入射的声波,两侧为异常的反射声波。入射波与反射波的夹角约为45°,从仿真结构可以论证上述理论。声波从垂直方向入射,即入射角为0°,通过该微结构成功实现了出射角为π/4的转变。由于声学微结构的对称性,声场在左右两侧π/4的位置上均有反射声波。由此成功论证了广义Snell定律在声学中的应用。
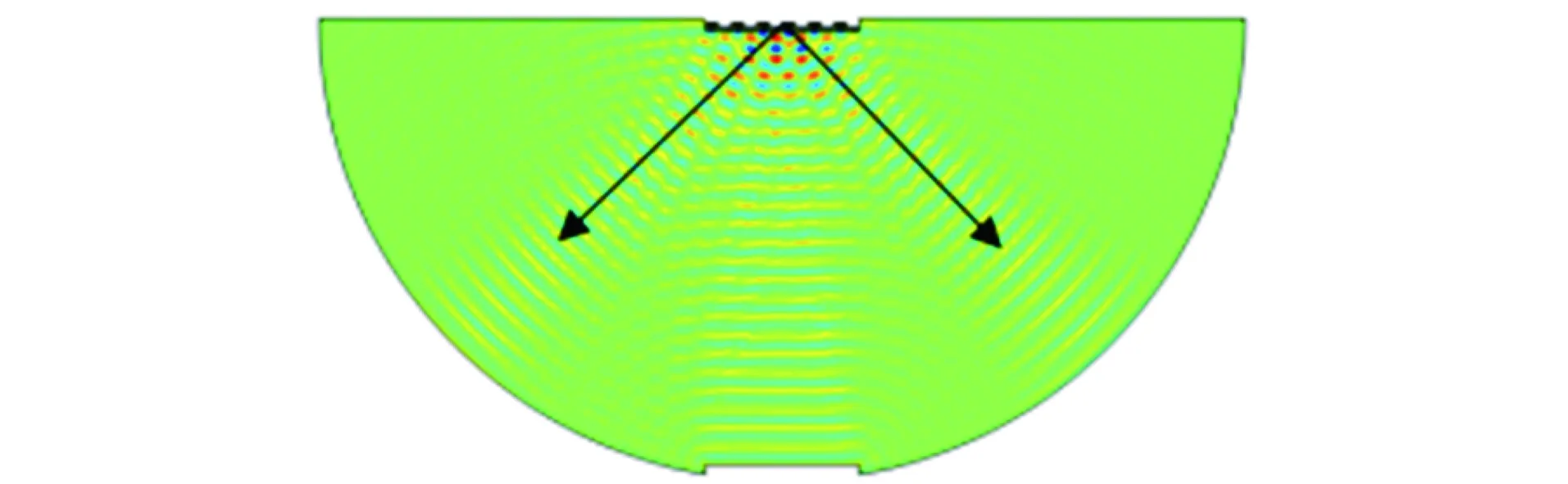
图4 带有声学微结构的数值仿真结果
故可以得出结论,对于给定的声波频率,通过设置凹槽的深度和宽度,便可获得任意的反射角。
4 试验测量
为了验证仿真结果的正确性,在对该声学微结构模型仿真的基础上,利用易拉罐以及3D打印技术对该结构的声反射特性进行了测量。
4.1 易拉罐阵列
由于易拉罐罐口很小,罐身很大,在形状上类似于声学里由小颈口和大腔体构成的亥姆霍兹共鸣器。根据上面的理论推导,利用两种不同大小的同类型易拉罐,其制作材料相同,具有相同的截面积和开口大小。这两种易拉罐的直径均为6.5 cm,大罐子罐身长17 cm,小罐子罐身长12 cm,若想用这两种易拉罐达到上述声学微结构的效果,需要调整声波频率。为了让试验结果更易分辨,使这两种易拉罐产生的相位差为π,则从其罐底反射的声波会干涉相消。声波垂直入射至易拉罐并从易拉罐底反射所产生的相位差为Δφ=2π(h1-h2)/λ=π时,λ=20 cm,空气中声波的速度为343 m·s-1,则该特定频率为1 715 Hz。由于易拉罐的直径为6.5 cm,将3个500 ml的易拉罐和3个330 ml的易拉罐排列为一组,重复3组(即为周期排列结构),此时Δy=19.5 cm,根据计算可得θr=arcsin0.512 8≈π/6。将该模型放置在COMSOL中进行模拟,从仿真结果可看出左右两侧的反射声压在π/6处,如图5所示。然而在垂直出射方向仍存在少部分的反射声场,这是因为结构阵列表面分辨率过低,两种凹槽的π的相位差并不能够完全等效于相位梯度dφ/dy,因此产生的误差相对较大。

图5 易拉罐模型的数值仿真结果
为此采用了易拉罐阵列的方法来更好地解决分辨率过低的问题。试验中采用两种规格的易拉罐各63个,一个周期内长短易拉罐各排成3列7行,共3个周期,阵列总长约为120 cm,高47 cm。同时保证易拉罐的罐口在同一平面内。
声信号的发声装置由信号发生器和扬声器构成,信号发生器产生单频信号驱动扬声器发声,将该装置放于距离易拉罐阵列正前方4 m处,以此来保证声源发出的声波以平面波的形式入射到易拉罐阵列。同时将BK传声器放置在距离易拉罐阵列表面中心位置2 m处,记录声场的声压数据,且每隔10°记录一次。为了减少测量的干扰,试验全程在消音室内进行。
对于该易拉罐阵列反射声场的测量,选择了声波频率为1 700 Hz的声压,其反射声指向性如图6所示。从图6可看出,易拉罐阵列在1 700 Hz的声波垂直入射下,反射声波在33°方向上最为明显,这个试验结果和理论仿真的结果相符合,但从图中可看出在其他方向上也存在少量的反射声波,这是试验的器材过于简单、精确性精准性都不太高造成的。易拉罐阵列试验验证了改变声波反射角的可行性,即可以通过对相位的控制来改变反射声波的反射角度。但是这种易拉罐阵列操作起来不够严谨,而且易拉罐体积大小都是确定的,很难实现任意的反射角,若想在生活中进行实际应用还不现实。

图6 1.7 kHz声波入射下的反射声指向性图
4.2 3D打印板材声学微结构
为了保证试验的准确性和精度,考虑用别的材料来实现这种微结构。结合多种加工技术,充分考虑材料样品的精度,笔者利用3D打印技术制作了更大面积、更为严谨的微结构。该材料样品共由3部分构成,其最小单元也是圆柱形的凹槽。结构最上面的部分由类ABS塑料粉末经过激光烧结而成,上面开有小孔,上盖厚度较薄。中间部分的原材料使用的是20 mm的铝板。结构的最下部分为透明的5 mm聚碳酸酯板,以利于结构内部的观察。3部分的粘合采用的是0.1 mm厚的双面胶,粘合后用重物压合,保证其强度。
该结构的最小单元等同于上述的易拉罐结构,相当于将易拉罐等比例缩小,故仍可实现对某一特定声波频率产生特殊的相位变化,从而获得特定的反射声场,反射角度仍然满足广义的Snell定律。
该结构的最小单元是一个带有圆柱体空洞的长方体。长方体的长宽均为12 mm,高为22.5 mm,圆柱体半径为5.5 mm,高为22 mm,开口口径处的厚度为0.5 mm。对于给定的声波频率8 400 Hz,Δy=12 mm,想要实现90°的相位差,根据公式计算可得θr≈58°。若规定阵列中4个单元为一个周期,则每个单元对应的相位差分别为0°,90°,180°,270°。考虑到0°的相位差等同于声波直接的反射,故第一个单元用平板代替凹槽。其样品结构如图7 所示。

图7 3D打印材料板材样品结构
将该样品放置在消音室中,扬声器放置在距离声学微结构正前方2 m处的位置,距离样品1 m处的位置放置传声器,仍然是每隔10°记录一次数据,记录0°~180°内的反射声压。试验结果如图8所示,从图中可看出频率为8 400 Hz的声波在60°方向反射声压最强,左右两边不对称是板材凹槽倾斜所致。结果与理论计算相符合,验证了该结构的可行性。
5 结语
利用广义Snell定律,通过对反射界面结构的设计实现了反射声波相位的调控,从而在声波垂直入射条件下可得到任意的反射角,通过理论推导与计算,提出了180°相位差的设计模型,成功使得垂直入射声波以45°反射角出射。然后选取大小不同的易拉罐对上述理论进行验证。最后,进一步优化易拉罐的“现成”尺寸,创新地采用 3D 打印技术设计出更精准的板材声学反射镜。试验在专业消声室中对易拉罐阵列样品与3D打印板材样品进行了声场测量,试验的偏振角度与理论预测和数值模拟结果都吻合得很好,既证明了理论的正确性,又论证了多种反射角度的偏转可能性。
该研究意味着通过声学结构可以实现对声波的操控,在噪声控制、医学超声、厅堂声学等领域都有着广阔的应用前景。但目前来看此设计仍存在一些局限性,设计的声学微结构只能对单一频率的声波发生响应,而实际的声音包含很宽的频带,带宽的拓宽将是该项工作未来的研究方向。

