模型转换符号距离场算法实现

乐璐

（四川大学计算机学院，成都610065）

0 引言

电子游戏行业一直致力于在游戏中实现越来越真实的图形效果，但是当前的实时渲染器与用于电影的离线光线追踪渲染器之间仍然存在着巨大差距。近年来人们一直在尝试弥合这一差距，2018 年Wyman[1]在SIGGRAPH 2018 上介绍了实时光线追踪API-DirectX Raytracing。同年，NVIDIA 发布了新一代首款支持实时光线追踪技术的显卡。但是上述实时光线追踪技术并不能完全代替原有的光栅化技术。首先因为渲染最终的画面需要求解渲染方程，而该方程不一定具有解析解，需要通过蒙特卡洛积分求近似解，蒙特卡洛积分法需要用到大量采样数，使用光线追踪计算大量的样本数需要的代价十分昂贵，无法满足追求实时渲染（每秒60 帧）的电子游戏的要求。其次由于光线追踪显卡尚未普及，更多的玩家依旧使用老一代不支持光线追踪的显卡。所以使用其他的下一代渲染方法成为游戏开发的重点，距离场技术就是其中一种可以逼近光线追踪效果的渲染方法。

距离场并不是近几年的概念，早在2007 年，Green[2]利用二维的距离场进行字体渲染，Inigo Quilez[3]利用距离场实现环境光遮蔽（Ambient Occlusion）、阴影（Shadow）等效果，并将之推广开来。在SIGGRAPH 2015 会议上，Wright[4]提出了一种现代的距离场使用方法，显示了距离场理论的可行性，并作为Unreal Engine 中对网格渲染的增强。

符号距离场（Signed Distance Field，SDF）本身是一种十分简单的结构体，Jones[5]定义距离场为“场内任意一点我们知道其到场内任意对象上最接近点的距离”，因此距离场实质上也是表面的一种表示。在数学上，定义符号距离场为：

S 是对象表面上的点的集合，这些点构成对象的整个表面。函数sign 定义为：

广义上讲，符号距离场可以用函数F 表示，以便传递的任意点p 都将返回函数（1）表示的对象距离dist(p)。然后可以将此类函数返回的距离存储为三维纹理，或者作为渲染目的而更常见的三维矩阵。三维纹理的每个网格元素表示从该网格元素到最近的对象表面的距离，因此值为0 的网格元素表示物体的表面，负距离表示该物体的内部，正距离表示物体的外部。从理论上讲，可以使用不同的距离函数生成距离场，包括Chessbord 距离和Euclidean 距离，图1 展示了二维的距离场表示。

图1

在实际的符号距离场渲染中，Euclidean 距离是使用最广泛的距离函数，并且该函数将用于本文所有进一步的实现。本文将游戏渲染中用到的模型作为输入，计算得到该模型的SDF 数据文件，并通过Ray-Marching 的方式验证生成的符号距离场的正确性。

1 算法概述

1.1 算法描述

生成符号距离场的方法通常有两种，一种是利用定义明确的距离函数来为空间中的任意位置生成距离值，对于复杂的形状可以通过布尔运算进行创建，这些距离函数会创建所谓的隐式表面。另一种方法就是由网格（显式）表面转换成距离值，利用三维纹理包含网格曲面存在的整个区域，并且每个网格单元保存该点离最近的网格表面的距离。本文会对上述两种距离场生成方法进行介绍。

1.2 隐式表面转换距离场

创建距离场最简单的方法就是通过距离函数创建，许多基本的几何形状有不同的距离函数，并且由这些基本的几何形状可以组成更复杂的几何图形。距离函数具有不同的计算复杂度，但始终以点作为输入，距离为其输出。最简单的隐式距离函数是球体函数，下述代码片段可以得到球心在原点的球体：

float sdSphere( float3 p,float s)

{return length(p)-s;}

某一点据球体表面的距离就是该点据球心的距离减去球体半径。

常使用布尔运算例如并集、交集等方法将多个基本图形的距离函数组成一个复杂的距离函数来表示复杂的图形，布尔运算具有保持Lipschitz 连续性的特性，因此能够在距离场中依旧保持正确的梯度和距离。

float union( )

float distance1,float distance2

{return min(distance1,distacne2);}

关于各种形状混合的代码可以参考由Mercury 团队做的HG_SDF 距离场库。

创建多个隐式图元之后可以通过查询每个离散网格元素的距离函数，并将这些值与布尔函数组合，使用最终结果的距离值填充三维纹理。由于大多数距离函数计算速度很快，因此可以在运行时执行距离的计算。由于无需保存网格数据，该方法被广泛运用在程序规模很小的图形演示场景[6]中。

1.3 显式表面转换距离场

但是并非所有形状都能通过隐式函数轻松生成，而且由于现代GPU 上高度优化的渲染管线，几乎所有开发的游戏都使用三角网格来表示几何图形。对于游戏中有凹有凸的图形，很难通过隐式函数对其进行模拟。这时候就需要距离转换算法实现网格几何体到距离场表示的转换。

最基本的距离变换算法是蛮力计算，对于每个网格单元计算该单元距离所有三角片元的距离，最短的距离存储在距离场网格单元中。虽然蛮力算法计算代价十分昂贵，但是可以保证结果的正确性，并且该算法可以并行实现，非常适合GPU 计算。本文接下来会详细介绍将现有的模型转换成符号距离场的算法。

2 模型转换符号距离场

蛮力算法是常用的距离变换算法中最简单的方法，首先必须选择距离场网格的范围和每个网格元素之间的距离。选择具有相等尺寸（例如64×64×64）的三维数据集会导致很多空的单元格。通过分析要转换的网格并根据网格的范围缩放尺寸来压缩距离场网格的大小，可以减少总体内存占用。计算完网格大小以后，可以用以下算法计算每个网格的距离值：

Foreach GridCell in DistanceFieldGrid：

Foreach Triangle in Mesh：

Find distance from Triangle to GridCell，save the closest one.

该算法非常简单并且可以很容易通过CPU 并行处理。但是蛮力算法中计算每个网格到三角面片的最近距离时除了如图2 所示需要考虑该点与三角形顶点、边、面的最近距离，还需要知道该网格元素的符号。

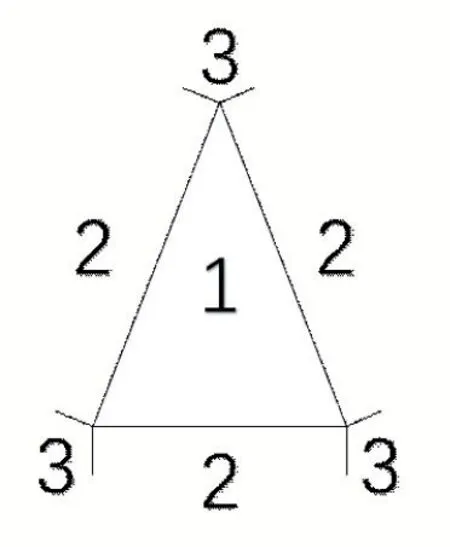
图2 点与三角形距离的三种情况与面最近（1），与边最近（2），与顶点最近（3）

2.1 点到三角形的距离

蛮力算法最重要的步骤是点到三角形面片距离的计算。最接近的点落在三角形的三个特征元素之一上：点、边和面。蛮力算法必须确定网格单元最接近哪个三角形特征，然后计算距离。计算点与三角形距离的方法有2 种，一种三维方法，一种二维方法。本文主要采用三维方法计算点到三角形面片的距离。

（1）三维方法

首先，将网格单元点投影到由三角形创建的平面上，然后将所得的投影点转换为重心坐标，以确定其是否位于三角形面内。如图2 所示，如果位于三角形面上即区域1 的位置，则该点到三角形的最短距离就是网格点和三角形上的投影点之间的矢量的长度；如果位于三角形面外区域2 的位置，则该点到三角形的最短距离就是网格点到三角形边的距离；如果位于三角形面外区域3 的位置，则该点到三角形的最短距离就是网格点到三角形顶点的距离。找到最接近的特征后，计算出网格单元点到该特征的距离，由此得到的最短距离才是该网格元素距离三角面片的正确最短距离。

（2）二维方法

Jones[7]提出将三角形旋转到yz 平面，将点p0到三角形的距离问题由三维转换成二维来解决。该方法需要预计算得到将三角形旋转到yz 平面的旋转矩阵。因为已经将三角形旋转到了yz 平面，点p0(x0,y0,z0)在yz 平面上的投影坐标即为(0,y0,z0)。然后和三维方法一样的检查点与三角形的最接近特征，计算得到最短距离值。因为该算法需要大量旋转，导致距离场中存在许多不准确性，所以本文采用三维计算距离的方法而未采用二维的计算方法。

2.2 符号计算

在计算最短距离之后，需要确定网格的符号，符号表示该网格单元与给定曲面的位置关系，如下函数所示：

由于仅针对闭合曲面定义了内外部，因此会在未闭合的几何体上返回错误的结果。还有一种更简单的定义方式[8]：

其中S 是由一组有向的三角形构成的曲面，n 为任意点q ∈S 的面法线，q 为S 距离点p 最近的点。对于任意集合S 都存在点p 使得sign( p )= sign。因此只要曲面存在方向无需闭合也可以得到符号。

然而在三角形的最接近特征是边缘或点的情况下，如果最近的顶点由网格中的至少三个三角形共享或最近的边缘由两个三角形共享时，有时会产生不正确的结果。如图3 所示，如果算法试图找到最接近的三角形，则两个三角形都符合。两者都能用于符号计算，但是得到的符号相反。可以使用伪法线n'代替三角形的实际法线来解决这种情况。法线n'只是共享最接近特征的所有三角形的法线之和。

上述改进方法虽然能够减轻问题，但是在某些情况下仍然不足。当网格的一个面细分为更多更细的三角形，同时仍共享相同的顶点时，就会出现问题。部分三角形虽然面积很小，但数量多，影响三角形法线总和的方向，如图4 所示。角度加权伪法线可以解决这个问题。除了法线的总和，每个法线还必须通过一个值加权，该值等于连接到最接近顶点的两个边的夹角。对于较小的三角形，具有较小的权重；对于较大的三角形，具有较大的权重。尽管这种符号计算方法在理论上完全正确，但是由于浮点数的不精确，在实际实现中仍存在一些问题。由于浮点数的精度有限，所以相邻的小三角形可能会导致得到的距离略有不同，这将阻止它们的伪法线合并，得到错误的结果。

本文采用Houston 等人[9]提出的基于可见性方法，先集成表面法线信息，然后利用单射线投射奇偶计数的方法来确定网格单元位于表面，内部还是外部。

计算得到最近距离值和符号以后我们就拥有了完整的符号距离场，可以根据符号距离场将原模型重新表示，也可以利用符号距离场计算软阴影等效果。

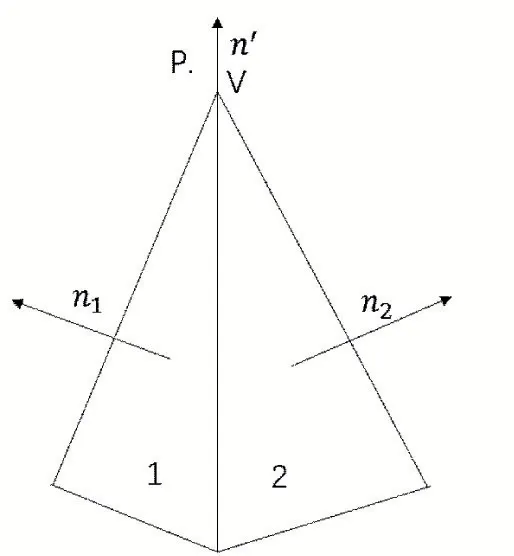
图3 点P最靠近顶点V，该顶点由两个三角形1，2共享

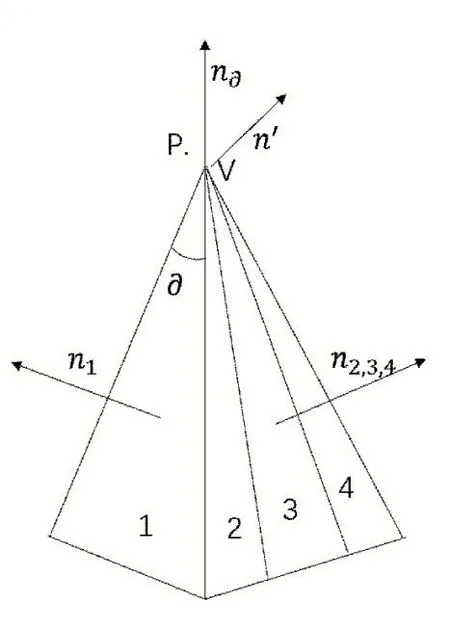
图4 第二个三角形细分成3个三角形2，3，4

3 实验结果

本节将会展示将一个模型转换成SDF 以后，利用Raytracing 的方式查看SDF，验证生成的距离场的正确性。实验设备为：

CPU：AMD Ryzen 3 1200 Quad- Core Processor 3.10GHz

RAM：4.0 GB

System：Windows 10

GPU：NVIDIA GeForce GTX 1050

图5 展示了将鸭子模型和雕塑模型转换成SDF后，利用Raymarching 展示SDF。

图5

表1 展示了生成不同分辨率的SDF 本算法所需要的时间。

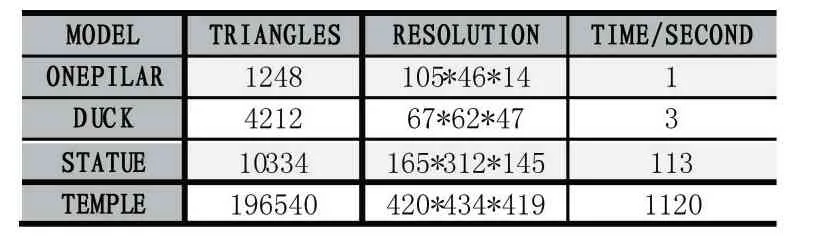
表1 不同模型生成距离场需要的时间

4 结语

本文给出了一种蛮力求解计算符号距离场的算法，通过输入模型文件可以生成符号距离场，并且对生成的距离场利用光线行进的方式进行展示，验证了生成的距离场的正确性，得到了后续可以用于实时渲染效果的距离场。

虽然我们的方法可以得到正确的距离场，但是生成距离场的时间和模型的大小相关，当模型三角面片数目很多时所需的时间代价十分昂贵。尽管可以通过降低分辨率的方式加快距离场的生成，但是会丢失模型细节。在后续的研究中会利用空间加速结构例如KD-Tree 等优化算法，也可以根据上文中提到的利用GPU 并行计算快的特性，加速计算距离场。