一种基于控制参数化方法的柔性关节机械臂的最优PID参数整定方法

吴 昊，郭小龙，谭 元，毛新涛

1.中国航天系统科学与工程研究院，北京 100037；2.北京控制工程研究所，北京 100094;3.四川大学电气信息学院，成都 610065；4.北京轩宇空间科技有限公司，北京 100190.

0 引 言

近年来，随着机器人技术的发展，应用高速、高精度、高负载自重比的柔性机械臂受到航天和医学等领域的关注.由于柔性机械臂在运动过程中关节和连杆具有柔性效应，使得相应的机械结构会发生变形.因此，如果柔性机械臂结构的柔性特征如果不予以考虑，会造成任务执行精度的降低.相对于刚性机械臂而言，柔性机械臂虽然没有高速运动时巨大的惯性力，但是在执行动作过程中产生的振动使它的建模与控制要比刚性臂复杂得多.

针对柔性机械臂的控制，目前主流的控制方法有PID控制[1-2]、逆系统法[3-4]、滑模控制法[5-8]、奇异摄动法[9]和智能控制[10]等.文献[2]提出了一种PID控制结合时变驱动力整形技术(Impulse shaping technique)，实现了对柔性机械臂振动的抑制.文献[1]和[10]采用PD控制方法结合前馈控制实现对期望轨迹跟踪，并使系统在Lyapunov意义下稳定.柔性机械臂的振动具有无穷多个模态，而且在该系统中存在多种耦合.通过将其线性化后，该系统的运动可分解为等效刚体的运动和振动两部分，而前者的运动频率要远低于后者.文献[9]基于奇异摄动法将柔性机械臂系统的数学模型分为快、慢两个子系统，然后对它们分别设计参考模型跟踪和极点配置控制律，从而实现轨迹跟踪和抑制振动.文献[11-12]采用奇异摄动法实现对柔性机械臂的控制.此外，还有基于滑模控制[6]，基于分布参数模型的滑模控制[7]，基于线性模型的滑模控制[5,13]和H∞控制[11].其他方法还包括基于数值优化的控制方法[5,14-15]，智能控制[10,16-17]，非线性控制[6,13]，结合自适应和神经网络的控制[10,18].

PID控制在实际工程中的使用超过90%，是目前在工程应用中最有效的控制方法.因此，本文将采用PID方法来控制机械臂，提出一种最优PID参数整定的方法.首先，将该系统的上升时间、超调量、响应时间等性能指标和各种物理约束如关节电机驱动力矩建模为连续状态不等式约束.建模后，柔性关节机械臂的最优PID参数整定问题转化为含连续状态不等式约束的最优参数选择问题.然后，应用约束转录法结合局部平滑法来处理连续状态不等式约束.经过处理后，连续状态不等式约束可以变为具有标准型的约束[19].但是，问题的可行域会随之发生变化.这个问题可通过文献[19]中所提出的渐近调整相关参数的方法来解决.经过本文方法的处理得到一个标准的最优参数选择问题，这个问题可以用最优控制软件包MISER 3.2来求解[20]，也可以用文献[21]提出Fortran版本求解.数值仿真结果表明，本文提出的方法能有效地达到预定的控制系统性能指标.

本文剩余部分的结构如下：第一节给出了一类柔性关节机械臂的模型以及最优PID参数整定问题的描述.第二节给出了连续状态不等式约束的转化以及如何用转化后的问题求解原问题的计算方法；由于本文是应用基于梯度的算法，所以在第三节推导了代价函数和约束的梯度计算公式.为了验证所提出算法的有效性，第四节进行了相关的数值仿真.第五节对本文的研究进行了一些总结.

1 系统模型和问题描述

本文考虑一类柔性关节机械臂系统[22]，驱动为步进电机，其关节可通过一个具有线性弹性系数K的扭转弹簧系统逼近，如图1所示.

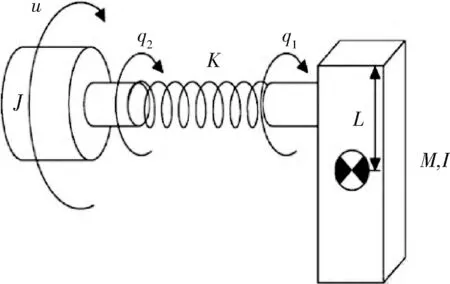
图1 柔性关节机械臂控制结构示意图Fig.1 The structure of a flexible joint manipulator

柔性关节机械臂由如下动力学方程描述

(1)

式中q1和q2分别为关节角度和电机转动角度，I是转动臂的转动惯量，J是电机的惯性矩，K是关节的弹性-刚度系数，g是重力常数，M是臂的质量，L是臂的长度.λ为范数有界的摩擦力，u为输入的控制扭矩.

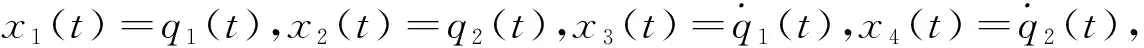
(2)

本文采用PID控制，则式(2)中u可以表示为

(3)

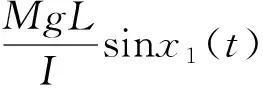
x1(0)=x2(0)=x3(0)=x4(0)=0

为了方便计算，本文引入新的状态变量x5

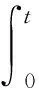
将式(4)带入式(3)可得

u(t)=KP(x1(t)-qd)+KIx5(t)+KDx3(t)(5)

这样可以得到新的状态方程

(6)

本文中使用的步进电机的额定转矩为60 N·m[24]，故此引入如下连续状态约束：

C1(t)=60-|u(t)|≥0,t∈[0,T](7)

考虑超调量限制，本文引入如下约束：

C2(t)=1.16qd-x1(t)≥0,t∈[0,T](8)

考虑上升时间、调整时间和稳定时间等系统性能指标，本文引入如下约束：

C3(t)=x1(t)-δ(t)≥0,t∈[0,T](9)

式中

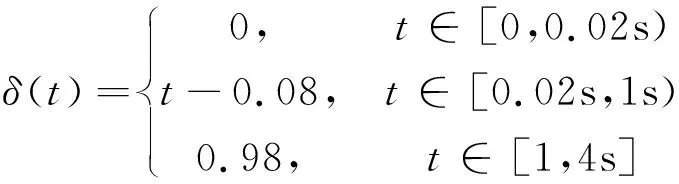
(10)

其中qd=1，T=4s.式(10)表示系统的上升时间为0.9 s，且在1 s内进入稳定状态.

本文考虑恒值参考输入，选取代价函数为

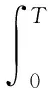
本文所研究的问题如下：给定柔性关节机械臂系统(6)，选取式(5)中KP,KI,KD使得代价函数(11)最小，且满足约束(7)～(9).

2 连续状态不等式约束函数的求解

式(7)～(9)为连续状态不等式约束，是最优控制中的一类难处理的约束.这是因为该约束在每个时间点上都有一个约束需要满足，所以在整个时间段上有无穷多个约束.本节将采用约束转录法结合局部光滑的思想来处理连续状态不等式约束(7)～(9).首先，注意到连续状态不等式约束(7)～(9)可以等价为：

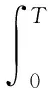
由于上式不可微，对于i=1,2,3,引入如下的光滑函数:

(13)

其中ω>0.因此，Si,ω可微但可行域发生变化.这个问题可以通过如下的方法来解决.首先，考虑如下约束

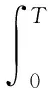
将式(7)～(9)替换为式(14)后，虽然约束可微，但是KKT条件中对于式(14)的约束规范(constraint qualifications)不能满足.因此，本文引入如下约束

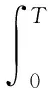
将式(7)～(9)替换为式(15)后，即可满足约束规范.

本文所研究的问题重新描述为：给定柔性关节机械臂系统式(6)，选取式(5)中KP,KI,KD使得代价函数(11)最小，且满足约束(15).称为问题P.

为了给出本文的计算方法，需要如下结论.

引理1.[19]满足式(15)的解也一定满足式(7)～(9).

由于引入式(14)后，问题的可行域发生了变化，因此给出下面的算法对近似问题的可行域进行调整.当ω足够小的时候，可以认为近似问题的可行域与式(7)～(9)足够接近.

算法1. 对于任意的ε和γ,在此问题中取ε=10-1，γ=5ε/16，εmin=10-3.

第一步：由问题P得到最优解k*;

第二步：将最优解k*带入Ci(t),检查约束是否满足；

第三步：若第二步满足转至第五步，否则转至第四步.

第四步：令γ=γ/2,转至第1步.

第五步：令ε=ε/10，γ=γ/10,转至第一步.

当ε≤εmin时算法停止.

由于本文的方法基于梯度计算，故在第三节给出约束和代价函数的梯度计算公式.

备注1. 由于柔性关节机械臂控制问题为非线性问题，单一的PID参数在不同初始条件下难以满足系统所有的性能和条件约束.所以，对于不同范围的初始条件可用文中的方法整定出相应满足约束的PID参数.然后在实际应用中对于不同的初始条件可切换相应的控制参数使其满足特定的性能和条件约束.

3 代价函数和约束的梯度公式

在本节给出代价函数和约束的梯度计算公式.

定理2. 代价函数的梯度公式为

式中k=[KPKIKD]，H0(t,x(t),k,φ0(t))为哈密尔顿函数.

H0(t,x(t),k,φ0)=((x1(t)-qd)2+

f为式(6)的右端项，φ0(t)为下面方程的解，

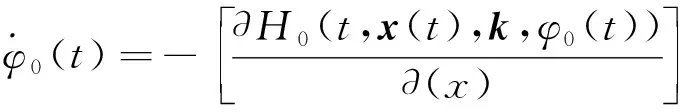
其边界条件为

φ0(T)=0(19)

定理3. 连续状态不等式约束函数的梯度公式为

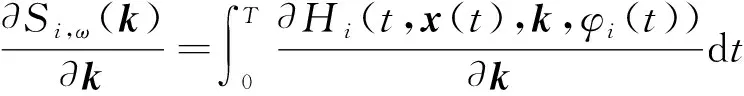
式中Hi(t,x(t),k,φ0(t))为哈密尔顿函数.

Hi(t,x(t),k,φ0(t))=

f为式(6)的右端项，φi(t)为下面方程的解

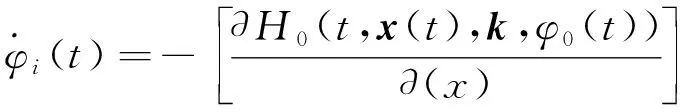
式中i=1,2,3,其边界条件为

φi(T)=0,i=1,2,3(22)

定理的证明类似文献[19]中的定理5.2.1，因此略去定理的证明.通过第二节的处理，最优参数选择问题转化为一个非线性规划问题求解.根据定理2和3，采用标准的非线性规划算法，可以来求解.例如，序列二次规划(SQP).

4 仿真校验

为了验证算法的有效性，本节将采用所提出的算法进行数值仿真.在本文中，跟踪信号选取为单位阶跃信号.采用最优控制计算软件MISER 3.2[20]计算求解，其核心算法为序列二次规划.该系统参数为K=986 (N·m)/rad，I=0.98 kg·m2，J=1.02 kg·m2,M=0.21 kg,L=0.12 m，g=9.8 m·s-2.带入计算KP=59,KI=0.14,KD=11.

当干扰λ=2π-0.28tsint时得到系统响应如图2～图3所示.

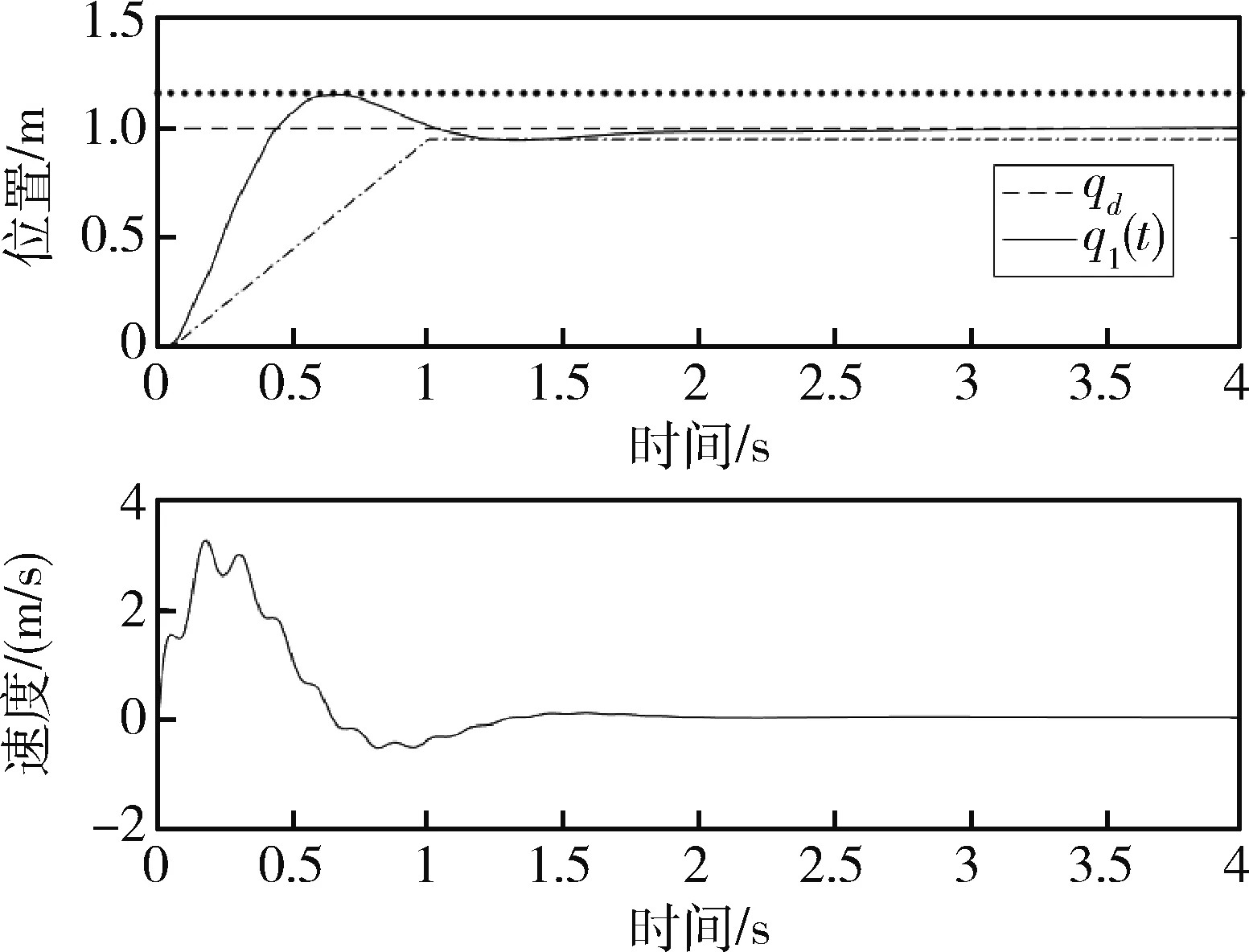
图2 存在干扰时机械臂位置和速度Fig.2 Position and speed of robot arm in responsewith interference

图3 存在干扰时电机力矩控制输入Fig.3 Control inputs of robot arm with disturbance

由图2观察可知，系统的响应满足约束(8)和(9).由于柔性机械臂的特性，机械臂的速度的略有波动.由图2观察可知，控制输入都小于60 N·m，因此满足式(7)的约束.当干扰λ=0时，得到系统响应如图4和图5所示.同样都满足所有约束条件.相比存在干扰的情况，系统响应更为快速.

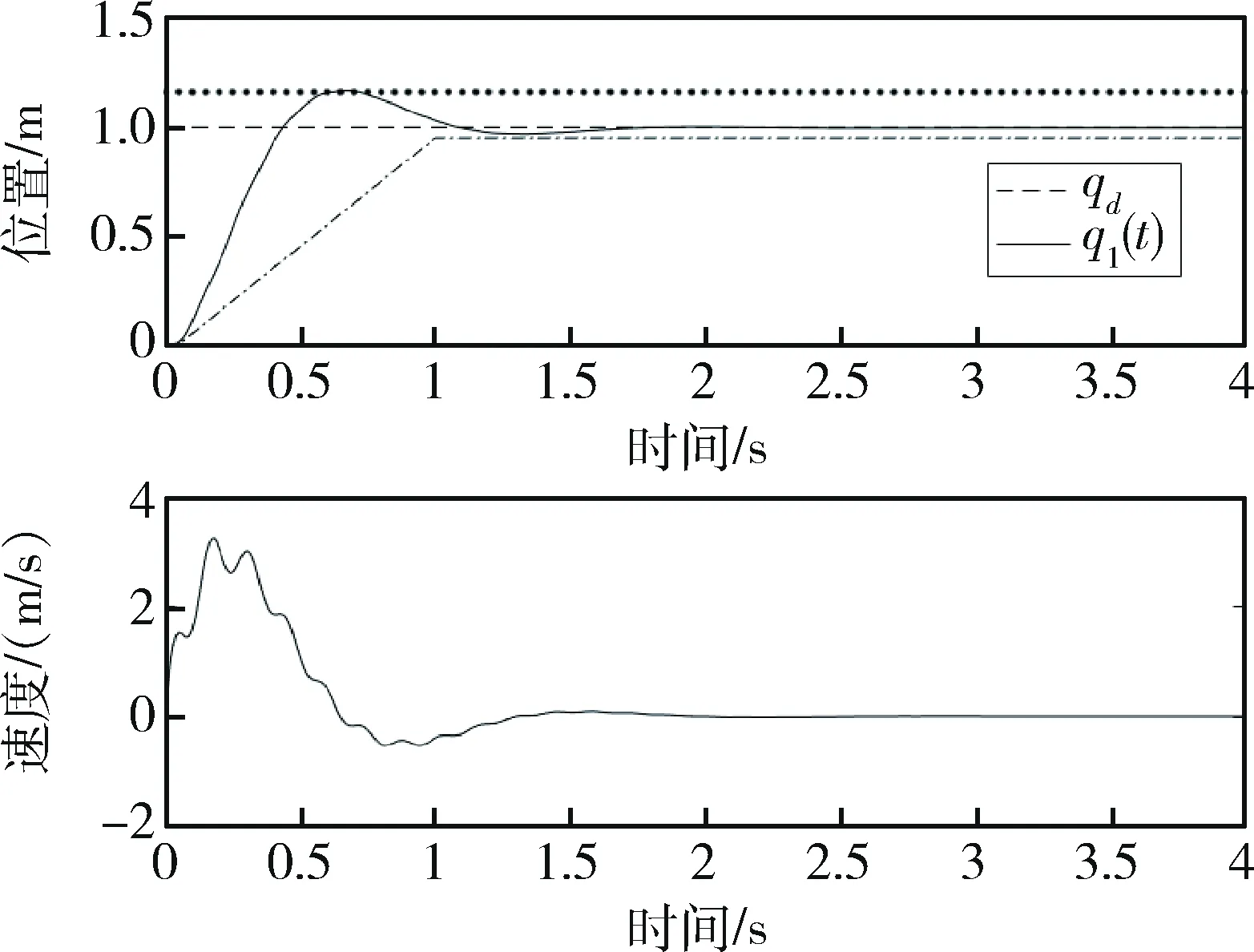
图4 无干扰时机械臂响应时位置和速度变化情况Fig.4 Position and speed of robot arm in responsewithout interference

图5 无干扰时电机力矩控制输入Fig.5 Control inputs of robot arm without disturbance

通过数值仿真结果表明本文提出的机械臂最优PID参数整定方法有效性和可靠性.对比在文献[22]中提出的迭代学习的柔性关节机械臂鲁棒输出跟踪的方法和文献[29]提出的基于奇异摄动理论的自适应鲁棒控制柔性关节空间机械臂的方法，考虑了系统的约束，有更好的应用价值和较好的控制精度.尽管现在许多先进的控制方法在理论上可以对此问题进行比较精确的控制，但是由于其复杂性和不易实现性限制了其更大化的应用.相反，PID控制计算实现都较为简单，可以实现较好性能，且具有一定抗干扰性，所以相比现有方法本文提出算法具有较大的使用价值.

5 结 论

本文提出了一种基于控制参数化的柔性关节机械臂的最优PID参数整定方法.通过约束转录法结合局部光滑的思想，可以把最优PID参数整定问题转化为数学中的非线性规划问题来进行求解.数值仿真结果表明本文提出的最优PID参数整定方法对于柔性机械臂的控制是有效性的，并且具有一定的抗干扰能力.