“以形解数”在小学数学教学中的应用

河南省焦作市解放区实验学校 刘媛媛

“以形解数”是“数形结合”思想中的一个重要方面，在小学数学的“数与代数”领域中应用较为广泛。在教学过程中，如果能够适时地利用直观的“形”来帮助学生理解抽象的“数”，使抽象问题形象化、复杂问题简单化，就能够为学生消除不少学习中的困惑，同时促进学生抽象思维能力的发展。以北师大版小学数学教材为例，依据学生在不同年龄阶段接受能力的差别，教师可以在数学教学过程中有目的、有计划、循序渐进地渗透“以形解数”思想和方法，充分发挥“以形解数”在小学数学教学中的重要作用，提高教育教学质量。

一、启蒙阶段——适时渗透“以形解数”

小学低年级阶段是学生认识“以形解数”的初级阶段，也是进行“以形解数”教学的重要阶段。直观的“形”无处不在且呈现方式多种多样，有水果、蔬菜、玩具和文具等各种实物；有小棒、计数器等各种学具；还有数线、点子图等直观模型。这些直观的“形”在帮助学生认识数、比较数的大小、体会有关数学概念、理解有关算理等方面发挥了巨大的作用，同时也促进了学生抽象逻辑思维的发展。教师在这个阶段要有意识地把“形”融入数学知识教学中，使学生初步感知“形”的存在。

1.将“形”渗透在数的认识教学中。以数的认识教学为例，教材为学生提供了小棒图、计数器图、方块图、数线等图形作为辅助学习的工具，并在教学安排方面做了系统设计。例如：在一年级学习“100以内数的认识”时，以数小棒为主鼓励学生借助实物认识数，同时以计数器、数线为辅助工具，帮助学生加深对数位、数的大小的理解。在二年级下册第三单元“生活中的大数”的教学中，教材利用计数器帮助学生体会位值概念和“满十进一”的道理，借助“方块”图这一直观的“形”帮助学生体会一千有多大：十“个”小正方体组成一“条”表示十；十“条”组成一“片”表示一百；十“片”组成一“块”表示一千。这样形象直观地让学生感受到了一千有多大，恰到好处地培养了学生的数感。

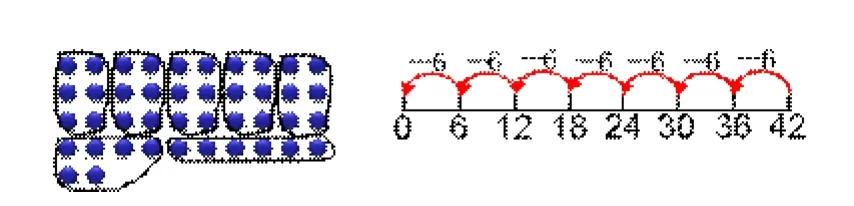
2.将“形”渗透在数的运算教学中。小学阶段数的运算主要是整数、小数和分数的加、减、乘、除以及四则混合运算。在整数的相关运算中，教师教学计算方法多采用点子图、计数器、数线等形式帮助学生理解算理。例如，在“20以内的加减法”教学中，教材引入了小棒和计数器教学。在进行“100以内加、减法”的教学时，又多次使用了数线这一直观图形。由于数线中每一小格代表的数值不同，在表述较大数的加、减运算过程时就会很方便。二年级上册“长颈鹿与小鸟”一课，在探索如何计算“42÷6”时，教材除了介绍用口诀求商的方法，还呈现了圈点子图、画数线图的思考方法（如下图）。这样不仅有利于学生对算理的理解，还有利于沟通除法与减法、除法与乘法之间的内在联系。

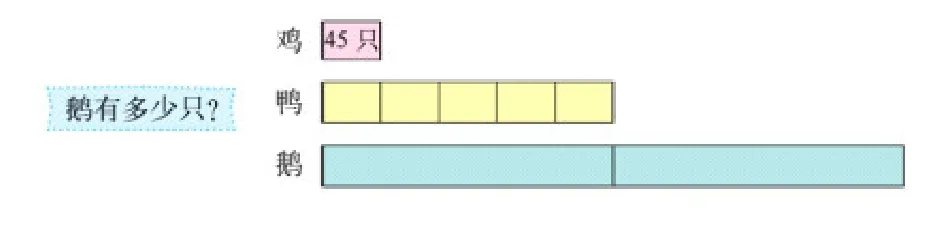
3.将“形”渗透在理解数量关系的教学中。有时候略微复杂的数量关系令学生难以理解，如果能借助于“形”，数量关系一目了然。例如在解决“鸡有45只，鸭的只数是鸡的5倍，鹅的只数是鸭的2倍，鹅有多少只？”这样的问题时，就可以引导学生画出条形图帮助理解题意，理清三者之间的数量关系。鸡是单倍量，画出一个小长方形表示鸡的数量；再画出表示“鸭是鸡的5倍”的长方形；最后画出表示“鹅是鸭的2倍”的条形图（如下图）。这样借助“形”很轻松地帮助学生理解鸡、鸭、鹅之间的倍数关系，列出连乘算式解决问题。

4.将“形”渗透在解决问题教学中。一年级教学中有道习题“在队伍中从前面数小华排第3，从后面数小华排第4，这条队伍一共有多少人？”如果只看信息中的数据，学生很容易就列式3＋4＝7（人），这时教师如果引导学生画图○○△○○○，用△表示小华，那么问题就化难为易，学生很容易明白多算了一次小华，应该是3＋4－1＝6（人），得出正确答案。分析问题时采用○或△等图形来代替实物，可以使抽象的代数知识形象化、简单化，更易于学生理解。

二、形成阶段——适时揭示“以形解数”

渗透“以形解数”思想是提高数学教学效果的基础，随着年级的逐步深入，学生积累的相关的知识经验增加了。当“渗透”到一定程度时，教师就可以适时揭示“以形解数”这一思想方法的内涵，使学生对这一思想有初步理解，这是学生理性认识的开始。在数学教学中常常遇到比较典型的数学案例，对于掌握这些知识，不少学生存在着盲区，如果教师帮助学生加以分析，借助“形”来揭示其中的道理，就能使问题迎刃而解。

案例1：在讲解小数意义时，将组成小数的每一部分分解成若干个面积图形。在操作时，让学生把画有100个小方格的正方形纸按照10个一条的要求剪成10条（每条表示0.1），再让学生把其中的1条剪成10个小正方形（每个小正方形表示0.01）。两人一组开展活动，一个学生说出小数，另一个学生将图形摆出来；也可以一个学生先将图形摆出来，让另一个学生说出小数。这时教师一定要放慢节奏，引导学生学习“形”与“数”相互转换的方法，感受“以形解数”思想的直观与便捷。

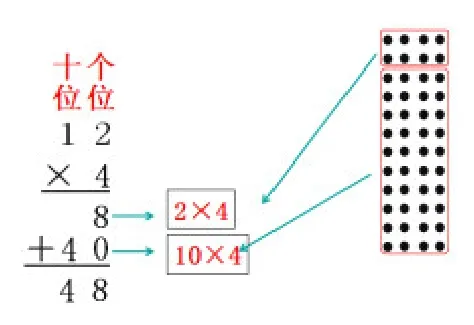
案例2：在教学整数乘除法的计算方法时，采用以点子图为主、示意图为辅的教学模式。以三年级上册“蚂蚁做操”一课为例，这节课主要探索并掌握两、三位数乘一位数（不进位）的计算方法。在教学时将情景图中的一只只蚂蚁抽象成一个个的点，形成点子图。借助点子图这一直观图形，帮助学生更好地理解乘法竖式的计算过程和算理。（如图）

三、应用阶段——强化升华“以形解数”

美国心理学家斯金纳说过：“行为之所以发生改变，是由于强化的作用。”学生获取有效的学习离不开强化训练。当然，强化并不等同于机械性练习。

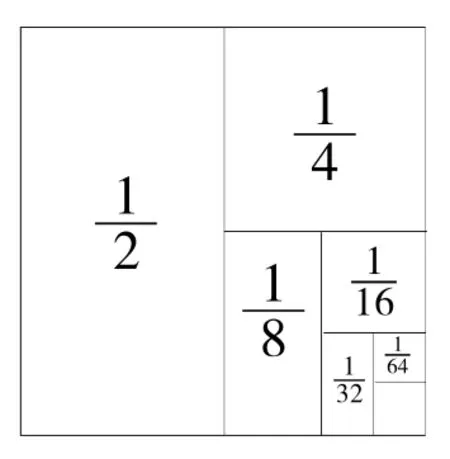
到了小学高年级，教师有意识地强化应用“以形解数”这一思想方法，启发学生去思考、发现，找出一般规律之后通过归纳、总结得到认识升华。此时，学生不仅知道用什么“形”去解决问题，还能在此基础上逐步学会灵活运用。例如一道六年级的典型习题：“一杯橙汁，小明第一次喝了半杯，第二次又喝了剩下的一半，这样每次都喝了上次剩下的一半，六次一共喝了多少橙汁？”，此题可以直接计算1/2+1/4+1/8+1/16+1/32+1/64即为所求,只是计算起来颇为麻烦。这时如果启发学生先画一个正方形，假设这个正方形就是一杯橙汁，那么由下图可知1-1/64即为所求，借助图形，学生一看即知。

综上所述，“以形解数”是一种思想方法，想把它真正地纳入到学生的认知结构中，需要一个循序渐进的过程。通过采用“渗透———揭示———强化”三部曲的渐进式教学过程，让学生逐步感知、理解“以形解数”思想，并逐步学会灵活运用“以形解数”思想方法解决实际问题，是我们教育科学研究的目的。