运载火箭射击方位角计算方法研究∗
(大连91550部队 大连 116023)
1 引言
射击方位角又称瞄准方位角,是瞄准方向与天文北在发射点水平面上投影的夹角,定义由天文北(大地北)顺时针方向旋转为正[1],是由发射点到目标点经过射击诸元修正后的大地方位角[2]。对于机动平台发射的运载火箭而言,射击方位角随发射点和目标点的变化而不同,其精度直接影响落点的命中经度[3]。射击方位角的确定是运载火箭诸元准备和弹道仿真的重要内容,如果不能准确确定发射方位角,运载火箭飞行仿真也将无法开展。特别是在航区规划过程中,需要不断地调整发射区和落区,仿真建立由发射点到目标点的命中弹道,所以射击方位角的计算显得尤为重要。
文献[4]在考虑地球自转、目标点和发射点高程差以及气象等影响,利用二次曲线拟合算法,建立了射击方位角的修正计算方法,该方法需要预先开展大量弹道仿真计算,制作复杂的数据表格。文献[5]提出了基于自由段解析解的射击方位角近似算法,其形式复杂,计算精度有限。文献[6]在对弹道导弹诸元准备基本内容、方法进行研究的基础上,综述了三种诸元计算方案及流程,但是没有对具体方法进行介绍。文献[7]利用贝塞尔大地主题解算方法确定战术导弹射击方位角,提升了中心机的实时理论引导精度,但通过文献[1]对射击方位角的定义,发现该方法不适用运载火箭。
本文基于运载火箭标准弹道模型,给出了一种射击方位角迭代计算方法,给出了具体的计算流程和数学模型,解决运载火箭在型号论证、航区规划、性能仿真等工作中对仿真初始参数的需求。
2 射击方位角计算流程
射击方位角的计算受到地球扁率、地球自转的影响,而且还与弹道制导控制规律及弹道形状也息息相关[8]。为了获取准确的射击方位角,必须通过标准弹道落点,不断迭代修正射击方位角,直至满足精度要求,计算流程见图1。具体计算流程如下:
1)依据给定的发射点和目标点,确定大地方位角A0及两点间的大圆弧长度S;
2)若目标点不在运载火箭的最大和最小射程范围内,则停止计算;否则,继续流程;
3)令Azi=1=A0作为射击扇面角迭代初值开展标准弹道计算,计算仿真落点经纬度;
4)计算仿真落点相对发射点的大地方位角Ai,及偏差修正量 ΔAi=A0-Ai;
5)修正量ΔAi或落点横向偏差满足精度要求,则停止计算,输出Azi;否则,继续流程;
6)修正射击方位角Azi+1=Azi+ΔAi,继续迭代计算标准弹道。
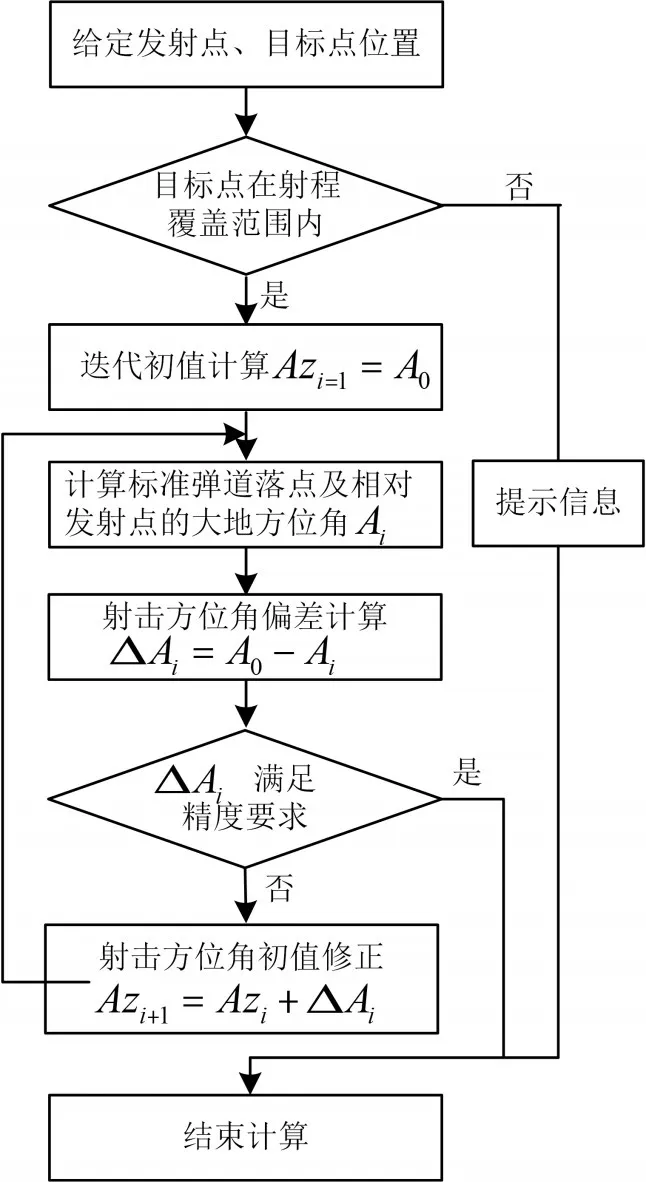
图1 弹道诸元计算流程图
3 射击方位角迭代初值计算
已知地球表面上两点P1和P2,其中 P1点的大地B1、大地经度L1,其中P2点的大地B2、大地经度L2,求解两点间的大圆弧对应的地心角为σ,P1至P2的大地方位角A0,为大地主题反解问题[9]。
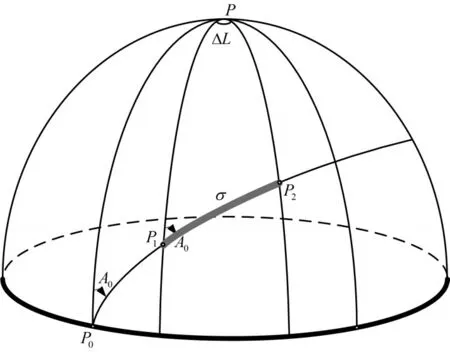
图2 球面关系示意图
根据极球面三角形基本公式[10],对于PP1P2有如下关系:
为确定球面大圆弧对应的地心角σ,首先将式(1)乘以sinA0,式乘以cosA0,并将它们相加结果除以式(3),则得
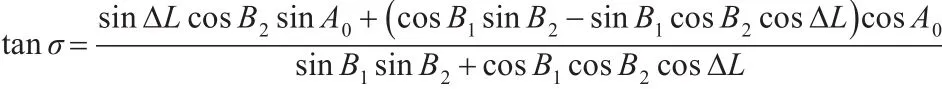
两点间的大圆弧长度 S=Rm⋅σ,其中Rm=6378140m,为地球的平均半径。
4 标准弹道模型
通过简化运载火箭六自由度方程[11~13],在发射坐标系内建立运载火箭三自由度运动方程,见式(4)。

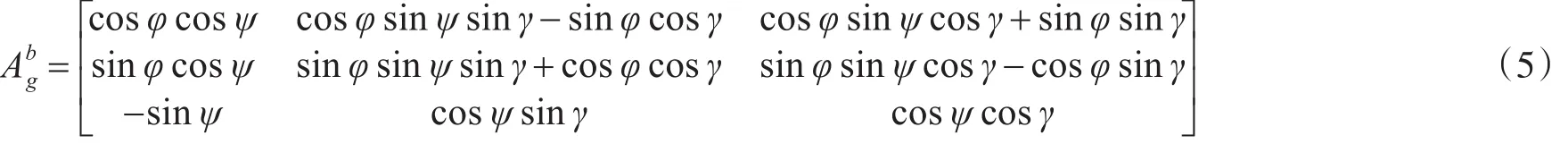
其中,x、y、z为发射坐标系位移矢量;Vx、Vy、Vz为发射坐标系速度矢量;Wx1、Wy1、Wz1为弹体坐标系视加速度矢量;Cx、为气动阻力系数和升力对攻角导数;α、β为运载火箭攻角和侧滑角;Sm为弹体的最大截面积。P为发动机的有效推力,需要根据飞行高度对发动机预示推力数据进行修正。gx、gy、gz为发射坐标系引力加速度矢量;x、˙y、˙z为发射坐标系牵连加速度;、、V˙cz为发射坐标系柯氏加速度,具体计算公式可参见文献。为发射坐标系与弹体坐标系间的方向余弦矩阵,见式(2),其中俯仰角φ取为运载火箭的俯仰飞行程序角,偏航角ψ取为0,滚动角γ取为0。
运载火箭的倾角θ、偏角σ、攻角α和侧滑角β计算公式如下:

5 仿真算例
针对5000km标准射程典型弹道,由于发射点经度对于射击方位角计算影响较小,所以不妨取发射点经度取为0°;发射点和落点高程为0m;发射点纬度分别取 0°、30°、60°、90°;取45°为射击方位角真值间隔;令相临两次射击方位角差值满足不大于10-6的阈度要求。
利用本文算法开展仿真计算,仿真结果与真值的精度和迭代次数见表1。从表中可以看出,即使令迭代控制阈度为10-6,也可通过迭代循环较少次数,获取较高精度的射击方位角。如果控制阈度降低,迭代次数将进一步减少。
6 结语
本文基于给定的发射点和目标点,首先利用大地主题反解算法确定了射击方位角迭代初值,然后通过迭代标准弹道,计算了射击方位角,通过仿真实例验证,该方法只需要迭代几次就能获得较高的计算精度。对于各种制导工具误差、方法误差、中段误差、再入误差等干扰条件下的射击方位角,只需将标准弹道更改为干扰弹道即可。该方法对于弹道仿真具有一定实用价值。

表1 5000km典型弹道射击方位角确定

