Social-Aware Based Secure Relay Selection in Relay-Assisted D2D Communications
Shanshan Yu, Ju Liu, , Xiaoqing Zhang and Shangbin Wu
Abstract: Relay-assisted transmission could effectively enhance the performance of Device-to-Device (D2D) communications when D2D user equipments (UEs) are too far away from each other or the quality of D2D channel is not good enough for direct communications. Meanwhile, security is one of the major concerns for proximity services.The secure relay selection problem for D2D communications underlaying cellular network is studied in this paper. Firstly, we define a relay selection area and derive the closed-form of outage probability in D2D links using a Poisson Point Process (PPP)method. Next, in the defined relay selection area, we propose a secure relay selection scheme for the relay-assisted D2D communication system by exploiting the social relation as a security factor. Simulation results show that the scheme based on social relation can greatly improve the security performance of relay-assisted D2D communications.
Keywords: Device-to-device, social-aware, security, poisson point process.
1 Introduction
With the rapid development of mobile communication technologies, wireless spectrum resources have become unprecedentedly crowded. How to improve the spectrum utilization, the data transmission rate and system security has become a problem to be solved in the future wireless communications. D2D communication is a technology that can improve the spectrum efficiency and channel capacity of the system simultaneously,and thus has been widely studied and applied. Meanwhile, most research work on information security, such as cryptography, watermarking, steganography [Yang, Luo, Lu et al. (2018); Zhang, Qin, Zhang et al. (2018); Ma, Luo, Li et al. (2018)], etc. are the improvement and optimization of related protocols. The security research work in communication focuses more on the physical layer security independently in addition to upper layer protocols. However, most traditional solutions do not fully consider the security of the relay communication and the social relationships between users. To address the issue, D2D cooperative communication technology combined with social networks has emerged. This technology can overcome the shortcomings of traditional D2D cooperative communications and becomes the research hotspot. Additionally, most of related works have considered a relatively simple scenario (i.e., in most cases, a single-cell scenario containing only a single D2D pair was considered). Actually, the spatially distributed base stations (BSs) and cellular users (CUs) in practical scenarios would, to a large extent, impact the accumulated interference of the target users.
For the interference problems caused by D2D communications, the relaying auxiliary communication is an effective method. How to select an optimal relay node from the candidate relays is a major problem in relay-assisted D2D communications. In Ma et al.[Ma, Yin, Yu et al. (2012)], an effective relay selection algorithm was proposed by using the distributed algorithm to select the optimal one after eliminating the inappropriate relay nodes which cause the interferences to the CUs and the D2D users.
Furthermore, the terminal devices used by people constitute a mobile social network. A series of parameters in social networks including social relationships, centricity, and community can reflect the relationship among cellular network users, and utilizing the behavior of people in social networks can help to solve the problem of relay selection in D2D communications. The routing efficiency or total throughput can be improved by utilizing the characteristics of the social network through selecting relays. In order to more effectively improve the communication quality of D2D systems and the relay performance, some scholars have proposed the characteristics of social networks to improve the performance of the communication system.
Zhang et al. [Zhang, Chen and Zhang (2014)] presented a relay selection scheme based on social relations. The optimal relay node is selected by considering the social relationships between the candidate relays and the D2D users. A joint plan of two-step strategy including relay selection and resource allocation was proposed in Zhao et al.[Zhao, Gu, Wu et al. (2016)], and the optimal relay node is selected within the described candidate relay range. Zhao et al. [Zhao, Chai, Chen et al. (2016)] introduced a two-layer game model to discover the optimal relay node for cell-edge users. Chen et al. [Chen,Zhao and Shao (2014)] proposed a relay selection method to maximize the D2D relay link capacity and guarantee QoS for cellular users.
Li et al. [Li, Wu, Hui et al. (2014)] firstly introduced the use of social attributes to improve D2D performance. Authors in Li et al. [Li, Su and Chen (2015)] defined the concept of communication requirements and presented a set of social-aware resource allocation schemes. Zhang et al. [Zhang, Yang and Chen (2016); Cao, Jiang, Chen et al.(2016)] used the grouping idea in Li et al. [Li, Wu, Hui et al. (2014)] to divide users into several large groups to satisfy local services and multicast services, respectively. A concentration mechanism was proposed in Zhang et al. [Zhang, Li, Jin et al. (2015)] to assist D2D pair matching. Li et al. [Li, Giuseppe, Cao et al. (2015)] combined actual geographic factors and social information to present a composite grouping approach. A social awareness program including offline social layer and online social layer for optimizing D2D communication was presented in Zhang et al. [Zhang, Pan, Song et al.(2013)]. Wang et al. [Wang, Chen, Kwon et al. (2014)] proposed an innovative traffic download structure model based on social networks to effectively increase the user’s download capacity.
In this paper, we analyze the relay-assisted D2D communication system model and give the closed-form solution of the outage probability. Then using social relations as a security factor for relay forwarding, we design a social-aware based security relay selection scheme, and compare it with the distance-based relay selection schemes.
2 System model
2.1 Network model
In this section, Fig. 1 shows the network model, the pink triangle presents the base stations, and yellow five-pointed stars are the cellular UEs. The blue solid circles refer D2D transmitter and the red empty circles are the responding receivers. The relays are denoted by solid red square and the small empty black circles are idle UEs which can act as relays.
We assume that the BSs and the conventional CUs are spatially distributed within a given geographical area according to the classical homogeneous Poisson point process (PPP)and of intensities and , respectively. Without loss of generality, an orthogonal resource allocation is assumed to be performed among co-BS CUs for effectively mitigating the intra-cell interference. Furthermore, the D2D transmitters are also distributed according to a homogeneous PPPwith spatial density. Each D2D transmitter has an associated receiver that is randomly distributed around its D2D peer with an average distance.

Figure 1: Network model
When the distance of the D2D pair exceeds, a relay will be applied between the transmitter and the receiver to guarantee D2D link communication. The relays can be idle CUs, idleDUs or other relay devices with locations specified by a homogeneous PPP of intensity . Note that only when the relay is located in the shadow area as Fig. 2 showed,that is both the distances to the transmitter and receiver are less than, the relay will be effective and the relay communication will be established.

Figure 2: Relay selection region
2.2 Outage probability analysis of DUEs
2.2.1 SIR analysis for D2D links
We consider a D2D relay aided underlaying cellular network, the cellular network’s uplink resources are reused for implementing the D2D communications. Without loss of generality, orthogonal resource allocation is assumed to be performed among co-BS CUs.To model the cellular/D2D links as well as the interference links, both the large-scale power law propagation model and the small-scale (e.g., Rayleigh fading) model aretaken into account. Particularly, by considering the transmitter-to-receiver distance and transmit power, the signal power received at a receiver can be denoted by, which is the exponentially distributed fading coefficient between the transmitter i and the receiver j (i.e., Rayleigh fading is assumed), and the standard pathloss exponent. Furthermore, the i.i.d. links are assumed in the above-mentioned model, corresponding to
2.2.2 Interferences analysis for D2D links
The signal-to-interference ratio (SIR) of D2D links is


The interference from the other D2D transmitters is given as

2.2.3 Outage probabilities in DUEs
A SIR model is considered where a message can be successfully decoded at the tagged UE if and only if the SIR of the useful signal is greater than a certain threshold. If the SIR at the tagged UE does not exceed the threshold, the link experiences an outage (here after referred to as SIR outage).
Successful transmission probability of the D2D Links is given as

Because the positions of CUE and DUE obey twomutually independent spatially homogeneous PPP, the Laplace transforms of and can be expressed as [Lee and Haenggi (2012)]:

Therefore, we get the upper bound outage probability of the DUEs when they communicate without any relay:

According to the above derivation, the probability of D2D direct communication outage has been deduced, and the outage probability of D2D aided communication will be derived below. It is assumed that when performing cooperative communication, a typical transmission opportunity selects an idle user as a relay in the surroundings, because D2D is a communication that occurs in a short distance range, so an overlapping area shown in Fig. 2 is selected as a selective area of the relay in this paper. In addition, we adopt the decode-and-forward (DF) relaying scheme.
It is also assumed that the space of the entire system model is A, and there is a selectionareas A (Selection Area, ) according to maximum distance of D2D communicationas shown in Fig. 2, Only idle UEs in the SA may be selected as relay nodes of the D2D communication pair.
Since the location of the idle UEs obeys the spatially homogeneous PPP, we can get the outage probability of the relay-assisted communication by Feng et al. [Feng, Wang, Xu et al. (2014)]:


Since all D2D source nodes transmit in even slots, while D2D relay nodes transmit in odd slots, the interference received at a relay node is from all the co-channel source nodes of other D2D pairs and all the co-channel CUEs that are transmitting in the same radio resources, while interference received at a D2D destination is from all other co-channel relay nodes and all co-channel CUEs.

Substituting (9) into (7), we obtain the average outage probability of a dual-hop D2D link:
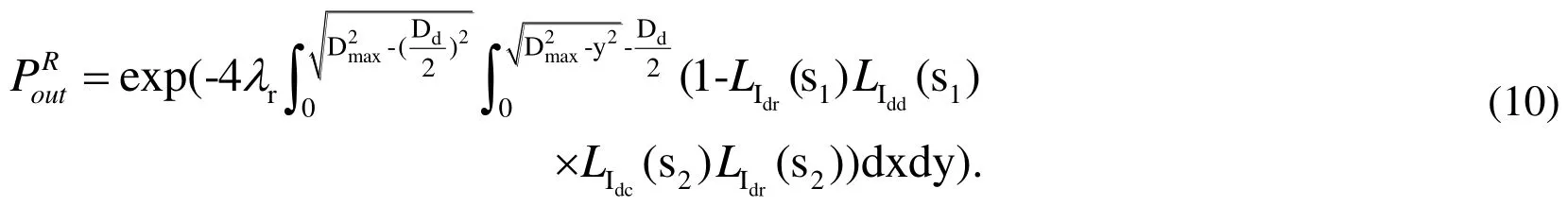
3 Social-aware secure relay selection
The communication security that we will discuss is not physical layer security, but the security based on social relations. In the relay cooperative communication, the most secure relay node is selected for data forwarding based on the consideration of security.The stronger the social relationship between users is, the larger the security of data forwarding is.
In this section, a social-aware based secure D2D cooperative communication relaying scheme is proposed. A distance-based scheme is also introduced in this section for the security performance comparison.
3.1 Social relations
The emergence of mobile social networks has subverted the existing network architecture and added a social layer network architecture based on social relations on the basis of the original physical layer architecture. The relay selection model of the D2D communication system is shown in Fig. 3. The communication model is composed of a two-layer structure of a social layer and a physical layer, and there is a one-to-one relationship between users in the social layer and devices in the physical layer. The presence or absence of a path between users is not related to the physical link of the physical layer,but is determined by the social relationship between users. The social relationship between users is determined by a number of factors, including the relatives and friends among the users, the history of encounters, and the geographical location of the social relationships.

Figure 3: The mapping relationship between the social layer and the physical layer
In this work, we consider that the weight of social-relation is determined by the contact history defined as follows [Feng, Wang, Chu et al. (2015)]:

3.2 Distance-based relay selection
In this part, distance-based relay selection (DRS) strategy is proposed. We have derived the relay region in Section 2. In this relay region, there may be more or less idle UEs, so we will select the most appropriate UE as the final relay. Considering the large-scale fading, we look for the minimum sum of the distances from the D2D transmitter to the relay and the receiver to the relay respectively. The detailed process of DRS is shown in Algorithm 1.

?
3.3 Social-aware based secure relay selection
In this part, social-aware based secure relay Selection (SSRS) mechanism is discussed. In DRS strategy, the optimal relay is not necessarily the safest. In other words, the social relation factors between the relay and the transmitter or the receiver may not high.Therefore, we use the social relationship coefficient as the security factor, and use the product of the security factor of the relay to the transmitter and to the receiver respectively as the evaluation standard. The UE relay that has most strong-relation will be selected as finally relay. The detail relay selection procedure of SSRS is presented in Algorithm 2.

?
4 Simulation results

Table 1: Simulation parameters
Fig. 4 illustrates the security communication factor of different relay selection schemes versus relay selection constraint as well as maximum D2D communication radiusAs mentioned in Li et al. [Li, Wu, Li et al. (2012)], social relations of users obey thedistribution. The physical meaning is that within a certain area, most of the social relationships between users are relatively weak. Only a small part of the users have strong social relations. Thus, we can observe that asincreases, the average security of DRS increases slowly while SSRS increases fast. The reason is that at the beginning a smallresults in a limited number of idle UEs to select where it is hard to find relays;Asincrease, more idle UEs becomes available and relay with strong social relation can be selected, so the average security factor of SSRS becomes higher, but that of DRS still keep smaller than 0.1. The dotted line in Fig. 4 represents the lower idle UEs densitycondition. The same reason for little change of DRS and larger decrease of SSRS.

Figure 4: The different average security communication factor of two relay selection schemes vs. maximum D2D communication radius
5 Conclusion
In this paper, we analyzed relay-assisted D2D communications and gave the closed-form solution of the outage probability. We also proposed a relay selection region simultaneously. Based on this, two relay selection schemes, i.e. DRS and SSRS, were proposed. Using social relations as a security factor for relay forwarding, we analyzed the performance of them. Simulation results reveal that the distance and the social relation play a significant role in the cooperated D2D communication, hence SSRS outperforms DRS in most of the cases. Besides, it was observed that the relay selection region should be set appropriately, i.e., it should be large enough to contain sufficient strong relation idle UEs, while not overlarge to waste time in the selection process.
Acknowledgement:This work is supported by the National Natural Science Foundation of China under Grant No. 61371188, and the National Key R&D Plan under Grant No.2017YFC0803403.
 Computers Materials&Continua2019年2期
Computers Materials&Continua2019年2期
- Computers Materials&Continua的其它文章
- Optimization Algorithm for Reduction the Size of Dixon Resultant Matrix: A Case Study on Mechanical Application
- A Lightweight Three-Factor User Authentication Protocol for the Information Perception of IoT
- Online Magnetic Flux Leakage Detection System for Sucker Rod Defects Based on LabVIEW Programming
- Design of Feedback Shift Register of Against Power Analysis Attack
- Detecting Iris Liveness with Batch Normalized Convolutional Neural Network
- Forecasting Model Based on Information-Granulated GA-SVR and ARIMA for Producer Price Index
