Rational Non-Hierarchical Quantum State Sharing Protocol

Zhao Dou, Gang Xu, , Xiubo Chen and Kaiguo Yuan

Abstract: Rational participants want to maximize their benefits. The protocol with rational participants will be more realistic than the protocol with honest, semi-honest and dishonest participants. We research the rational non-hierarchical quantum state sharing in this paper.General steps of some known quantum state sharing protocol are summarized. Based on these steps, a new rational protocol is proposed. It means that lots of common protocols could be modified to rational protocols. Our protocol is widely applicable. Analyses show that the proposed protocol is rational and secure. It is also all-win for agents. Furthermore,number of deceiving agents is considered to redefine the utilities of agents.

Keywords: Quantum secret sharing, rational protocol, general steps.

1 Introduction

Secret sharing (SS) is one of the most important topics in cryptography. Unfortunately,classical cryptography can usually only achieve provable security or computational security. A possible tool to achieve unconditional security is quantum mechanics.

In 1984, Bennett et al. [Bennett and Brassard (1984)] firstly proposed the concept of quantum cryptography, and designed a quantum key distribution (QKD) protocol. In this protocol, only single particle state is needed. It is easy to perform the protocol. After that,quantum cryptography protocols were widely researched [Jiang, Jiang and Ling (2014); Qu,Chen, Zhou et al. (2010); Qu, Wu, Wang et al. (2017); Qu, Chen, Ji et al. (2018)]. QKD protocols based on continuous variable were also investigated. In 1995, Huttner et al.[Huttner, Imoto, Gisin et al. (1995)] used generalized measurements to design the protocol,and considered photon-number-splitting (PNS) attack. Recently, Gong et al. [Gong, Song,He et al. (2014)] proposed a QKD protocol based on entanglement properties of two-mode squeezed states. The protocol could be utilized to transmit the pre-determined key, which is pretty secure and effective and will become a research focus.

Not only key distribution, SS problem could also be solved by quantum mechanics. In 1999, Hillery et al. [Hillery, Bužek and Berthiaume (1999)] investigated the quantum secret sharing (QSS) protocol based on Greenherger-Horne-Zeilinger (GHZ) state for the first time. Two protocols were given to share classical secrets and quantum secrets (i.e.,unknown quantum states), respectively. The QSS protocol utilized to share quantum secret is also called as quantum state sharing (QSTS) or quantum information splitting(QIS) sometimes. Since quantum state is the most important part in quantum information processing, sharing quantum state is naturally necessary so that no agent can obtain the key secret alone.

From the view of agents’ authority, QSTS could be divided into two parts: nonhierarchical QSTS (NQSTS) and hierarchical QSTS (HQSTS). The latter is usually called as hierarchical QIS (HQIS). Hillery et al.’s protocol [Hillery, Bužek and Berthiaume(1999)] is an NQSTS protocol. In this kind of protocol, all the agents are equal.Concretely, they have the same authority to recover the state. Their measurement results are equally important. This case is similar to the network system [Lu, Wang and Wang(2012); Lv and Wang (2017); Pang, Liu, Zhou et al. (2017); Qu, Keeney, Robitzsch et al.(2016)]. In 2010, Wang et al. [Wang, Xia, Wang et al. (2010)] firstly proposed an HQIS protocol, in which agents are divided into two grades. Agents in different grades have different authorities to recover the state.

There are two points ignored in common QSTS protocols [Li, Zhang and Peng (2004);Deng, Li, Li et al. (2005a); Deng, Li, Li et al. (2005b); Li, Zhou, Li et al. (2006); Li, Deng and Zhou (2007); Liu, Liu and Zhang (2008); Muralidharan and Panigrahi (2008); Xiu,Dong, Gao et al. (2008); Shi, Huang, Yang et al. (2011); Kang, Chen and Yang (2014);Huang (2015); Li, Wang, Zhang et al. (2015); Wang, Wang, Chen et al. (2015); Ramírez,Falaye, Sun et al. (2017)]. On one hand, only the agent who recovers the state (here we denote him as Bobk) will obtain the secret state. So his role is more important than the others’. This role is delegated by authors directly in general. But in fact, it is vital to consider the person who recovers the secret state. On the other hand, the others may deviate from the protocol. In this case, they may deceive Bobkin order to gain more benefits.

Rational protocol is a kind of solutions to solve these problems. Halpern et al. [Halpern and Teague (2004)] investigated a rational secret sharing protocol in 2006. Random numbers are introduced to affect the behaviors of players. The expected rounds of the three-party protocol are. Here,is the probability of each player cooperating.After that, Groce et al. [Groce and Katz (2012)] showed that whenever computing the function is a strict Nash equilibrium in the ideal world, then it is possible to construct a rational fair protocol computing the function in the real world. In 2016, Wang et al.[Wang, Chen, Leung et al. (2016)] investigated the fairness in secure computing protocols based on incentives. New utility definitions are given according to incentives for rational players.

In 2015, Maitra et al. [Maitra, Joyee, Paul et al. (2015)] firstly introduced the concept of rational agent to QSS (to be exact, NQSTS). A rational protocol to share a known quantum state among n agents is investigated. Since the state is known, and can be copied by the dealer, all the agents will obtain the secret state at the end of protocol. In 2017,another rational NQSTS protocol was proposed by Dou et al. [Dou, Xu, Chen et al.(2018)]. This protocol is based on Li et al.’s common multi-party NQSTS protocol [Li,Zhou, Li et al. (2006)]. In Dou et al. [Dou, Xu, Chen et al. (2018)], just like most of QSTS protocols, the state is supposed to be unknown. Hence, only one agent will obtain the state finally. Another difference between protocols in Maitra et al. [Maitra, Joyee,Paul et al. (2015)] and Dou et al. [Dou, Xu, Chen et al. (2018)] is that Byzantine assumption holds in the latter protocol, but fail-stop assumption holds in the former one.However, steps in Dou et al.’s protocol [Dou, Xu, Chen et al. (2018)] are learned from Li et al.’s protocol [Li, Zhou, Li et al. (2006)]. As we mentioned above, there exist numerous NQSTS protocols up to now. Different protocols have different ranges of application. The rational protocol whose steps are learned from the other QSTS protocols should be researched.

In this paper, we follow the work in Dou et al. [Dou, Xu, Chen et al. (2018)], and research the rational NQSTS protocol more deeply. Firstly, we summarize the general steps of aforementioned NQSTS protocols. Secondly, corresponding rational protocols which are based on these steps are proposed. The common protocols whose steps could be summarized as steps in Subsection 2.2 could be utilized in our protocol. The modification is simple and easy to be performed. Our protocol is compatible with common protocols. The agent who recovers the quantum state is not predetermined, or determined by the dealer. In fact, it is elected by all the agents randomly. Thirdly,security, utilities, correctness, fairness, Nash equilibrium and Pareto optimality of our rational protocol are analyzed in detail. Especially, utilities of agents are redefined. In this paper, for any agent, influences of the others’ threat are weighed by the number of threateners. If more agents choose to threaten, then Bobkwill hold less utility. This is more realistic since he needs the help of all the others, and will pay to each of them. This also is an improvement from protocol in Dou et al. [Dou, Xu, Chen et al. (2018)].

The following sections are organized as follow. In Section 2, some preliminaries are introduced one by one. After that, a new rational QSTS protocol is given in Section 3.Later, analyses of proposed protocols are shown in Section 4. Finally, conclusions are given in Section 5.

2 Preliminaries

In this section, some preliminaries are given. Notations of our protocols are listed in Subsection 2.1. Later, general steps of NQSTS protocols are summarized in Subsection 2.1. Hereafter, some basic concepts of rational multi-party computation protocols are introduced in Subsection 2.3. Finally, a simple random election method is described in Subsection 2.4. All of these preliminaries will be employed in the next sections.

2.1 Notations

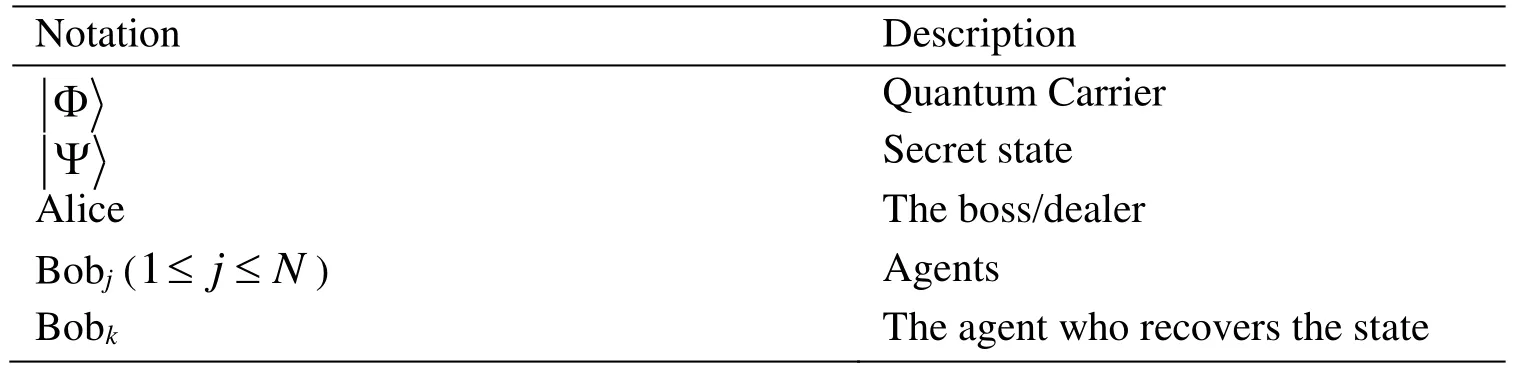
Table 1: The Notations in this paper

2.2 General steps of an NQSTS protocol

We reread abovementioned common NQSTS protocols, and summarize the general steps of an (N+1)-party protocols as follows. Here, eavesdropping checking and some other non-core steps are omitted.

[N-3] According to above measurement results, Bobkperforms corresponding operations to recover.

2.3 Rational multi-party computation protocol

Mathematics provides many tools [Dong, Zhang, Zhang et al. (2014)] to solve practical problems. In game theory, an n-party game could be denoted byis the ith player, his strategy set is. One of his strategy is, so we have. Let, thenis a strategy vector of game. Further,’s utility foris. If he prefers strategy vectorthan, then we say

In addition, for a given strategy vectorcould be denoted as, then

Definition 1 (Strict Nash Equilibrium) [Maitra, Joyee, Paul et al. (2015)]. A strategy vectorin the gameis a strict Nash equilibrium, if we havefor each playerand his any other strategy.

Definition 2 (Pareto Optimality) [Osborne and Rubinstein (1994)]. A strategy vectorin the gameis a Pareto optimality if it is impossible to increase the utility of a player without decreasing any others. In other word, ifthen

2.4 A simple method to randomly elect one player among N players

[E-2] The publishing time of each number will be checked one by one. If a number is not published on time, the player will be disqualified. The other players will restart the election game.

[E-3] If all the publishing times are the same, players can compute. Here,denotes summation modulo N.will be the chosen one.

3 The proposed rational NQSTS protocol

In this section, a new rational NQSTS protocol is proposed. An (N+1)-party common NQSTS protocol could be modified into an N-party rational protocol. The processes are given here. Since processes of different participants are described severally in general rational protocol, processes of our proposed protocol are also shown according to this way.

3.1 The dealer’s protocol

[D-1] The dealer prepares an r-length bit list, in which only one bit is 1. For example,. In the ith round, if, she goes to step [D-2], otherwise step [D-].

[D-2] Then, the dealer prepares enough (aN+a+b)-particle states. She shares them with all the agents. Each agent holds a particles, and Alice keeps the reminding a+b particles.

[D-4] She asks all the N agents Bobjto measure particles in basis. Then, she tells agents to publish the measurement results.

[D-5] She sends the reminding a particles to the elected Bobkvia quantum teleportation[Rigolin (2005); Zha and Song (2007)]. Alice finishes her work.

3.2 Bobj’s protocol

[B-1] In each round, all the agents performbasis measurement on their a particles,and announce the results as the dealer’s claim, respectively. If, they go to step

[B-2] They randomly elect one of them using the random election method. The chosen one, i.e., Bobk, will recover the state afterwards.

[B-3] Bobkperforms some local operations to recover. These operations are related to all the other agents’ measurement results. The protocol is accomplished.

4 Analysis of proposed NQSTS protocol

In this section, security, utilities, correctness, fairness, Nash equilibrium and Pareto optimality of our rational NQSTS protocol are analyzed one by one.

4.1 Security

With the development of computer science, security of data has attracted more and more attention. Security of our protocol is analyzed below.

On one hand, our protocol is based on common NQSTS protocols. Any secure QSTS protocol, which can be generalized to protocol in Section 0, can be modified to a rational version. On the other hand, comparing our rational protocol with common protocols, the only key change is that teleportation is performed between the dealer and Bobk. If a secure teleportation protocol is performed here, this process is secure too.

In conclusion, the security of our rational protocol is equivalent to the original common protocol. If the original common protocol is secure, our rational protocol is also secure.

4.2 Utilities

As is well known, the agent who recovers the state plays a different role from the helpers.His utility is different from the other’s further. Therefore, utilities of Bobkand Bobj() are listed respectively.

Here, COO represents the strategy Cooperating, which means that the agent will choose to cooperate with the others and fulfill the protocol honestly. DEC denotes Deceiving. it denotes that the agent will deceive the others. For example, he may report a false measurement result. REC denotes Recovering, which means that Bobkwill recover the state.Discussions about these utilities are given below. (1) Since he will be punished if he does not pass the check, we have. Further, if he doesn’t pass the check in the ith round, he will be forbidden to participate in the protocol in the nextrounds. The probability of not participating in the sharing is. So we could suppose that(2) Because getting a true state is naturally better than a false one, it is easy to obtain that. (3) A cooperator is not responsible for deceivers’behaviors, so. For the rest of the paper, no differentiation is made betweenand. (4) The motivation of agents choosing to threaten is he may benefit more than to help, so. In summary, we know thatand

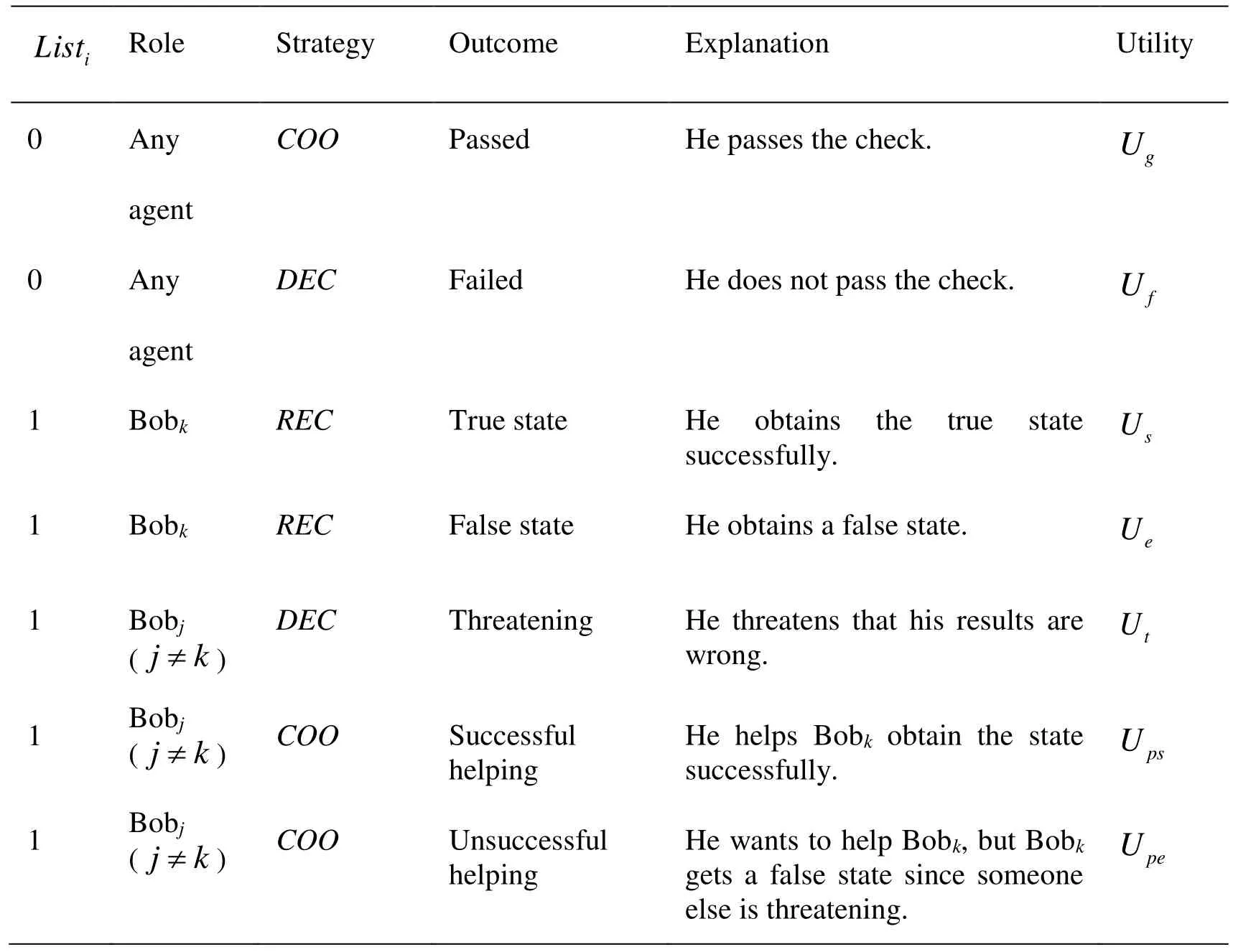
Table 2: Utilities of agents in our rational QSTS protocol

Table 3: Utilities matrix of agents

Next, take the three-party QSTS game as an example, utilities matrix of agents in our protocol could be described in Tab. 3.

4.3 Correctness

Definition 3 (Correctness) [Dou, Xu, Chen et al. (2018)]. A rational QSTS gameis correct if the following holds

for each Bobj’s arbitrary strategy

Theorem 1. The correctness of the protocol holds if all the agents are rational.

Proof. As a rational agent, Bobj() wants to maximize his benefit. If he is chosen as Bobk, he will recover the state faithfully. Otherwise, he will be a helper. In the second case, if he helps Bobkloyally, correctness of protocol will be affected. If he wants to threaten, he will mislead Bobkat first. But if he has obtained expected benefit, he will tell the true measurement result to Bobk. The correctness is also ensured. In one word, the correctness of the protocol holds.

4.4 Fairness

Definition 4 (Fairness) [Dou, Xu, Chen et al. (2018)]. A rational QSTS gameis fair if the following hold

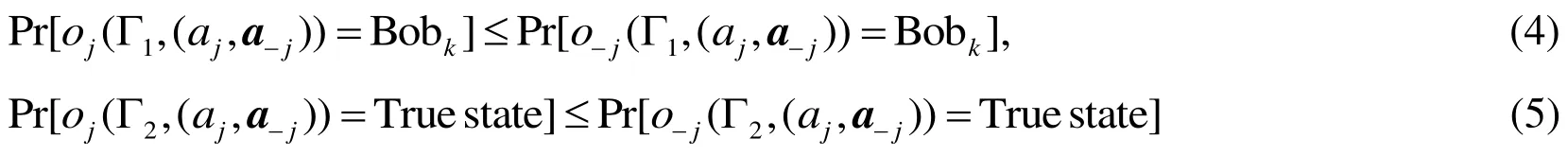
for any Bobj(). Here, the gameis divided into two parts: the random election gameand the sharing game.

Theorem 2. There exist some values ofand r that make the protocol achieve fairness.

Proof. Since each agent chooses a number randomly, entropy ofLet the summation of all the other numbers is. The condition entropy is, too. We also know that. It means that even if N-1 agents colluded except for Bobj, the value of C is still completely random for them. Theprobability of each agent chosen as Bobkis equal. Therefore, the fairness of game is proved.As for the game, any agent will not have incentive to deceive if the utility of DEC is less than that of COO when the other agents’ strategies are fixed. In other word, the inequationneeds to be satisfied.

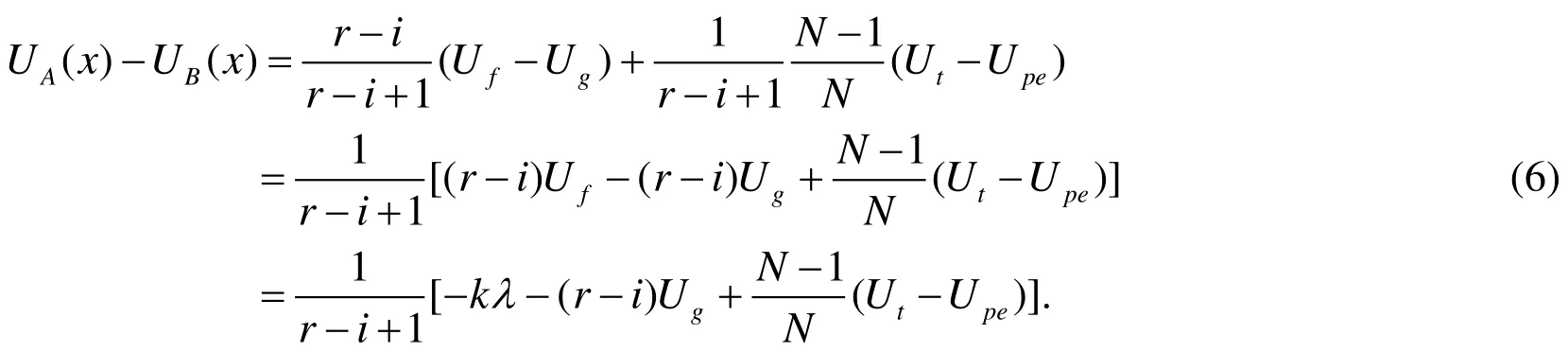
4.5 Strict Nash equilibrium

Theorem 3. There exist some values ofand r that make the protocol achieve fairness.Proof. As the designer of a protocol, we hope that strategy vector (COO, COO, COO)will be the Nash equilibrium. In this case, an agent will choose to cooperate for other agents’ any given strategies. Therefore, the following conditions need to be satisfied:Likewise, we can find some values ofand r to ensure the Eq. (7). The conditions are the same as that in Subsection 4.5. The strict Nash equilibrium of our protocol also holds.

4.6 Pareto optimality

Theorem 4. There exist some suitable coefficientsand r so that Pareto optimality is achieved.

Proof. The utilities of strategy vector (COO, COO, COO) are. In order to make this strategy vector Pareto optimality, we need to ensure the following conditions:

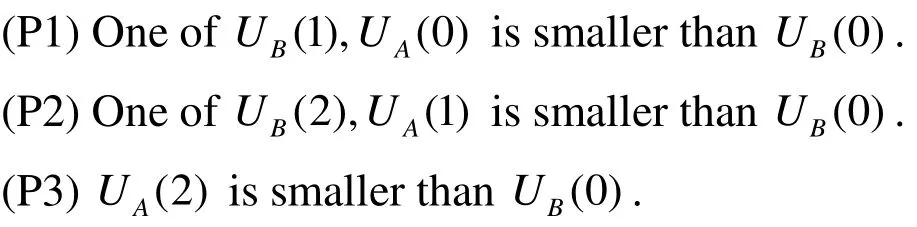
On one hand, in the former subsection, we have showed the conditions ofOn the other hand, from Eqs. (1) and (2), it’s easy to haveand

In summary, the strategy vector (COO, COO, COO) is the Pareto optimality for some suitable r and. Since each agent will choose to cooperate, and is the maximum among utilities, all agents will have maximum utility in this case. In other word, they are all-win.

5 Conclusions

In this work, rational NQSTS protocol was researched. Firstly, lots of NQSTS protocols were restudied. General steps of them were summarized further. Secondly, a new rational NQSTS protocol was proposed, in which steps are learned from general steps of aforementioned protocols. Thirdly, analyses of proposed protocol were given.Particularly, utilities of agents are being redefined by the number of deceiving agents.The results show that our protocol is rational and secure. Besides that, agents will all win in our protocol.

Acknowledgement:Project supported by NSFC (Grant Nos. 61671087, 61272514,61170272, 61003287, U1636106), the Fok Ying Tong Education Foundation (Grant No.131067) and BUPT Excellent Ph.D. Students Foundation (Grant No. CX2018310).