WiBPA: An Efficient Data Integrity Auditing Scheme Without Bilinear Pairings

Chunhua Li , Peng Wang Changhong Sun Ke Zhou and Ping Huang

Abstract: The security of cloud data has always been a concern. Cloud server provider may maliciously tamper or delete user’s data for their own benefit, so data integrity audit is of great significance to verify whether data is modified or not. Based on the general three-party audit architecture, a dynamic auditing scheme without bilinear pairings is proposed in this paper. It utilizes exponential operation instead of bilinear mapping to verify the validity of evidence. By establishing the mapping relation between logic index and tag index of data block with index transformation table, our scheme can easily support dynamic data operation. By hiding random numbers in the integrity evidence, our scheme can protect users’ privacy information. Detailed security analysis shows that our scheme is secure against attacks such as forgery, replaying and substitution. Further experiments demonstrate that our scheme has lower computational overhead.

Keywords: Cloud storage, integrity verification, dynamic auditing, bilinear pairings.

1 Introduction

Cloud storage services are getting more and more attention for such advantages as ondemand, flexible, and dynamic, many individuals and enterprises begin to outsource their growing data to the cloud service providers (CSPs). Meanwhile, they fear that the data will be tampered or leaked by unreliable service providers. Therefore, it is essential to provide a correct and efficient method to verify the integrity of remote cloud data.

Provable data possession (PDP) model [Ateniese, Burns, Curtmola, et al. (2007)] is the first scheme that allows a client to prove the integrity of data stored at untrusted servers without retrieving it. The model generates probabilistic proofs of possession by sampling random sets of blocks from the server, which drastically reduces I/O costs. However, it adopts sequential index number of data blocks to calculate the tag of homomorphism certification, once a block of data is updated all tags are to be recalculated, thus resulting in significant computational overhead. For this reason, PDP can only be used for static data files. Subsequently, Ateniese et al. [Ateniese, Pietro, Mancini et al. (2008)] construct an efficient and provably secure PDP (SPDP) technique based on symmetric key cryptography, which can support such dynamic operations as block modification, deletion and appending. Based on SPDP, Erway et al. [Erway, Papamanthou and Tamassia(2009)] present a definitional framework and efficient constructions for dynamic PDP(DPDP), which supports full provable updates to stored data, including block insertion,deletion, modification and other update operations. But, a large amount of auxiliary information is required in each verification process, which results in a large computational and communication cost.

Based on the idea of PDP, many auditing schemes have emerged in recent years. Wang et al. [Wang, Wang, Ren, et al. (2011)] enable public auditability and data dynamics for storage security by manipulating the classic Merkle Hash Tree construction for block tag authentication. Zhu et al. [Zhu, Ahn, Hu et al. (2013)] construct a dynamic audit service based on the fragment structure, random sampling, and index-hash table, however, the update operation is inefficient, especially insertion and deletion operations. Yang et al.[Yang and Jia (2013)] propose an efficient privacy-preserving auditing protocol, which support the data dynamic operations and batch auditing. Shen et al. [Shen, Shen, Chen et al. (2016)] propose an efficient public auditing protocol with global and sampling blockless verification as well as batch auditing, in which a novel dynamic structure is introduced, which consists of a doubly linked info table and a location array. Sookhak et al. [Sookhak, Yu and Zomaya (2018)] present a remote data checking method on the basis of algebraic properties of the outsourced files for big data storage, which uses a new data structure called Divide and Conquer Table to proficiently support dynamic data for normal file sizes.

To prevent server from disclosing user’s privacy, Wang et al. [Wang, Chow, Wang et al.(2013)] utilize the public key based homomorphic authenticator and random mask technique to achieve a privacy-preserving public auditing for secure cloud storage. Cai[Cai (2013)] constructs a comprehensive auditing system for cloud data integrity auditing(CDIAS), which supports public and batch auditing as well as privacy protection. Tian et al. [Tian, Chen, Chang et al. (2015)] propose a dynamic hash table (DHT) based public auditing for secure cloud storage, which also supports privacy preservation and batch auditing by employing the aggregate BLS signature technique.

Most of the above schemes exploit bilinear pairing to verify the integrity of remote data.It is well known that the computational cost of bilinear mapping is huge, it will lead to the delay of verification. In order to reduce the high computational cost, Dong et al.[Dong, Gao, Shi et al. (2014)] propose a certificateless blind signature scheme without bilinear pairing, which solves the problem of certificate management and key escrow existed in the identity-based public key cryptography, thereby greatly reduces the cost of computation and storage. Zhao et al. [Zhao, Ren, Xiong et al. (2015)] present an integrity verification scheme for cloud data without bilinear pairing. This scheme needs a believable TPA to audit cloud data. Wu [Wu (2017)] proposes an improved public auditing protocol without bilinear pairing and analyzes some security properties, such as correctness, unforgeability, and privacy protection. This scheme simplifies the auditing algorithm and has lower communication and computational overhead. However, dynamic data auditing is not mentioned in this paper which only discusses static data auditing. As we all know that cloud services are not only limited to archive or backup data, dynamic data operations are very frequent in cloud environment, thereby it is necessary for any scheme to support dynamic data verification in a cloud environment.

In this paper, we present an efficient integrity auditing scheme for cloud data without bilinear pairing. We adopt exponent operation instead of bilinear pairings to verify the validity of evidence during the process of verifying. By establishing the mapping relation between logic index and tag index of data block with index transformation table, our scheme can easily support dynamic data operations, include insertion, deletion,modification and all other update operations. By hiding random numbers in the integrity evidence, our scheme can protect users’ privacy information. Due to not using complex bilinear operation, the efficiency of auditing is greatly improved. Detailed security analysis shows that our scheme is secure, it can resist such attacks as forgery, replaying and substitution.

Paper organization is as follows: Section 2 introduces some backgrounds about audit model and mathematical knowledge. Section 3 describes our scheme in detail. Section 4 gives the detail security analysis. The analysis of performance and function is shown in Section 5. The conclusion is drawn in Section 6.

2. Preliminaries

2.1 System model

In this paper, we adopt the common three-party auditing model for data verification(shown in Fig. 1) [Jin, Jiang and Zhou (2016)], which contains the following three parts:user, cloud server provide (CSP), and the third-party auditor (TPA). A user can be a data owner as well as a data user. As an owner, he first divides file into some data blocks and labeled them before outsourcing them to the remote server, at the same time, access control policy for data is specified and attached to the metadata. CSP is often supposed semi-trusted in cloud environment, it may remove or tamper user’s data for his own interest. TPA acted as a moderator trusted by both CSP and user. When TPA receives user’s requests to audit, it will send a challenge to the server, the server then returns integrity evidences to the TPA, TPA then verifies the integrity of data based on the information of evidence and request using bilinear mapping or other algorithms.Meanwhile, TPA can arbitrate in case of any conflict between CSP and user.

2.2 Bilinear map

A bilinear map is a map e: G1×G2→GT, where G1and G2are two Gap Diffie-Hellman groups of prime order p, GTis another multiplicative cyclic groups with the same order.A bilinear map has the following three properties [Dan, Lynn and Shacham (2001)]:

● Bilinear: For all g1, g2∈G and,.

● Non-degenerate: e(g1, g2)≠1, where g1, g2are generators of G1and G2.

● Computable: For all,can be computed in an efficient algorithm.

The bilinear pairs can be constructed by the Weil on the elliptic curve or the Tate pair.

2.3 Aggregate signature

The aggregated signature [Velte, Velte and Elsenpeter (2009)] is a digital signature,which can compress multiple single signatures into one signature and achieve batching.For example, a linear combination value is calculated based on the content of multiple data blocks when it needs to generate integrity evidence, further, an aggregate tag is calculated according to the corresponding tag of each data block. Compared with individual verification for each signature, aggregated signature significantly reduces the computational cost and communication overhead of transmitting integrity evidence.

3 The proposed auditing scheme

3.1 Design goals

An integrity verification scheme in cloud needs to meet the following objectives:

● Storage correctness: only the user's data is complete, TPA will pass the check of data integrity.

● Privacy protection: TPA cannot obtain the real content of user’s data during the process of verifying.

● Dynamic auditing: permitting user to add, delete or modify his data during auditing.

● Security: at least against forgery attack, replay attack and replace attack from CSP.

● High efficiency: as low computational overhead as possible to improve its actual application services.

3.2 The proposed auditing scheme

The process of auditing consists of three stages: installation, verification and dynamic update, as well as eight steps.

Before we begin to describe the detail steps, it is necessary to first define some parameters. Suppose G is the multiplicative cyclic group with prime order p, g is the generation element of G, H(▪) means the mapping function from (0,1)*to Zp, namely, H(▪)is the hash function of G →Zp.

Key generation algorithm, used by the user to obtain his public key and private key. A user randomly chooses an element x (x∈Zp) to compute, then the user’s private key sk is generated byand the public key pk is gotten by.

Tag generation algorithm, used to split file into some data blocks and generate a tag for each block. Suppose the user file F is divided into n blocks, then F can be denoted as. The user randomly generates a file name for file F from Zp, then to calculate the tag σ for each data block as follow:

Where Biis the index of a data block, which represents the actual order of the data block miin the whole collection F{mi}1≤i≤n, Biis initially set to i. Viis the current version number of a data block with an initial value of 1. Tiis the current timestamp which is used to calculate the authentication tag for a data block mi.

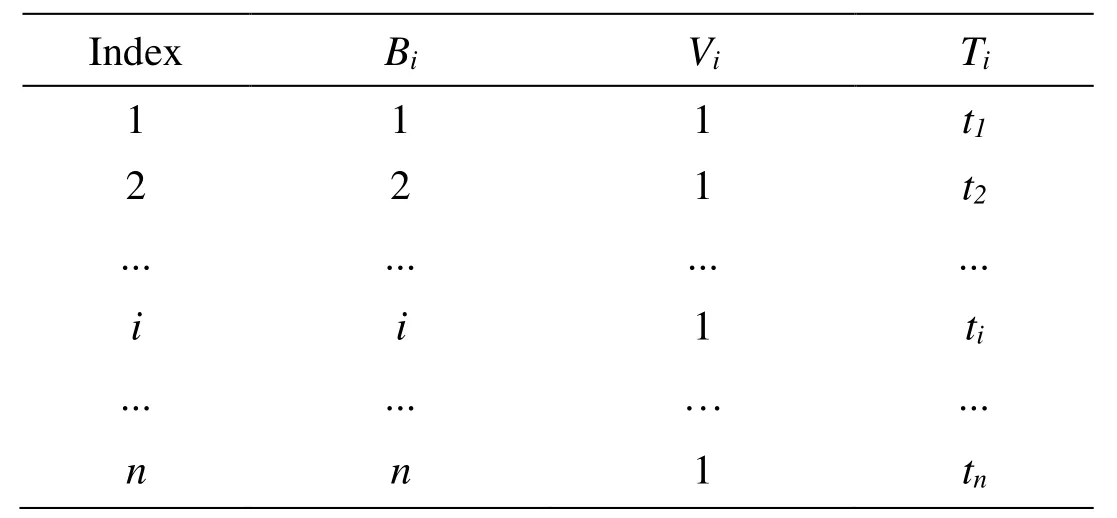
Table 1: The initial index transformation table

Challenge algorithm, used to generate challenge information when audit request is submitted to the CSP. TPA randomly generates c numbers from 1~n, the i-th random number is marked with si’ which represents the logical index number of data block to be challenged. Let. Based on the ITT, TPA queries block index number sicorresponding to each logical index number, and then forms a collection I,. For any, generating a random number vi() corresponding to si. Then, TPA sends the challenge informationto the CSP.

Evidence generation algorithm, used to generate the integrity proof. After CSP receives the challenge information, it generates a random number r (), and calculates the following parameters for verification:

Finally, CSP sends an evidenceto TPA which will use evidence to verify whether the data stored on the server is intact or not.

Evidence validation algorithm, used to verify the correctness of the integrity evidence sent by CSP. Specially, we adopt exponent operation instead of bilinear pairings to check the validity of evidence. According to the challenge information viand evidence P, TPA can verify whether the exponent operation described in Eq. (3) is true or not:

If the equation is true, it can state that user’s data is correct, otherwise user’s data may be tempered.

It is used to generate the update data and send request to deal with the operation. Here, k represents the logical position where data is updated, cmd is the type of dynamic data operation, including insertion, deletion and modification. We will use the modification operation as an example of how to conduct the data update.

This algorithm is used to update the content of ITT after TPA receives the index update request. The changed ITT for modification operation is shown in Tab. 2. If executed successfully, it will output “success”, otherwise, will output “fail”.

This algorithm is used to update user’s data stored at the server. For insertion operation,CSP will insert a new data block and its tag into the server. For deletion operation, CSP will delete the block and its tag from the server. For modification operation, CSP will replace the old block and its tag with the new content. If executed successfully, it will output “success”, otherwise, will output “fail”.

It is important to note that a user needs to perform Step 1-Step 5 again after accomplishing Step 5-Step 8, and questions if the index number of updated block is included in index collection to ensure that CSP can honestly perform the update.

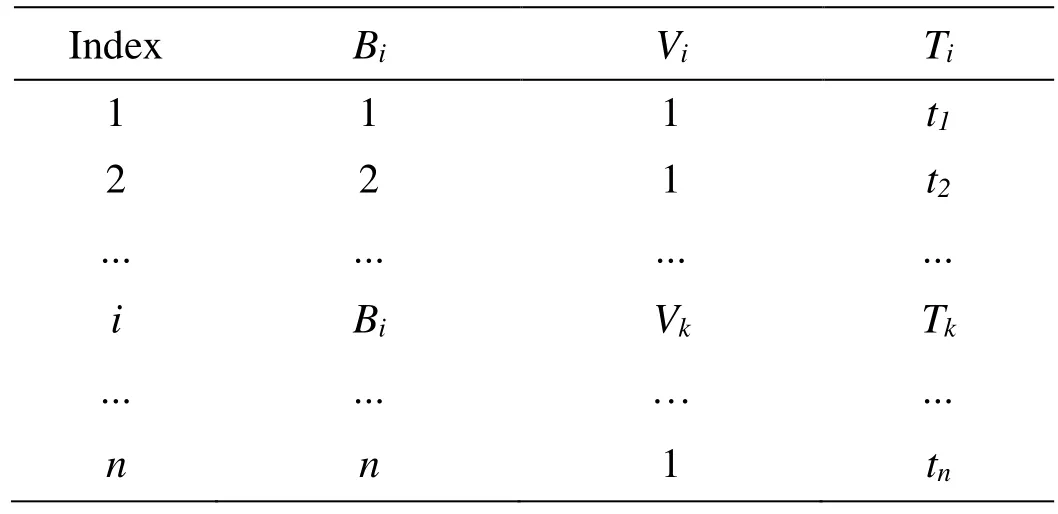
Table 2: The new ITT after modification

In addition, our scheme can also support batch auditing, the execution process for batch auditing is similar to that described above, so we will not repeat it.

4 Security analysis

In this section, we analyze the security of our scheme in detail, including audit correctness, privacy protection, unforgeability, replaying-resistance and substitutionresistance attack.

(1) Audit Correctness: in data audit mechanism, evidences generated by CSP can be verified for integrity only when the user’s data stored at the server is complete, namely,the Eq. (3) is satisfied. Otherwise it indicates that user’s personal data may be damaged.The proof process is as follows:

(2) Privacy Protection: TPA cannot obtain the real content of user’s data during the process of auditing according to the evidence {k, μ, T, π}. This can be proved from two aspects:

On the one hand, according to the formula (2), if TPA wants to get μ’ from μ, it must know the value of r. However, r is randomly generated by the cloud server, TPA cannot be able to get r from CSP. Meanwhile, it can be seen from formula (2) that solving r from k and y is a difficult problem because it belongs to the discrete logarithm. Therefore, TPA cannot infer the value of μ’ from r.

On the other hand, according to the formula (2), we can also obtain that:

Similarly, solvingμ’ from T and k is also a discrete logarithm problem. Therefore, TPA cannot acquire user’s secret information from evidence P it holds.

(3) Unforgeability: CSP cannot use existing data to forge data blocks and tags to trick TPA into integrity verification.

Assuming that user’s data mkis changed to mk'. If CSP wants to pass integrity verification by TPA, it must forge the corresponding tag σk',. However, CSP does not have the knowledge of user’s private key x and the audit information {Bk, Vk, Tk} which are stored in TPA. According to, solvingby g, y and σkis a discrete logarithm problem, therebyis unavailable to CSP. In the end, CSP cannot construct the tag σk' for mk' to fool TPA.

(4) Anti-replaying attack: when a user performs a block update operation, CSP cannot use expired versions of blocks and tags to deceive TPA. That is to say, the malicious CSP may not update the version of a block and its tag after receiving the user's update request.After that, the integrity verification is executed, CSP continues to use the old version to generate evidence in order to be audited by TPA. According to the Eq. (3), we give the following proof process:

Then, we can obtain:

From the anti-collision characteristics of hash function, we can know that the formula (4)is not valid. So, CSP cannot pass the verification by using old version information.

(5) Anti-substitution attack: CSP cannot use valid data blocks and tags to replace the corrupted or lost data blocks and tags being questioned.

Suppose CSP replaces the mhand σhquestioned with legal mkandto generate evidences so as to fool the TPA, then the new evidence is as follows:

From the Eq. (3), we can get:

Substituting (5) into (6), we can obtain:

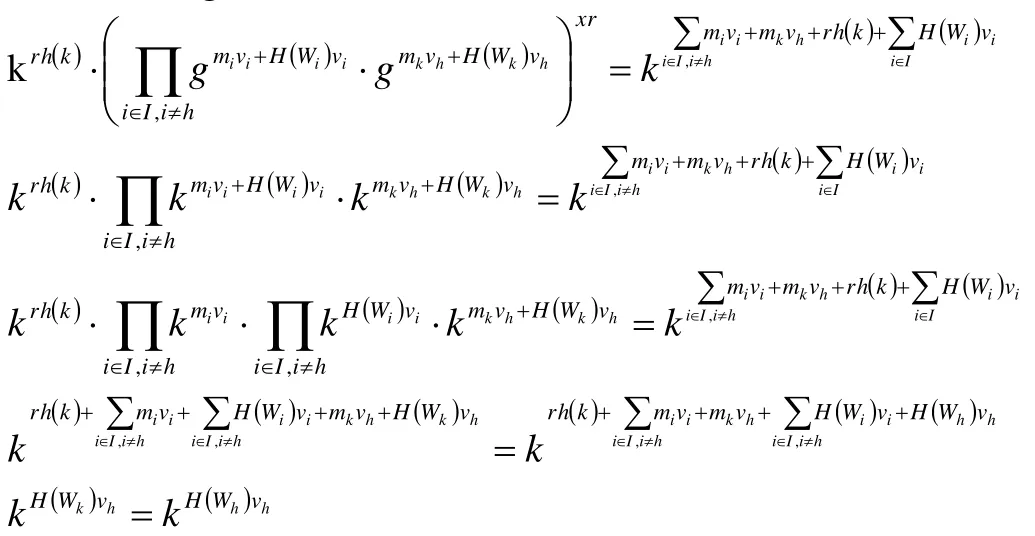
5 Performance evaluation

In this section, we measure the performance of our scheme and make a comparison with silimar method [Cai (2013)]. We developed a prototype on a Ubuntu 16.04 LTS system using C/C++ language. The system is equipped with a 4-Core Intel i5-6500 processor running at 3.20 GHz, 8 GB RAM and a 7200 RPM 1TB drive. Our implementation uses the PBC library at version 0.5.14, OpenSSL library at version 1.0.2n. We choose AES-128 for block encryption and decryption, SHA-1 for hashing, RSA-1024 for verification.

5.1 Function comparison

Tab. 3 lists the functions of our scheme and some common schemes. From Tab. 3, we can see that our scheme can support public auditing, privacy protection and dynamic auditing.PDP [Ateniese, Burns, Curtmola, et al. (2007)] cannot support dynamic auditing and privacy protection, DPDP [Erway, Papamanthou and Tamassia (2009)] cannot support public auditing and privacy protection, MHT [Wang, Wang, Ren et al. (2011)] cannot supports privacy protection and Wu’s scheme [Wu (2017)] is not suitable for dynamic auditing. Although IHT-PA [Zhu, Ahn, Hu et al. (2013)], DHT-PA [Tian, Chen, Chang et al. (2015)] and CDIAS [Cai (2013)] all support three functions at the same time, they all adopt the operation of bilinear pairs which requires a lot of computational cost.

Table 3: The function list for some audit schemes

5.2 Computational overhead

The audit performance is mainly measured from the computational cost of three algorithms: TagGen, ProofGen and ProofVerify. Among them, bilinear operations require much more computing time than other operations. We display the computational overhead of CDIAS and our scheme (seen in Tab. 4).

From Tab. 4 we can see that TagGen algorithm in this paper requires the computational cost of 2nE+nA, which is less than the computational cost of 2nE+nM required by CDIAS, but the computational cost of ProofGen algorithm is slightly greater than that of the CDIAS’s. However, ProofVerify algorithm of our scheme needs only twice exponential operations, while CDIAS’s uses twice bilinear pairings and (c+1) times exponential operations, obviously, the cost of our ProofVerify algorithm is significantly less than that of CDIAS’s.

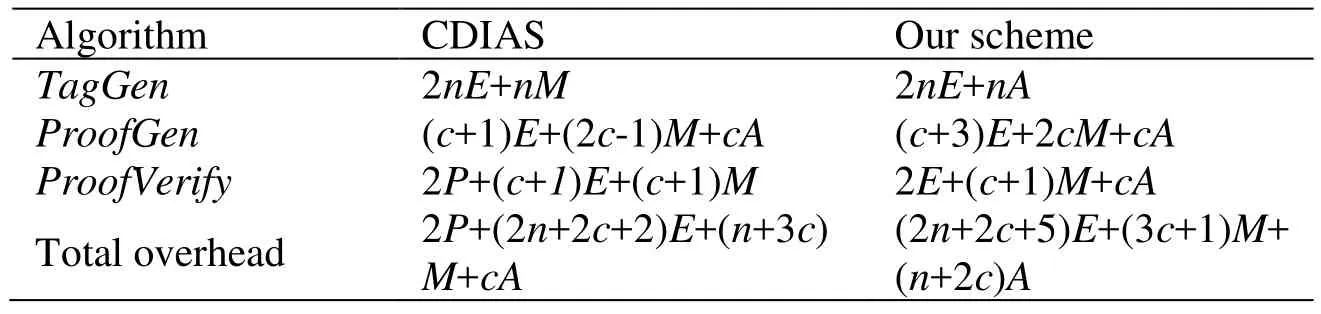
Table 4: Computational overhead for CDIAS and our scheme

5.3 Time overhead

We randomly selected 460 numbers of data blocks to take part in the audit challenge[Ateniese, Burns, Curtmola, et al. (2007)] and tested the time cost of verifying the integrity of a 1 GB file. The size of data blocks ranged from 1 KB to 1 MB, and the experimental results were taken from the average value of 20 trials. The results are shown in Fig. 2 and Fig. 3, including the time of generating tags and evidences, the time of verifying phase and the time of updating operations.

Figure 2: Time overhead of generating tag and evidence, verifying phase

From Fig. 2(a) we can observe that the time taken for TagGen algorithm decreases exponentially with the increase of block size. This is because with the increase of block size, the number of data blocks decreases exponentially, and the number of tags calculated by TagGen algorithm also gets down exponentially. The time of our algorithm only needs about 50% of CDIAS’s. For example, for 1 GB file, when the file is split into many data blocks of 1 KB-size, CDIAS scheme takes 5299.79 s while our scheme takes 2594.77 s, only 48.96% of the former. When the size of data block is 1MB, CDIAS scheme takes 6.38 s while our scheme takes 3.34 s, only 52.35% of the former.

From Fig. 2(b) we can notice that when the size of block is less than or equal to 8 KB, the time taken for ProofGen algorithm decreases as the size of data block increases. When the size of block is greater than or equal to 8 KB, the time taken for ProofGen algorithm is stable for both of CDIAS and ours. Moreover, the time of our scheme is slightly larger than CDIAS’s.

From Fig. 2(c) we can see that with the increase of block size, the time taken for ProofVerify algorithm is stable for both schemes. This is because the ProofVerify algorithm is regardless of the block size. Very clearly, the time of our scheme is far less than CDIAS’s, only 0.17% of the latter.

From Fig. 2(d) we can observe that with the increase of block size, the total amount of time decreases exponentially, and our scheme only needs about 50% of the total computing time of CDIAS’s. For example, for 1 GB file, when the file is split into many data blocks of 1KB-size, CDIAS scheme takes 5307.63 s, while our scheme takes 2600.63 s, only 49% of the former. When the size of data block is 1MB, CDIAS scheme takes 8.77 s, while our scheme takes 4.02 s, only 45.84% of the former.

Figure 3: Time overhead of dynamic update algorithms

From Fig. 3(a) we can see that when the size of block is less than 8 KB, the time it takes to insert 100 data blocks into a file is decreasing with the increase of block size. When the block size is greater than or equal to 8 KB, the consumed time is stable for both schemes. Moreover, the consumed time of our scheme is less than CDIAS’s. For example,for 1 GB file, when the file is split into many data blocks of 2 KB-size, CDIAS takes 1.18s while our scheme takes 0.82 s, which is 30.51% less than the former. When the size of data block is 1MB, CDIAS takes 0.58 s, while our scheme takes 0.27 s, which is 53.45% less than the former.

From Fig. 3(b) we can observe that when the size of block is less than 64 KB, the time it takes to delete 100 data blocks from a file is decreasing with the increase of block size.When the block size is greater than or equal to 64 KB, the consumed time is stable for both schemes, and they are very close in time. For example, for 1 GB file, when the size of data block is 1 KB, CDIAS takes 1.1 s while our scheme takes 1.07 s. When the size of data block is 1 MB, CDIAS takes 17.3 ms while our scheme takes 21 ms.

From Fig. 3(c) we can notice that when the size of data block is less than 8 KB, the time it takes to modify 100 data blocks in a file is decreasing with the increase of block size.When the size of data block is greater than or equal to 8 KB, the consumed time is stable for both schemes. Moreover, the consumed time of our scheme is less than CDIAS’s. For example, for 1 GB file, when the file is split into many 1 KB-size blocks, CDIAS takes 1.59 s while our scheme takes 1.45 s, which is 8.81% less than the former. When the size of data block is 1 MB, CDIAS takes 0.51 s, while our scheme takes 0.28 s, which is 45.1% less than the former.

6 Conclusion

In this paper, we proposed an efficient secure data auditing scheme without bilinear parings based on three-party architecture. It can support dynamic batch auditing as well as privacy protection. We prove its security in detail, including audit correctness,unforgeability, replaying-resistance and substitution-resistance from cloud servers.Compared with similar scheme, it can be concluded that our scheme has higher efficiency and comprehensive function. In the future, we will focus on the following two problems:

1) How to ensure the integrity of user data in situations where users may store data in multiple CSPs to improve reliability.

2) Existing public certification schemes assume that users and CSP are fully trust to TPA,in fact, users and CSP are likely to make collusion with TPA, how to resist collusion attack.

Acknowledgement:This work is supported by the National Key R&D Program of China(2016YFB0800402), partially supported by the National Natural Science Foundation of China under Grant No. 61232004 and the Fundamental Research Funds for the Central Universities (2016YXMS020).