高原滑坡变形与气象因素相关性研究

尹继鑫，何永晴，姚永顺，杨世超，陈兴芳，高桂明

(1.西宁市测绘院，青海 西宁 810001； 2.西宁市气象局，青海 西宁 810003)

1 前 言

西宁是青海省省会，地处青藏高原强震密度较高的河湟谷地，南北两山对峙，整体地势西北高、东南低，平均海拔约 2 261 m，东西狭长，是青藏高原和黄土高原过渡地带，属于大陆性高原半干旱气候，特点是气压低、日照长、雨水少、蒸发量大、太阳辐射强、日夜温差大、无霜期短、冰冻期长。西宁在地质构造上位于祁连山褶皱系中间隆起带南部，地貌类型包括湟水河及其支流南川河、北川河等河谷阶地。该区域地质构造环境复杂，新构造运动活跃，受构造隆升和流水侵蚀作用的影响，在湟水谷地两侧低山丘陵前缘形成了高差300余米，坡度达60°～90°的高陡斜坡。并且由于构成斜坡岩体为第四系黄土与新近系红色碎屑岩，结构松散，强度低，遇水易崩解、软化，加之该区域降水集中，多灾害性暴雨天气，使得地质灾害数量多并集中发育。截至2015年底，西宁市境内地质灾害点 1 206个，其中滑坡420处，崩塌111处，泥石流183处，不稳定斜坡486处，地面塌陷6处，滑坡、不稳定斜坡是西宁市境内最主要的地质灾害，占比高达75.1%。

滑坡是指斜坡上的土体或岩体，受河流冲刷、地下水活动、雨水浸泡、地震及人工切坡等因素影响，在重力作用下，沿着一定的软弱面或者软弱带，整体地或者分散地顺坡向下滑动的自然现象。产生滑坡的基本条件主要有两个方面，从空间来说，斜坡体前有滑动空间，两侧有切割面；从斜坡的物质组成来看，具有松散土层、碎石土、风化壳和半成岩土层的斜坡抗剪强度低，容易产生变形面下滑。

综合滑坡的影响因素，主要包括地质构造、地形地貌、气象条件、人工活动及地壳运动等。本文从气象对地质灾害的影响角度来分析降水、风力、温度、湿度和气压对高原地区滑坡变形的影响。风力、温度、湿度和气压在软化斜坡体、降低坡体强度方面有着重要影响，助推滑坡灾害发育；降水对滑坡的影响最大也最直接，主要表现为，雨水的大量下渗，导致斜坡上的土石层饱和，甚至在斜坡下部的隔水层上积水，从而增加滑体的重量，降低土石层的抗剪强度，导致滑坡灾害产生[1～4]。

2 监测概况

2.1 监测点位布设

为缓解城区交通压力，西宁市规划设计了凤凰山快速路，该路需穿越南山、西山两端山体，其中南山隧道六一桥出口边坡为不稳定滑坡体，为保证隧道贯通工程和周边人群生命财产安全，对南山西坡进行滑坡体变形监测。根据该区域滑坡变形特点、主滑方向，共布设3条观测断面，总体呈5横3纵网络分布格局，共布置各类监测点20个，其中12个点设在抗滑桩顶上，第一排抗滑桩设置4个，第二排抗滑桩设置8个，其他8个点中，7个分两排设置在抗滑桩上部，另外1个放置在第一排抗滑桩一侧，如图1所示。

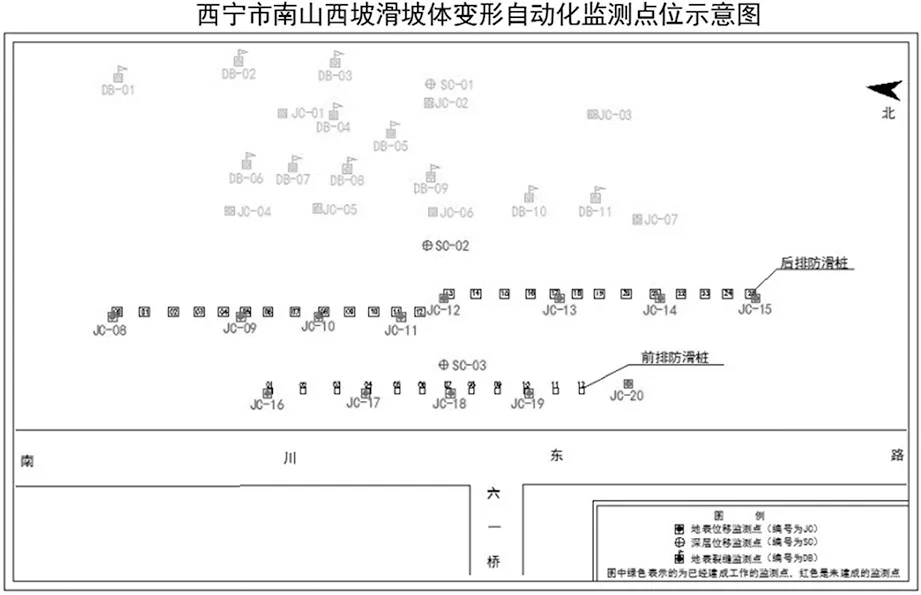
图1 点位布设示意图

图1为南山西坡滑坡体变形自动化监测点位布设示意图。图中编号JC的点即为地表位移监测点。

2.2 监测原理

监测系统采用GNSS自动化监测方式对滑坡体表面位移进行实时监测，工作原理为：各GNSS监测点与参考点接收机实时接收GNSS信号(信号频率为1个/秒)，并通过数据通信网络实时发送到控制中心，控制中心服务器GNSS数据处理软件实时差分解算出各监测点三维坐标，数据分析软件获取各监测点实时三维坐标，并与初始坐标进行对比而获得该监测点变化量。同时分析软件根据事先设定的预警值进行报警，监测预警值参照《建筑基坑工程监测技术规范》(GB50497-2009)执行，防滑桩上监测点的预警值按照深基坑桩顶位移预警值执行，预警值为 30 mm，山坡上监测点位移预警值按照二级基坑坡顶预警值执行，预警值为 60 mm，如监测位移量超过预警值的75%，将以短信、现场广播、声光报警灯多种形式预警[5]。

3 资料来源

在统计分析时，为降低监测数据粗差带来的大幅波动影响，同时为突显阶段性气象因素对滑坡变形的影响特点，以每10日为1个计数时间区段进行数据统计分析，样本时间区间为2016年9月～2018年2月，共计51个时间区段。

3.1 地表位移数据

南山西坡滑坡体变形监测系统于2016年9月建成运行，监测类型主要包括地表位移、裂缝、测斜等，本文选取2号～7号监测点地表位移数据进行研究，6个监测点中，JC03、JC07两站位移数据因通信网络升级改造原因出现个别日期数据缺失情况，对此，利用线性内插方法求得T日(即当日)缺测位移数据，并根据前后日期单日位移量和累计位移量数据进行计算验证，修正T日及T+1日相对位移数据。各监测站总体累计量如表1所示。

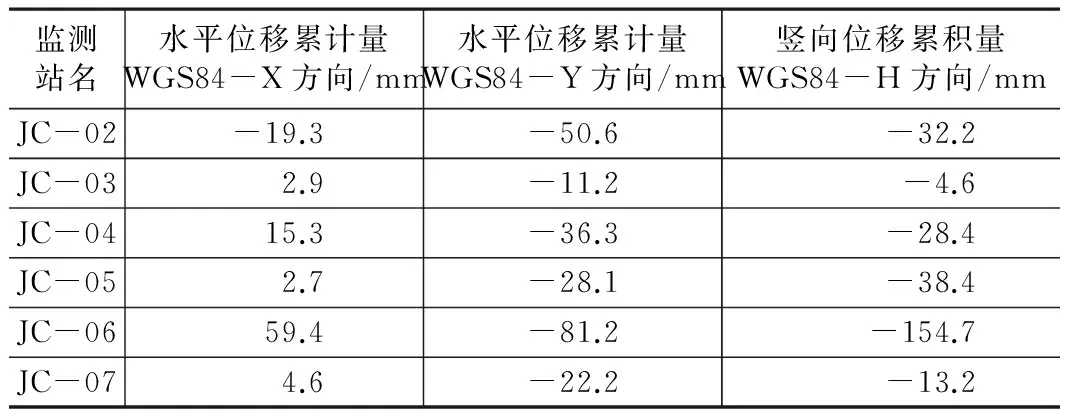
位移累积量统计表 表1

表1为滑坡体变形地表位移累积量统计表。WGS84-X水平方向：正值为向北位移，负值为向南位移；WGS84-Y水平方向：正值为向东位移，负值为向西位移；WGS84-H高程方向：正值为上升，负值为下沉。

根据各监测站水平位移X值和Y值计算出平面位移量(mm)。计算公式如下所示：

(1)

式(1)中：|P|为平面位移量，x1、y1为起点坐标，x2、y2为终点坐标。根据式(1)计算出各站平面位移累计值，如图2所示。

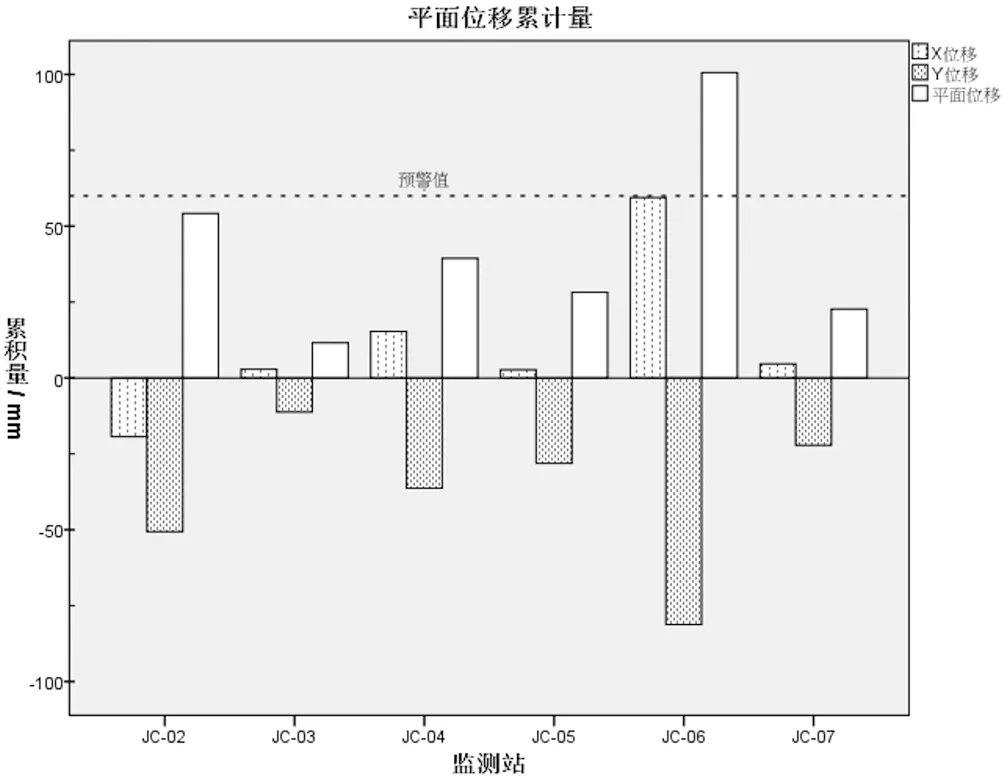
图2 平面位移累计值

图2为平面位移累计值，据图可知JC02和JC06两站平面位移较为明显，在样本时间内，累积量分别约为 54.2 mm和 100.6 mm，平均量分别约为 0.11 mm和 0.19 mm，两站均位于隧道口上方，JC06距离隧道口较近，平面位移已超过预警值，其下沉表现也较为突出。此外，6个监测站主要位移方向均为西向，符合监测区地形特点。

根据总体平面位移和高程方向沉降累计值，绘制出各监测站平面位移和沉降变化趋势图，如图3所示。

图3为位移变化趋势图，上趋势线为平面位移，下趋势线为高程沉降。图中上排从左至右依次为JC02、03、04号监测点，下排从左至右依次为JC05、06、07号监测点。各监测站点个别日期因受通信影响，监测数据出现较大粗差。

从趋势图分析，各监测站平面位移均处于持续增大状态；从趋势线斜率变化而言，JC-06在样本时间后期处于明显上升趋势。

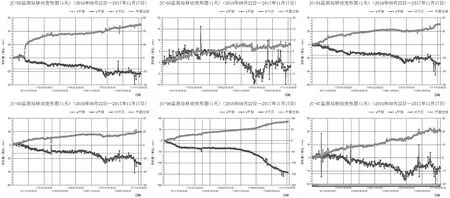
图3 位移变化趋势图

3.2 气象数据

来自西宁市中心城区气象观测站，该站位于北纬36.7°、东经101.7°，测站高度 2 295.2 m，距离滑坡监测区约 1.8 km，主要包括降水量(毫米mm)、最大风速(米/秒m/s)、温度(摄氏度℃)、湿度(百分率%)和气压(帕Pa)等数据，并计算相应的区段平均量和区段累计量等数值，其中将风速转化为风压(N/m2)。风压即垂直于气流方向的平面所受到风的压力，根据伯努利方程推出风压计算公式，如下所示：

(2)

式(2)中：wp为风压，r为空气重度，v为风速，g为重力加速度。

4 相关分析

相关分析用于研究现象之间是否存在某种依存关系，并探讨具体有依存关系现象的相关方向以及相关程度。在进行相关分析、计算监测站平均位移量时，需考虑人工活动对滑坡位移的影响，故应以除JC06站外的其他监测站的平均位移值来修正JC06站数值，修正后数值约为 31.46 mm，以此参与其后计算分析。

4.1 散点分析

为保证相关分析有必要和有意义，可先通过制作散点图来初步观察滑坡位移和降水、风压、温度、湿度、气压等气象因素是否存在相关趋势，如图4所示。

图4为位移-气象散点图，纵轴为滑坡位移量，横轴从左至右依次为降水、风压、温度、湿度和气压，各散点图通过Loess局部加权回归散点平滑法拟合出回归曲线，并推算出相应的线性方程。据图4可知，滑坡位移与降水呈正相关趋势，即降水量越大，滑坡位移量越大；滑坡位移同样受风压、温度、湿度影响，其关系近似对数函数曲线，即受此类气象因素影响至一定程度后不再明显增大，而是接近一个极限值；滑坡位移受气压影响较弱，曲线斜率较小，这与气压在高原地区较平原地区对物体作用较小相符。

图4位移-气象散点图

4.2 偏相关分析

前文4.1中，虽然进行了滑坡位移量与各气象因素的散点分析，但其结果实际仍受其他气象因素影响，而非单一气象因素对滑坡位移量的绝对影响，其相关分析结果如表2所示。因此，为消除其他气象因素对滑坡位移的影响，需利用偏相关分析对数据进行净化研究，同时利用偏相关分析，可剔除对滑坡位移影响相对弱小的气象因子，简化后续分析[6～9]。偏相关分析结果如表3所示。

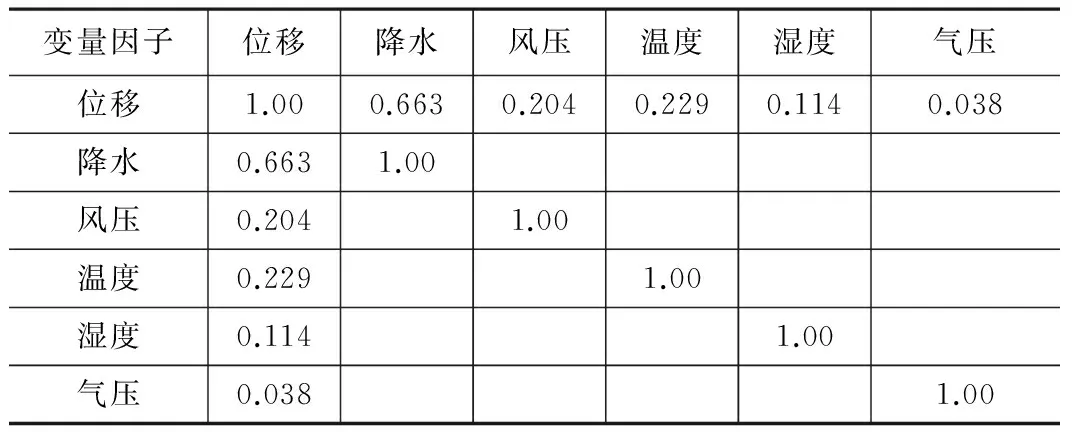
相关分析结果 表2

表2为滑坡位移与气象因素相关分析结果，观察可知，滑坡位移与降水相关性最为密切，其值约为0.663；其次为风压、温度、湿度；气压相关性最小，为0.038。

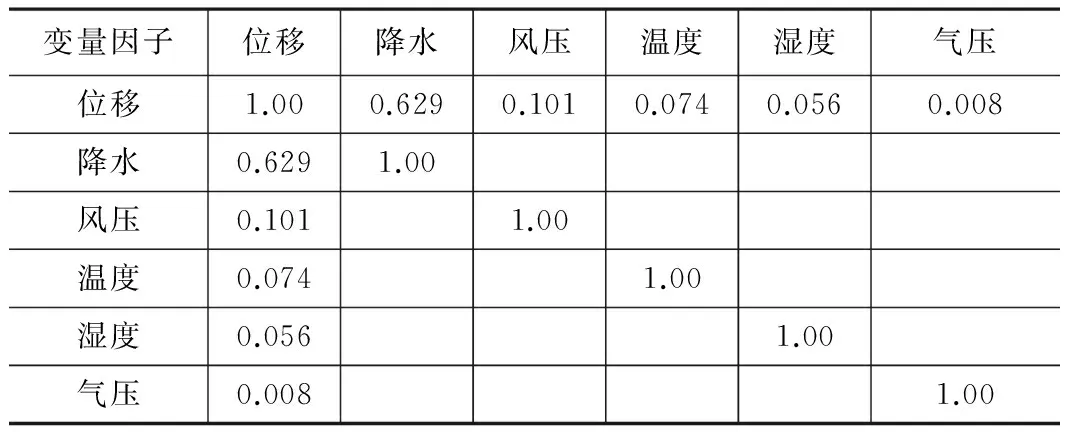
偏相关分析结果 表3

表3为滑坡位移与气象因素偏相关分析结果，在控制了其他气象因素对滑坡位移影响后发现，各气象因子相关系数均有不同程度下降。其中，降水相关系数下降最小，其值约为0.629，对滑坡位移影响仍然最大；风压、温度、湿度、气压相关系数下降较大，下降率均超过50%，气压相关系数仅为0.008。

通过偏相关分析，暂时剔除相关系数小于0.1的温度、湿度和气压3个气象因素，保留降水和风压来建立与滑坡位移量相关的模型方程，并以此来预测滑坡灾害。

5 滑坡模型

通常，利用回归分析来确定现象和影响因子之间的数学关系，建立回归模型，并根据实测数据来求解模型的各个参数，然后评价回归模型是否能够很好地拟合实测数据[10～12]。

5.1 回归方程

本文所述滑坡位移模型涉及降水和风压两个自变量，故为多元线性回归，模型形式如下：

Y=β0+β1X1+β2X2+ε

(3)

式(3)中：Y为因变量滑坡位移，X1、X2为自变量降水、风压，β0、β1、β2为待解参数，ε为回归方程随机误差，其中ε～N(0，σ2)。经回归分析，其结果如表4所示。

回归分析结果 表4

表4为回归分析结果，包含回归系数估值和模型排除变量P值。据表4可知，常量β0估值为1.018，降水量参数β1估值为0.035，在t检验中，降水量和常数项的显著性P值都为0.000，均有显著意义；风压变量t检验的显著性概率P值远大于0.05，故未引入模型。所以回归分析后的模型方程修正为：

Y=1.018+0.035*X1

(4)

式(4)中：Y为因变量滑坡位移，X1为自变量降水。

5.2 模型假设检验

经过5.1回归分析后，得出降水变量参数估计值，并建立了滑坡位移线性回归模型，同时也满足了式(3)中随机误差ε是正态性的假设。在确定滑坡回归模型过程中，通过建立标准残差直方图的方法检验得出ε属于正态分布，结果如图5所示。

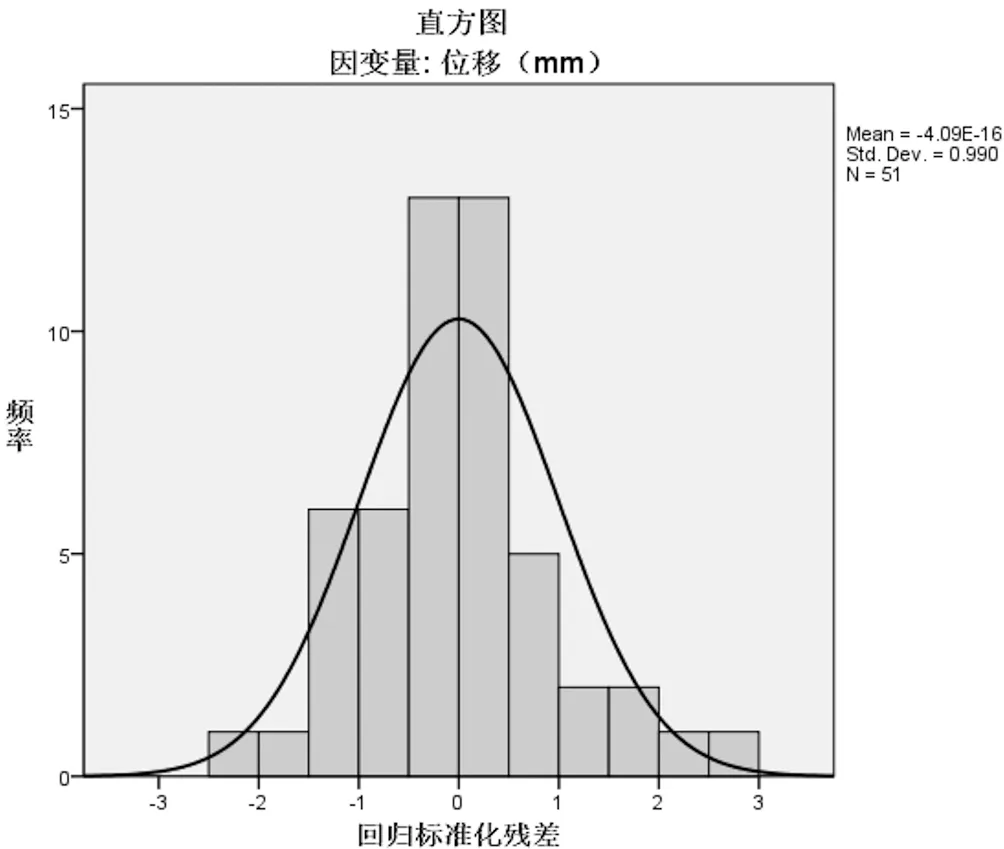
图5 回归残差直方图

图5为回归残差直方图，标准残差服从正态分布N(0，1)，残差正负占比为1∶1，绝大多数落在-2与+2之间，所以满足ε是正态性的假设，因此从一定程度上证明了式(4)中降水量参数和常数项两者的估计值合理，滑坡模型方程有效[13，14]。

6 结 论

影响滑坡灾害的因素是多样的，有内在地质结构作用，也有外在人工、气象影响，而且灾害的发育和产生是通过时间的积累形成的[15]。

(1)通过散点分析得知，高原区域的滑坡位移与降水关系密切，呈正相关趋势；其余气象因素影响相对偏弱，符合高海拔地区气象特点。

(2)通过相关性分析，量化了气象因子与滑坡变形之间的关联程度，分析结果为降水因子与滑坡变形相关程度最高，为0.629。剔除分析结果中相关系数较低的温度、湿度、气压因子来建立回归模型，最终模型为一元线性方程，即Y=1.018+0.035X降水。

(3)建立滑坡多元回归预模型，通过回归分析估算气象因子参数，修正回归方程并检验其合理性。滑坡模型在考虑残差前提下，对气象单一条件下的滑坡位移具有较好的适用性，既可以反映气象因子与滑坡变形的内在联系，又能较好地预测滑坡变形，对于滑坡灾害研究和预测具有重要价值。