盾构隧道贯通前成型管片姿态偏差测量方法研究

吴乃龙，熊开明

(福州市勘测院，福建 福州 350108)

1 引 言

近年来，随着国民经济大力发展，全国城市人口也越来越多，为缓解城市、城际的交通压力，城市轨道交通工程成了解决该问题的重要手段。城市轨道交通工程的线路一般选在最繁华的地段，而与矿山法相比，地下盾构掘进隧道[1]的施工方法具有占用地面道路范围小、路面恢复快等特点，成为目前最常用的地铁隧道掘进工艺。该工艺在施工过程中，成型管片在拼装完后，往往会有如地勘不完善、盾尾注浆后导致上浮或下沉以及为纠偏而拼装错台等情况，导致成型管片拼接后的实际偏差值与盾构机系统内既有参数下所显示的姿态偏差值[2，3]不一致。为此，测量成型管片数据对于线路轴线控制、纠偏、盾构机内的参数调整[4]以及盾构机在贯通时[5]的接收情况有着重要的作用。

本文以福州市轨道交通2号线西洋站至宁化站区间右线为例，在隧道内不同环境条件下，对已拼装成型的管片姿态所采用的测量和偏差计算方法进行了分析研究，并简单介绍了在小半径大偏转角隧道[6]中所使用的控制测量方法。

2 管片姿态测量方法

在盾构机系统中，国内外已有众多学者对于盾构姿态测量进行了研究，较多是利用前方激光标靶、后方棱镜及盾构机上方全站仪，采用前后尺法[7，8]进行测量的方法，从而修正系统参数指导掘进方向，在此不再赘述。

2.1 水平杠尺法

在隧道环境较好的时候，可以采用最简单的水平杠尺测量方法。根据隧道内的条件，定制一副在放水平位置时不受隧道两边管道及走道板影响的杠尺，在杠尺中间贴一张反射片，如图1所示：

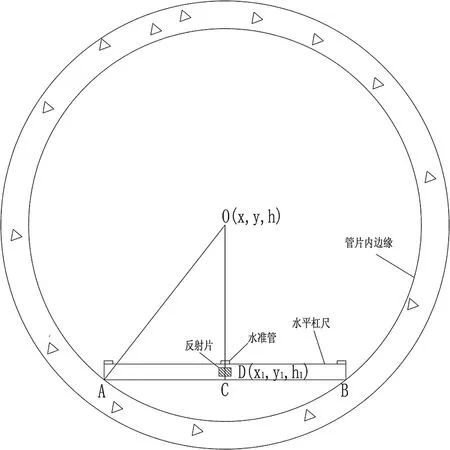
图1 水平杠尺法测量示意图

令其中水平杠尺长度AB=s，反射片中心到杠尺下边缘的高度CD=d1，管片内半径OA=r，反射片中心D到管片中心O的高度为d2，则有：

(1)

假设现场采集反射片中心D的高程为h1，实测管片中心O的高程为h，则h=h1+d2；而反射片中心D的平面坐标即为管片中心O的平面坐标，故采用水平杠尺法所获得的实测管片中心O(x，y，h)三维坐标即为：

(2)

2.2 左右等高法

在盾构掘进过程中，除了隧道两侧的管道和走道板外，往往还有其他影响定制水平杠尺的障碍物，如类似水泥袋子或沙袋的堆载物、接电箱、电瓶车以及盾构机等，如果为了避开障碍物而去制定不同长度的水平杠尺，且每次携带这么多设备，显然不太方便。为此，笔者提出左右等高法，以应对较为复杂的隧道环境。

在设站定向后，以极坐标法[9]采集隧道一侧(肉眼可见的程度不在中线上即可)的三维坐标，按采集到的高程为要求，去采集同一环管片的两侧数据点M和点N，如图2所示。

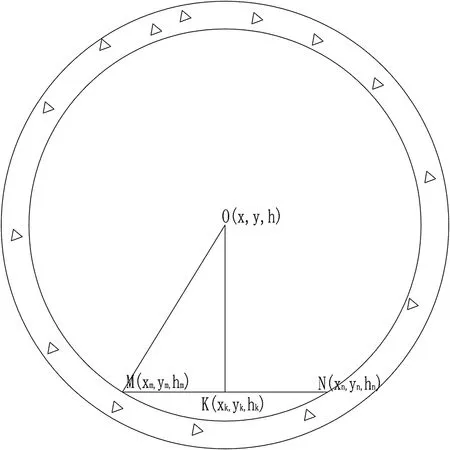
图2 左右等高采集点位示意图

根据弦在立体几何中的性质可知，MN两点中心 K(xk，yk，hk)的三维坐标满足：

(3)

由2.1可知，实测管片中心O的平面坐标与K的平面坐标一致，而其高程h则为：

(4)

其中MN的距离为：

(5)

所以，左右等高法所获得的实测管片中心O(x，y，h)三维坐标即为：

(6)

3 偏差计算

3.1 目标函数

由上述可知，实测中心O(x，y，h)的三维坐标可由实测数据推算得到，现只需求得实测数据所在断面的设计中心O′(x′，y′，h′)的三维坐标，即可获得偏差值，计算式即目标函数如下：

(7)

△h=h-h′

(8)

其中△p为水平偏差值，△h为竖向偏差值。

3.2 设计中心三维坐标推导

在常规轴线计算软件中输入该轴线平曲线和竖曲线参数后，根据现场实测数据所推算的中心O的平面坐标(x，y)可得到对应的里程断面。

当线路轴线为曲线时，会有超高值h超，由轴线设计单位给出，此时线路中心与隧道中心存在不一致的情况，如图3所示：

图3 线路中心与隧道中心关系示意图

上述两中心不一致的量即为偏移量。若线路轴线为直线，则线路中心与隧道中心重合，偏移值为0，可直接由里程得到对应的设计中心坐标和中心高，根据式(7)、式(8)即可就求得偏差。

若线路轴线为曲线，则偏移值不为0，其隧道中心设计坐标是在线路中心的基础上进行偏移而获得。其曲线段中圆曲线段上偏移值计算式如下：

(9)

z竖偏=-h0(1-cosα)

(10)

(11)

其中y平偏为隧道中心对线路中心内侧的水平偏移量；z竖偏为隧道中心竖向偏移量；h0为隧道中心至轨面的垂直距离(如图3所示)；h超为超高值；s滚为滚动间距，一般取 1 500 mm。

而位于曲线段上缓和曲线段上的偏移值，可根据线性内插的方法求得，线路里程与偏移值关系如图4所示，计算式如下：

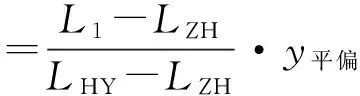
(12)

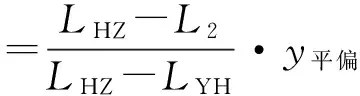
(13)

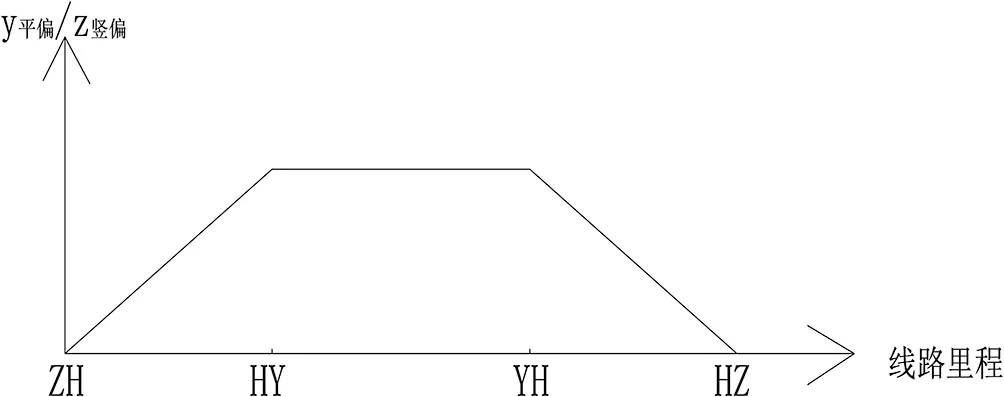
图4 线路里程与偏移值关系图

其中L1为前半段缓和曲线上的里程，L2为后半段缓和曲线上的里程，LZH为直缓点里程，LHY为缓圆点里程，LYH为圆缓点里程，LHZ为缓直点里程。竖向偏移量计算方式与其相同，不再赘述。

从已输入平曲线和竖曲线参数的计算软件中导入里程和偏移值(一般地，轴线偏转角向右，偏移值为正，偏转角向左，偏移值为负)，即可得到隧道中心的三维坐标O(x′，y′，h′)，再根据式(7)、式(8)即可求得偏差。

4 工程实例

福州市轨道交通2号线工程宁化站至西洋站区间右线里程YDK26+497.582～YDK27.681.459，长链 48.177 m，总长度约 1 232.054 m，有3段平面曲线。如图5所示，其中一段曲线半径为 345 m的偏转角为α左=110°36′23.6″，曲线起始直缓点里程ZH YDK26+528.830至缓直点里程HZ YDK27+254.834，长度 726.004 m，隧道全长约58.9%，最大纵坡26‰，为地下单圆盾构区间隧道，覆土厚度 10.7 m～27.1 m，掘进方向为西洋站(大里程)至宁化站(小里程)。

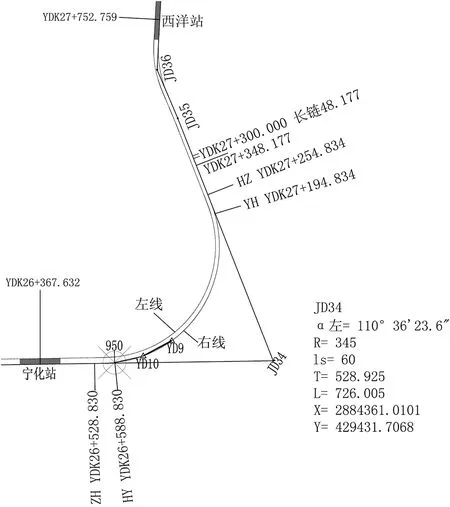
图5 西洋站至宁化站右线最大偏转角平曲线示意图

4.1 地下平面控制网布设

由设计轴线可知，该区间存在小半径大偏转角线路部分，故在平面控制网布设过程中，其可视边长并不长。虽然目前有学者提出如采用三角网、四边形网、虚拟双导线等方法进行布设，但在控制边长不长的情况下，摆设站数越多，测量精度就越差，同时劳动强度也越大。为此，经综合考虑及控制网精度估算[10]，决定采用闭合导线[11]结合陀螺仪[12]测量末端方位角的方法进行施测。

本次隧道盾构掘进至950环(1 140 m)时，已布设10个洞内平面控制点，均为强制对中装置，采用了Leica TS50i高精度全站仪(0.5″，0.6+1 ppm)对地下平高控制网以闭合导线形式进行了按《城市轨道交通工程测量规范》[13]中的精密导线测量要求进行施测，同时在YD9-YD10两点处加测一条陀螺方位边作为已知方位角，经严密平差后，成果符合要求，控制网精度可靠，地下平面控制网精度成果如表1所示。

地下平面控制网精度成果表 表1

4.2 地下高程控制网布设

地下高程控制网是以由地面高程控制网经高程联系测量[14]传递至车站站台层的联系测量两个高程控制点为已知点，在洞内管片上埋设水准点后，采用Trimble Dini03精密水准仪(0.3 mm/km)，按城市轨道交通二等水准测量要求，布设成一条附合水准路线进行施测，地下高程控制网精度成果如表2所示。

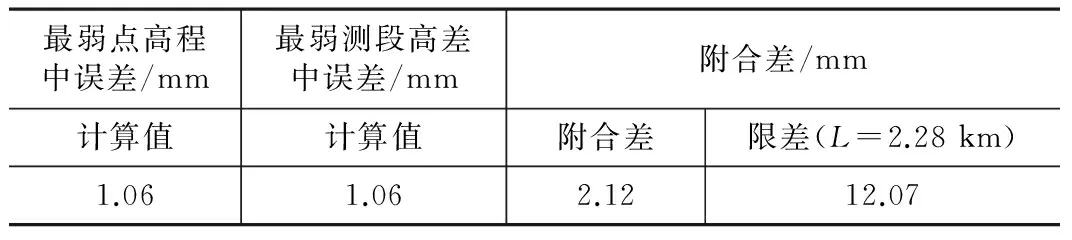
地下高程控制网精度成果表 表2

4.3 管片姿态测量及偏差计算

以已布设的地下平高控制点为起算点，采用全站仪极坐标法进行数据采集，在区间的不同环境条件下，采用水平杠尺法和左右等高法对管片姿态数据进行了测量，每环管片数据均采集到位。部分数据及计算过程如下：

(1)根据设计文件提供的超高值h超=110 mm、隧道中心至轨面的垂直距离h0=1.86 m及滚动间距s滚=1 500 mm，利用式(9)、式(10)、式(11)计算得到水平偏移量y平偏=132.0 mm，竖向偏移量z竖偏=-5.008 mm。

(2)在常规计算软件中输入平曲线和竖曲线参数后，导入已测数据所计算中心的平面坐标得到实测里程及偏离线路中心线的偏距，利用实测里程及式(12)或式(13)可得到对应的偏移量，如表3所示。

(3)根据里程及偏移量即可推算得到对应的设计坐标和设计高，而后通过式(7)、式(8)即可得到`实测管片姿态中心与设计管片姿态中心的水平偏差、竖向偏差及所计算的水平偏差检核值，如表4所示。

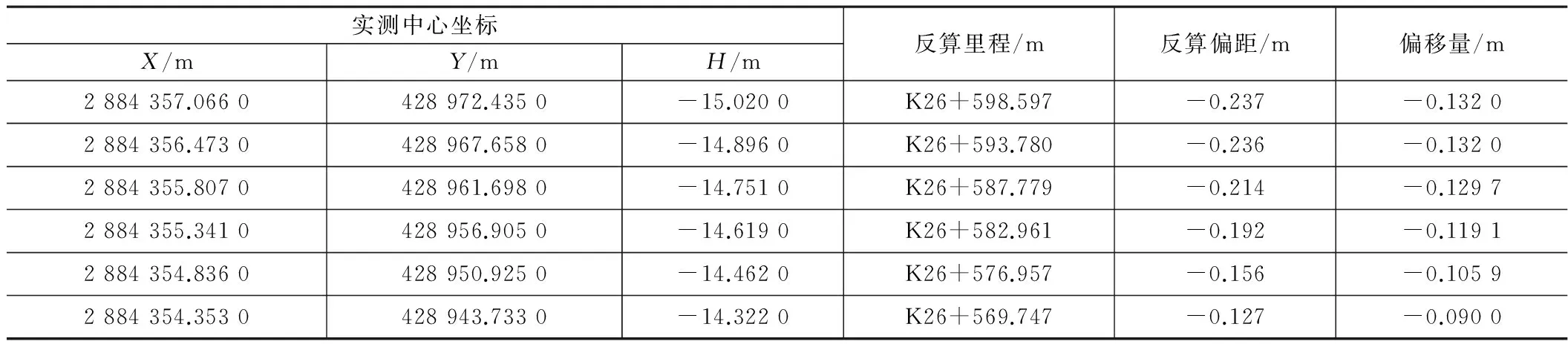
实测坐标推导出的里程、偏距和偏移量 表3

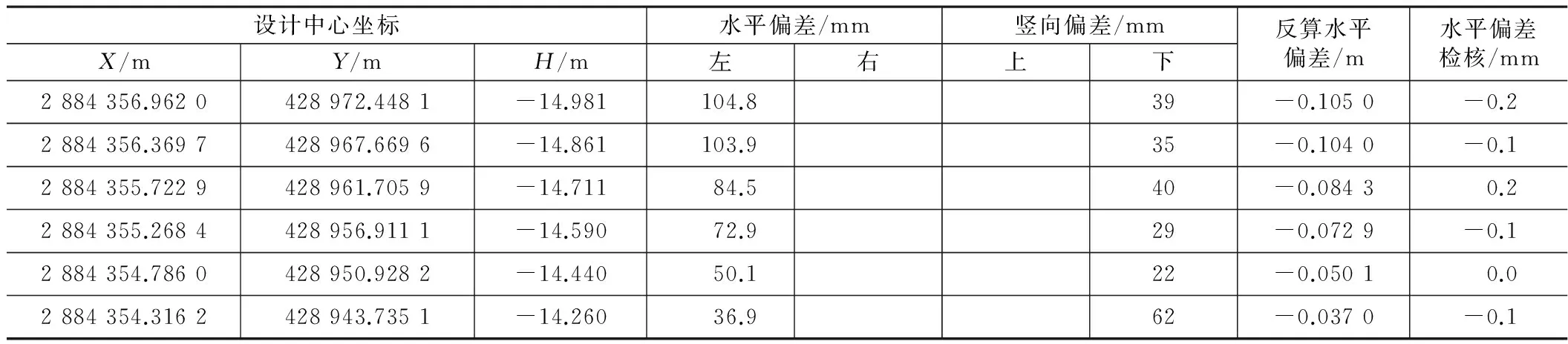
设计中心坐标及偏差值 表4

根据《盾构法隧道施工及验收规范》要求，隧道中心线实测坐标与设计坐标的水平较差和竖向较差的限差为 ±100 mm。由表4可知，里程K26+598.597、K26+593.780所对应的水平偏差已超限，最大为向左 104.8 mm；竖向偏差最大位于里程K26+569.747，为向下 62.0 mm。将上述偏差数据与盾构机内的对应里程的偏差数据进行对比，便可得出成型管片姿态与掘进安装时管片姿态的偏差情况，进而修正盾构机系统内的掘进参数。

5 结 语

通过本文对城市轨道交通工程隧道管片姿态的测量方法和管片中心姿态偏差计算，可应对环境复杂多变的隧道环境，大大减少了因环境影响而无法采集到的数据，降低了工作人员因测量管片而携带不同设备进行作业的困扰，并可根据实测数据计算成型管片姿态的实际偏差，用以指导盾构机系统内的参数修正。

此外，管片安装后的扁率、不规则变形导致的实际半径与设计半径偏差影响，还有待进一步研究。