一种基于泰森多边形的最近服务点搜索方法

魏金占，易桂轩

(1.钦州学院，广西 钦州 535000； 2.武汉市测绘研究院，湖北 武汉 430022)

1 引 言

服务点是指电子地图上的某个地标、景点，用以标示出该地所代表的政府部门、各行各业之商业机构(加油站、百货公司、超市、餐厅、酒店、便利商店、医院等)、旅游景点(公园、公共厕所等)、古迹名胜、交通设施(各式车站、停车场、超速照相机、限速标示)等处所，用于提供服务；兴趣点则是接受服务点所提供服务的地点，可以是某个场所地点或是某用户的当前坐标[1，2]。

最临近服务点的搜索方法是指搜索服务点中离兴趣点最近的一个，一般多采用兴趣点到周边服务点的直线距离逐个搜索，算法各异。常见的算法为根据一定范围搜索兴趣点周边的服务点，之后逐个判定距离大小，最小者即为搜索结果[3，4]。这类方法原理简单，但存在搜索范围过大，效率低下的弊端。此外通过兴趣点找寻服务点，兴趣点的数量一般远大于服务点，如地块到最邻近水源问题，一个县域地块数量多以万计，因此该种模式的搜索从根本上就决定其效率低下。

2 解决思路

传统的最邻近服务点搜索多由兴趣点自身发起，如搜索地块到最邻近水源这类问题，其需要对每个地块逐一搜索。而且一旦服务点如水源发生变化，必须进行重新搜索，算法具有一定的不确定性和效率不高的弊端。

传统的最邻近服务点搜索多以兴趣点作为中心，搜索该点在一定范围内到邻近服务点的距离，选择最小距离为最终结果。对于兴趣点到两个临近服务点的距离判定，可采用两服务点连线，取其中心点垂线作为划分依据，当服务点和兴趣点都在该垂线一侧，由中垂线的定义可知，该兴趣点与最邻近服务点位于垂线同一侧时表明该兴趣点与该服务点较近。而基于中垂线的影响范围确定就是泰森多边形构建的原理，因此本文结合泰森多边形原理和空间分析技术，提出一种新的最邻近服务点搜索算法。该技术首先通过泰森多边形技术构建服务点(区)的服务范围，通过服务点反向查询其服务范围覆盖的区域，如果覆盖区域包含发出请求的兴趣点，则认为该服务区对应的服务点即为该兴趣点的最邻近服务点。该原理与移动蜂窝基站技术类似，将各个服务区服务范围划分为若干子区域，一旦客户进入该区域，即认为兴趣点的最临近服务区就是该服务区。

基于此，本文认为该搜索方法的核心技术在于服务区(点)服务范围的构建及后期的空间分析部分。地理信息技术中泰森多边形是以两点连线的中垂线相交所得多边形范围来确定的，其本质就是基于质心点影响范围的确定。下文将结合实例，阐述该方法具体实现过程及效率对比分析。

3 实施案例

以土地利用分析中地块最临近水源搜索为例，阐述如何利用上述思路实现。众所周知土地利用中对于地块灌溉水源的确认是非常重要的，一般方法多通过地块中心点，搜索周边水源模式来实现[5]。因为地块数量的巨大，搜索参数选取的不确定性，搜索效率不尽人意。根据最临近水源判定标准可知，最近水源面中心点与地块的中心点连线长度是否最小决定其是否满足最临近水源判定标准。基于此，可以认为地块的最近水源意味着该地块在该水源的灌溉范围，因此可以逆向思维，通过水源的灌溉范围和地块中心点的空间关系来确定地块最临近水源。该思路的核心在于水源的覆盖范围确定，因此可做如下考虑：以水源中心点为核心，逐渐外扩构建每个水源点的覆盖范围。该思路与泰森多边形的构建过程一致[6～10]，因此可以借助该原理实现水源灌溉范围的确定，之后通过空间关系确定每个地块最临近水源信息。

本文以超图地理信息系统为实现平台，具体步骤为：

(1)完整性检查，将水源面状数据转换为点状数据并记录对应的属性信息；

①检查水源面状数据属性信息及几何信息的完整性，如图1所示；

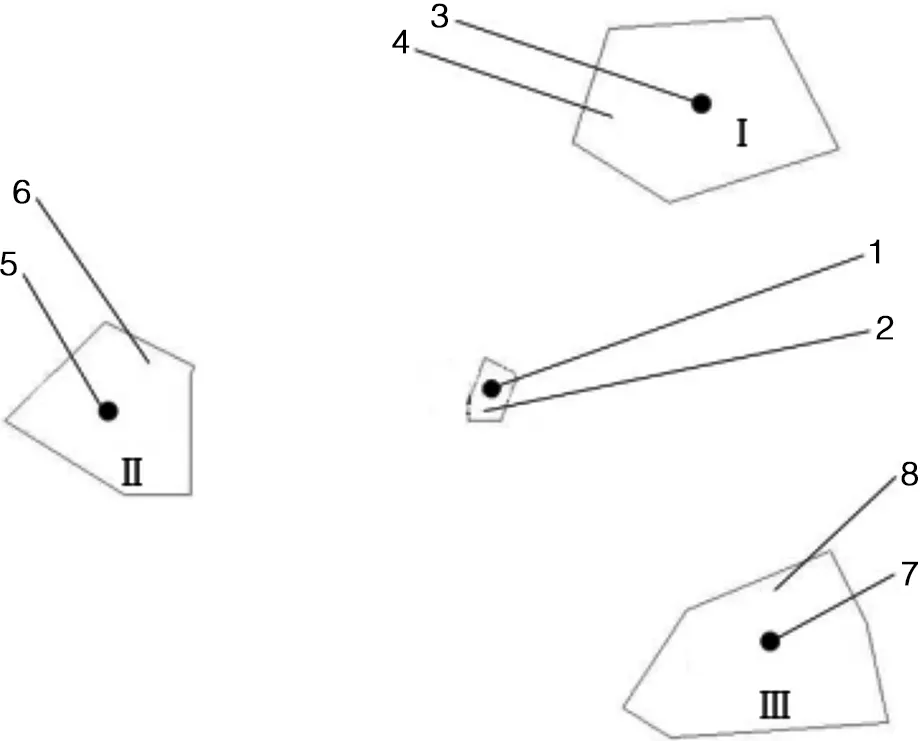
图1 整体区域包括地块1以及水源Ⅰ、Ⅱ、Ⅲ

②将水源范围面状数据进行中心点提取，得到水源点并记录该水源的属性信息；

③将地块范围面状数据转换为地块中心点数据，得到地块点并记录该地块的属性信息；

(2)基于各个水源中心点构建不规则三角网；

将各个水源中心点构建不规则三角网，确定区域内水源覆盖范围，确保每处水源被三角网覆盖，如图2所示；

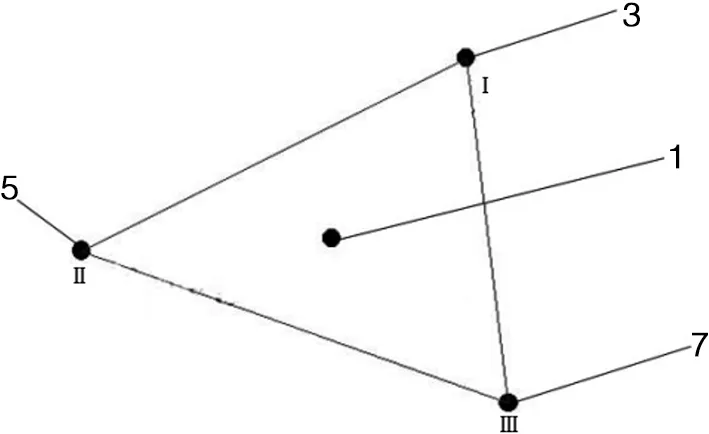
图2 构建的不规则三角网

(3)构建泰森多边形，确定水源覆盖范围

以不规则三角网为准构建泰森多边形，将整体区域划分为多个子区域，各个水源中心点分别位于对应的子区域中，该子区域即为对应水源的服务范围。

(4)求解最邻近水源

通过北京超图地理信息平台将地块中心点与构建泰森多边形后的整体区域进行空间求交，获得地块中心点所在的子区域，则中心点同样位于该子区域的水源即为地块最临近的水源，如图3所示水源Ⅰ、Ⅱ、Ⅲ；地块1位于水源Ⅰ对应的子区域，则地块最临近的水源为水源Ⅰ，求解最临近水源。

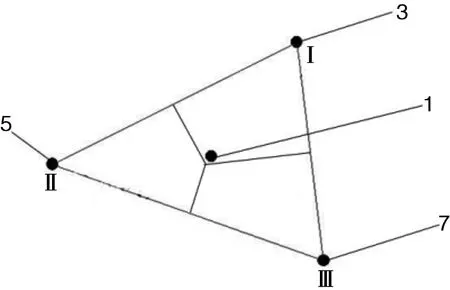
图3 地块1位于水源Ⅰ对应的子区域，则地块最临近的水源为水源Ⅰ

(5)地块变化时最邻近水源求解

将该整体区域的不规则三角网和泰森多边形进行存储，当地块发生变换时，水源覆盖范围不变，因此只需要再次将地块与该泰森多边形进行空间求交即可获得该地块最临近的水源。

如前所述，传统搜索方法必须逐点进行距离或空间判定，按照一个县域10万地块，水源 1 000个计算，运算次数在一亿次以上；而采用该方法，提取中心点、构建泰森多边形、空间分析共计 3 000次运算即可完成，时间节约及效率提升非常明显。以某市二次土地调查图版为例，数据量约10万个图斑，水源数量约0.14万。传统方法耗费超过半小时，新方法仅需要 4 min。而且一旦数据出错，该方法在原有中间数据的基础上几分钟即可完成修正搜索，这是传统方法必须重新计算所不可比拟的。

4 结 语

本文阐述的最临近服务点的搜索方法采用不规则三角网与泰森多边形的结合，简单方便地实现兴趣点周围最临近服务点的搜索。优选用于与位置服务相关的最近搜索，兴趣点可以是如居民区之类，服务点可以是超市、医院等。并且通过服务点覆盖范围模式反向搜索范围内兴趣点的方式，可将第一次搜索构建的泰森多边形作为中间数据存储，当兴趣点发生变动时，仅需将变化的兴趣点与该泰森多边形进行空间求交即可得到所需的最临近服务点，使得搜索一次数据可以多次使用，大大减少了运算量。再者当服务点发生变化时，也仅对该服务点的周边服务点构成影响，只需重新构建新变动服务点附近的泰森多边形，即可完成该泰森多边形的更新，运算量也得到相应减少。

不足之处在于，服务点的服务能力各异，笔者笼统认为其服务能力一致，与实际生产存在差异。再者文中考虑的是重心在对应多边形内的情况，对于不满足条件的情况，需要人工干预。此外该服务区分析基于简单的几何距离，未考虑道路通达性和道路实际距离，因此该方法在宏观服务能力分析方面具有一定的优势同时也存在数据计算偏差的问题，这也是该方法在应用时必须注意的地方。