基于彩色-深度视频和CLDS的手语识别

张淑军 彭 中 王传旭

（青岛科技大学信息科学技术学院，青岛，266061）

引 言

手语是一种重要的人类肢体语言表达方式，包含信息量多，能够表达与语音和书面语等同的语义，也是聋哑人和健听人之间沟通的主要方式。手语识别涉及到视频采集和处理、计算机视觉、人机交互、模式识别和自然语言处理等多个研究领域，是一项具有高难度的挑战性课题。手语识别技术的研究具有深远的理论意义和广泛的应用价值，不仅有助于提高计算机理解人类语言的水平，促进更加智能、友好的人机交互接口的发展，也能够推动失语者在社会各层面的交流、融入，促进社会和谐发展。

对于手语识别的信息获取方法主要有基于传感器和基于计算机视觉两种方法。基于传感器的方法，需要用户穿戴感知设备，设备将姿态及运动数据传送到系统中，再进行处理，该方案对硬件的依赖性过高，使用不便。基于计算机视觉的方案则是从摄像头获取的视频图像中获取信息，借助图像处理技术来识别手语，该方案使用户摆脱了硬件设备的束缚，操作更加灵活，但计算量较大，对算法要求较高。基于视觉的手语识别方法逐渐受到人们的关注。其中基于概率统计模型的方法将隐马尔可夫模型（Hidden Markov model,HMM）模型引入到手势识别领域，并取得了较好的识别效果，而单一的HMM模型不适合应用于数据特征较多的情况，因而限制了手势识别的准确率。另一方面，贝叶斯网络能够根据已知的条件来估算出不确定的知识，已经在手语识别领域有了广泛的应用。Suk等[1]提出一种利用动态贝叶斯网络（Dynamic Bayesian network,DBN）来识别连续视频流中的手语的新方法，提出的基于DBN推理的方法是在皮肤提取、建模和运动跟踪的基础上进行的，在识别静态和连续手势上有较高的准确率。Joshi等[2]利用分布式贝叶斯神经网络对手势进行了准确定位和追踪，识别精度较高。

近些年，基于RGB-D图像的手势识别技术也逐渐发展起来，因为RGB-D信息获取简单方便、信息量丰富且自由度高等特点逐渐受到人们的关注。蔡军等[3]提出了一种基于深度图像信息利用改进的有向无环图支持向量机（Directed acyclic graph support vector machine,DAGSVM）方法进行手势识别。张毅等[4]提出了一种基于深度图像的三维手势轨迹识别方法，该识别方法对视角的变换具有一定的抗干扰性。上述方法都取得了一定的识别效果，但它们都使用静态图像信息，对于连续手语识别在精度和效率上都难以达到预期效果。Wang等[5]提出一种运用矩阵低秩相似的快速手语识别方法，采用方向梯度直方图（Histogram of gradient,HOG）和骨架对（Skeleton pair，SP）对手语进行特征描述，计算出低秩矩阵，构建HMM模型对手语特征进行建模。该方法能取得较好的识别速度和精度，但HMM模型构建困难。Wang等[6]又提出了一个动态手语识别的稀疏观测模型，使用RGB-D信息以及HOG特征描述手势，构建了一个手势关系图来生成不同的低维空间观测特征代替HMM模型，加快了匹配速度，同时结合3D动作轨迹，使系统对多种手势具有鲁棒性。但是该模型只考虑了手与手臂的局部动作，无法识别需要结合身体其他部分共同识别的手语。近年来出现了一些基于深度学习的手语识别工作的研究[7-9]，能够取得较高的准确率，但是深度卷积神经网络算法需要大量数据长时间的训练，且对硬件的依赖较高。

线性动态系统（Linear dynamic system,LDS）是一种常用的时序建模模型，它对特征之间的相似性测量[10-11]使其在高维时间序列数据在动态纹理领域有新的发展。但是在LDS中，转移矩阵不是唯一的，它受到置换、旋转和线性组合的影响，输出矩阵也是如此。因此，LDS存在生成特征序列与原视频不完全对应的情况，导致特征描述符之间的距离计算不够准确，因而影响手语或行为识别精度。文献[12]提出了复线性动态系统（Complex linear dynamic system,CLDS）的概念，并将其与LDS,主成分分析（Principal component analysis，PCA）,离散傅里叶变换（Discrete Fourier transform，DFT）及其他时间序列方法进行了比较，论证了CLDS在聚类时更具有旋转不变性。

本文将CLDS建模方法引入到手语识别领域，使生成的手语特征序列可以与原视频准确对应，保证识别的准确率和鲁棒性；同时，将RGB视频和深度视频分别提取MBH特征后再进行融合，去除数据干扰，深入挖掘视频数据所蕴含的手语行为特征，最终获得了优异的识别精度。

1 LDS时序建模

基于计算机视觉的手语识别本质上是从手语视频中挖掘和提取不同手语动作序列的特征，构建较高层的特征描述符，以得到辨析度较好的分类结果。一个手语动作序列可看作一个时序系统，通过LDS对其进行时序建模，可获得该序列的时序特征。LDS可以由系统转移矩阵和子空间映射矩阵共同组成的参数元组M=(A,C)表示为

式中：A∈Rn×n为系统的转移矩阵，n为状态空间的维数；C∈Rn×n为子空间的映射矩阵；xt∈Rn为状态变量或称为潜变量；yt∈Rp为观测的随机变量或特征，p为观测空间的维数；vt和wt分别为系统噪声和观测噪声。假设系统噪声和观测噪声是均值为0的高斯过程，则可以得到vt～N(0,Q)以及wt～N(0,R)。这里的Q和R是协方差矩阵且满足多元高斯分布。

在式（1）中，隐藏状态被建模为一阶高斯马尔可夫过程，其中xt+1由先前的状态xt确定。输出yt取决于当前状态。给定视频序列并学习其内在动态信息等同于识别模型参数M。这通常是典型的系统识别问题，通过使用最小二乘估计来解决。

假设给定列矩阵 Y1：τ=[y1,y2,…,yτ]和 X1：τ=[ ]x1,x2,…,xτ分别表示观察序列和状态序列，为了得到参数元组M的准确估计，需要对观察矩阵进行奇异值分解Y1：τ=UΣVT。其中U和V是正交的，Σ是正对角线上没有负值的实数对角矩阵。基础状态序列和子空间映射矩阵的估计值为

然后通过保留超过给定阈值的奇异值来确定模型维数n的值。则A的最小二乘估计为

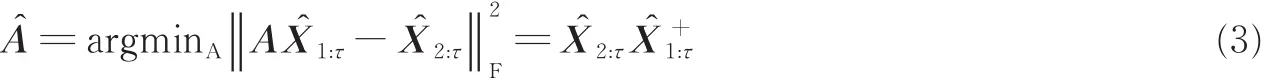
式中：“‖‖F”表示F范数，“+”表示Moore-Penrose逆矩阵。给定上述Aˆ和Cˆ的估计，可以直接从残差中估计协方差矩阵Qˆ和Rˆ。

根据式(2)可知，LDS运用子空间映射矩阵C和其对应的系数X1：τ来隐含的观测序列Y1：τ。在手势识别中，子空间矩阵C用来描述动作分量，矩阵A从X1：τ导出并表示运动状态。因此可以用M=(A,C)来表示运动序列描述符。

但是，使用M作为描述符存在问题。LDS方法通过将动作序列解耦成子空间姿态和潜在的运动状态来跟随时间变化，但由于转移矩阵A与输出的子空间映射矩阵C受到排列、旋转和线性组合的限制，输出矩阵中的每一行都不能唯一地表示相应系统的特性。本文使用的时序模型是基于线性动态系统的改进，通过将其扩展到复数域，依据复线性高斯分布的性质改进的模型称为CLDS模型，CLDS模型可以提取时间序列的不变特征。

2 基于RGB-D视频和CLDS的手语识别

本文提出一种基于RGB-D视频和CLDS的手语识别方法，如图1所示。首先，输入彩色视频和深度视频，分别提取相应的运动边界直方图（Motion boundary histograms，MBH）特征。将得到的两组特征序列进行融合，作为CLDS建模的输入变量。通过CLDS时序建模，用特征描述符M=(A,C)对原始视频进行描述。计算多个特征序列M之间的距离，生成子空间角度的距离矩阵；最后将距离矩阵送入改进的KNN分类器中，输出分类结果。

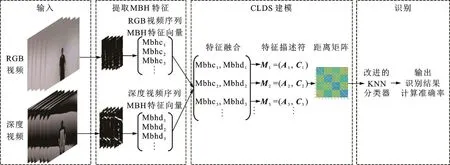
图1 本文方法框架图Fig.1 Framework of proposed method

2.1 MBH特征提取

MBH专门描述运动物体的边界，实质上就是图像在x和y方向上光流图像的HOG。将MBH特征用于手语识别，对输入的每个彩色视频和深度视频计算光流图，然后分别沿光流图的x，y方向提取HOG特征，构建运动边界直方图MBH，得到手语识别的底层特征。MBH特征非常适合于在动态背景下通过运动来进行人体检测。

MBH专门描述运动物体的边界，实质上就是图像在x和y方向上光流图像的HOG。将MBH特征用于手语识别，对输入的每个彩色视频和深度视频计算光流图，然后分别沿光流图的x,y方向提取HOG特征，构建运动边界直方图MBH，得到手语识别的底层特征。MBH特征非常适合于在动态背景下通过运动来进行人体检测。

MBH特征的计算方法如下：

（1）对于运动边界描述，通过求解静态图像标准HOG描述符来捕获运动边缘的局部方向。

（2）将水平和垂直的光流分量Lx,Ly视为独立的图像，分别取其局部梯度，找到相应的梯度幅度和方位。

（3）将这些作为加权进行投票用于局部方向直方图，方法与求解标准HOG一致。

MBH可以为每个光流分量建立单独的直方图，或者可以组合两个通道。通过实验发现单独方向的直方图更具有判别力。与标准HOG一样，在没有任何形式平滑的情况下以尽可能最小的比例[1,0,-1]来获取空间导数的效果最佳。MBH描述符如图2所示。

图2 MBH描述符Fig.2 MBH descriptor

图2(a，b)是时间t和t+1的参考图像。图2(c，d)为计算的光流量和显示运动边界的流量大小。图2(e，f)图像表示图2(a，b)所产生的光流场Lx，Ly的梯度大小。其中符号Lx,Ly表示包含光流的水平和垂直分量的图像。图2(g，h)反映了光流场Lx,Ly的所有训练图像上的平均MBH描述符。MBH特征对提取人体轮廓的效果显著，计算简单易用，很适合运用在手语识别方面。

2.2 CLDS建模

以往的LDS可能会出现生成数据与原始数据不对应的情况。CLDS噪声变量遵循复高斯分布，复高斯分布的一个重要特性是“旋转不变性”。因此，可以用它来获得相应序列的不变特征，该特征对于分类至关重要。复线性动态系统模型为

式中：噪声向量满足复高斯正态分布w1～CN(0,Q0),wi～CN(0,Q0),vj～CN(0,R)。这里满足的分布与LDS不同，LDS中的分布均为实数范围，而CLDS的分布允许参数为复数值，约束为Q0，Q和R必须是Hermitian正定矩阵。图3描述了CLDS的图模型，它可以看作是隐藏变量z和观测值x的连续线性高斯分布，x是实值观测值，z是复数隐藏变量,箭头表示线性高斯分布。

为了解决如何学习得到最好的拟合参数集θ={u0,Q0,A,Q,C,R}问题，引入一种带复值的最大期望算法——Complex-Fit算法用于最大似然估计。CLDS的预期负对数极大似然估计为

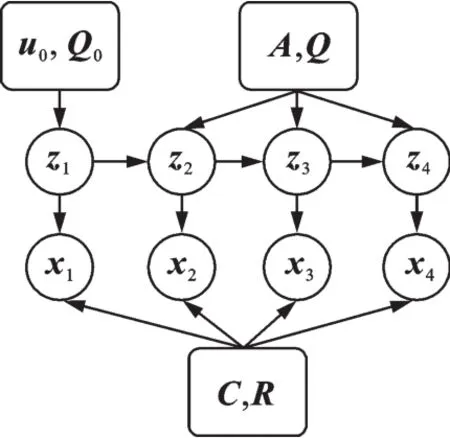
图3 CLDS的图模型Fig.3 CLDS model

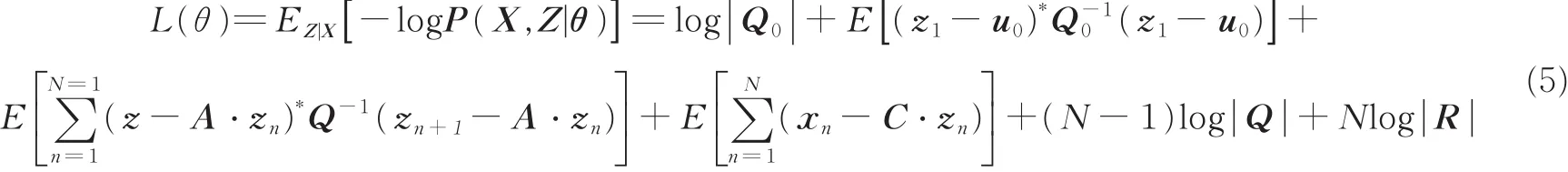
式中，期望E[]是X对Z的后验分布的期望。

与LDS不同，这里的对象是复数值，需要在复数域中进行非标准优化。在负对数极大似然估计中，存在两组未知数，参数集和后验分布的值。Complex-Fit算法的实现分为M-step和E-step两步，M-step是通过求得目标函数L(θ)偏导数并令其等于零，最终得到使用隐变量z和观测值x表示的参数集表达式，M-step中需要得到隐变量z的统计分布才可以充分表达参数集θ在E-step中，可以计算出边缘后验分布P(zn|X)和后验分布P(zn,zn+1|X)均值与协方差。在E-step中运用前后子步骤（对应LDS中的卡尔曼滤波和平滑）来计算后验分布，前子步骤用来计算部分后验分布zn|x1…xn表达式，后子步骤可以得到最终的后验分布。Complex-Fit算法的总体思路就是优化参数集设定初始参数集，计算得到后验分布的结果后更新初始参数集，再用当前参数估计后验分布，然后循环迭代获得最佳的优化方案。

使用Complex-Fit（使用对角线变换矩阵）来准确地估计这些参数，使得CLDS中的输出矩阵M=(A,C)作为表示运动序列描述符的特征，并计算这些参数之间的距离，最后使用分类器进行分类。

相对LDS而言，CLDS可以较好地解决数据不对应的问题。主要原因有两方面：（1）在LDS中，转移矩阵和输出矩阵都会受到原始输入数据置换、旋转和线性组合的影响，生成的特征序列与原视频不能完全对应，而CLDS模型将转移矩阵A用对角转换矩阵表示，且通过复数值来准确描述隐藏变量，相当于寻找最优解。（2）LDS模型没有对时移问题做出明确的解释，而CLDS模型通过设定初始状态和输出矩阵C对时移问题进行编码。

2.3 CLDS的距离矩阵

对于给定运动的序列，现已得到CLDS模型所输出参数M=(A,C)作为其描述符，其中动态矩阵A∈GL(n)，GL(n)是所有大小为n×n逆矩阵组，以及映射矩阵C∈ ST(p,n)，这里的ST(p,n)是Stiefel流型。由于模型空间具有非欧几里德结构并且描述符是非矢量形式，如何测量两个描述符之间的相似性就是一个关键问题。文献[13]基于其倒谱系数的比较后定义了稳定自回归滑动平均模型（Autoregres⁃sive moving average model，ARMA）模型的度量，文献[14]通过使用两个LDS之间的子空间角度来改进Martin的工作。因此，这里定义子空间角度为无限可观测矩阵的列空间之间的主角度

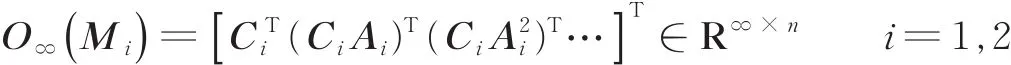
令M1=(A1,C1),M2=(A2,C2)为两个运动序列的描述符，子空间角度的计算结果通过求解Ly⁃apunov方程来得到

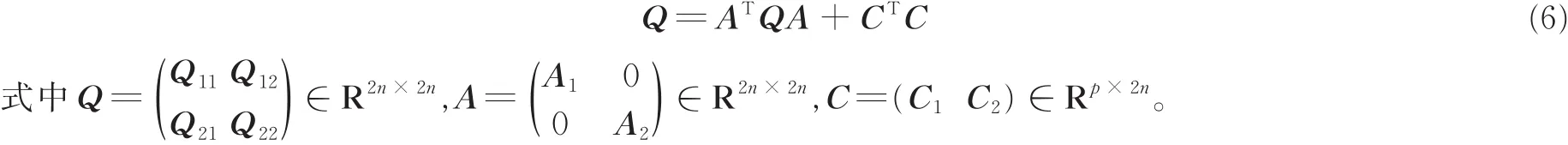
式(6)在保证M1,M2为固定值时才存在，子空间角度的余弦cos2θi作为特征矩阵Q-111Q12Q-122Q21的特征值，其中Qkl=O∞(Mk)TO∞(Ml),k,l=1,2定义子空间角度的距离为

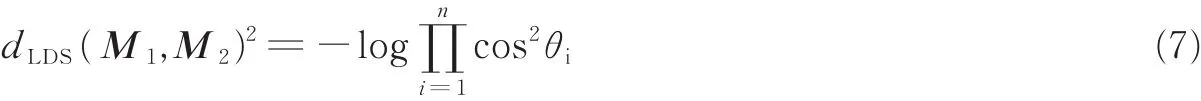
根据式（7）即可判定两个运动序列M1和M2的相似性。有了相似性计算准则，再使用改进的KNN算法即可进行最终分类。由于传统的K最近邻（K-nearest neighbors，KNN）算法容易受噪声的影响，尤其是孤立的噪声点对分类会产生很大影响，因此，本文采用一种改进的KNN算法[15]，根据距离的远近进行加权投票，从而去除干扰项，得到更为稳定可靠的分类结果。根据式（7），采用距离平方的倒数作为加权值进行加权投票，通过选取合适的K值，对CLDS得到的特征矩阵进行准确分类。

3 实验结果与分析

使用中国科学技术大学建立的中国手语（Chinese sign language,CSL）数据集[16]对所提出的方法进行实验验证。此数据集中包含500个手语实词，词汇范围主要涉及日常用语和教学用语。每种手语有50人各打5次的视频数据。每个视频的时长约为2～4 s，手语视频样本的平均帧数为80帧左右。深度视频和彩色视频相对应。该数据集涉及的手语实词满足了日常生活的正常交流用语。选取彩色和深度视频中的不同帧如图4所示。实验硬件平台和软件环境为：操作系统Ubuntu 14.04，服务器处理器Intel(R)Xeon(R)CPU E5-2620 v4（主频2.1 GHz），软件平台 Matlab2016b。

图4 中国手语数据集的部分图像Fig.4 Some frames from CSL Data Set

3.1 MBH特征提取结果

首先对RGB视频和深度视频分别提取连续的MBH特征。分别计算x，y光流分量的梯度来编码像素之间的相对运动,其提取的特征可以明显地突出运动的前景主体。将视频帧大小调整为64像素×128像素,通过用8像素×8像素单元的2×2块将方向量化为9个单元来计算MBH。为了提高性能，块重叠（0.5）也被纳入,因此，可以总共获得7×15个块，其中每个块由4×9个直方图描述。对于MBH在光流x和y方向上的分量（7×15×36），最终的直方图大小是3 780。部分手语动作帧图像及提取的MBH图如图5所示。

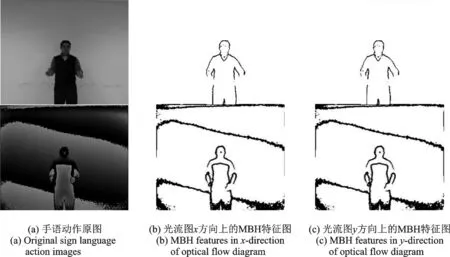
图5 手语动作的原图和MBH(x,y)图Fig 5 Illustration of raw and MBH(x,y)images

3.2 最终识别结果及对比分析

将提取的MBH特征进行特征融合，由CLDS建模得到子空间距离矩阵，将距离矩阵送入KNN分类器得到最终的分类结果。采用留一法在CSL数据集上进行实验测试来获得每次实验的准确率。实验选取500类手语实词中的300类进行实验，从第1～300类每100类进行一次识别验证，将3次结果进行汇总，取平均识别率作为最终的分类准确率。

选取400～499类的分类结果作出图6。从图6可以看出视频的分类准确率达到99%以上，大部分视频分类准确率可达到百分之百。

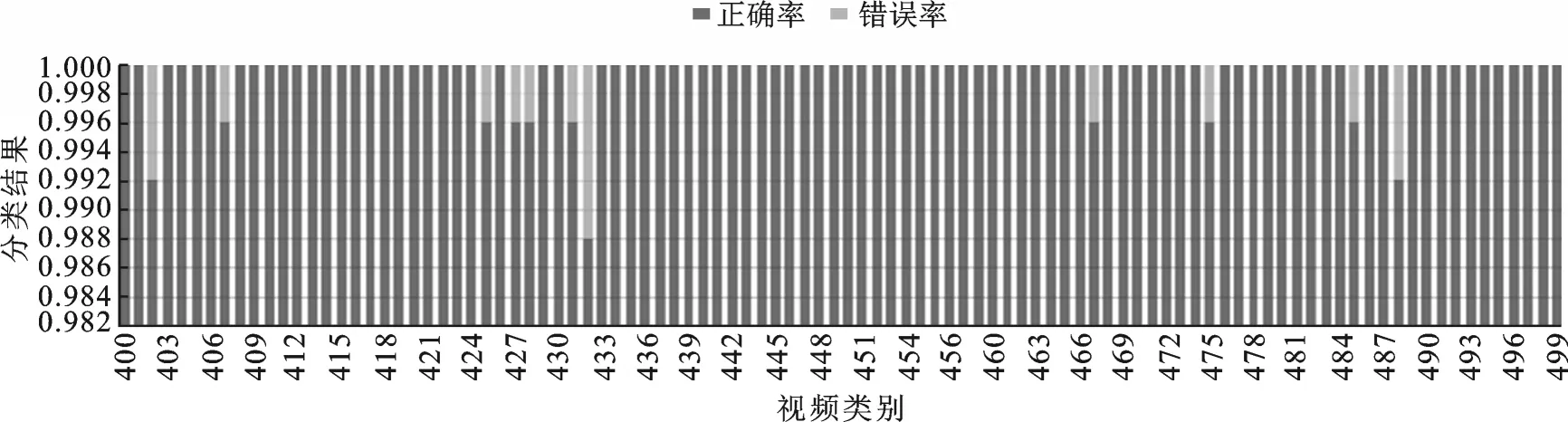
图6 视频分类结果Fig.6 Result of videos classification

在实现手语识别等任务时，通常有两种整合空间和时间信息的策略：（1）提取同时具有时空特征的高层描述符来描述手语视频，并基于这些特征构建分类器进行识别；（2）只提取图像的底层空间特征，利用隐马尔可夫模型等时间序列对特征进行时间轴上的建模。本文使用的CLDS有出色的时间序列构建能力，为进行对比分析，选取了4种当前的代表性工作在CSL数据集上进行实验，分别是：时空兴趣点（Spatio-temporal interest points,STIPs）、改进的密集轨迹（Improved dense trajectories,iDTs）、高斯混合隐马尔可夫模型（Gaussian mixture model-hidden Markov model,GMM-HMM）以及加入注意力机制的3D卷积神经网络（3D-convolutional neural networks，3D-CNN）。

STIPs是常用的时空特征，iDTs也是目前比较好的人工标注特征,3D-CNN是目前提取时空特征可用的新方法。STIPs是通过检测视频中的3D Harris角并计算检测点周围的HOG和HOF特征组成。基于光流跟踪和低水平梯度直方图的iDTs则由轨迹，HOG，HOF和MBH特征组成。从视频中提取出STIPs和iDTs特征后采用Dft_fisher工具箱将这些特征编码为Fisher Vector[17]，最后对编码后的特征使用SVM进行分类。引入注意力机制的3D-CNN在提取特征后运用Atten-pooling方法[7]进行分类。而GMM-HMM是时序模式识别中的传统方法，可以较好地构建手语视频中的时序特征，并进行分类。将上述4类模型与本文提出的基于彩色深度视频和CLDS的识别方法进行比较，得到的结果如表1所示。

表1 不同方法的平均准确率Tab.1 Average accuracy of different methods

表1列出了不同模型的平均识别率，比较发现本文方法的识别率要比手动的特征分类方法准确率高，比传统的GMM-HMM手语识别模型的识别准确率要高出40%以上。从第200～499类每100类的平均识别准确率分别为0.997 24，0.994 19，0.999 40，对应标准差为0.002 137 293，识别准确率稳定，波动小。实验结果表明本文方法对手语特征提取的时序信息更为有效，识别精度更高。在算法效率方面，实验中平均每100类视频的识别时间为0.554 s，单个视频的识别时间为0.053 s左右。相对深度学习方法，本文算法无需依赖高性能的GPU对整个数据集进行前期训练，处理比较灵活；在数学逻辑和时序分析上更加清晰和严谨，对数据的处理过程都有严格的数学逻辑推理。

4 结束语

手语识别是目前计算机领域研究的热点之一，本文提出了一种基于RGB-D视频和CLDS的手语识别方法，通过将彩色视频与深度视频相融合，使用MBH方法，得到特征描述能力更丰富、准确的底层特征。利用复线性动态系统对视频序列进行时序建模，学习其内在的状态并估计出最优参数，输出参数元组M=(A,C)来唯一表示每个手语序列。利用线性动态系统的子空间角度来计算不同线性动态系统的距离。最后利用改进的KNN分类方法进行分类。经实验验证，本文方法可以获得非常高的准确率，且具有良好的鲁棒性和抗干扰能力。该方法也可用于信号压缩等领域中，下一步也将考虑开发一种非线性动态系统模型并用于手语识别或其他行为识别中。