基于三支决策的序列数据代价敏感分类算法

刘牧雷，徐菲菲

（上海电力学院 计算机科学与技术学院，上海 200090）

当前，LSTM 作为深度学习的一种处理序列数据最为流行的解决方案，拥有着较传统方案更加实用性强且准确率高的特点[1-2]。但是，基于深度学习的代价敏感决策仍未得到主流的研究关注。当前的研究重点多集中于如何更高效的获得精确的整体准确率。在有关于深度学习的代价敏感分类或决策问题上，当前的算法常见解决方案多集中于通过对数据的预处理和运行参数调整的方式来使分类器获得对某一类代价敏感类别更高的关注从而实现减少整体的代价[3]。但是这种方法的缺点如前文所述。为了训练对高代价分类敏感的模型，筛选出的数据集将会面临严重的数据不平衡问题。而无论是填充或者再平衡的方式，都会使原数据集的结构改变[4]。其次，无论是对数据集的预处理还是对运行参数或者模型结构的调整，都与具体问题相关性较大[5-7]。对于不同的具体问题，数据清洗和参数调整或模型调整的优劣与模型设计者的经验与对问题的了解有着较大的关系。并且，对于不同的问题，相同的解决方案并不能保证稳定的表现。在不同的数据集之间，相同的数据清洗和参数调整所带来的模型上的改变影响是不同的。

基于此，本文提出的将三支决策运用于深度学习模型能够一定程度上解决上述问题。1) 三支决策算法的理论基础为粗糙集理论，以分类置信度为基础判断决策或分类代价。从算法逻辑的角度，三支决策算法要求更高的全局分类的准确性而不是对单独高代价类的分类，此特点使得三支决策算法与更高的更广泛的分类算法优点相结合，在前置分类器不用做出改动或者调整的情况下降低决策的风险。2) 三支决策算法倾向于判断单独决策。因此，新改进的算法将避免在正常预处理的前提下，将避免因平衡特殊分类类别而造成的数据重新扩展或裁剪，从而进一步影响数据平衡问题。综上，结合三支决策的LSTM 模型可以在原先的深度模型的基础上，进一步增强模型在代价敏感问题上的表现。

1 相关工作

1.1 三支决策

三支决策[8]是Y.Y.Yao 由概率粗糙集理论提出的一种新决策思想。相较于传统的“是，否”二支决策而言，三支决策提出了一种不同但是更合理的决策思想，即当对象当前提供的信息不足以支撑决策时，采用延迟决策，等待更多信息来完成最终决策。所以，三支决策可以规避分类信息不足时盲目决策造成的风险。

三支决策在进行分类决策前，需对样本进行域的划分。划分的原理基于粗糙集理论。按照粗糙集的定义，根据元素x是否属于概念A，x与A将分为3 种关系：x∈A,x∈ ¬A,x∈BND(A)。由此，考虑一般分类问题，将元素x是否符合概念A作为分类标准，将可能会得到x∈BND(A) ， 即元素x属于概念A的边界域。由此，可得知决策粗糙集在 代价敏感分类问题上的整体思路。

在决策粗糙集公式化描述中，X是全集U的子集，状态集合可以表示为 Ω={X,¬X}，X和 ¬X分别表示属于X和不属于X。为了方便，子集和子集的状态都使用X来表示。状态X对应的动作集合为 ∧={P,B,N} ， 其中P、B、N分别表示3种判定动作，即x∈POS(X)、x∈BND(X)、x∈NEG(X)。三支决策的损失函数由各个动作带来的损失决定。如表1 所示，其中λPP、λBP、λNP表 示当x属于X时采取动作P、B、N产生的损失，λPN、λBN、λNN表示当对象属于 ¬X时采取动作P、B、N时产生的损失。

表1 三支决策的损失函数Table 1 Loss function of 3WD

根据最小风险决策规则：

(P)当Pr(X|[x])≥ α 时，x∈POS(X);

(B)当 β ＜Pr(X|[x])＜ α 时，x∈BND(X);

(N)当Pr(X|[x])≤ β 时，x∈NEG(X);

其中

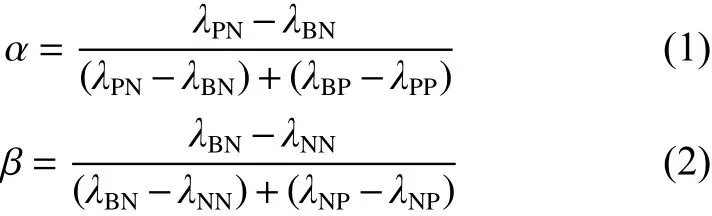
且

1.2 长短时记忆网络

LSTM 是由Hoehreiterhe 与Schmiduhber 于1997 年提出后经过大量的改进，目前被广泛应用[9]，成为目前处理序列与时序问题上的热门方案。LSTM 是由一般的RNN 改进而来。LSTM 与一般的RNN 的主要区别是在LSTM 中的神经元不再是由单纯的神经元组成而是由4 个功能不同的门来共同作用。其中包括了输入门、输出门、状态门，以及遗忘门。具体的结构如图1 所示。

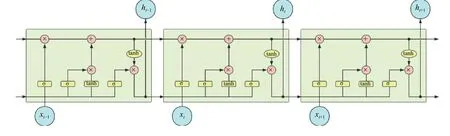
图1 LSTM 网络结构Fig.1 LSTM network structure

LSTM 的独特结构是为了使其能够解决长期依赖问题而专门设计的。不同于RNN 网络，LSTM 的重复结构是由更加复杂的3 个门相互连接而成。包括遗忘门、输入门与输出门。

式(4)～(9)描述了细胞内各个门的处理流程。

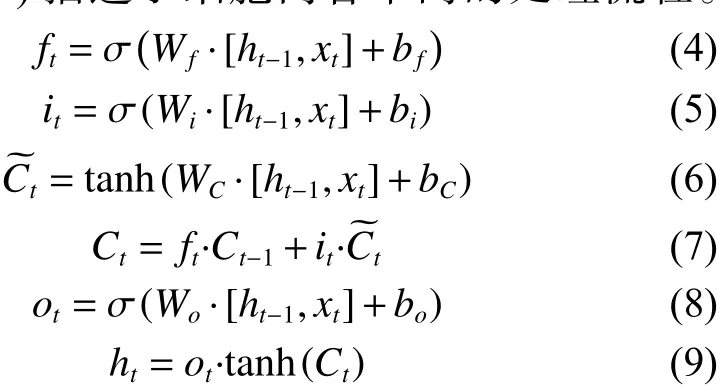
式(4)描述了遗忘门决定了当细胞更新时细胞状态会丢弃什么信息。该门会读取ht-1和xt，输出在 [0,1] 之间的数值与原先细胞状态Ct-1相结合。其中，1 表示完全保留，0 表示完全遗忘。其中，ht-1表示上一个细胞的输出，xt表示当前细胞的输入， σ 表示sigmod 函数。

式(5) 描述输入门决定了让多少新的信息加入到细胞状态中。第一步，细胞输入xt与细胞的上个输出ht-1会通过sigmod 元来决定更新的内容。

式(6)描述了更新内容。与式(5)同时，同样的输入会通过一个tanh 元，生成备用的更新内容。

式(7) 描述了更新内容Ct。将式(5) 与式(6)两部分结果相乘，将细胞状态由Ct-1更新至Ct。

最终输出数据由式(8)的输出与当前细胞状态的一部分共同决定输出的最终值，如式(9)描述。

以上为LSTM 模型的基本工作流。

1.3 代价敏感分类

一般的，对于分类算法的研究的核心与重点为如何取得更高的分类准确率，但事实上，只要有误差存在，分类过程总会产生代价。而代价敏感分类就是关注如何使分类过程中产生的代价最小。根据问题的难易程度，代价敏感问题常被分为二分类与多分类问题。对于二分类问题，目前大部分的代价敏感分类多是从非代价敏感分类算法加以转化得到的。

结合上述，可将代价敏感分类等价于一个优化问题: 将实例使用分类算法A划分至类别I时，使损失函数L(x,i) 达到最小[10]：

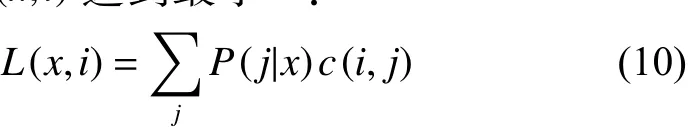
式中：x表示一个实例；L(x,i) 表示x的类别为i时错误分类的代价；P(j|x) 表示算法将x划分至类别j的概率；c(i,j) 表示将i分类划分至j所产生的代价。

对于每个类别i，L(x,i) 表示x所有可能的划分结果的代价的概率和。故由式(10)知，当分类代价最小时，其分类结果P(j|x) 不一定取到最大值。即为了得到更小的分类代价，可能会放弃最大的分类结果。

在如何使算法获得倾向性的问题上，有两种经典算法：1)通过预处理，使算法对某些结果具有敏感性，此方法称为rescaling[11]；2)希望通过以代价为基准修改不同分类在算法中的成员可能性，从而产生不同的倾向性。此方法称为reweighted[12]。

2 基于LSTM 的三支决策分类算法

基于三支决策的L S T M 算法在原有的LSTM 基础上，增加了三支决策步骤，对前端分类器给出的预测结果做出接受、拒绝、延迟3 种不同的方案，算法流程如图2 所示。

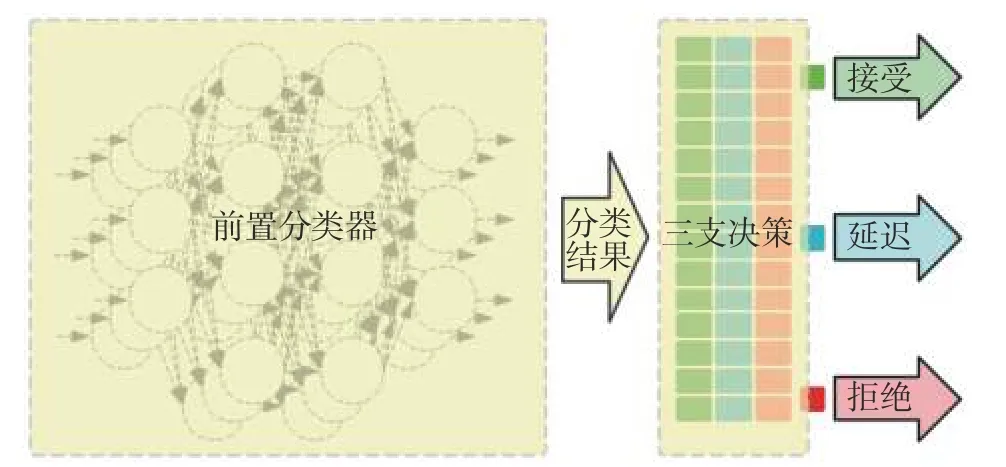
图2 基于LSTM 的三支决策算法流程Fig.2 Flow of 3WD based on LSTM

算法包括两部分：1) 前置分类器，用于初步分类；2) 三支决策，考虑决策风险，通过算法的判断降低决策风险。

2.1 前置分类器

前置分类器的作用主要体现在前置分类器的分类精度最终决定了整体上的分类效果。此后的三支决策对前置分类器的分类结果做出评判，决定接受、拒绝、或者延迟推断。对于LSTM 分类器，主要用来解决分类和时序问题预测。输出包括预测结果C和预测的分类概率p。分类概率p用于下一步中三支决策算法来判断是否采纳分类结果。

2.2 三支决策

三支决策对前置分类器给出的结果进行分析。根据式(1)～(3)，可以得出相应的判断代价 Ø。

将根据前置分类器的分类结果X，与由对应的损失函数 λ 计算出的代价，由判断规则(Pli)、(Bli)、(Nli)判断，给出相应的决策建议。

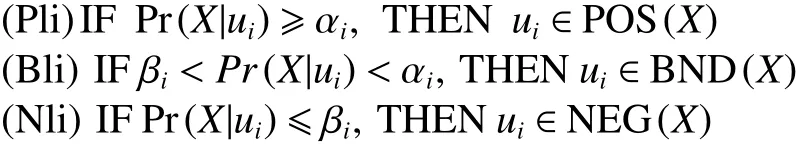
2.3 算法概述

结合上述分析，本文提出基于LSTM 与三支决策的代价敏感分类算法，算法描述如下：

BEGIN：

3 实验与结果

实验在自建实验平台中运行。实验平台包括4 台服务器，每台服务器均使用相同的配置。每台服务器有6 个CPU，主频2.5 GHz，运行内存16 GB。

测试数据集来自UCI 开放数据集中的Beijing PM2.5 Data Set 与International airline passengers。数据集均为分类任务。

PM2.5 数据集来自于UCI 数据库，该数据集记录了从2010 年1 月1 日至2014 年12 月31 日北京市的空气质量指数和气象数据。数据集为时间序列数据，特征为连续特征，任务可作为分类或回归任务。数据一共43 824 条记录，特征共13 个，部分数据缺失。

数据集中包括了时间，当日的温度、湿度、气压、风向、累计风速、累计降雨/降雪量、PM2.5 指数共13 个数据。其中的PM2.5 指数为当日PM2.5 值，为连续实数。当预测PM2.5 值时，问题为回归问题。若以判断PM2.5 区间作为空气质量判断时，问题为分类问题。本例中，将原数据集中的PM2.5 均分为4 个区间，从小到大分别标记为[优，良，一般，差]4 类。根据前tn-i的气象数据，预测tn的空气质量。

图3 表示了原数据集中，PM2.5 与气象数据的关系。图4 表示了两段分类结果的分布信息。

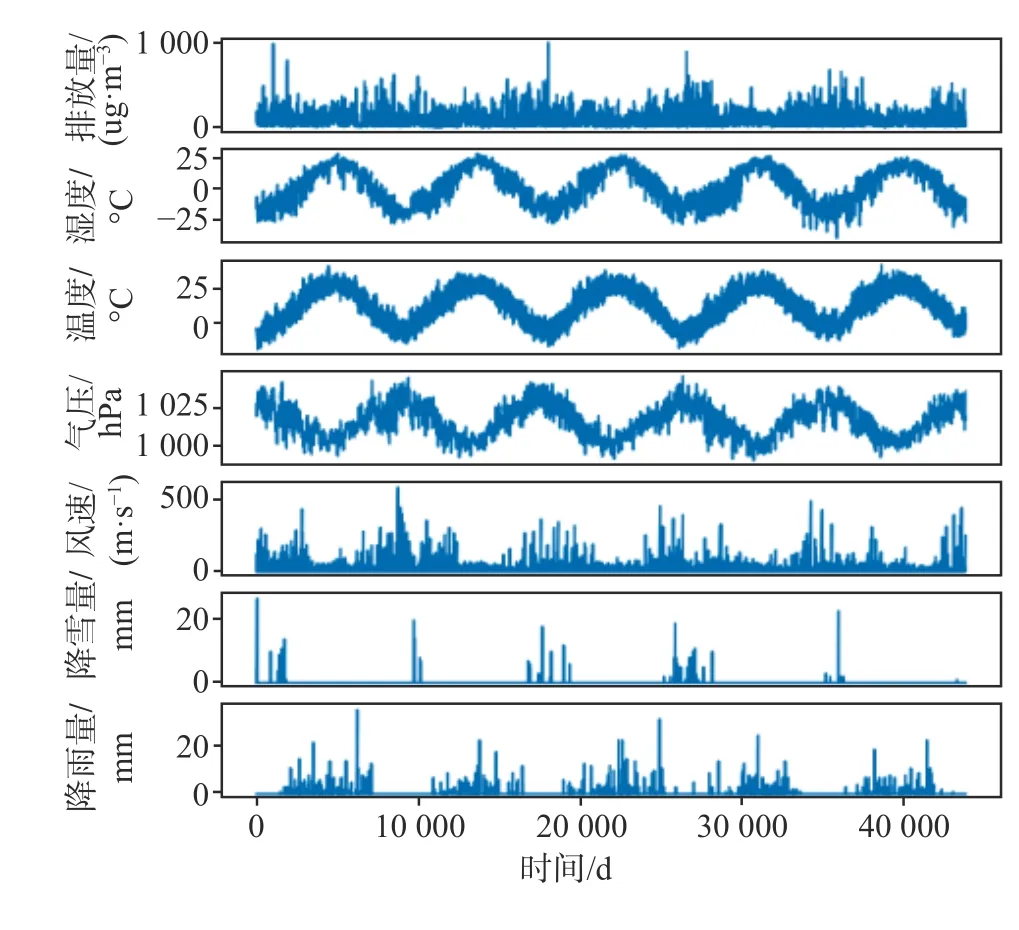
图3 原始数据集中的特征分布Fig.3 Frequency of features in this dataset

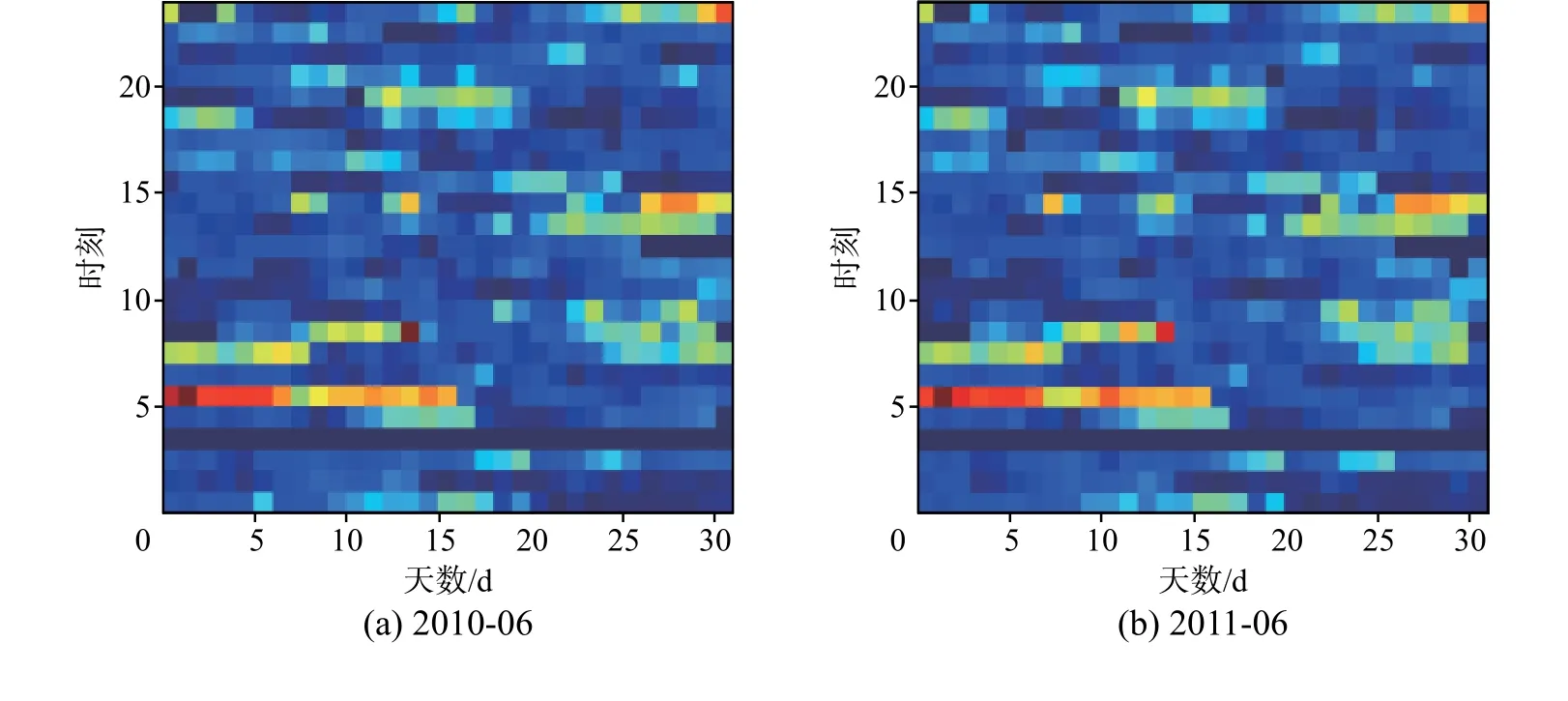
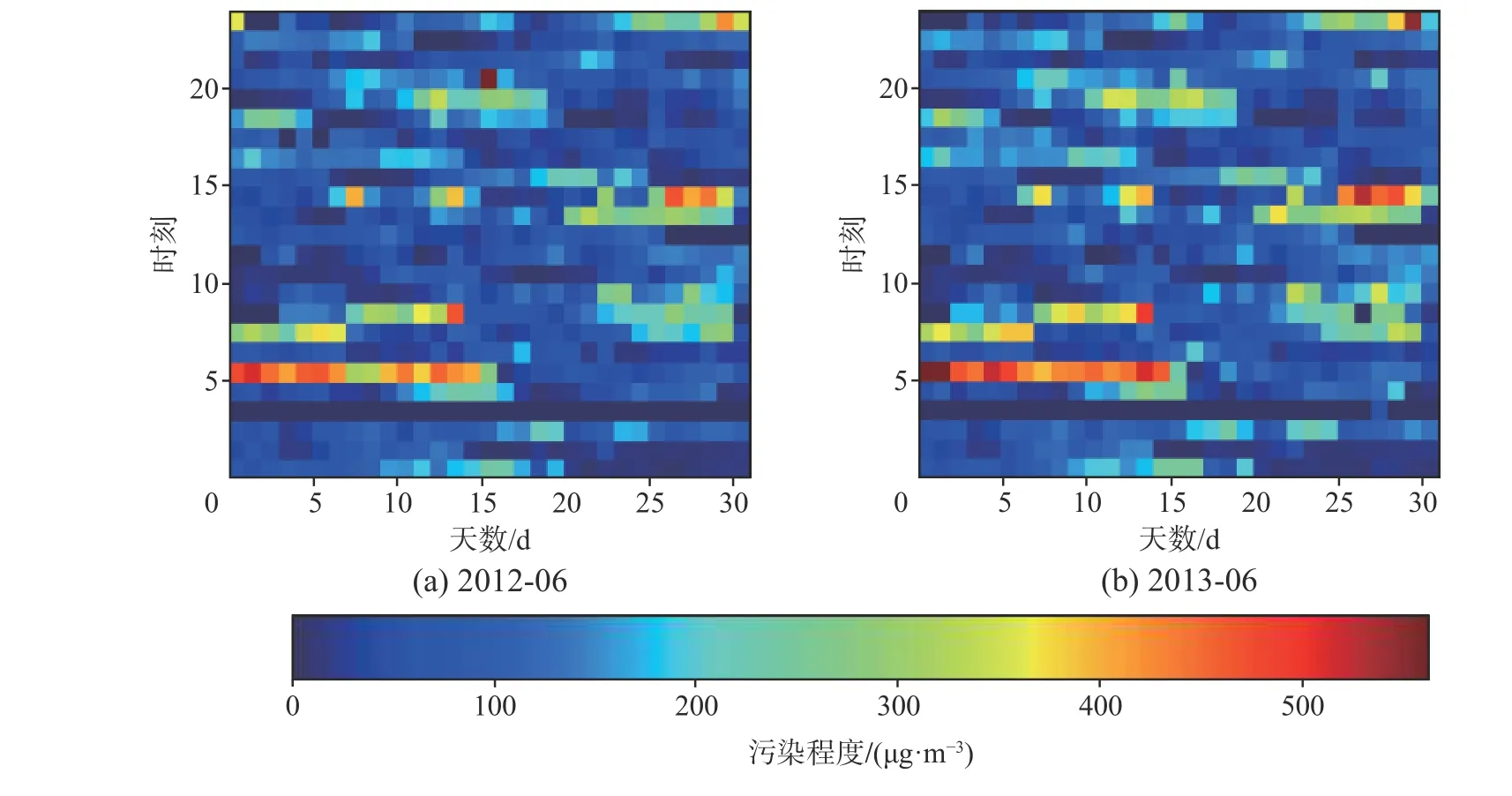
图4 原数据集中分类结果与时间的变化关系Fig.4 Relations between classify result and time change

从图4 可以看出，空气质量与时间有明显的关系，并且呈现出一定的周期规律。

国际旅行旅客数据集包括了1949—1960 年12 年之间每个月的国际航线航班旅客人数。共144 个数据，单位为1 千人。图5 为原数据集中数据的分布。

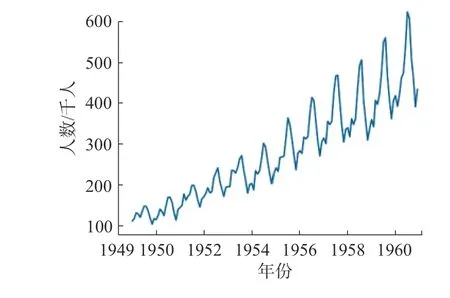
图5 1949—1960 年国际航班旅客人数Fig.5 Number of international airline traveler between 1949—1960

3.1 PM2.5 数据集

根据前述对数据集的分析，将数据通过前置分类器进行回归分析，得到分类结果。此LSTM分类器在数据集上的分类准确率为0.997。由于为多分类问题，参考指标由准确率−召回率改为混淆矩阵。此分类器在测试数据上的结果混淆矩阵见图6。图7 为分类器训练的最终损失函数。

设代价函数为：

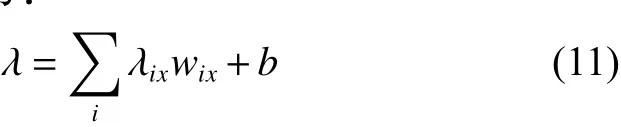
式中： λix为判断是否正确；wix为权重；即判断代价；b为偏移值。 λix的计算方式由表1 所述代价函数计算可得。

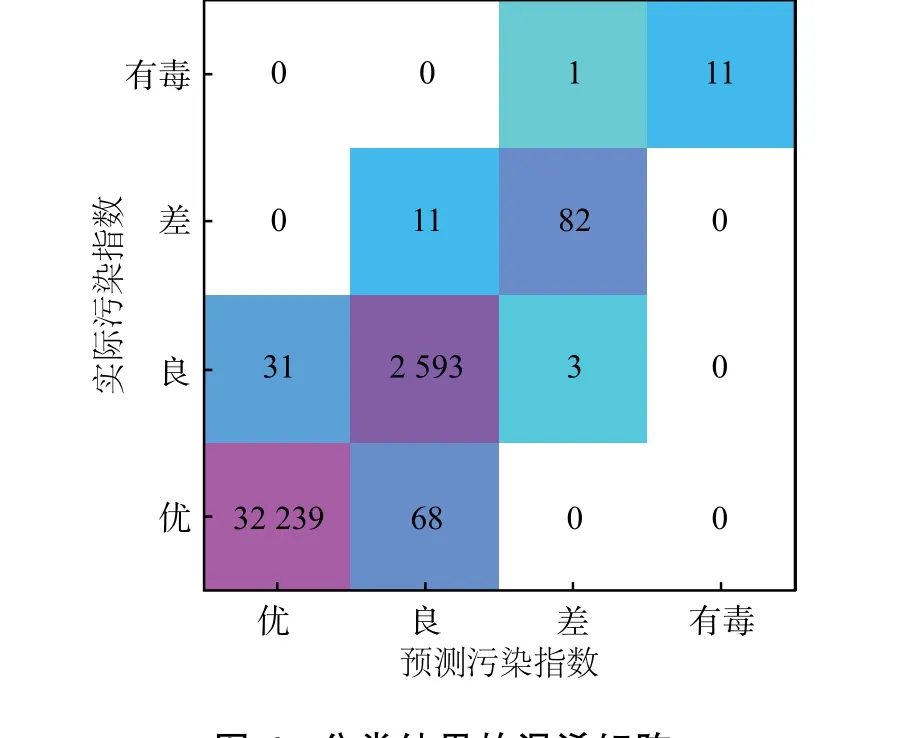
图6 分类结果的混淆矩阵Fig.6 Confusion matrix of classification result

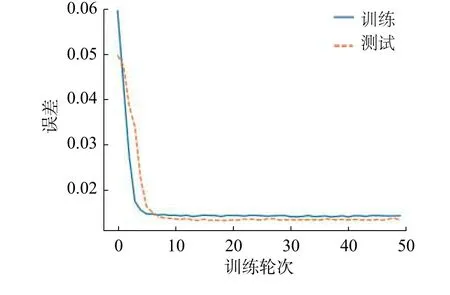
图7 LSTM 训练损失Fig.7 Loss of LSTM training

将预测结果代入式(11)后, 得到原分类器的决策代价。

将得到的损失偏差与代入三支决策的决策规则 (Pli、Bli、Nli) 中，对明显偏离预测中心的值进行标记，得到新的分类代价。

表2 可知，使用三支决策算法进行判断的分类任务在代价优化上有显著作用。

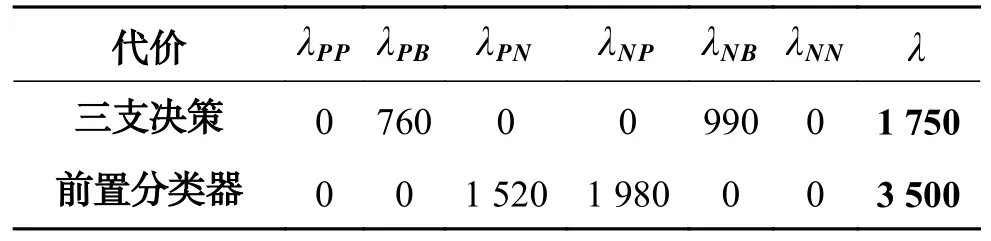
表2 使用三支决策的分类代价与未使用三支决策的分 类代价对比Table 2 Compara of cost of classification between 3WD and non-3WD

3.2 国际旅行旅客人数数据集

根据前述数据集的基本信息，将数据集进行前期分类。图8 为LSTM 作为前置分类器的预测数据。取预测步长为3，预测网络两层，每层含128 个LSTM 单元。

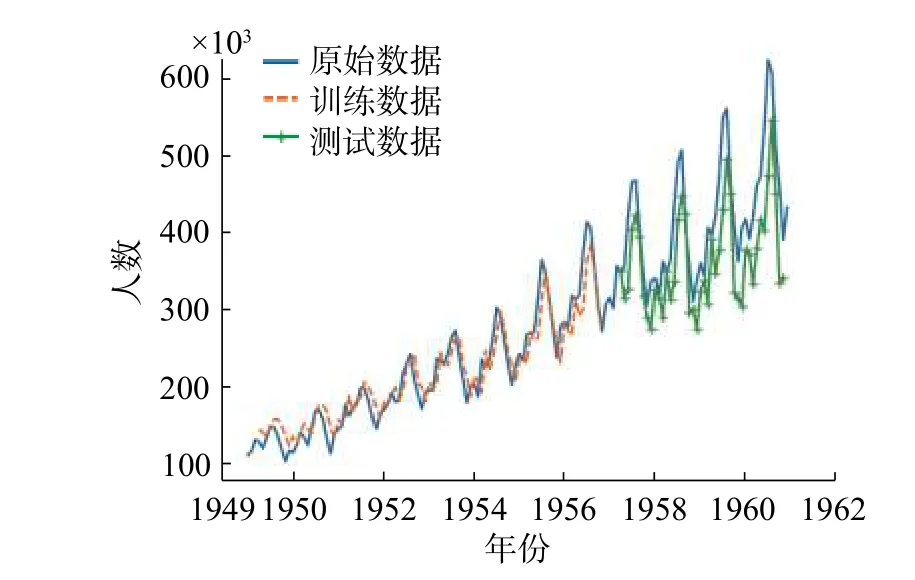
图8 经过前置分类器的预测数据Fig.8 Predict data after preprocessing

显然，随着时间推移，距预测点较远的点预测误差越大。在整个数据集上，前置分类器的测试数据均方误差为28.03。

对于回归问题，由于没有直接的方式判断分类的正误，本文使用均方误差来描述对应的置信度。由此，相应的代价函数可表示为

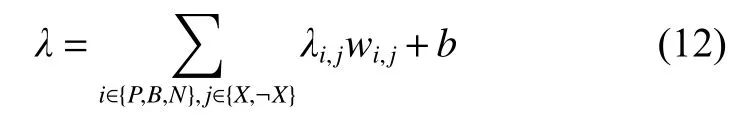
但是与前述判断规则(Pli、Bli、Nli)不同，此时的分类不再是由有限的状态集合 {X,¬X} 描述，而是由偏差和 方差组成的连续集合。所以，此时的(代) 价 λi,j不再是确定的函数而是与由均方差 MSEθˆ 描述的模型和距离预测点t的两者组成的概率分布。

式中：f为训练模型的偏差分布；为模型的均方差；tn为当前点距预测点的距离。

本例中，为方便计算，假设分布f为均匀分布。此时，代价函数简化为只与时间tn相关的函数。由此，代入假设条件，可以得到如图9 的代价曲线。

将代入三支决策算法结果如图9。由结果可知，对于问题中给定时刻t， 在t+12 时，代价第一次大于阈值 α ，故在 [t,t+12] 时刻的数据是可信的。同理，在 [t+26] 时，预测代价第一次大于阈值 β ，所以从t+26 时刻起，预测数据不再可信。图10 表示t与代价之间的关系。

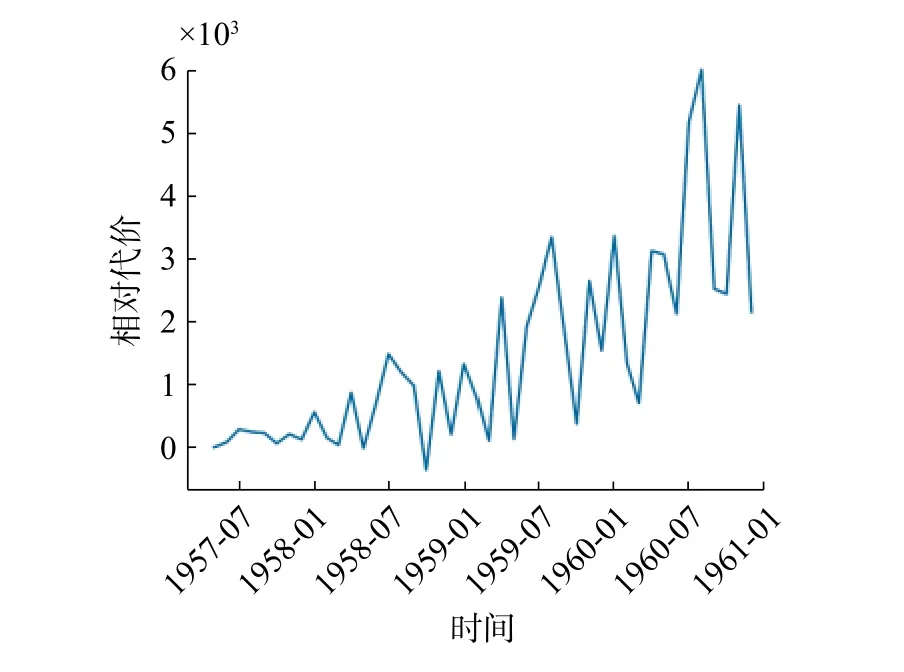
图9 随 tn 而代价越来越大的判断曲线 λtFig.9 As tn increases, the prediction results become more and more inaccurate

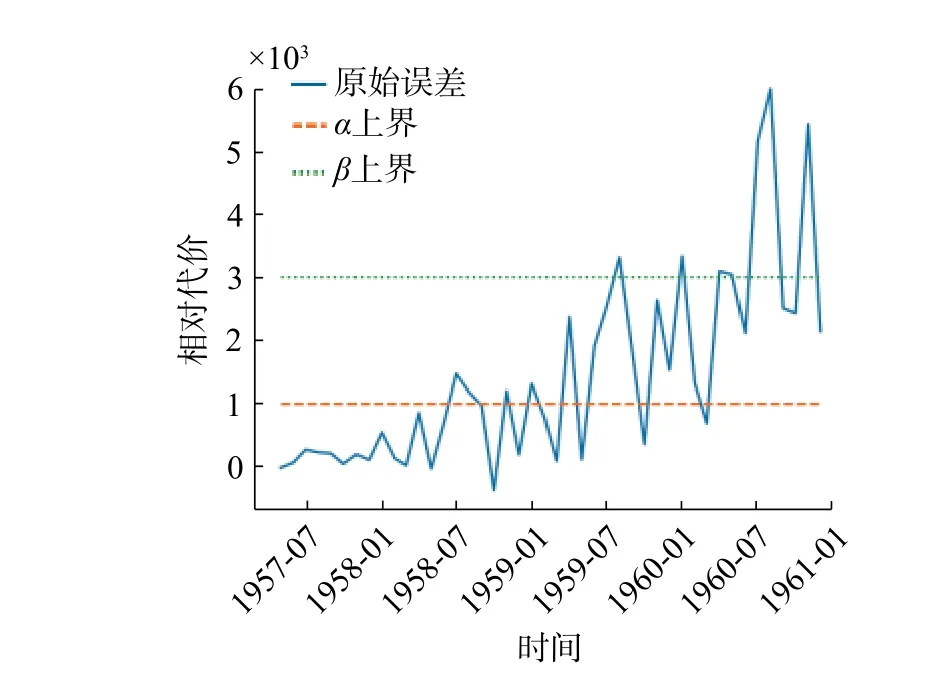
图10 代价判断决定的三支决策结果Fig.10 Discarding costly predictions given by 3WD

4 结束语

本文通过两个实验的验证，提出了基于LSTM 的三支决策分类算法。实验1 在LSTM 分类的基础上，增加三支决策分类后明显地降低了决策风险；实验2 在原先分类器中引入三支决策后，也有了代价上的优化。实验表明：1)三支决策的决策准确率受前端分类器准确率的较大影响；2)三支决策算法可以结合深度学习模型解决代价敏感分类问题，而非仅限于非贝叶斯模型的分类器；3)三支决策在解决代价敏感分类问题的同时，可以通过扩展代价定义的方式，为回归模型建立可信度判据。结合三支决策理论，在时间序列分析问题中，三支决策模型可以为预测结果增加可信度的判据，使得预测结果更加具有分析和处理的价值。

但是当前的工作只是初步的验证有关于深度学习与三支决策相结合形成新的代价敏感分类的初步研究。本文的研究尚处于初步的阶段。未来，对于模型的改进仍有许多研究空间。例如，对于三支决策算法，可以结合新的边界理论，形成自动化的边界确定；在整体模型中，可以借助boost 或专家分类器等模型，提出更完善的理论；以及结合Alex-net 等其他更高效的分类器来进一步提高前置分类器的性能等。这些改进都将能够进一步提高三支决策在在代价敏感分类领域的应用频率。