基于多粒度结构的网络表示学习

张蕾，钱峰，赵姝，陈洁，张燕平，刘峰

（1.安徽大学 计算机科学与技术学院，安徽 合肥 230601; 2.铜陵学院 数学与计算机学院，安徽 铜陵 244061）

研究人员常用网络(图)描述不同学科领域中实体间的交互关系，例如生物学领域中的蛋白质互联网络，社会学领域中的社交网络，语言学领域中的词共现网络。结合不同的分析任务对网络进行研究、探索，进而挖掘出隐藏在网络数据中的信息，使之服务于人类。不过，真实场景中的网络数据通常具有稀疏、高维等特质，直接利用这样的数据进行分析通常有较高的计算复杂度，使得许多先进的研究成果无法直接应用到现实的网络环境中。

网络表示学习[1](network representation learning，NRL)是解决上述问题的有效方法，旨在保留结构信息的前提下，为网络中的每个节点学习一个低维、稠密的向量表示。如此，网络被映射到一个向量空间中，并可通过许多经典的基于向量的机器学习技术处理许多网络分析任务，如节点分类[2]、链接预测[3]、节点聚类[4]、可视化[5]、推荐[6]等。

网络表示学习不仅要解决网络数据的高维和稀疏的问题，还需使学习到的节点特征表示能够保留丰富的网络结构信息。网络中的节点结构大致分为三类：1)微观结构，即局部相似性，例如：一阶相似性(相邻)、二阶相似性(有共同的邻居)。2)中观结构，例如：角色相似性(承担相同的功能)、社团相似性(属于同一社团)。3) 宏观结构，即全局网络特性，例如：无标度(度分布符合幂律分布)特性、小世界(高聚类系数)特性。

为获取有效的节点表示，结合最先进的机器学习、深度学习等技术，已提出各种各样的网络表示学习方法。DeepWalk[7]和Node2Vec[8]通 过随机游走获取节点的局部相似性。GraRep[9]和Walklets[10]通过将邻接矩阵提升到k次幂获取节点的k阶相似性。DNGR[11]通过随机冲浪策略获取节点高阶相似性。Struc2Vec[12]通过构造层次加权图，并利用层次加权图上的随机游走获取节点的结构相似性。M-NMF[13]通过融合模块度[14](modularity)的非负矩阵分解(nonnegative matrix factor，NMF)方法，将社团结构信息纳入网络表示学习中。GraphWave[15]通过谱图小波的扩散获取节点的角色结构相似性。HARP[16]通过随机合并网络中相邻节点，迭代地将网络粗化为一系列简化的网络，然后基于这些简化的网络递归地构建节点向量，从而捕获网络的全局特征。

最近，图卷积网络[17](graph convolutional networks，GCN)越来越受到关注，已经显示GCN 对网络分析任务性能的改进有着显著的效果。GCN 通过卷积层聚合网络中每个节点及其邻居节点的特征，输出聚合结果的加权均值用于该节点新的特征表示。通过卷积层的不断叠加，节点能够整合k阶邻居信息，从而获取更高阶的节点特征表示。尽管GCN 的设计目标是利用深层模型更好地学习网络中节点的特征表示，但大多数当前方法依然是浅层结构。例如，GCN[18]实际上只使用两层结构，更多的卷积层甚至可能会损害方法的性能[19]。而且随着模型层数的增加，学习到的节点特征可能过度平滑，使得不同簇的节点变得无法区分。这样的限制违背使用深层模型的目的，导致利用GCN 模型进行网络表示学习不利于捕获节点的高阶和全局特征。

为克服这种限制，受商空间[20]中的分层递阶[21]思想的启发，提出一种基于多粒度结构的网络表示学习方法(network representation learning based on multi-granularity structure，Multi-GS)。Multi-GS 首先基于模块度[22]和粒计算[23]的思想，利用网络自身的层次结构，即社团结构，通过使用局部模块度增量迭代地移动和合并网络中的节点，构造网络的粗粒度结构。利用粗粒度的结构生成更粗粒度的结构，反复多次，最终获得分层递阶的多粒度网络结构。在多粒度结构中，不同粗细的粒能够反映节点在不同粒度空间上的社团内邻近关系。然后，Multi-GS 使用无监督的GCN 模型分别学习不同粒度空间中粒的特征表示向量，学习到的特征能够反映不同粒度下粒间的邻近关系，不同粗细粒度中的粒间关系能够表示不同阶的节点关系，粒度越粗阶数越高。最后，Multi-GS 将不同粒度空间中学习到的粒特征表示按照由粗到细的顺序进行逐层细化拼接，输出最细粒度空间中拼接后的粒特征表示作为初始网络的节点特征表示。实验结果表明，结合多粒度结构能使GCN 有效地捕获网络的高阶特征，学习的节点表示可提升诸如节点分类任务的性能。

1 问题定义

定义1设网络G=(V,E,A)， 其中，V代表节点集合，E代表边集合，A代表邻接矩阵。记vi∈V代表一个节点，eij=(vi,vj)∈E代表一条边，邻接矩阵A∈Rn×n表示网络的拓扑结构 ，n=|V|，若eij∈E，则Aij=wij＞0 ；若eij∉E，则Ai j=0。记代 表 节 点vi的 度 ， Γ(vi)={vj|eij∈E} 代表节点vi的邻居节点集合。

定义 2网络的模块度[22]Q定义为

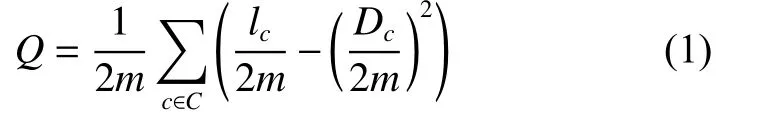
式中：m表示网络中的边的总数；lc表示社团c中所有内部边的总数表示社团c中所有节点的度的总和；C表示所有社团构成的集合。在社团挖掘任务中，通常使用模块度评价社团划分的效果，模块度Q值越高，表明社团划分的效果越佳。

基于式(1)，可以推导出两个社团合并后的局部模块度增量 ΔQ。设当前划分中的任意两个社团p和q， 合并p和q后的社团为k，产生的局部模块度增量 ΔQpq的计算方法如下：

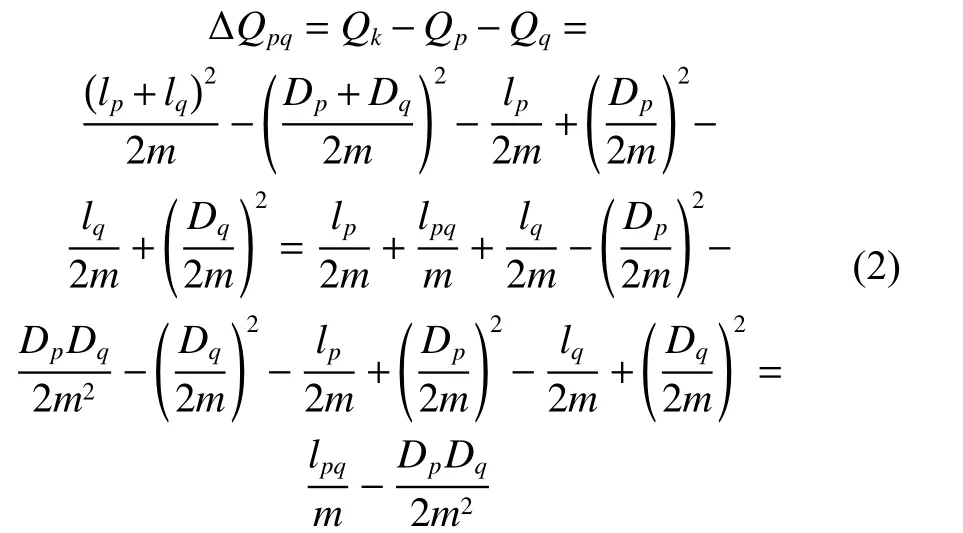
定义3给定初始网络G(0)。在粒度世界中，网络中的每个节点可视为一个基本粒。同样用边描述粒间的关系。通过粒度衡量粒的大小(粗细)。基本粒是指最细粒度的粒。粒化是指将多个粒合并为一个更粗粒度的粒的操作。

将初始网络结构视为由基本粒构成的最细粒度的粒层结构。粒化分层是通过聚合和粒化操作，迭代地形成粒度由细到粗的多粒层结构。具体地说，通过不断聚合不同粒层中的粒和边，G(0)被递归压缩成一系列粒度由细到粗的粒层，如图1 所示。

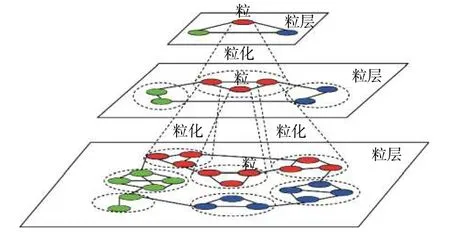
图1 网络拓扑的粒化分层示例Fig.1 An example of hierarchical view of network topology

定义4给定网络G，网络表示学习的目标是将网络中的节点vi∈V映射到低维向量zi∈Rd，其中，d表示向量的维度，d≪n。学习到的向量表示可客观反映节点在原始网络中的结构特性。例如，具有相似结构的节点在特征向量的欧式距离空间中彼此靠近，不相似的节点彼此远离。

2 网络表示学习方法Multi-GS

Multi-GS 首先基于模块度构建多粒度的网络分层结构；接着使用GCN 模型依次学习不同粒层中所有粒的特征向量；然后自底向上逐层对粒的特征向量进行映射、拼接；最后输出最终的结果作为初始网络中节点的特征表示，如图2 所示。

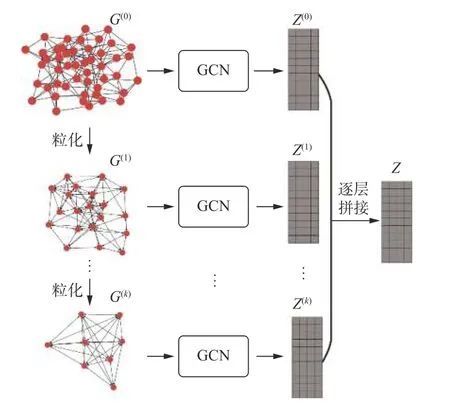
图2 Multi-GS 方法的框架Fig.2 Framework of Multi-GS approach

2.1 基于模块度的网络粒化分层

本小节介绍Multi-GS 的粒化分层操作。主要包含两个步骤：1)粒的移动与合并：移动和合并的决定取决于局部模块度增量计算结果。2) 粒化：生成更粗粒度的粒层结构。相关细节见算法1。

算法1 网络粒化分层(Graphgranular)

输入网络G=(V,E)，最大粒化层数k；

输出由细到粗的粒层 G r(0),Gr(1),···,Gr(k)。

10)将粒vi从自身所在的集合中移出；

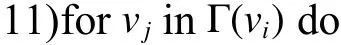
12)按式(2)计算粒vi移入集合Cj后的模块度增量 ΔQ；

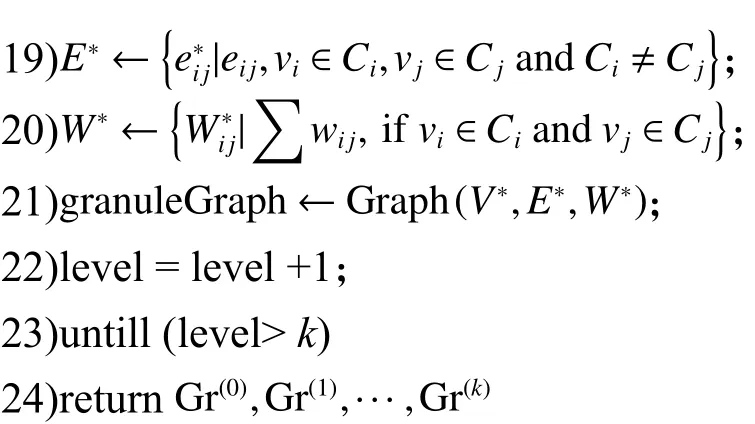
算法1 的主要步骤如下：

粒的移动与合并：首先将当前粒层中的每个粒放入不同的集合中(第6 行)。其中，子集合的数量等于当前粒层中粒的数量。遍历所有的粒(第9 行)，将当前粒移出自身所在的集合(第10行)，依次移入一个相邻粒的集合中，并依据式(2)计算移入后的局部模块度增量 ΔQ(第11～13 行)。待与所有相邻粒集合的 ΔQ计算完成后，选择与最大(正值)模块度增量相关联的相邻粒集合，并将粒并入该集合中(第14 行)。遍历结束后，重新计算模块度Q(第16 行)。当未达到模块度的局部极大值时，重复上述步骤(第8～16 行)。

在第2 个步骤中，新粒间的边权由两个对应集合中的粒间的边权和确定。同一集合中粒间的内部边视为新粒的自边。

2.2 基于图卷积网络的粒特征表示学习

本小节介绍Multi-GS 的GCN 模型结构，包括两个部分，编码器和解码器，如图3 所示。GCN模型借鉴VGAE[24]的设计，Multi-GS 不使用节点的辅助信息，仅利用网络的拓扑结构学习节点的特征表示，因此，最终的GCN 模型在设计上与VGAE 有所区别。

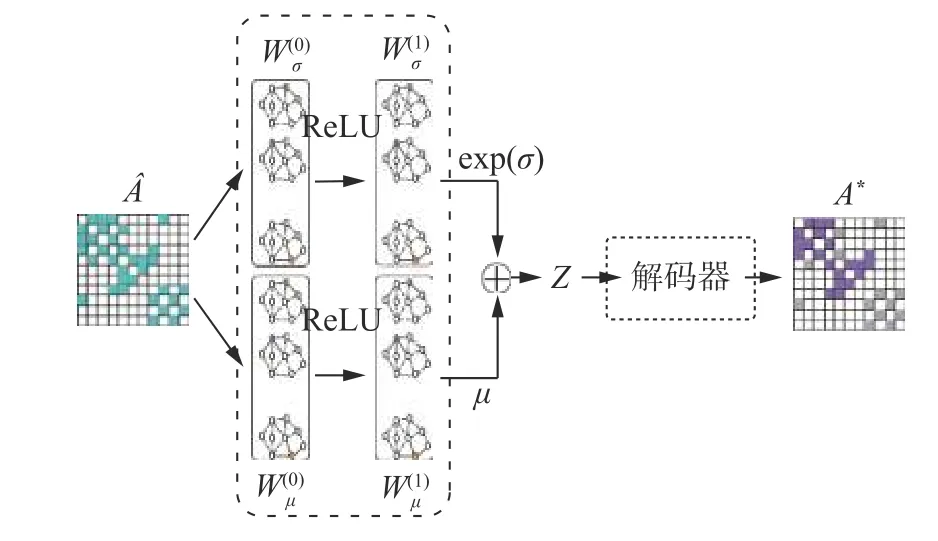
图3 图卷积神经网络模型结构Fig.3 The structure of GCN model

GCN 模型的输入是不同分层中的粒关系矩阵A，A∈RN×N表示同一粒层中粒间的连接关系，其中，N表示粒的数量。给定粒i和粒j，则Ai j=wij，wi j表示粒i和粒j间的连接权重。首先，利用式(3)计算得到归一化的矩阵

其中，f(•) 表示线性激活函数，第一层使用RELU函数，第二层使用sigmoid 函数；µ 和 σ 分别表示向量矩阵Z的均值向量矩阵和标准差向量矩阵；是需要训练的权重矩阵；可通过对 µ 和 σ 进行采样得到特征矩阵Z，Z=µ+ε∗exp(σ),ε ～N(0,I) ；“*”符号表示两个向量的内积。

基于变分推断的编码器，其变分下界的优化目标函数如下：

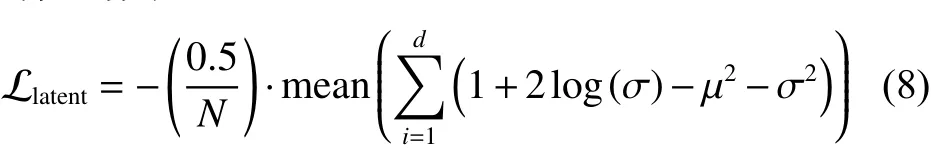
解码器使用式(7)重构关系矩阵A，对于重构损失，考虑到A的稀疏性，使用加权交叉熵损失函数Loss 构建最终的目标函数，具体公式如下：

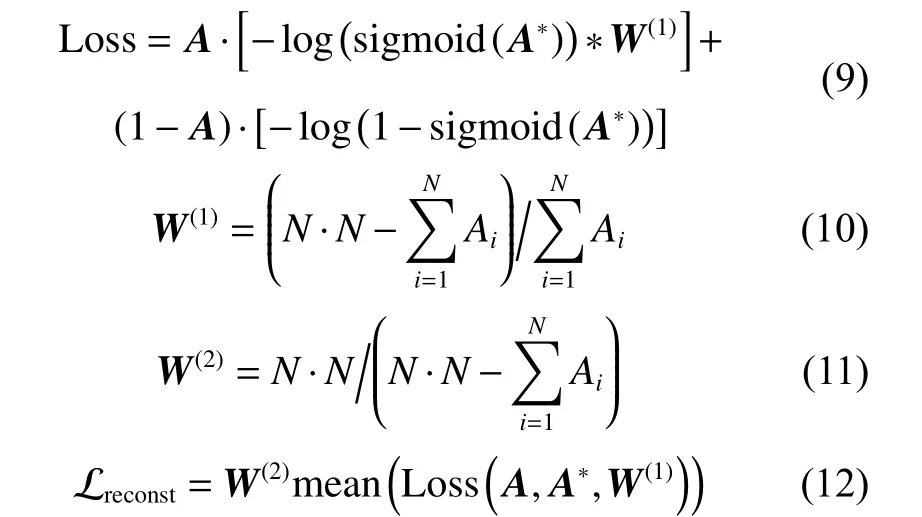
结合式(8)和式(12)，GCN 模型最终的目标函数如下：

2.3 算法描述

本小节介绍基于多粒度结构的网络表示学习方法Multi-GS，主要包括3 个步骤：利用局部模块度增量 ΔQ，由细到粗地构造多粒度的网络分层结构(已在2.1 小节详细介绍)；使用GCN 模型(已在2.2 小节详细介绍)学习不同粒层中粒的特征表示；将不同粒层的粒特征表示由粗到细地进行逐层拼接，最终得到最细粒度粒层中粒的特征表示；输出此结果作为初始网络的节点特征表示。相关细节见算法2。

算法2基于多粒度结构的网络表示学习(Multi-GS)

输入网络G，粒化层数k，节点表示向量维度d，GCN 参数 Θ；

输出网络表示Z。

首先，Multi-GS 算法的输入包括3 个部分：网络G；粒化层数k；GCN 模型的参数 Θ，包括，节点表示向量维度d、训练次数和学习率。算法2 的第1 行，使用算法1 构建多粒度的网络分层结构，其复杂度为O(M+N)，其中M为每轮迭代中粒的数量，N是粒层中的边的数量。第2～第4 行，依次将不同粒层的粒关系矩阵A作为输入，利用GCN 模型学习粒的特征表示。GCN 模型的复杂度与网络的边数呈线性关系，其复杂度为O(mdh)，其中m是矩阵A中非零元素的数量，d是特征维数，h是权重矩阵的特征映射数量。另外，方法还需重建原始拓扑结构，因此总体复杂度为O(mdH+N2)，其中H是不同层上所有特征映射的总和。第5～第8 行，将学习到的粒特征向量由粗到细地进行拼接。其中，projection 函数是粒化过程的反向操作。在此过程中，上层的粒特征向量被映射到一个或多个较细粒度粒特征向量，投影结束后，拼接相同粒的两个不同的粒特征表示。循环结束后，得到基本粒的拼接后的特征表示，其复杂度为O(M)。第9 行，以基本粒的特征表示作为对应节点的特征表示进行输出。

3 实验和结果分析

本节通过节点分类和链接预测任务，在真实数据集上与4 个具有代表性的网络表示学习方法进行对比，验证Multi-GS 的有效性。实验环境为：Windows10 操作系统，Intel i7-4790 3.6 GHz CPU，8 GB 内存。通过Python 语言和Tensor-Flow 实现Multi-GS。

3.1 实验设定

1) 数据集。

实验使用5 个真实数据集，包括引文网络、生物网络、词共现网络和社交网络，详细信息见表1。Cora[25]是引文网络。其中，节点代表论文，根据论文的不同主题分为7 类。边代表论文间的引用关系。该网络包含2 708 个节点和5 278 条边。Citeseer[25]同样是引文网络。该网络包含6 类的3 312 种出版物。边代表不同出版物间的引用关系，共有4 660 条边。PPI[26]是生物网络。该网络包含3 890 个节点和38 739 条边。其中，节点代表蛋白质，根据不同的生物状态分为50 类，边代表蛋白质间的相互作用。WiKi[27]是维基百科数据库中单词的共现网络。该网络包含4 777 个节点，92 517 条边，以及40 种不同的词性标签。Blog-Catalog[28]是来自BlogCatalog 网站的社交网络。节点代表博主，并根据博主的个人兴趣划分为39类，边代表博主间的友谊关系。该网络包含10 312个节点和333 983 条边。

2) 对比算法。

实验选择4 种具有代表性的网络表示学习算法作为对比算法，包括DeepWalk、Node2Vec、GraRep、DNGR。关于这些方法的简要描述如下：

DeepWalk[7]：使用随机游走获取节点序列，通过SkipGram 方法学习节点表示。

Node2Vec[8]：类似于DeepWalk，但是使用有偏向的随机游走获取节点序列。

GraRep[9]：通过构造k步概率转移矩阵学习节点表示，能够保留节点的高阶相似性。

DNGR[11]：使用随机冲浪方法获取节点的高阶相似性，利用深度神经网络学习节点表示。

3) 参数设定。

对于Multi-GS 方法中的GCN 模型，使用Adam 优化器更新训练中的参数，学习率设为0.05。对于DeepWalk 和Node2Vec，节点游走次数设为10，窗口大小设为10，随机游走的长度设为80。Node2Vec 的参数p=0.25、q=4。对于GraRep，kstep=4。对于DNGR 的随机冲浪方法，迭代次数设为4，重启概率 α =0.98，自编码器的层数设为2，使用RMSProp 优化器，训练次数设为400，学习率设为0.002。为进行公平比较，所以方法学习的节点表示维度均设为128。

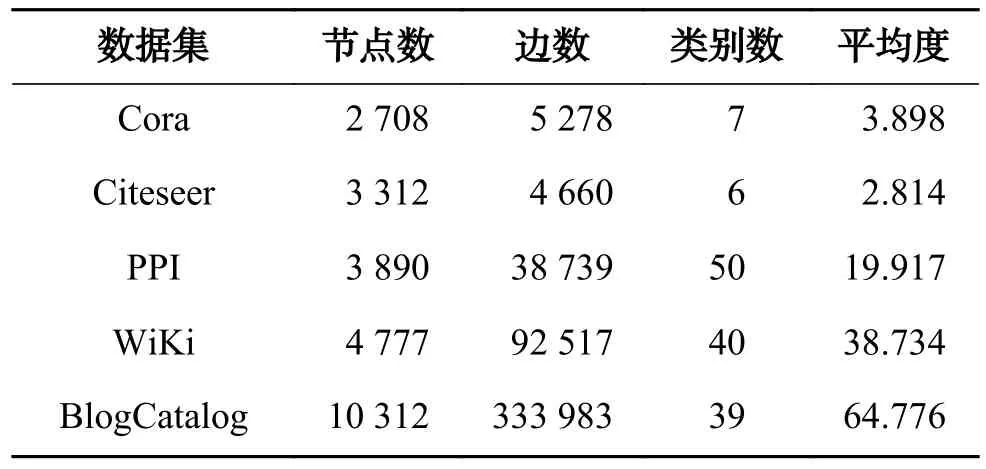
表1 数据集信息Table 1 Datasets information

3.2 节点分类

利用节点分类任务比较Multi-GS 和对比算法的性能差异。实验挑选4 种不同领域数据集，包括Citeseer、PPI、WiKi 和BlogCatalog。首先各自使用网络中所有节点学习节点的特征表示，对于Multi-GS，为比较不同的粒化层次对方法性能的影响，针对不同的数据集，分别设置5 组实验，在每组实验中，将粒化层次从0 设到4(k为0～4)。k=0 表示Multi-GS 不使用多粒度结构进行联合学习表示，仅利用原始网络通过GCN 模型学习节点的表示。针对节点分类，使用Logistic 回归分类器，随机从不同数据集中分别选择{10%，50%，90%}节点训练分类器，在其余节点上评估分类器的性能。为衡量分类性能，实验采用Micro-F1

[29]和Macro-F1[29]作为评价指标。两个指标越大，分类性能越好。所有的分类实验重复10次，报告平均结果。表2～5 分别展示在Citeseer、PPI、WiKi 和BlogCatalog 数据集上的节点分类Micro-F1和Macro-F1的均值，其中，粗体表示性能最好的结果，下划线表示对比算法中性能最优的结果。

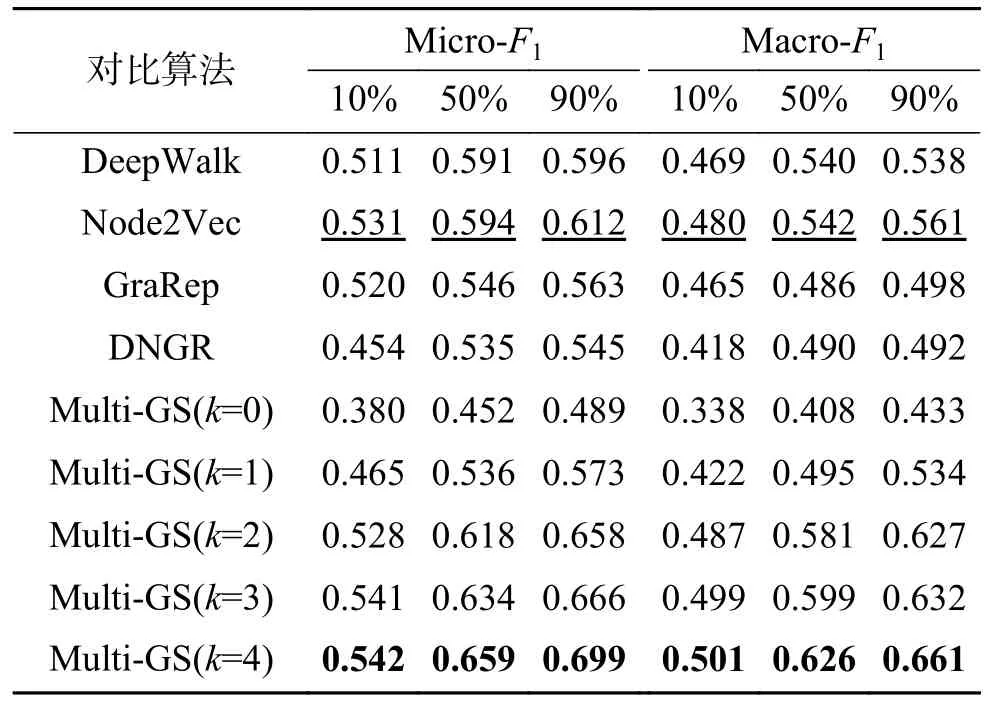
表2 Citeseer 数据集上的Micro-F1 和Macro-F1 结果Table 2 Micro-F1 and Macro-F1 results on Citeseer dataset

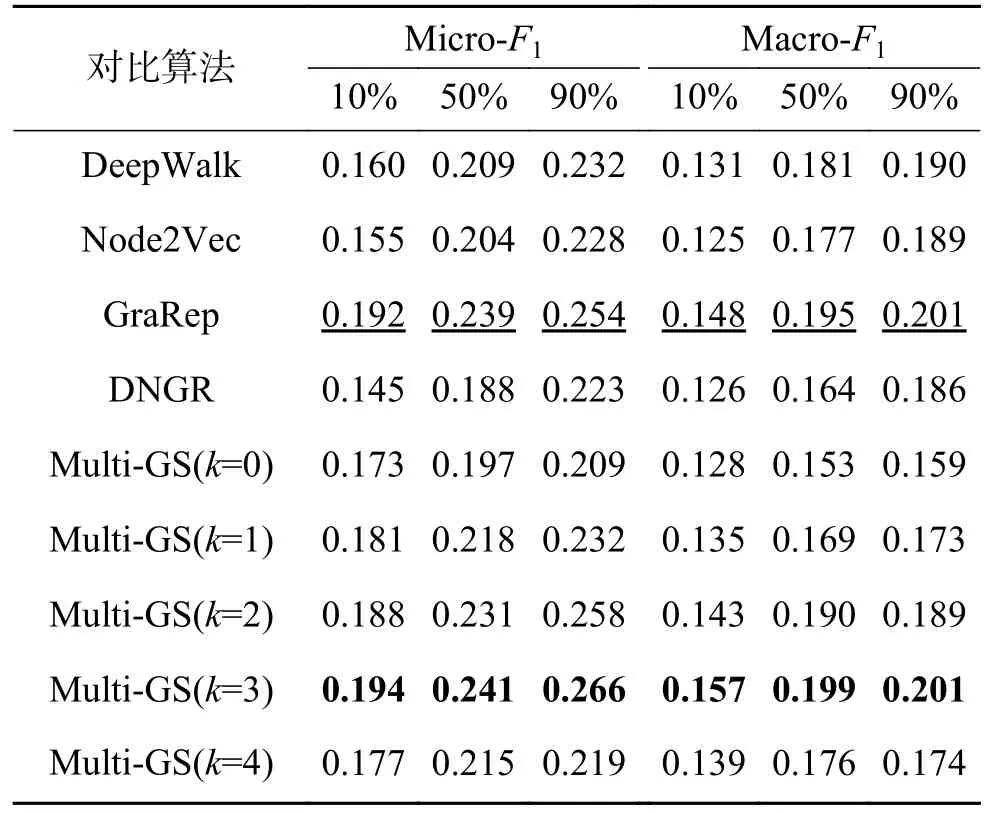
表3 PPI 数据集上的Micro-F1 和Macro-F1 结果Table 3 Micro-F1 and Macro-F1 results on PPI dataset

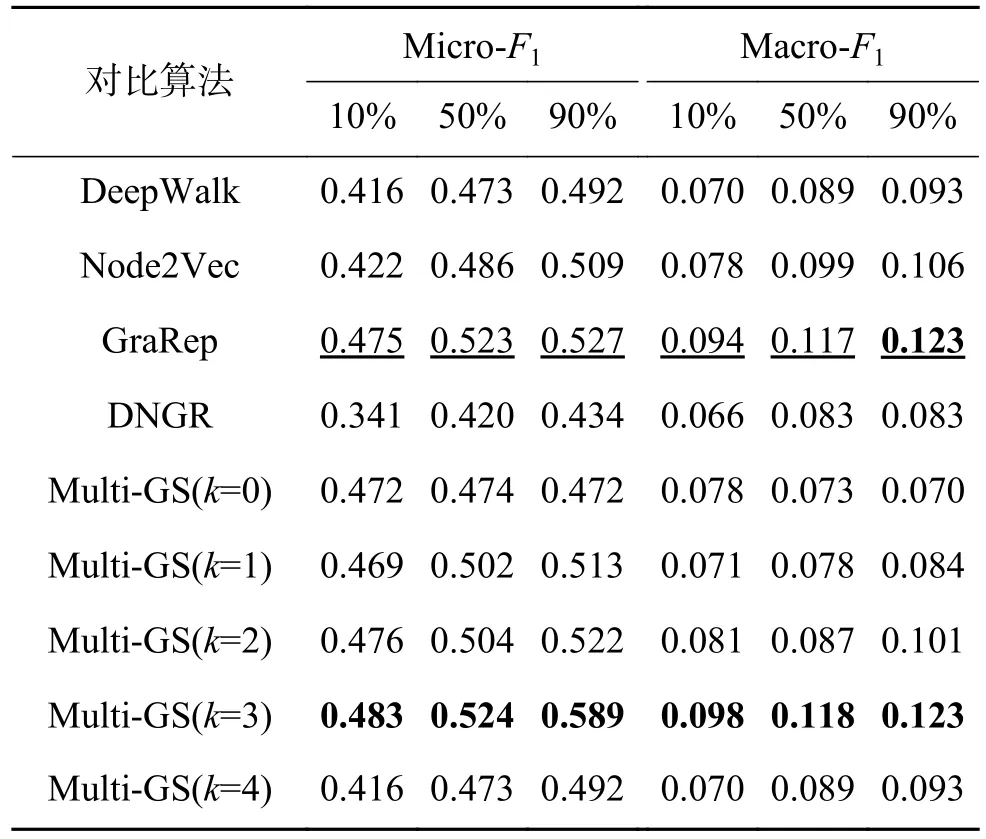
表4 WiKi 数据集上的Micro-F1 和Macro-F1 结果Table 4 Micro-F1 and Macro-F1 results on WiKi dataset

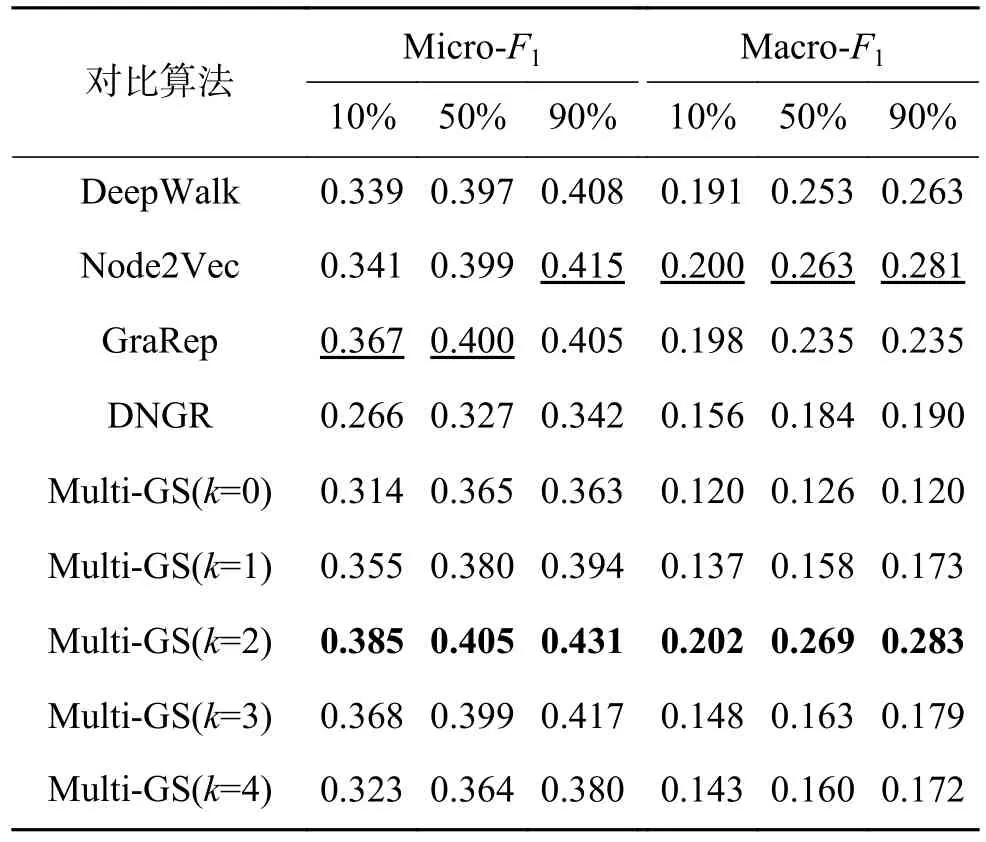
表5 BlogCatalog 数据集上的Micro-F1 和Macro-F1 结果Table 5 Micro-F1 and Macro-F1 results on BlogCatalog dataset

实验结果显示，在对比算法中，GreRap 表现出强有力的竞争力，Node2Vec 也表现不俗。因无法获取节点的一阶相似性，故DNGR 表现较差。针对Multi-GS，可以发现，相对于不使用联合学习(k=0)的情形，使用多粒度结构在多数情况下可提升方法的性能，说明保留节点的高阶相似性可提升节点分类任务的性能。对于相同的数据集，Multi-GS 在不同的粒化层次下存在差异。具体来说，在Citeseer 数据集上，随着粒化层数的增加，Multi-GS 的Micro-F1 和Macro-F1 值逐渐增大。在PPI 和WiKi 数据集上，最佳的结果出现在k=3 时。在BlogCatalog 数据集上，当k=2 时方法性能最好。依据表1 中不同数据集平均度的统计结果，可以看出，Citeseer 数据集的平均度是3.898 1，说明该网络是一个弱关系网络，BlogCata-log 数据集的平均度高达64.775 6，是一个强关系网络。在弱关系网络中，由于不同社团间的联系较弱，使得不同粒层中粒的粒度差异较小，而对于强关系网络，由于社团内部边的密度与不同社团间的边密度差异较小，使得小社团快速合并成大社团，导致不同粒层间的粒度差异会非常大。在强关系网络中，随着粒化层数的增加，各粒层中相应粒的特征趋于雷同，若拼接过多类似的特征将导致节点自身的特征被弱化，导致Multi-GS 的性能会有先提升再降低的情况。因此，针对不同的数据集，如何设置一个合理的粒化层数是Multi-GS 需要考虑的问题。

3.3 链接预测

链接预测任务是预测网络中给定节点间是否存在边。通过链接预测可以显示不同网络表示方法的链接预测能力。对于链接预测任务，仍然选择Citeseer、PPI、WiKi 和BlogCatalog 作为验证数据集，分别从不同数据集中随机移除现有链接的50%。使用剩余网络，利用不同的方法学习节点表示。另外，将被移除边中的节点对作为正样本，同时随机采样相同数量未连接的节点对作为负样本，使正样本和负样本构成平衡数据集。实验中，首先基于给定样本中的节点对，通过表示向量计算其余弦相似度得分，然后使用Logistic 回归分类器进行分类，并通过曲线下面积[29](area under curve，AUC)评估标签间的一致性和样本的相似性得分。对于Multi-GS，k为0～4。表6显示链接预测任务中，不同算法在Citeseer、PPI、WiKi 和BlogCatalog 数据集上的AUC 值，其中，粗体表示性能最好的结果，下划线表示对比算法中性能最优的结果。

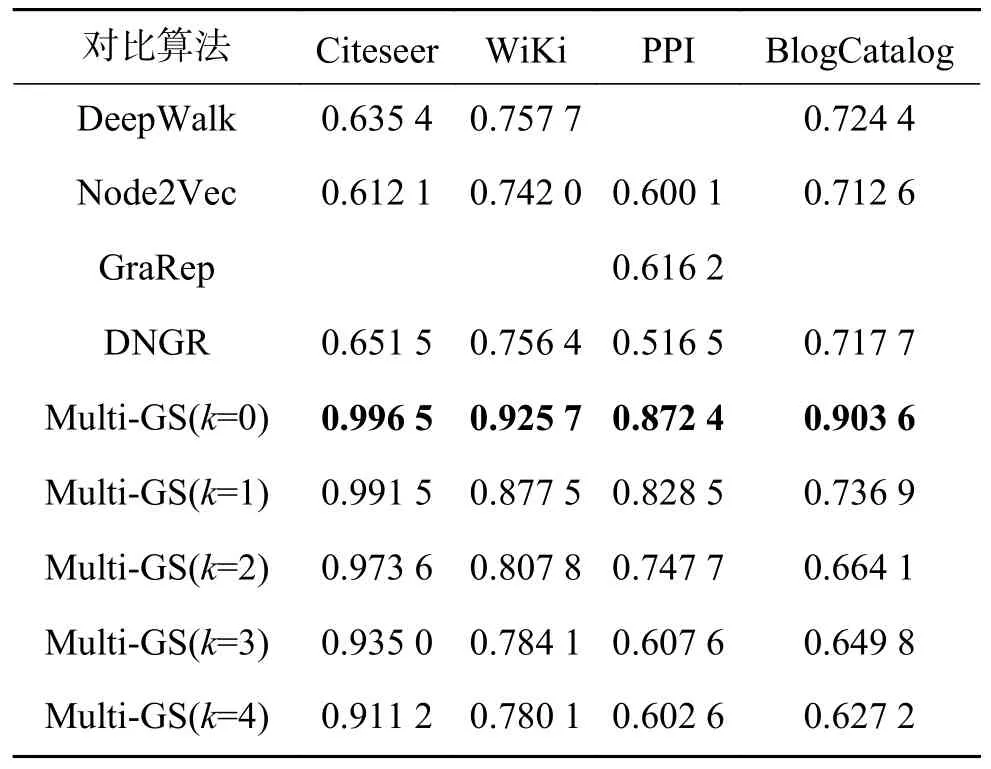
表6 链接预测任务中不同数据集上的AUC 结果Table 6 AUC score on all datasets

表6 的结果显示，在对比算法中，GraRep 表现依然最好。对于Multi-GS，当不使用联合学习框架时，方法的性能是最优的。以AUC 为评价标准，相对于对比算法中的最优结果，在Citeseer 数据集上相对提高45.24%，在WiKi 数据集上相对提高15.4%，在PPI 数据集上相对提高39.14%，在BlogCatalog 数据集上相对提高20.66%。但是，随着粒化层数的增加，对于链接预测任务，方法的性能会越来越差，下降速度会随着网络的密度成正比。综合来看，在链接预测任务中，利用多粒度结构联合学习到的节点表示无法提升链接预测能力，说明该类任务需要更多节点自身的特征，节点低阶相似性比高阶相似性更重要。虽然融合多粒度结构中节点的高阶特征会导致Multi-GS 性能下降，但可以看出，在较低的k值下，仅利用节点的拓扑结构信息，Multi-GS 的链接预测结果十分理想，说明Multi-GS 中GCN 模型能有效地捕获节点的低阶相似性。

3.4 可视化

在本小节中，对Multi-GS 和对比算法学习的节点表示利用可视化进行比较。由于空间限制，实验选择节点数较少的Cora 作为可视化数据集。其中，每个节点代表一篇机器学习论文，所有节点按照论文的主题分为7 类。实验通过t-SNE[27]工具，将所有方法的节点表示投影到二维空间中，不同类别的节点用不同的颜色显示。可视化结果如图4 所示。

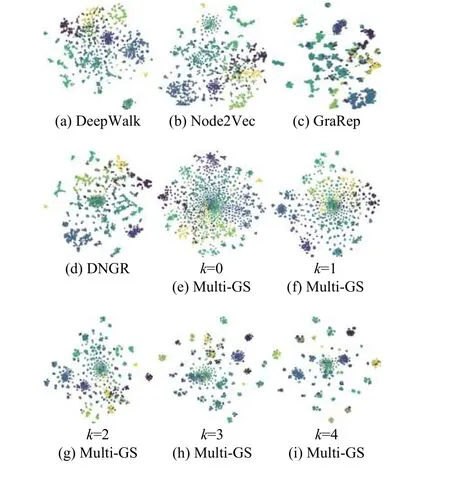
图4 Cora 数据集的可视化结果Fig.4 The visualization of Cora dataset

在图4 中，DeepWalk、Node2Vec 的表示结果较差，节点散布在整个空间中，不同类别的节点相互混在一起，无法观察到分组结构，意味着算法无法将相似节点组合在一起。通过GreRap 的可视化结果，能够看出节点间的分组结构。对于Multi-GS，在图4(e) 中，不同分类的节点相互混合，这种现象在图的中心尤其明显。意味着仅保留低阶相似性的节点表示无法区分不同分类的节点。图4(f)显示结果与图4(e)相似。在图4(g)～图4(i)中，可以看到节点逐渐开始呈现紧凑的分组结构，而且不同组之间的距离越来越大，随着层数的增加，Multi-GS 可以将相似结构的节点进行分组并推到一起。因此，在节点分类任务中，利用多粒度结构使Multi-GS 获得更好的结果。

3.5 参数敏感性分析

本节进行参数敏感性实验，主要分析不同的特征维度和粒化层数对Multi-GS 性能的影响。实验针对Citeseer 数据集，利用Multi-GS 在不同粒化层数下学习到的不同维度的节点表示，通过节点分类、节点聚类和链接预测任务对Multi-GS 进行评估，并报告相关的实验结果。对于节点分类任务，随机选择50%节点训练分类器。采用Micro-F1 和Macro-F1 作为评价指标。对于节点聚类任务，采用NMI[30]和ARI[30]作为评价指标。对于链接预测任务，移除50% 的链接，采用AUC 作为评价指标。参数k表示最终节点的特征表示融合的粒化层数，若k=0，表示仅选取最细粒度的粒特征表示作为最终的节点特征表示，k=1，表示用第0 层和第1 层的粒学习到的特征表示进行拼接后的向量作为最终的节点特征表示，以此类推。其中，0 表示最细粒度，k值越大，表示粒度越粗。对于所有任务，重复实验10 次并报告平均结果，实验结果如图5 所示。

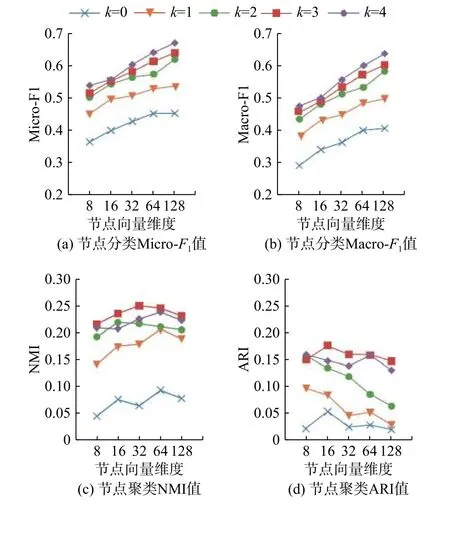
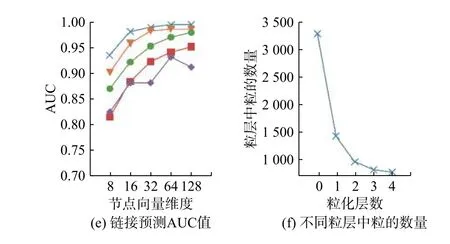
图5 参数敏感性分析Fig.5 Parametric sensitivity analysis

图5 的结果表明，对于节点分类任务，Micro-F1 和Macro-F1 指标随着特征维度的上升而上升。因为一个更大的特征维度可以保留网络中更多的信息。随着粒化层数的增加，Micro-F1 和Macro-F1 指标也逐渐提升，但是可以看出，这样的提升效果会随着粒化层数的增加而越变越小，甚至退化。对于节点聚类任务，NMI 和ARI 的最优结果都出现在k=3 时，继续增加层数，结果会下降。对于链接预测任务，AUC 指标随着特征维度的上升而上升，这是合理的情形。但是当k=4 时，AUC 指标发生波动，说明叠加更多的层次会导致学习的特征表示发生信息变化，这是需要避免的情况。通过图5(f)中显示的各层中粒的数量的变化曲线，可以看出，不同层间的粒度差异会随着层数的增加而减少。在第3 层和第4 层间，这种粒度差异几乎很小，意味着节点在第3 层和第4 层中的特征极为相似，若拼接过多类似的高阶特征向量，导致节点自身的特征被弱化，使得最终Multi-GS 的输出表示不能在网络分析任务中发挥出方法优势。

4 结束语

在网络表示学习中，如何让学习到的节点特征表示能够保留网络结构的局部和全局特征，仍是一个开放和重要的研究课题。本文结合分层递阶的思想，提出一种无监督网络表示学习方法Multi-GS，通过构建网络的深度结构解决GCN 无法有效捕获节点高阶相似性特征的问题。该方法首先利用模块度增量逐步构建网络的多粒度分层结构，然后利用GCN 模型学习不同粒度空间中粒的特征表示，最后将已学习的粒特征向量逐层映射拼接为原始网络的节点表示。利用Multi-GS 可捕获多种网络结构信息，包括一阶和二阶相似性、社团内相似性(高阶结构)和社团间相似性(全局结构)。

为验证Multi-GS 方法的性能，通过在4 个真实数据集上进行节点分类任务和链接预测任务，并与几个经典的网络表示学习方法进行比较。从实验结果上看，针对节点分类任务，使用多粒度结构的Multi-GS 能够改进节点的特征表示，提升GCN 模型的节点分类性能。但是由于网络结构的多样性和复杂性，Multi-GS 的粒化层数无法固定，必须根据不同结构的网络进行调整。针对链接预测任务，使用多粒度结构M u l t i-G S 对GCN 模型的性能造成损害。说明节点间的低阶邻近关系对链接预测任务是至关重要的。尽管如此，在不使用多粒度结构的情况下，以AUC 为评价指标，相对于对比算法，Multi-GS 的性能优势非常明显。针对Multi-GS 超参数敏感性的实验结果可以看出，面对不同的网络分析任务，融合不同粒度的粒特征对Multi-GS 的性能有着不同程度的影响。

未来工作方向包括探索其他网络粒化分层技术和继续深入研究不同的层和不同粗细的粒以及不同类型的网络结构对Multi-GS 的影响。