磨床冷却系统的可靠性建模及评估研究∗∗
刘 超 白 强 马庆锋 杨振林 战智涛
(齐鲁工业大学(山东省科学院)山东省科学院海洋仪器仪表研究所,山东青岛266061)
随着现代制造业的高速发展,对数控磨床的要求也越来越高。数控磨床作为集机、电、液、光于一体的现代化制造装备,主要应用于航空、航天、汽车等高精密工件的加工上,由于本身集成的复杂性,就会对其可靠性提出较高的要求。对比国外进口的数控磨床,国产的数控磨床在可靠性方面还存在很大的差距。因此,加快数控磨床可靠性提升工程已尤为重要。国内外学者对数控机床可靠性方面做了大量的研究工作。俄罗斯的研究人员对产品的可靠性提升的具体措施作了研究[1]。Kerr等人用计算机图像处理技术对机床的刀具磨损进行了在线监测,评估了刀具剩余寿命[2]。日本新潟大学的藤井义对加工中心进行现场跟踪试验,并对加工中心进行故障分析,对其可靠性指标进行了评估[3]。申桂香等通过赋权的方法对数控机床的可靠性进行评价[4],廖雯竹等针对设备可靠性随使用年限以及维修次数的增加而降低情况,建立了基于设备可靠性的顺序预防性维护优化模型,引入威布尔分布对某列车检修设备进行仿真分析[5]。大部分都是对整机进行可靠性评估,对数控磨床子系统进行研究的比较少,所以对数控磨床子系统进行可靠性评估显得尤为重要。
1 故障数据预处理及散点图的绘制
对于故障数据的采集和预处理有多种方式[6-7]。绘制故障时间分布函数以及概率密度函数的散点图,可以使用等时间频次法以及经验分布函数法。使用两种方法对故障时间进行处理,可以较好地减小误差,在进行综合分析后进行数据拟合,可以减小拟合的范围,减小工作量。
1.1 等时间频次法
使用等时间频次法是为确定时间区间的大小,时间区间的大小决定出现故障时间频次的多少,进而影响区间内散点的多少,使得获得概率密度图不够精确。可以根据经验公式来获得分组从而确定时间区间大小。区间分组的经验公式为:

式中:nf是数组中故障数据的个数;K为分组数。
利用获得的分组数进行分组,获得故障间隔时间分组表,如表1所示。

表1 故障间隔时间分组表
表1中:tmax是故障数据采集获得的最大时间值;k为分组数;ti-是分组区间的左端点;ti+是分组区间的右端点;是分组区间的中间值;ni是第i组内故障个数;fi是第i组内故障发生的频率;为概率密度观测值。的计算公式为:

式中:ni为每组故障间隔工作实践中的故障频数;n为故障总数;Δti为组距。
1.2 经验分布函数法
用经验分布函数法将故障数据处理,将故障间隔时间按照大小顺序排列:t1≤t2≤…≤tn,为减小误差,常用中位秩近似计算F( ti):

式中:i为故障数据的标号(1,2,…,n);n为故障数据的总数。利用故障间隔时间ti作横坐标,F ti()为纵坐标,绘制故障间隔时间分布函数的散点图。
2 参数估计
通过对故障间隔时间分布密度函数散点图以及故障间隔时间分布函数散点图的绘制,可以初步确定分布函数所属类型,进而使用最小二乘法[8]对所属分布中的参数进行估计。基本思路就是将非线性问题转化为线性问题,从而求出未知量。基本步骤:
假设有n个观测值 (xi,yi)(i= 1,2,…,n),如果x、y之间存在线性关系,即可以用直线来拟合x、y之间的关系。

其中,参数a,b的值为:

2.1 威布尔分布的参数估计
威布尔分布的函数表达式:

对于威布尔分布[9]可以将两边取自然对数,然后化简可以得到,时间t如果服从威布尔分布,则{ln t,lnln[ 1/(1-F( t))]}服从线性关系,进而利用x=ln t,y=lnln[ 1/(1-F( t))]构造线性关系式:

从而求出未知量m、η。
2.2 指数分布的参数估计
指数分布的函数表达式:

也可以采用威布尔分布进行参数估计的方法,进而可以获得{t,ln[1-F t()]}服从线性关系,可以利用x=t,y=ln[1-F t()]构造线性关系式:

从而求出未知量λ。
3 分布函数的拟合检验
在初步假设函数的分布类型后,需要对所属分布进行检验,已确定假设的分布函数为正确的。这里使用χ2检验的方法,这种方法的基本原理是在于比较出理论频数与实际频数之间的差异,然后将用来接受检验的统计量χ2的观测值与标准临界值之间进行比较,来检验假设分布是否正确。
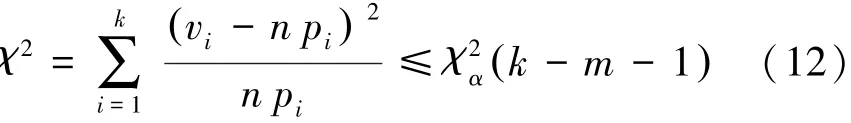
式中:n是样本数量;k是分组数;m是未知参数的个数;α是显著性水平;vi是第i分组的实际频数;pi是第i分组理论频率。
4 分布模型优选
根据假设检验过程,可能出现假设的几种分布都正确的情况,对于哪一种分布更加符合实际的分布情况,这就需要对模型进行优选。经过了拟合检验,一般使用拟合优度值的比较来确定分布函数最终的选择。拟合优度[10]一般使用R表示:

式中:yi是拟合值;是yi的平均值;是观测值。
通过优度值的计算比较,就可以判断函数所属的分布类型,进而进行可靠性评估指标的计算,获得相应的数值。
5 数控磨床冷却系统可靠性指标计算实例
5.1 散点图的绘制
现在将为期一年半的6台MKS系列数控磨床的故障数据进行分类整理,获得数控磨床冷却系统故障数据27个。根据公式(1)计算得到分组 K=1+3.322log27=5.75,这里可以取6。数据采集采用定时截尾法,采集区间的最大时间值为14 664 h获得故障间隔时间分组表,如表2所示。
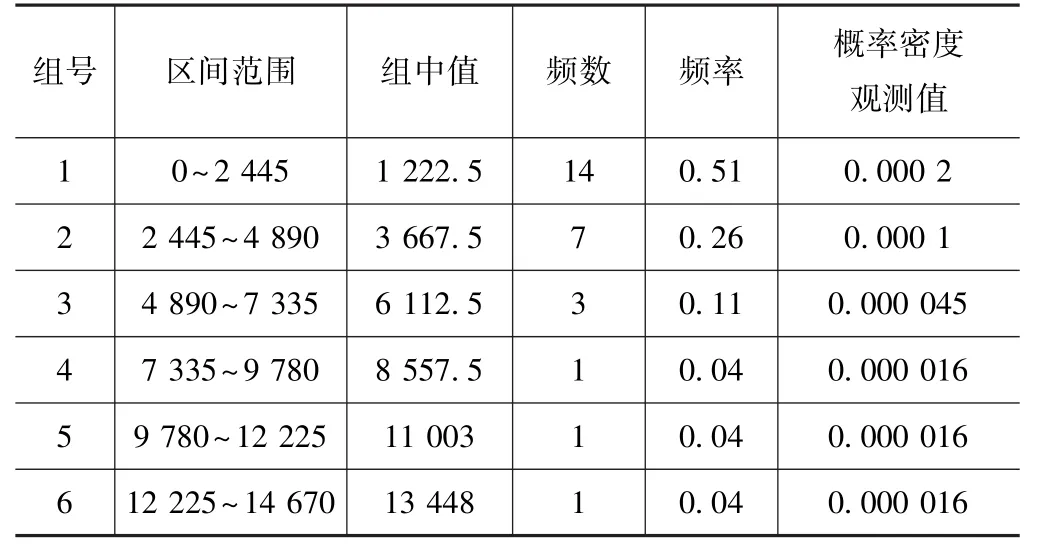
组号 区间范围 组中值 频数 频率 概率密度观测值1 0~2 445 1 222.5 14 0.51 0.000 2 2 2 445~4 890 3 667.5 7 0.26 0.000 1 3 4 890~7 335 6 112.5 3 0.11 0.000 045 4 7 335~9 780 8 557.5 1 0.04 0.000 016 5 9 780~12 225 11 003 1 0.04 0.000 016 6 12 225~14 670 13 448 1 0.04 0.000 016
利用表2的组中值以及概率密度观测值作故障间隔时间分布密度函数散点图,如图1所示。
利用故障间隔时间ti作横坐标,F ti()为纵坐标,绘制故障间隔时间分布函数的散点图,如图2所示。


根据图1和图2可以假设分布函数属于威布尔分布或者指数分布。
5.2 分布函数的参数估计
根据公式(8)和(9)计算出 m=0.012 3,η=596.530 3。分布函数属于威布尔分布时的公式为:
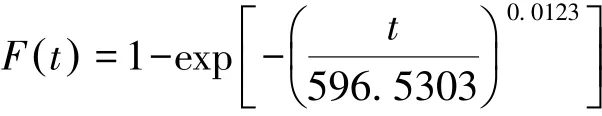
根据公式(10)和(11)计算出λ=0.000 3。因此分布函数属于指数分布时的公式为:
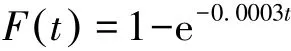
5.3 分布函数的拟合检验
使用χ2检验法检验两种分布是否符合假设。利用公式(12)分别计算出威布尔分布和指数分布时的χ2值,与标准值进行比较。
(1)威布尔分布的拟合检验
威布尔分布函数的表达式为:

其函数拟合图,如图3所示。
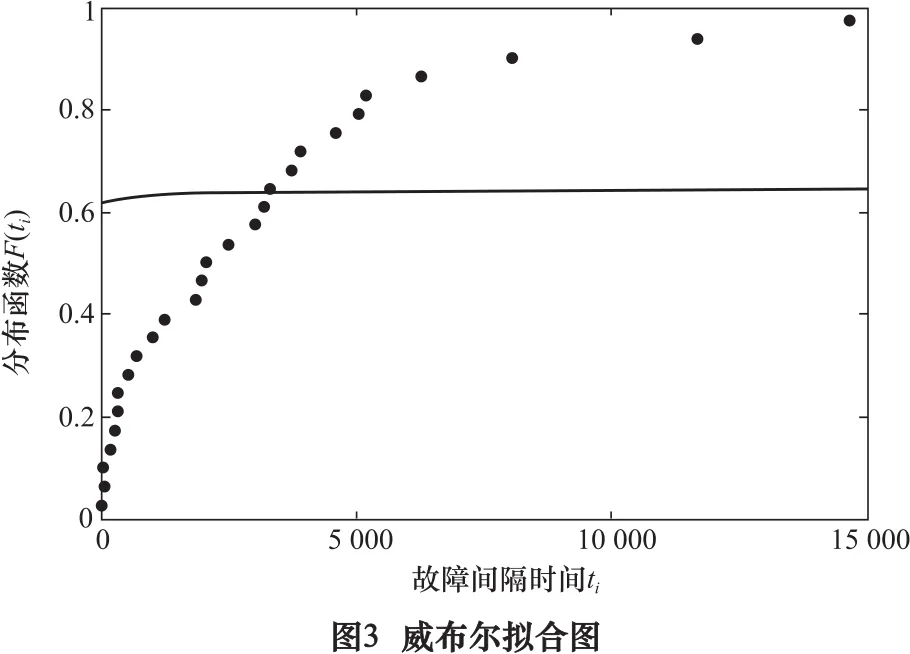
(2)指数分布的拟合检验
指数分布函数表达式为:

其函数拟合图,如下图4所示。

由此可见威布尔分布并不符合假设,假设不成立。指数分布属于符合假设。因而可以得到故障间隔时间分布属于指数分布。
5.4 可靠性指标的计算
根据上述计算得到的数控磨床冷却系统的分布可以进行相关的可靠性指标计算[11-14],可以得到数控磨床冷却系统的故障间隔时间符合指数分布,且指数分布的表达式为:

(1)平均故障间隔时间
平均故障间隔时间(MTBF)是指在设备发生一次故障到下一次故障间的平均工作时间。在已知设备故障间隔时间分布概率密度函数f t()的情况下,平均故障间隔时间MTBF:
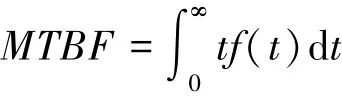
由于故障间隔时间分布符合指数分布,且表达式为F t()=1-e-0.0003t,因此可以得到故障间隔时间分布概率密度函数f(t)的表达式为:

进而计算冷却系统的平均故障间隔时间(MTBF):

(2)平均维修时间
平均维修时间(MTTR)是指从故障到维修完成所用时间的平均值。

式中:N是测试的产品总数;ni是第i个测试产品的维修次数;τij是第i个产品从第j次维修所用的时间。

(3)固有可用度
数控磨床的可用性水平是反映设备能工作时间以及设备服务时间之间的比值,是可靠性与维修性的综合反映。固有可用度A是指在规定的使用条件下,数控磨床保持其规定功能的概率:

由此可见数控磨床冷却系统的可用性比较高,有效工作程度较高,具有较好的综合功用。
6 结语
通过对工厂采集到的故障数据进行分析,对数控磨床的子系统——冷却系统进行了详细分析与指标评估。对数控磨床冷却系统的故障间隔时间进行分组,绘制其分布函数散点图以及分布密度函数散点图,利用参数估计和分布检验计算并确定故障间隔时间的分布为指数分布,并且得到分布函数表达式。利用分布函数的表达式分别计算了数控磨床冷却系统的平均故障间隔时间MTBF为3 333.33 h,平均维修时间MTTR为1.26 h以及固有可用度A为0.999 6。以上计算的结果已经反馈到生产厂家得到了认可,并应用到后续可靠性提升的工程当中。

