反褶积数据处理方法在特低渗透储层试井解释中的应用

郭金城

(中国石化胜利油田分公司勘探开发研究院)

新疆某油田M2井区为深层特低渗透性油藏，统计M2井区17井次压力恢复或降落资料，10井次油井中仅2口井勉强出现了平面径向流，而7口注水井均没有出现径平面向流，严重影响了流动边界的识别和资料的充分利用。由于不能无限制地进行压力恢复试井，因此有必要研究适合于新疆油田M2井区的试井资料解释方法。

不出现径向流直线段资料的试井解释一直是试井领域的难题[1-2],国内外学者做过不少研究，具有代表性的方法有褶积、反褶积法、井筒储集反卷积法和改进方法等[3-4],其中反褶积法是试井专家一直致力研究的问题,但却因算法稳定性问题一直未能有效应用。直到Schroeter等人解决了反褶积技术上算法稳定性问题[5]，反褶积方法才引起试井界同行的广泛关注。刘能强[6]指出反褶积方法只不过是个非线性的最优化过程，仍旧具有一定的局限性，任何误差都将积累并影响随后的整个过程。李爱清等[7-14]通过Schroeter反褶积方法成功的获取了目标井数据处理，获得了地层流动特征及参数信息，可见国内采用反褶积方法进行特低渗透储层试井资料处理解释的人很少。本文结合反褶积方法原理，论述了反褶积方法的适用条件和应用注意事项，应用反褶积方法处理M2井区部分测试井原始数据，获得了较好的解释效果。

一、反褶积方法原理

如果函数f(t)和g(t)满足：

f(t)=g(t)=0

而反褶积是由产量史q(t)及压力响应Δp(t)求解重整压力Δpu(t)的过程，在数学上是个反问题、存在多解性。根据杜哈美原理，得到研究压力降落和压力恢复的褶积方程为:

(1)

Δp=pi-pwf(t)

(2)

式中:pwf(t)—生产t时刻井底压力，MPa；

t—生产时间，h；

q—井的产量，m3/d；

pi—原始地层压力，MPa；

Δpu—重整压力，MPa。

反褶积在试井解释中的应用是40多年来许多试井解释专家们所思考和研究的课题，但由于计算方法上的稳定性问题一直没有解决，使人们认为反褶积是一个好方法，但在试井解释中却无法使用。根据Schroeter，Hollaender和Gringarten[15]等人的研究方法，定义了两个新变量：

σ=lnΔt

(3)

(4)

实际上σ和ez(σ)是压力导数曲线上的两个坐标，则式(2)中Δp可以变为：

(5)

由于构成褶积的两个函数q(t-eσ) 和ez(σ)都是复合函数，而且公式(5)中Δp为非线性方程。那么反褶积试井方法就是利用式(5)和最优化方法找出一个线性分段函数z(σ) ，应用最优化方法将褶积模型和实测压力数据、压力导数曲线总曲率、产量拟合误差优化至最小。得到反褶积结果后通过积分转换为压力响应，得到恒定产量下的反褶积试井曲线，最后应用恒定产量下的压力恢复(降落)模型进行拟合解释。反褶积拟合的准确程度依靠对试井解释结果达到的历史拟合率来判断，如果达到了满意的实际压力历史拟合率，则可以认为反者积的拟合误差是最小的，结果是可靠的。

二、反褶积的应用条件

1.反褶积的应用条件

线性条件对于反褶积方程尤为重要，流动方程和边界条件都有可能发生非线性现象。流动方程的非线性包括储层岩石和流体物性的压敏性以及多相流动。对于低于露点压力的反凝析气藏、低于泡点压力生产的油藏、变流体饱和度的水区储层情形，方程的非线性尤为重要。边界条件的非线性包括：变井筒储存效应，如相态分离或与压力相关的井筒储存效应；变表皮系数，如非达西流动、洗井、增产措施、表皮系数随生产时间降低等情形；边界条件，如临井损害，下倾水体引起的水侵等。

2.反褶积的应用建议

由于反褶积具有不稳定和多解性应用时应多加小心，Levitan等[16]给出了几条改进反褶积分析结果的建议：

(1)利用压力恢复数据进行反褶积分析。与生产阶段数据相比压力恢复数据品质较高。

(2)产量、压力数据同步。对于常规分析同步过程中产量与压力少量的数据不匹配仅局部影响分析结果；对于反褶积分析则可能改变整个测试阶段的反褶积压力响应形状。

(3)除去非线性现象造成的失真数据。

(4)利用全部产量史数据。建议：至少2倍于压力恢复时间之前的生产史，才可用基于实际生产时间的平均产量代替。对于探井来说，特别是出现线性流情形时，最好选用全部产量史而不是选用Levitan推荐的2倍关井时间的建议。

(5)分别开展历次压力恢复反褶积。历次压力恢复反褶积分析应该给出相同的反褶积压力响应。反褶积压力响应之间的任何差异，都应该在反褶积结果确认之前进行一致性检验。

(6)通过调整原始压力，实现历次压力恢复分析结果一致。反褶积分析结果对原始压力非常敏感。

三、实例分析

A井是M2井区的一口生产井，选择该井生产历史中关井时间相对比较长的三个恢复段进行分析，其中第一段关井144 h，第二段关井329 h，第三段关井118 h。

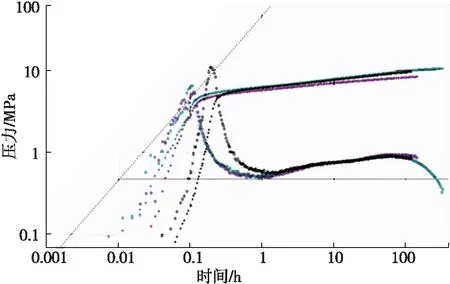
图1 A井三次压力恢复段的双对数曲线图

图1中紫色曲线为第1段、蓝色曲线为第2段、黑色曲线为第3段，可看出三次压力恢复曲线都没有完全反应出该井的泄流区域地层信息。其中，依据第一段或第二段曲线特征可判断为复合非均质渗流、均质+多条断层的渗流、也可以是双孔介质+边界的渗流，依据第三段曲线特征可判断为均质+封闭系统的渗流、复合非均质+封闭系统的渗流、双孔介质+封闭系统的渗流，但无法确定封闭系统的形状。可见测试时间不同反应出的地层信息也不同，即使关井时间最长的第二段也难以说明该井泄流范围的真实情况。

为此，采用了反褶积方法处理了产量压力数据，应用重整压力数据绘制了图2双对数曲线图，可判断为测试井处于均质油藏矩形边界封闭系统一角的流动模型。该井最终解释结果：地层初始压力67.61 MPa、地层系数3.9 mD·m、地层渗透率0.427 mD、表皮系数-1.24，矩形边界分别为31.4、31.4、140、200 m，目前地层平均压力40.55 MPa，对应三个压力恢复段时期的平均地层压力分别是65.55、52.63、47.57 MPa，可见地层压力下降很快，A井确实处于一个有限的封闭系统中。仅用常规压力恢复数据解释得到的平行封闭边界模型不能准确解释原始地层压力，结果明显偏低(见表1)。

图2 AH01井反褶积处理的双对数曲线图

注：1Psi=6.894 kPa。

表1 A井不同试井方法下试井解释结果对比表

对比图1、图2可知反褶积处理后的压力数据时间明显高于正常压力恢复测试时间，因此反褶积数据处理的实质相当于延长了测试时间。关井时间总是有限的，但生产历史却可以很长，重整压力双对数曲线有利于全面认识封闭系统形状与距离关系，反映的泄流范围内地层信息更多，从而提高了试井解释准确度。这也说明流动压力监测与静压力监测同样重要，足够长时间的流动压力监测有利于反褶积数据处理，可以获得更准确的试井解释结果。

B井是M2井区的一口提捞生产井，周围没有注水井注水，处于完全弹性生产阶段，对其试采阶段的测试数据进行了解释分析。

B井试采半年后进行关井测试，压力产量历史见图3，其压力恢复双对数曲线如图4。从图4可知，该井可以用均质油藏+边界模型进行解释，也可以用复合非均质模型进行解释，但无法确定究竟是什么模型。压力产量数据经过反褶积处理后，应用重整压力绘制了图5所示的双对数曲线图，该曲线准确无误地显示地层为复合非均质油藏模型，双对数曲线后期出现了平面径向流特征。对比图4、图5的双对数曲线的时间轴也可以发现，反褶积得出的双对数曲线时间明显大于常规压力恢复试井解释的双对数时间，这正是反褶积能够取得径向流特征的主要原因。因此同常规试井解释相比，压力反褶积方法获取的重整压力双对数曲线反应的测试半径更大，获取平面径向流动的特征可能更大，解释结果可信度更高。

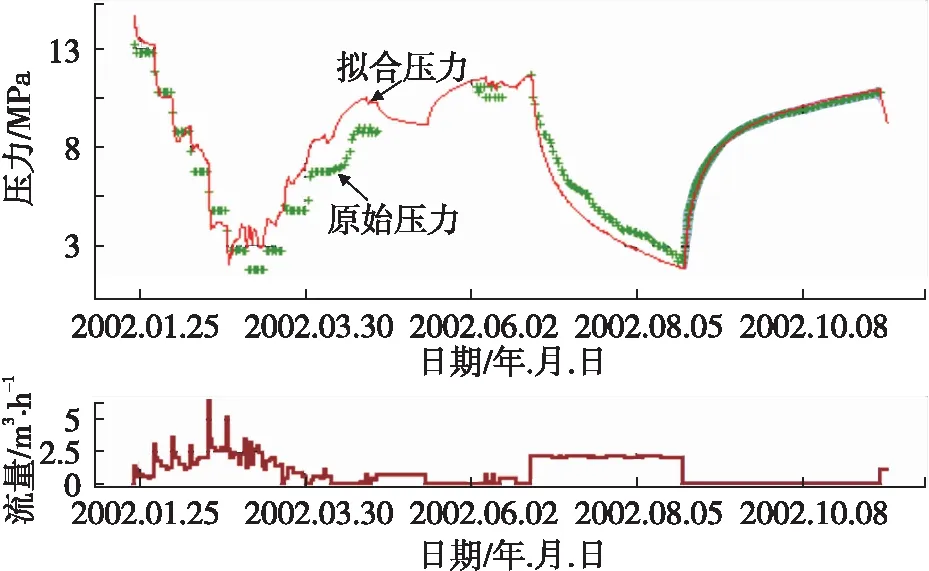
图3 B井压力和产量历史曲线图

从上述两例可见，低渗透或特低渗透储层压力恢复试井的压力数据经过反褶积数据处理后，能够识别出油藏边界流动特征，容易获得平面径向流动阶段，解释的资料更加准确，是解决目前低渗透或特低渗透储层试井解释的有效手段。

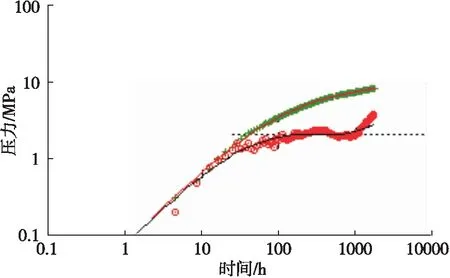
图4 B井压力恢复双对数曲线图

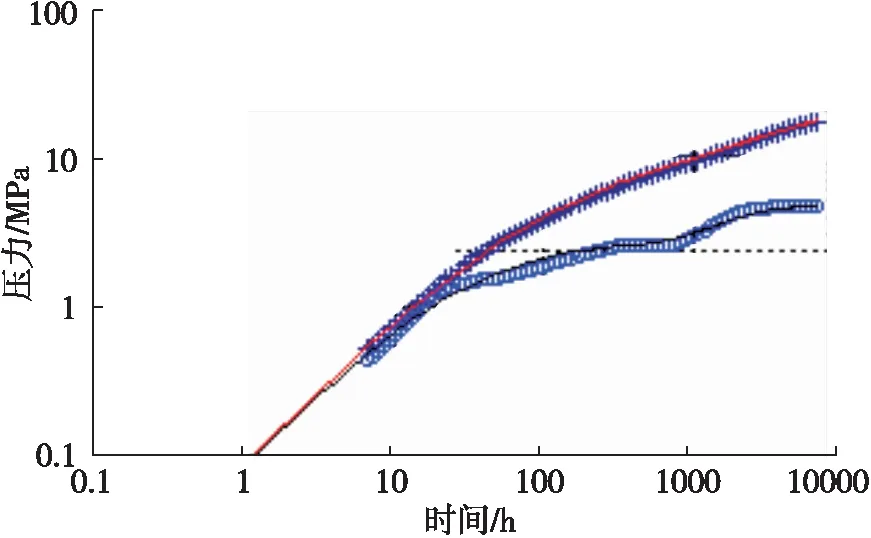
图5 B井反褶积处理的双对数曲线图

四、结论

(1)对于低渗透油藏试井分析来说压力反褶积处理方法相当于延长了测试时间，依靠重整压力绘制的时间压力双对数曲线图能够识别出油藏的流动边界特征，一定程度上克服了常规试井解释无法获取低渗透储层流动边界特征的问题。依据重整压力绘制的时间压力双对数曲线图容易出现平面径向流阶段，使得解释的地层参数信息更为准确。

(2)低渗透油藏试井时应注意流动压力的测试时间，流动压力测试时间足够长是获得足够长时间的重整压力恢复曲线的基础。

(3)反褶积数据处理时要充分考虑反褶积的线性条件，注意非线性现象及异常数据的剔除。