基于多层编码遗传算法的舰艇改造任务分配方法∗

李一夫 宋贵宝 贾汝娜 张文鹏

（1.海军航空大学 烟台 264001）（2.国防大学联合勤务学院研究生管理大队 北京 100039）

1 引言

由于我国海域范围辽阔且近年来海洋维权执法任务繁重，提高我国海监渔政执法力量对有效管理海洋秩序、合理利用海洋资源、坚定维护海洋权益等方面具有现实意义。海军舰艇退役以后，拆卸军舰的重型武器系统、改装新设备并移交海洋执法部门一直都是世界各国的惯例。本文将多层编码的遗传算法作为工具，寻找最短时间改造退役军舰的任务分配方案，可以在兼顾执法船只整体吨位、续航能力、功能等有效执法能力的同时，及时缓解执行海洋维权船只不足的问题，最大限度地再利用退役军舰的剩余价值。

2 问题描述

对退役军舰的改造问题根本上是根据任务要求合理分配改造工序和船坞，从而提高改造作业过程效率的项目管理问题［1］。从数学的角度可以描述为：有n艘待改造的舰艇要在m个性能不同的船坞内进行改造，每艘舰艇需要经历q道工序，每艘舰艇的各工序可在不同船坞内完成改造，最终寻求最短时间内全部舰艇完成全部工序改造的优化方案。此外，改造过程中还应满足以下假设：

1）同一时刻每个船坞只能进行一艘舰艇一道工序的改造；

2）每道工序只能在同一个船坞内完成且中途不可停工；

3）工序存在优先级，但待改造舰艇和船坞无优先级［2～5］。

3 确定工序优先级

改造任务从系统工程的角度出发，工序存在排序问题。由于不同工序间相互关联，改造先后顺序直接影响改造流程的正常运行，例如在加装新设备之前应先拆除原军用设备、重设电气系统等。从系统化、层次化的角度出发，运用定性与定量相结合的方法——层次分析法［1］确定合理的工序优先级可以较好体现项目管理的系统属性。

4 模型建立

4.1 模型参数

1）待改造舰艇集 P=｛p1，p2，p3，…，pi，…，pn｝，pi表示第i艘待改造舰艇，i=1，2，3，…，n。

2）船坞集 M=｛m1，m2，m3，…，ms，…，mm｝，mj表示第j个船坞，j=1，2，3，…，m。

3）工序序列集 OP=｛op1，op2，op3，…，opq｝。

4）可选船坞 OPM=｛opi1，opi2，opi3，…，opik｝，opij=｛opij1，opij2，opij3，…，opijk｝表示舰艇 pi的工序 j可以选择的加工机器。

5）改造舰艇的时间矩阵T，tij∈T，表示第i艘舰艇pi改造第j道工序的时间。

6）Aij为第 i艘舰艇开始第 j道工序的时刻，Eij为第i艘舰艇完成第j道工序的时刻。

7）工序间等待时间之和为λ。

4.2 优化模型

工序确定。运用层次分析法确定各工序的优先级，并按优先级由大至小的顺序分别对应工序集OP中第一至最后一个元素，即op1优先级最高，op2次之，opq优先级最低。

目标函数。本文目标是使加工所有舰艇所有工序的时间与工序间等待时间λ之和最小。

约束条件。同一时刻一艘舰艇只能在一个船坞内进行改造；同一时刻一个船坞只能改造一艘舰艇；且后一道工序必须在前一道工序完成后才可进行。因此得到如下数学模型：

其中，nis表示某时刻s船坞内第i艘舰艇的数量；nij表示某时刻i舰艇在第j个船坞内的数量；Eij表示第i艘舰艇完成第 j道工序的结束时刻；Ai（j+1）表示第 i艘舰艇开始第（j+1）道工序的开始时刻；自变量x为优化后的任务分配方案并最终可形成任务安排甘特图，从而方便使用。

5 基于多层编码遗传算法求解过程及实现

5.1 算法流程

首先进行种群初始化，确定初始解集，按整数编码的方式对染色体进行多层编码，；计算适应度值；利用轮盘赌方法对个体寻优；利用整数交叉法产生新的个体；利用整数变异法得到变异后的优秀个体；进行判别选择循环或者结束［6］。

5.2 算法实现

1）个体编码

每个染色体按照整数编码的方式反映一个可行解的二维特征，即工序和所选机器型号。待改造的舰艇总数为n，舰艇ni改造工序为mj时，则每个染色体的长度为

其中染色体的前半部分表示为所有舰艇的改造顺序，后半部分表示为舰艇每道工序选择的船坞序号。例如个体｛16543321//29885321｝“//”前后各有2个数组，各位置一一对应。“//”前面的数表示所有舰艇的改造顺序，“//”后面的数表示舰艇的每道工序被处理的船坞序号。第一层编码描述的改造顺序为舰艇1→舰艇6→舰艇5→舰艇4→舰艇3→舰艇3→舰艇2→舰艇1；第二层编码描述的船坞依次为船坞2→船坞9→船坞8→船坞8→船坞5→船坞3→船坞2→船坞1。

2）计算适应度

染色体的适应度为全部舰艇改造完成的总时间，公式为

其中time指全部改造任务完成时间，time越小该染色体越优秀［7～8］。

3）选择操作

采用轮盘赌法选择适应度较好（适应度值大）的染色体［4］，个体选择概率为

其中pi（i）表示染色体i在每次选择中被选中的概率。

4）交叉操作

交叉操作创造出的新染色体是推动种群进化的主要因素。交叉操作首先随机选择两个染色体，在每个染色体的前位随机选择交叉位置进行交叉操作［9～11］。

5）变异操作

变异操作获得的新的个体是推动种群进化另一个因素。首先利用变异算子从种群中随机选取变异个体，然后选择变异位置S1和S2，最后把个体中S1和S2位的工序和对应的船坞序号交换位置［12］。

6 算例仿真实现

算例可描述为6艘待改造舰艇，在10个船坞内进行改造，除必须首先完成的“拆除军用武器设备”这一道工序以外，每艘舰艇还需要经历5道工序，即总共6道工序。试寻找在最短时间内完成所有舰艇改造的优化方案。

首先确定工序的优先级。“拆除军用武器设备”作为固定的第一道工序，其优先级最大，故只需要比较剩余五道工序。比较是两两工序之间进行的比较，根据比较尺度表（见表1）请专家对两两工序的重要程度打分。用aij表示第i道工序相对于第j道工序的比较结果，得到比较矩阵A=（aij）。

该比较矩阵A的最大特征值λ=5.073，归一化特征向量为Ω=［0.263，0.475，0.055，0.099，0.110］。为了判断五个工序优先级比较结果是否具有一致性，计算总排序一致性比率进行检验。

故A通过一致性检验。按优先级由大至小的顺序分别命名工序为工序2至工序6。

然后，利用多层编码遗传算法寻找最优任务分配。利用Matlab 2014a环境中谢菲尔德大学遗传算法工具箱，按照上文建立的数学模型及多层编码遗传算法编程并进行模拟仿真实验，形成优化方案。每个工序可选择的船坞编号如表2所示，每道工序在对应船坞内的改造时间如表3所示。

表2 工序可选船坞表

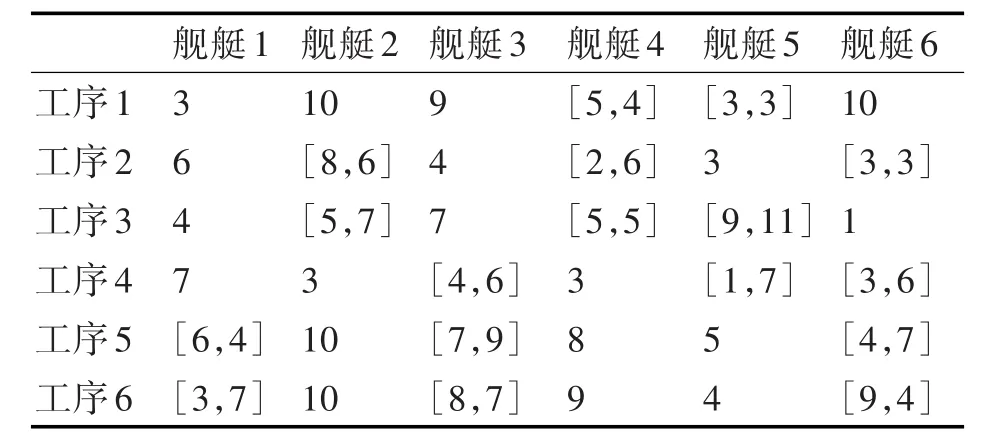
表3 工序改造时间

各参数分别设为种群数量为40，最大遗传代数为50，交叉率0.8，代沟0.9，变异率0.6。算法搜索得到最优方案的完成时间为49，算法过程和反映最优优化方案的甘特图分别如图1和图2所示。

7 结语

本文主要讨论了退役舰艇改造任务分配问题。针对工序多、船坞多、舰艇多的任务特点选择多层编码遗传算法筛选出最优方案，算法经验证能得到稳定解，效果良好，可以较好应用于多维复杂问题的寻优。本文为退役舰艇改造问题提供了解决方案，对实施项目的进度管理、迅速生成海上执法力量具有一定参考价值。

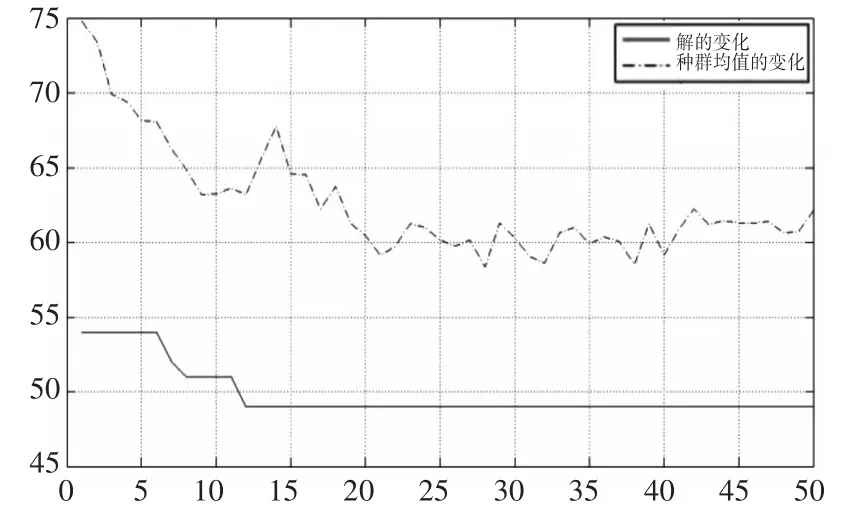
图1 算法过程

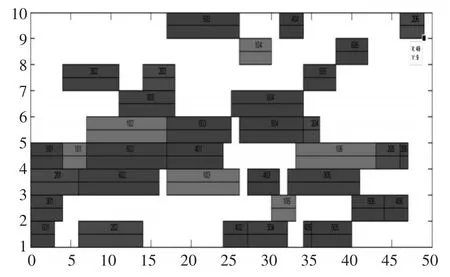
图2 最优甘特图