对“蚂蚁怎样走最近”的教学思考

张永平

“蚂蚁怎样走最近”是北师大版数学教材八年级上册“勾股定理的应用”这一内容的练习题，其目的是培养学生运用勾股定理解决实际问题的能力，学会把简单的空间图形转化为平面图形来解决。教材提出了下面的问题（如图1所示）。

根据上面的分析，教学“蚂蚁怎样走最近”时我有下面几点思考。

1.充分利用教材例题渗透分类讨论的数学思想，培养学生思维的全面性。

教师先引导学生思考蚂蚁沿侧面爬行的各种路径，掌握教材中解決问题的方法，然后提出蚂蚁沿表面爬行的问题让学生思考并解答，最后总结：要求蚂蚁沿圆柱表面爬行的最短路程，只要分别计算出沿圆柱侧面爬行和沿圆柱的点A寅点C寅点B爬行的路径长度再比较即可。

2.设计蚂蚁沿长方体表面爬行的最短路程问题，培养学生类比思考问题的能力。

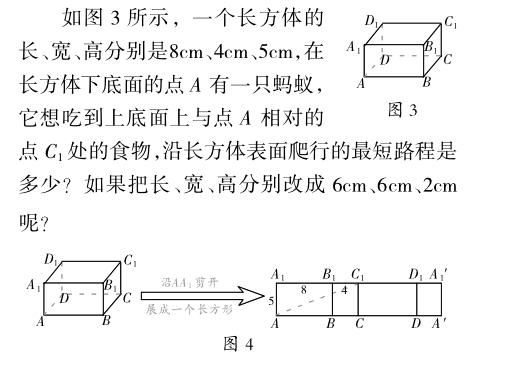
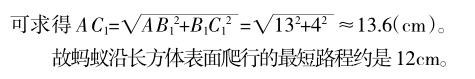
同样地，当长方体的长、宽、高分别是6cm、6cm、2cm时，蚂蚁沿长方体表面爬行的最短路程是10cm。

3.引导学生分析在蚂蚁分别沿圆柱与长方体爬行的最短路程的方法，培养学生探究问题的能力。

（1）当蚂蚁沿圆柱表面爬行时，只要计算出两种结果再进行比较即可。

（2）当蚂蚁沿长方体表面爬行时，虽然要分三种情况进行讨论，但其实只要看从A点引出的三条棱中哪条最长，沿最长的那条棱剪开展成长方形，这时路程最短。如图5，只要沿长方体的棱AB剪开，展成长方形即为最短路程。

（作者单位：甘肃省天水市秦州区牡丹中学）