基于有限元分析的两极旋转插头可靠性设计
苏彩虹 郭远平 成 瀚 张佳路
(公牛集团股份有限公司 慈溪 315314)
前言
随着科技发展,电器用品在人类生活中日益增多,插头的使用也更加频繁。为了适应于更多场合和环境,插头的结构在不断的改进。其中,旋转插头的出现便很好地解决了常规插头在狭小空间中使用的局限性。
但是现有的旋转插头在使用过程中还存在着一些问题:旋转插头内部通常是通过连接片连接插销和接线端子,常为铆接,即运动的部件为插销和连接片,而连接导线的接线端子则保持不动。但是在旋转过程中,连接片和接线端子会相对运动,旋转次数增多,铆接部长期发生接触摩擦,就会产生磨损甚至旋转不畅的问题,从而造成产品故障多发,使用寿命缩短等问题。本文以有限元分析为基础,设计一种旋转插头,将插销与接线端子直接相连,且一并设置于旋转壳中,故当旋转壳旋转时,插销与接线端子一同随着旋转壳运动,而插销与接线端子之间不发生相对运动,从而避免了使用常规技术中连接片产生磨损甚至旋转不畅的问题;采用双凸点双导轨结构,使旋转过程顺滑,给消费者最佳旋转体验;由于没有使用连接片,而接线端子上接有导线,即旋转过程中接线端子与导线是发生相对运动的,通过出线孔角度设计来限制导线的摆动幅度,从而降低导线在运动过程中因为摆动幅度大而容易与旋转插头内设置的其他零件或者散丝纠缠,降低产品故障多发率,延长产品使用寿命。
1 出线孔设计
设计旋转前盖旋转轴,在旋转轴增加出线孔通孔,电源线通过出线孔伸进接线端子中,接线端子铜螺钉压紧电源线。出线孔结构简化模型如图2所示。假设出线孔圆心与旋转轴圆心的距离为X1,旋转轴半径为R1,出线孔半径为R2,在旋转轴上设计卡线槽,假设卡线槽相对于旋转轴圆心的倾斜角度为θ1,相对于出线孔圆心的倾斜角度为θ2。当旋转轴旋转90°时,出线孔旋转角度为θ3,即旋转过程中电源线的摆幅为θ3。
根据出线孔结构简化模型示意图(图1),推出图中表示电源线摆幅θ3与出线孔圆心与旋转轴圆心的距离X、卡线槽相对于旋转轴圆心的倾斜角度为θ1的变化规律为:

因为上下盖间距16.6 mm,外接电源线最大横截面积1.5 mm2,所以旋转孔直径11.4 mm,R1=6.6 mm、R2=5.5 mm,可得 X1=0.1。
对以上关系式进行整合,可以得到X2/θ1/θ2/θ3的四阶方程:

因四阶方程中有三个关系等式,所以只需定义其中一个参数,就可以求出模型其他参数,得到出线孔结构模型。
为时模型具有最大旋转寿命,选取出线角度θ2分别为35 °/40 °/45 °,计算出出线孔位置,制作手板模型,分别接1.0 mm2/ 1.5 mm2圆线、扁线,四种规格电源线进行测试进行5 000次旋转寿命测试,观察铜线的断线率。从图2测试结果可以看出,出线方向为θ2=45 °时,插头可以达到最大旋转寿命。

图1 出线孔结构简化模型示意图
2 旋转过程力学模型
旋转插头的旋转模块结构为旋转前盖设置旋转轴结构,上下盖设置相应通孔,通过孔轴配合实现模块旋转;旋转模块侧面与下盖配合面同时设置凸点与导轨,采用双凸点双导轨结构使旋转过程平稳顺滑,同时实现0 °及90 °旋转到位提醒。通过旋转模块侧面与下盖配合面过盈配合控制旋转模块的旋转力。
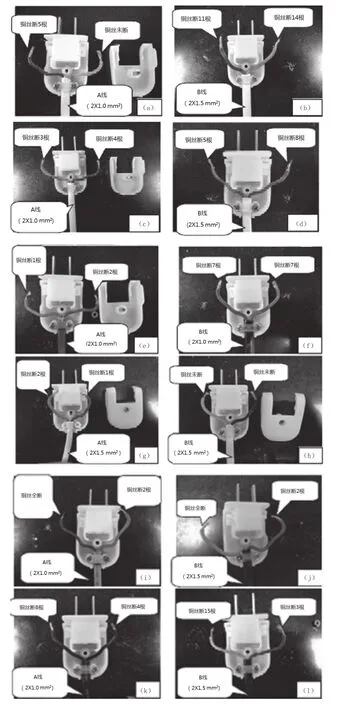
图2 寿命测试结果
通过对同类型产品客户调研发现2.5 N旋转力为最佳手感,消费者感觉到舒适的力学区间为1.7~3.5 N,所以1.7~3.5 N为产品最大旋转力范围。对旋转过程进行发现 ,当凸点滑动至定位凹槽最高点时受力最大,此位置处所需旋转力即为消费者使用时需要的最大旋转力,所以对此位置处进行受力分析。
假设旋转力施力点距离旋转轴中心距离为X1,旋转轴距离凸点圆心的距离为X2;旋转截面产生的旋转力矩为M,则:

以凸点为研究对象,建立受力模型,进行受力分析,可得:
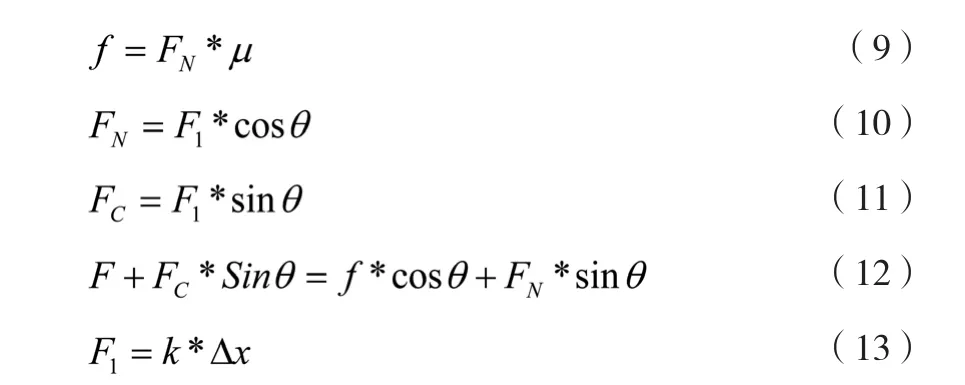
其中:
F—为对凸点所施旋转力 ;
f—为凸点所受摩擦力 ;
F1—为导轨圆弧对凸点反作用力合力 ;
FN—为正压力 ;
FC—为切力 ;
θ—为圆弧切线与X轴夹角;
k—为下盖配合面强度;
Δx—为位移变量。
因插销外露长度为16 mm,施力点为插销中点,施力点到旋转圆心的距离X1=17 mm,凸点到旋转中心的距离X2=10 mm。当F旋=1.7 N时,F=3.23 N;当F旋=3.5 N时,F=6.65 N。摩擦力f方向与接触圆弧相切,设置圆弧半径R=1.8 mm,可求得θ=28 °,假设摩擦系数μs=0.5,则可以求得F1的上下限为F1=2.6~5.4 N。
对下盖配合面的强度K通过仿真可以求得K=24 N/mm,则旋转模块侧面与下盖配合面过盈量为0.1~0.25 mm。
3 实验仿真与分析
3.1 旋转插头模型简化
为验证计算结果的准确性,对旋转插头的旋转过程进行仿真模拟,追踪旋转力。旋转模块与下盖因体积较小,内部结构复杂,下盖的弧面外形与旋转模块内部不规则的结构给建模带来了一定的难度。根据建立有限元模型的总体原则,只分析与旋转有关的部件与结构,简化模型如图7。
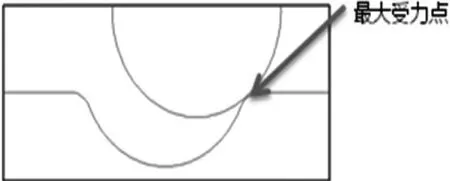
图3 最大受力点位置

图4 旋转模块力学模型
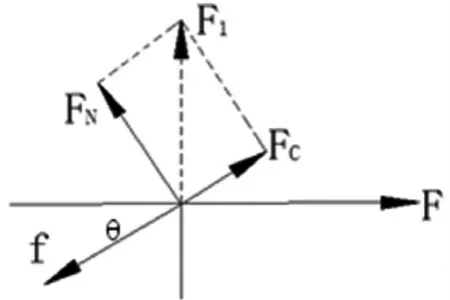
图5 凸点受力分析
3.2 旋转插头有限元模型处理
分别设置下盖与旋转模块的过盈量为0.1 mm和0.25 mm,对零部件进行网格划分及材料定义,下盖及旋转模块的材料均为PC(聚碳酸酯),其材料性能参数见表1。
下盖在配合处是六个自由度方向都被限制的,选择相应单元的节点,并将其六个自由度全都限制;对于旋转模块旋转过程五个自由度被限制,因为需要追踪凸点旋出定位槽最高点的旋转力,设置旋转模块Y轴方向旋转5 °,分10个步长运行,Y轴方向分别施加2.6 N和5.4 N的预紧力,接触面摩擦力系数μ设置为0.5 N,模型网格划分及施加载荷图如图8所示。
在施加预紧力分别为2.6 N和5.4 N时,凸点位置最大旋转力分别为1.85 N和3.4 N,数据对比结果,旋转力相对误差分别为8.8 %和4 %,有限元分析与计算结果基本吻合。
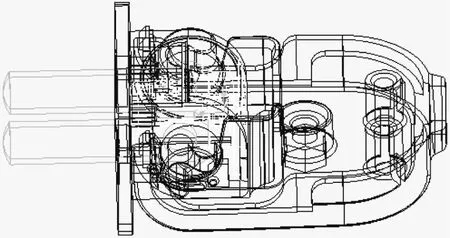
图6 旋转插头CAD模型
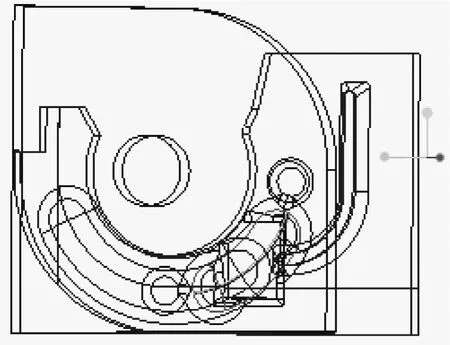
图7 旋转插头简化模型

表1 通用级聚碳酸酯的性能参数
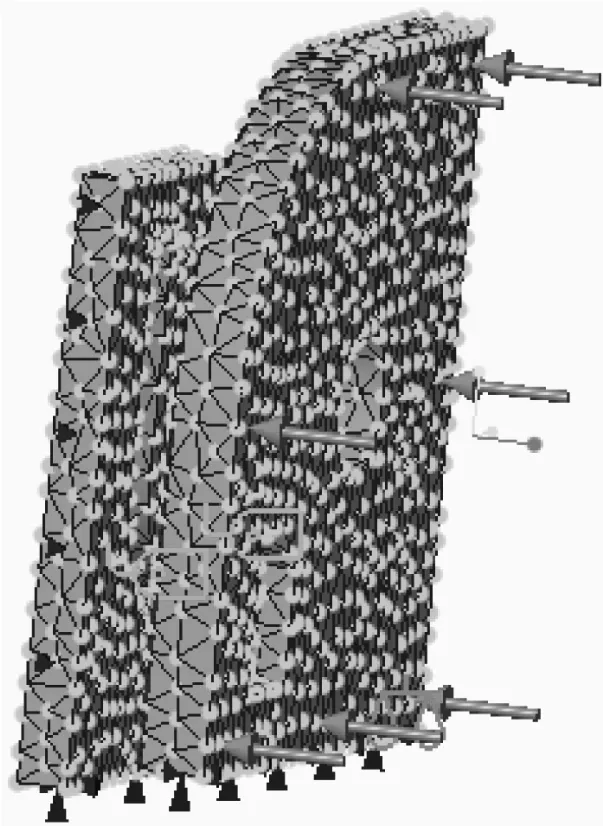
图8 模型网格划分及施加载荷图
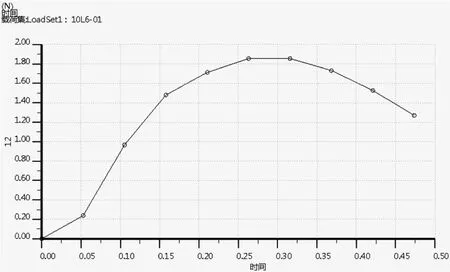
图9 预紧力为2.6 N时旋转力曲线
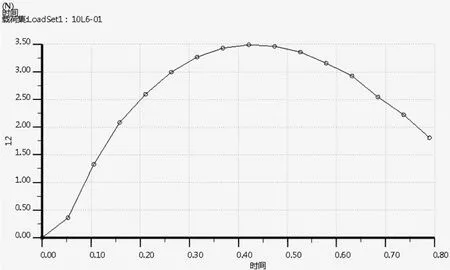
图10 预紧力为5.4 N时旋转力曲线
4 结论
1)本文对出线孔结构进行分析,建立出线孔结构简化模型,根据各参数位置关系,推出电源线摆幅θ3与出线孔圆心与旋转轴圆心的距离X、卡线槽相对于旋转轴圆心的倾斜角度为θ1的变化规律,对数学关系式进行整合,可以得到结构模型参数的四阶方程,定义出线槽角度分别为35 °/40 °/45 ° ,制作手板模型进行寿命测试,得出出线角度为45 °时,旋转插头可以达到最大寿命。
2)对旋转过程进行分析,建立旋转模块力学模型,通过对凸点进行受力分析得出当旋转模块与下盖配合面的过盈量为0.1~0.25 mm时,旋转插头的旋转力可达到1.7~3.5 N,给消费者舒适旋转体验。
3)通过旋转模块凸点力学模型计算与有限元受力分析数据对比,对比结果在施加预紧力分别为2.6 N和5.4 N时,旋转力相对误差分别为8.8 %和4 %,在CROE三维模型基础上通过Simulate 对旋转模块与配合下盖进行受力分析,为旋转结构设计提供可靠的设计依据。

