Angle-resolved spectra of the direct above-threshold ionization of diatomic molecule in IR+XUV laser fields∗

Shang Shi(石尚),Fa-Cheng Jin(金发成),and Bing-Bing Wang(王兵兵)

1 Laboratory of Optical Physics,Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2 Faculty of Science,Xi’an Aeronautical University,Xi’an 710077,China

3 University of Chinese Academy of Sciences,Beijing 100049,China

Keywords:above-threshold ionization,IR+XUV laser fields,molecular structure

1.Introduction

In the past decade,two important processes of nonlinear dynamics in intense laser field-high-order harmonic generation(HHG),in which the ionized electrons recombine with the parent ion[1,2]and high-order above-threshold ionization(HATI),in which the ionized electrons elastically collide with the parent ion[3-5]-have been widely used in the study of the molecular structure because the molecular structure is of great significance in the fields of physics,biology and chemistry.For homonuclear diatomic molecules,the results of the theories[6-9]and experiments[10,11]of HATI process indicate that the HATI spectrum carries the important information of molecules,such as internuclear separation,the symmetry of the highest occupied molecular orbital as well as the alignment of molecular axis.However,the interference structure in the HATI spectra of heteronuclear diatomic and polyatomic molecules[12-14]are more complicated than that of homonuclear diatoms.One needs to consider the in fluence of the charge distribution of molecular ions on the interference fringes.[12]Recently,the studies on the HHG process of molecules also demonstrate theoretically[14-18]and experimentally[19]that the HHG spectra can be used to expose the structure and dynamics of molecules.

Unlike the two-step processes of HHG and HATI,the direct ATI is a one-step process where the electrons reach the detector directly after the ionization.[20,21]Therefore,the ionization spectra of the direct ATI can directly reflect the initial information of the molecular properties.The results obtained by He et al.[22]who used extreme ultraviolet(XUV)pulses to study the direct ATI of H+2demonstrate that the initial probability distribution of molecules can be imaged from the angular distribution of the directly ionized electron.However,most studies do not apply the direct ATI process to explore the molecular structure because the structural information of a molecule is mainly embodied in the high-energy region of the ionization spectra where only the re-colliding electron may dominate[8-11]by applying a commonly used infrared(IR)laser field.

To gain the angle-resolved spectra of direct ATI that can fully exhibit the structural information of molecules,we consider a combined infrared and XUV laser fields to investigate the direct ATI process of a diatomic molecule.The idea of applying IR+XUV laser fields to the study of ultrafast nonlinear dynamics has already existed,see Refs.[23]-[26].In our results,the destructive interference fringes related to the molecular structure are clearly displayed in the angle-resolved spectra of the direct ATI.By comparing the direct ATI spectra of hydrogen molecule in two-color laser field with that in a monochromatic laser field,we found the different roles of infrared and XUV laser fields in the ionization of an electron.The study on oxygen molecules further manifests the universality of the method which utilizes the angle-resolved spectra of the direct ATI in IR+XUV two-color laser fields to infer the molecular structure.

2.Theoretical method

By using the frequency-domain theory,we deal with the direct ATI process of a diatomic molecule in two-color linearly polarized laser fields with laser frequencies ω1for lowfrequency field and ω2for high-frequency field.The Hamiltonian of the molecule-radiation system is(atomic units are used throughout unless otherwise stated)

where

is the free-electron and free-photon energy operator and Naj=is the photon number operator with aj()the annihilation(creation)operator of the laser photon mode.U(r)is the two-center binding potential of a diatomic molecule.V is the electron-photon interaction which is expressed as

The initial state of the system is|ψi〉=|Φi(r),l1,l2〉=Φi(r)⊗|l1〉⊗|l2〉,which is the eigenstate of the Hamiltonian H0+U(r)with energy

Here,Φi(r)is the ground-state wave function of the molecule with binding energy EB,and|lj〉is the Fock state of the laser mode with photon number lj.Meanwhile,the final state|ψf〉=|ψpfn1n2〉is the quantized- field Volkov state in twocolor laser fields[27]

which is the eigenstate of the Hamiltonian H0+V with eigenvalue

where upjis the ponderomotive energy in unit of one photon energy of the laser field.In Eq.(4),q1and q2represent the number of photons absorbed by the electron from IR and XUV laser fields,respectively.pfis the final momentum of the ionized electron. φ1and φ2are the initial phases of each laser field and are taken as zero for simplicity in this paper.The term Jq1q2(ζf)is the generalized Bessel function,which is expressed as

where the arguments of the generalized Bessel function are as follows:

Here,we define θfas the angle of the momentum direction of the final electron with respect to the polarization direction of the laser fields.

The transition matrix element of the direct ATI process from the initial state|ψi〉to the final state|ψf〉is written as[5]

By inserting the expressions of the initial state and final state into Eq.(7),the transition matrix element becomes

whereΦi(pf)is the Fouriertransform ofthe ground-state wave function ofthe diatomic molecule.Forhydrogen molecule,the ground-state wave function was obtained by a linear combination of two atomic wave functions with Gaussian forms,hence we have

Here,R0is the nuclear spacing of the molecule,θ is the angle between the momentum direction of the ionized electron and the molecular axis,and cosθ is expressed as cosθ =sinθfcosφfsinθmcosφm+sinθfsinφfsinθmsinφm+cosθfcosθm,where φmand φfare the azimuthal angles of the molecular axis and the final momentum of the electron,respectively.θmis the angle between the polarization vectors of the laser field and the molecular axis.We take φm= φf=0 in the calculation ofthe electron energy spectra,thuscosθ can be reduced to cos(θf-θm).For an oxygen molecule,the initial wave function was calculated by the GAMESS software.[12]Thus the Fourier transform of the ground-state wave function of O2is expressed as

3.Results and discussion

We first compare the angle-resolved spectra of the direct ATI for atomic hydrogen and molecular hydrogen in linearly polarized IR+XUV laser fields with both intensities of 3.6×1013W/cm2,as shown in Fig.1(a)for the hydrogen atom and Figs.1(b)-1(c)for the hydrogen molecule.The photon energy of XUV laser is ω2=15ω1,where ω1=1.55 eV is the photon energy of IR laser.The hydrogen molecular axis is along the directions of the laser polarization.The ionization potential foratomic hydrogen and molecular hydrogen are 13.6 eV and 13.12 eV,respectively.It can be seen that some destructive interference fringes(DIF)in the molecular spectra do not exist in the atomic spectrum.By analyzing the transition formula of the direct ATI process(see Eq.(8)),we found that the condition for the emergence of these DIF can be expressed as cos(pfcosθR0/2)=0.Thus,we obtain the Ef-θfcurve which can predict the position of the DIF in the angleresolved ionization spectra,as seen in Figs.1(b)and 1(c).The corresponding expression of the photoelectron energy Efis

where R0is the internuclear separation,n=0,±1,±2,....The black dashed lines in Figs.1(b)-1(c)correspond to n=0,and the red dash-dotted line in Fig.1(c)corresponds to n=1.It can be seen from Eq.(11)that the energy of the photoelectron in the DIF can get minimum value,i.e.,Efmin=π2/2R20,when n=0 with the electron emitted along the molecular axis,i.e.,θf= θm.Therefore,the DIF will appear in the spectra as long as the range of the direct ATI spectra exceed the value of Efmin.Additionally,because Efminis inversely proportional to R20,the value of Efminfor R0=6 a.u.(The unit a.u.is short for atomic unit)decreases to one ninth of that for R0=2 a.u.,hence this is the reason why the number of the DIF in Fig.1(c)is more than that in Fig.1(b).

Fig.1.The angle-resolved spectra of the direct ATI for a hydrogen atom(a)and for a hydrogen molecule with the internuclear distance R0=2.0 a.u.(b)and R0=6.0 a.u(c).The photon energy of XUV laser is ω2=15ω1,where ω1=1.55 eV represents the photon energy of IR laser.Both the photon energies of IR and XUV laser remain constant for the case of H2 in this paper.The laser intensities are I2=I1=3.6×1013 W/cm2,where I2 is the intensity of XUV laser field and I1 the intensity of IR laser field.The molecular axis of H2 is along the polarization directions of two laser fields,which are fixed at z axis.In logarithmic scale.

Fig.2.The angle-resolved spectra ofthe directATIofH2 with differentorientation anglesθm=0°(a),45°(b),60°(c),and 90°(d).The internuclear separation is 2 a.u.and remains unchanged in the following results of the hydrogen molecule.The intensities and the photon energy of each laser field are the same as in Fig.1.In logarithmic scale.

The angle-resolved spectra of the direct ATI of H2with different orientation angles of the hydrogen molecular axis with respect to the polarization vectors of the laser fields is shown in Fig.2.Parameters are the same as given in Fig.1(b).It shows that the distribution of the angle-resolved spectra and the DIF significantly depend on the angle between the molecular axis and the polarization direction of the laser.Compared to Ref.[8],where the predictive curve can overlap well with the DIF in angle-resolved HATI spectra only when the molecular axis is perpendicular to the laser polarization,we may find that the interference stripes related to the molecular structure in the spectra presented by Fig.2 can be perfectly reproduced by Eq.(11)at any orientation angle θm.This indicates that the angle-resolved spectra of the direct ATI may provide more details about the information of the molecular structure.

Fig.3.The angular distribution for the direct ATI of H2 absorbing a certain number of XUV photons,which is denoted by q2.The parameters are consistent with Fig.1(b).The solid and dashed lines predict the cutoff and the beginning position of the ATI spectra for different q2.In logarithmic scale.

To explain the plateau-like distribution of the angleresolved spectra of the direct ATI,we analyze the transition matrix element of the direct ATI process under the conditions of Fig.1(b),as shown in Fig.3.Here,q2represents the absorption number of XUV photons.Compared with q2=1,the whole spectrum moves to higher energy region when q2=2.By applying the energy conservation rule during the ionization process derived from the saddle-point approximation(see Appendix A),we predict the classical position of the beginning(dashed line)and the cutoff(solid line)of the ATI spectra with different values of q2,which match well with the numerical calculation results.Figure 3 demonstrates that the XUV laser field plays a crucial role in making the high-energy plateau on the direct ATI spectra,in marked contrast to the situation that the high-energy plateau is absent in the direct ATI spectra for IR laser case.[8,11]We can also see that the DIF conspicuously appear in the angle-resolved spectra when q2=2.This is because the minimal energy for the emergence of DIF is about 33.6 eV according to Eq.(11),and hence the electron needs to absorb at least two XUV photons to obtain such a high energy.

Fig.4.The angle-resolved direct ATI spectra of H2 in an IR laser filed with the intensity of 3.6×1015 W/cm2 at four orientation angles of the molecular axis.In logarithmic scale.

We now consider the direct ATI of the molecular hydrogen in a monochromatic laser field. Since the term cos(pfcosθR0/2)in the direct ATI transition formula originates from the coherent superposition of the ionization paths of the electron in the hydrogen molecule,the DIF in the spectra is actually unconcerned with whether or not the laser fields are two-color.Therefore,for monochromatic IR laser field,the DIF appear in the angular spectra of the direct ATI as the laser intensity is increased strong enough.Figure 4 presents the direct ATI spectra of monochromatic IR laser field with its intensity increased to I1=3.6×1015W/cm2.Compared to Fig.2 and Fig.3,it is found that the XUV laser field can raise the ionization probability in the ATI process.On the other hand,for the XUV laser field with ω2=23.25 eV and I2=3.6×1013W/cm2,the distribution of the ionization spectra totally differs from that of two-color laser fields and monochromatic IR laser field.Namely,the distribution of the electron energy is no longer continuous,and there are many minimums in the spectra,as shown in Fig.5.However,by comparing with the angle-resolved probability spectra of a hydrogen atom which absorbs the same number of XUV photons as the hydrogen molecule,we can identify the minimums resulting from the destructive interference of the electron wave packets emitted from the hydrogen molecule,where these minimums are pointed out by arrows in Fig.5.The corresponding ejection angle θfcan be used in the transformation of Eq.(11)to determine the nuclei distance of the diatomic molecule,i.e.,

Additionally,comparing Fig.5 with Fig.1,one may find that the IR laser field can broaden the kinetic energy distribution of the ionized electron and thus a continuous angle-resolved ionization spectrum may be obtained in IR+XUV two-color laser fields.

We further calculate the momentum spectra for the direct ATI process of H2in an XUV laser field with an intensity of 3.6×1014W/cm2,which are plotted in Fig.6.Here,the azimuthal angle of the final momentum of the electron φfis variable,thus the momentum spectra exhibit a continuous distribution.We can find that there are two complete destructive interference fringes(CDIF)in the momentum spectra for each alignment angle of the molecular axis.For alignment angle θm=0°,the CDIF are perpendicular to pzaxis(see Figs.6(a)and 6(c)),while for θm=90°,the CDIF are parallel to pzaxis(see Figs.6(b)and 6(d)).Because the destructive condition cos(pfcosθR0/2)=cos((R0/2)(pxsinθm+pzcosθm))=0 determines the position of the CDIF at pz=(2n+1)π/R0when θm=0°,where n=0,±1,±2,...,and at px=(2n+1)π/R0when θm=90°,where n=0,±1,±2,....Hence,the molecular internuclear distance can be obtained by R0=2π/Δpj(j=x,z)once the momentum difference Δpzor Δpxis calculated from two adjacent CDIF in the momentum spectra.

Fig.5.The angle-resolved probability spectra for the direct ATI of a hydrogen molecule(dashed line in each panel)and a hydrogen atom(solid line in each panel)in an XUV laser filed with the intensity of 3.6×1013 W/cm2.E fm denotes the energy of the electron which is ionized from the molecular hydrogen and E fa denotes the energy of the electron which is ionized from the atomic hydrogen.For the three columns from left to right,the electron absorbs one,two and three XUV photons,respectively.The molecular orientation angle θm is 0° for the top panels and 90° for the bottom panels.In logarithmic scale.

Fig.6.The ATI momentum spectra of a hydrogen molecule in an XUV laser field with an intensity of 3.6×1014 W/cm2.The upper panels are for the internuclear distance R0=2.0 a.u.and the lower panels are for R0=4.0 a.u.The molecular axis is parallel(the left)or perpendicular(the right)to the polarization directions of the two laser fields.In logarithmic scale.

To illustrate the applicability of the angle-resolved spectra of the direct ATI in IR+XUV laser fields to the exploration of the molecular structure,we calculated the angular distribution of the direct ATI for O2in IR+XUV laser fields with ω2=50ω1and ω1=1.55 eV for the same intensities as in Fig.1,as displayed in Fig.7.The internuclear distance of O2is 2.282 a.u.and the ionization potential is 12.07 eV.The wavefunction of O2in momentum representation is formulated by Eq.(10).By taking sin(pfcosθR0/2)=0,we have pfcosθR0/2=nπ,n=0,±1,±2,....When n=0,the equation cosθ=0 yields a destructive stripe in the spectra at electronic emission angle θf= θm+π/2,while when n=±1,±2,...,the predictive curve about the DIF can be expressed by the equation

The red dash-dotted lines coinciding with the butter fly wingshaped interference fringes are acquired from the minimum of|Jq1q2(ζf)|2,indicating that the butter fly wing-shaped interference fringes are attributed to the interaction between the laser fields and the ionized electron,irrelevant to the geometrical structure of molecules.

Fig.7.The angle-resolved direct ATI spectra of an oxygen molecule with an internuclear separation of 2.282 a.u.The photon energy of the XUV laser ω2=50ω1,where ω1=1.55 eV.The laser intensities are I2=I1=3.6×1013 W/cm2.In logarithmic scale.

4.Conclusion

By applying the frequency-domain theory based on the nonperturbative quantum electrodynamics,we have studied the direct ATI of diatomic molecules in linearly polarized IR+XUV laser fields.The destructive interference fringes resulting from the coherent emission of the ionized electron are perfectly reproduced at any orientation angle by a simple predictive formula,which also predicts the minimal energy value for the emergence of the DIF in the spectra.The comparison between the direct ATI spectra of a monochromatic laser field and two-color IR+XUV laser fields shows that the XUV laser field can not only raise the energy of the ionized electron,but also increase the ionization probability of the photoelectron in the high-energy region,while the IR laser field can broaden the kinetic energy distribution of the ionized electron,which clearly displays the DIF in the direct ATI spectra.The study on the direct ATI of the oxygen molecule further demonstrates that the angle-resolved spectra of the direct ATI in IR+XUV laser fields may be extensively used in the investigation of molecular structures.

Appendix A

Under the calculated conditions,the width of each energy plateau is determined by the generalized Bessel function J-q1(ζ1,ζ3),which can be expressed in the form

where f(t)= ζ1sin(ω1t)+ ζ3sin(2ω1t)+q1ω1t and T=2π/ω1.Meanwhile,the classical action of an electron is

where Ac1(t)=/ω1cos(ω1t)is the vector potential of the XUV laser field.[26]Comparing Eq.(A1)with Eq.(A2),J-q1(ζ1,ζ3)can be rewritten as

In the saddle-point approximation,the saddle-point t0satis fies f′(t0)=0,which leading to the energy conservation relation in the ionization process

This equation can predict the beginning and cutoff position of the ATI spectrum for each q2.When θf＜ π/2,the maximum energy value is

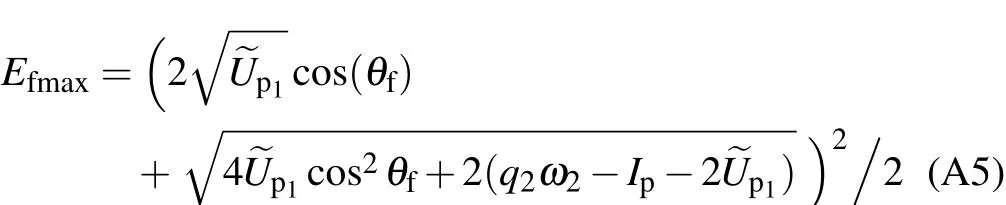
under the condition of cosω1t0=1,and the minimum energy value is

under the condition of cosω1t0=-1.When θf＞ π/2,the maximum energy value is

where cosω1t0=-1,and the minimum energy value is

where cosω1t0=1.

Acknowledgment

We thank all the members of SFAMP club for their helpful discussions.