氧化层对液态金属起始沸腾过热度的影响模型

马在勇，秋穗正，步珊珊，张卢腾，孙 皖，潘良明

(1.重庆大学 低品位能源利用技术及系统教育部重点实验室，重庆 400044；2.西安交通大学 动力工程多相流国家重点实验室，陕西 西安 710049；3.西安交通大学 核科学与技术系，陕西 西安 710049)

在钠冷反应堆的设计和安全分析中，起始沸腾过热度是一个重要的参数，可能影响后续的沸腾过程，如流型演化、沸腾传热和沸腾临界。相关研究集中于20世纪60～80年代，近些年的研究极少。但至今为止，对于相关机理的研究和参数的分析还存在着很多不足。

在洁净的固体金属表面上，由于液态金属良好的浸润特性，大的孔穴处于浸润状态，不能成为潜在的汽化核心。在不考虑惰性气体的影响下，小的汽化核心势必导致极高的起始沸腾过热度，实验上也观察到了这种现象。然而，在完全排除惰性气体影响的情况下，有些实验中也观察到了极低的过热度，这表明在实际系统中存在尚未被浸没的较大的孔穴。

氧化层的存在被认为是阻止气液界面深入较大的孔穴并将之浸没的重要因素。在固体表面常存在着非金属杂质，这些杂质多为氧化物，它们均不易被液态金属浸润，带有氧化层的壁面孔穴具有较大的尺寸，其核化所需的过热度较小，有利于降低起始沸腾过热度[1]。引入了氧化层影响的Holtz压力-温度历史模型[2]在解释实验数据上取得了一定成功，但在进行核化半径计算时，若直接采用沸腾前稳态阶段的气液界面半径，许多实验测得的过热度与理论计算值不符，需对核化半径引入修正因子γ。后续研究者针对该修正因子进行了许多研究[1,3-5]，在不同的研究结果中，该值小于1、等于1、大于1的情形均有出现。目前多数研究中常采用恒定的γ值，缺少更为符合实际的计算关系式形式。

本文拟对氧化层对液态金属起始沸腾过热度的影响开展分析，研究氧化层作用下核化半径的计算方法，建立氧化层对液态金属起始沸腾过热度的影响模型。

1 基本模型

假定壁面孔穴为锥形，孔穴的几何尺寸可利用半锥角θ及穴嘴半径rmax进行描述。另外，考虑到氧化层的影响，引入氧化层位置参数rc。假定从孔穴底部开始，氧化层仅能覆盖孔穴的部分壁面，形成锥形的氧化层薄膜，氧化层位置定义为该锥形薄膜的锥底圆面半径。本文模型假定在氧化层位置之上完全不存在氧化层，氧化层位置之下存在均匀的、厚度可忽略的氧化层薄膜。氧化层的基本特性是润湿性差，液钠难以浸润，而裸露的壁面则很容易被浸润，因此氧化层位置是物理过程中的孔穴穴嘴，鉴于此，本文模型中仅采用半锥角及氧化层位置对孔穴进行描述。

液态金属加热至核化前存在一段参数相对稳定的时间，这一过程中，气液界面逐渐稳定，惰性气体逐渐扩散，总体上使得核化变得难以进行，因而称之为去活化过程。本模型假设在此段时间末期，气液界面位于氧化层位置，且在随后沸腾过程中，根据操作过程的不同，可发生两种不同类型的核化，如图1所示。在不发生明显的运行压力增大的情况下，相界面在加热或降压作用下直接变形，完成核化过程，称为直接核化(图1a)；在加热阶段同时伴随加压的情况下，相界面可能在压力的作用下进行界面移动同时伴随核化，本模型中简化为界面移动后的核化过程，即先进行界面移动，后进行核化(图1b)。图1b的简化主要是考虑到在计算中压力的作用可瞬间完成，而由加热导致的界面变形过程通常较慢。加压过程中界面进一步深入孔穴，本模型中归入去活化过程，称为二次去活化，而通常的去活化过程称为一次去活化。

由于氧化层的非浸润性，接触角θr很大，在完全非浸润的情况下可达到π(180°)。但事实上，由于氧化层表面微结构等特性的影响[6]，接触角可在一定范围内变化。图1的两种核化过程中，γ均定义为核化发生时的界面半径与去活化末期的界面半径之比。下面对两类核化过程分别进行分析。

对于直接核化过程，在核化末期存在浸润性的突变，最终核化半径为氧化层位置rc，而对于去活化半径，仅能确定其最小值rc/cosθ，因此：

(1)

对于界面移动后的核化过程，对于去活化半径，假定界面变形远较界面移动容易，可取界面移动末期的接触角为0°,因此对应去活化半径为rmin/cosθ。对于核化半径，核化始于界面最深处的界面位置为rmin，由于氧化层表面微观结构特性，核化角随核化过程的剧烈程度变化，因此对于核化半径，其最小值为rmin。同时考虑到氧化层位置润湿特性的突变，核化半径受到氧化层位置的限制，其最大值为rc，即：

a——直接核化；b——界面移动后的核化图1 两类核化过程 Fig.1 Two types of nucleation processes

(2)

由此可看出，在第1类核化下，γ不大于1，第2类核化下，γ可能大于1，等于1或小于1。

在起始沸腾计算中，最为关键的是获得核化半径。对于第1类核化过程，核化半径等于rc。对于第2类核化过程，核化半径的取值为一定范围，但考虑到实际情况下不同核化角的概率并不相同，本模型中拟采用最佳估算值进行处理。

根据Dwyer等[7]的实验结果，加热过程的快慢影响最终的过热度，但其研究同时显示，温度上升率超过0.2 K/s左右，加热速度的影响已不明显。一般认为，对于多数沸腾过程，加热过程相对较快。可认为绝大多数加热过程的核化半径接近其界面位置处可能达到的最小核化半径。

在第1类核化中，其rc同时也是其rmin。在第2类核化中，模型中包含了先进行界面移动，后进行核化的假设，实际上两者可能是同时进行的，因此，最终的核化半径应略高于rmin；同时随rmin的减小，界面的移动难度增大，很小的核化半径出现的可能性较低。第2类核化半径的最佳估计值应满足在rmin足够小时接近rmin同时又不能太小的条件。图2示出常用的平均数计算方法，可看出，几何平均数较为合适，因此本模型中快速加热下的核化半径Rmin估计值为：

(3)

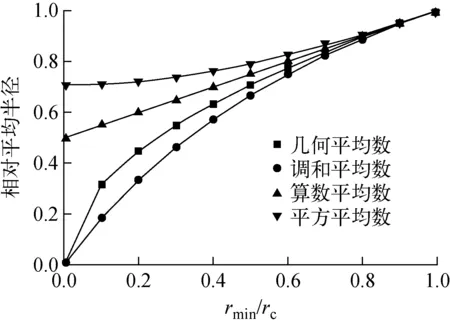
图2 不同的平均数算法Fig.2 Different arithmetics of mean value

容易看出，式(3)也适用于第1类核化。在本文模型中，去活化末期对应系统压力最高、惰性气体浓度最低的时刻，对应的界面位置达到rmin。去活化半径Rm可根据气液界面的平衡获得：

(4)

式中：σ为表面张力；p为压力；m表示去活化末期；v、g、l分别表示蒸汽、惰性气体及液体。

对于rmin的计算两类核化有所不同。对于第1类核化，rmin为rc；对于第2类核化，根据本文模型假设，取接触角为0°，可得rmin表达式：

(5)

由此可得到本模型的最佳估算γ关系式：

(6)

或核化半径的表达式：

(7)

2 模型验证

2.1 氧化层位置计算

对于第1类核化，核化半径等于rc。图3示出Holtz[8]实验数据与计算曲线的比较。实验中去活化压力高于沸腾压力且惰性气体的影响可忽略不计，按照本文模型，相关实验属于第1类核化过程。图3中分别采用核化半径的修正因子方法及核化半径直接计算法对实验数据进行了拟合，可看出修正因子γ=0.5、0.342均小于1，与本模型预测相一致。另外可看出，直接使用rc=5、3 μm也可很好地拟合实验数据。因此依据本文模型，图3中的氧化层位置为3～5 μm。这一结果与Shekriladze等[9]的推荐值5 μm相一致，另外，Holland等[1]的分析表明rc的值在0.1～10 μm，而他们对实验数据的分析显示范围为0.72～3.5 μm。本文模型与实测结果相符。

图3 0.034 MPa、538 ℃去活化参数下钠的起始沸腾过热度Fig.3 Sodium incipient boiling superheat with deactivation parameter of 0.034 MPa and 538 ℃

2.2 过热度计算

Chen[3]进行了大量实验以探究一次去活化压力、一次去活化过冷度及起始沸腾压力对过热度的影响，其中许多实验数据较Holtz压力-温度历史模型预测值偏低，即γ大于1。实验的主要参数列于表1。利用本文模型进行了分析。

表1 Chen实验的主要参数Table 1 Main parameter of Chen’s experiment

计算中取氧化层位置rc为3.5 μm，假定回路冷阱温度为630.7 K，惰性气体初始浓度假设为相应一次去活化压力下冷阱温度对应的饱和浓度。

图4示出一次去活化过冷度对起始沸腾过热度的影响。图4a由于一次去活化压力p′较低，属于第2类核化过程。图4a给出第2类核化过热度的实验数据和模型分析结果，实验数据和计算结果均表明一次去活化过冷度对起始沸腾过热度影响很小。随过冷度的增大，计算所得过热度在略微上升后略微下降，但相对于实验数据的分散程度，这种变化并不大。总体上本模型很好地预测了实验数据。

图4b相关数据属于第1类核化过程。如图4b所示，起始沸腾过热度受一次去活化过冷度的影响不大。在一次去活化过冷度较低时，从实验数据和理论曲线中均可看到一反常区域，这是因为一次去活化压力下的一次去活化温度高于沸腾阶段压力对应的饱和温度，因此在减压之后就已存在着一过热度，而当所需的起始沸腾过热度低于该值时，这一过热度即成为过热度的理论预测值。

a——低一次去活化压力；b——高一次去活化压力图4 一次去活化过冷度对起始沸腾过热度的影响Fig.4 Effect of first deactivation subcooling on incipient boiling superheat

图5 沸腾压力对起始沸腾过热度的影响Fig.5 Effect of boiling pressure on incipient boiling superheat

图5示出一次去活化参数保持不变的条件下，起始沸腾过热度与沸腾压力之间的关系。可看出，总体上理论预测值与实验数据符合良好，起始沸腾过热度随沸腾压力的增加而逐渐降低。当沸腾压力低于一次去活化压力时，这种降低主要取决于液态金属的物性，惰性气体的作用可忽略。当沸腾压力高于一次去活化压力时，发生第2类核化过程，由于界面在压力下深入孔穴，惰性气体的作用较为明显。

3 结论

本文提出了氧化层对液态金属起始沸腾过热度的估计模型，并利用实验数据进行了验证，符合良好。通过本文的研究可得到如下结论：

1) 按照界面移动方式的不同，核化可分为直接核化和界面移动后的核化，两者在计算方法上有所不同；

2) 考虑氧化层影响的核化半径介于氧化层位置处和界面最深位置处之间，其最佳估算结果可采用两者的几何平均值；

3) 压力-温度历史模型中的核化半径修正因子γ在不同条件下的取值不同，应采用关系式计算而不是采用恒定的值。