湿法配合浸出难溶物溶解度的研究

任 晋

（中国有色金属建设股份有限公司，北京，100029）

在现代湿法冶金及一些化工过程中，经常利用合适的配体来浸出难溶物MmAa，如对NH3-NH4Cl-H2O体系采用浸出法直接从低品位氧化锌矿提取锌，锌以锌氨配合物形式进入浸出液[1]；在铜、铅阳极泥的湿法处理中，利用氨水或者亚硫酸钠来浸出物料中的氯化银等。难溶物-配合体体系是一类非常重要的反应体系，也是十分复杂的体系。从配位化学的角度研究配位体和pH值对难溶物的溶解度问题，具有重要的理论和实际意义。但目前尚没有一套完善的溶解度计算模型，或者建立的模型只针对某一个具体的体系。作者利用Maple数学软件计算出难溶物的溶解度，并且绘制出相应的金属浓度-配体浓度-pH曲面图。

Maple是加拿大滑铁卢大学(University of Waterloo)和Waterloo Maple Software公司注册的一套数学软件包，以加拿大国旗图案枫叶(Maple)命名。它是当今世界上最优秀的几个数学软件之一，并以良好的使用环境、强有力的符号计算、高精度的数值计算、灵活的图形显示和高效的编程功能，成为科研人员进行数学处理的工具[2-4]。

1 各种反应平衡方程式

难溶物MmAa与某配体L形成配合物进入溶液，溶液中主要存在以下反应[5]：难溶物MmAa的离解反应；溶液中金属离子M与配体L的配合反应；溶液中金属离子M与OH的配合反应；溶液中M与A发生的自配位反应；溶液中A与H的加质子反应；溶液中配体L与H的加质子反应。此外还有水的离解反应等。

1.1 难溶物MmAa的离解反应

难溶物MmAa进入水溶液后，发生的离解反应为：

溶度积常数为：

由于A是由难溶物MmAa溶解后进入溶液的，因此

1.2 溶液中金属离子M与配体L的配合反应

M与L形成配合离子的反应平衡方程式为：

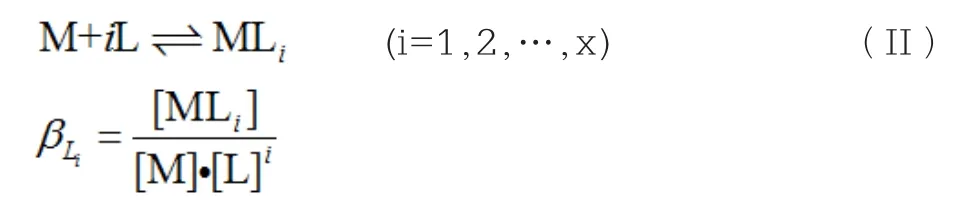
1.3 溶液中金属离子M与OH的配合反应

M与OH形成配合离子的反应平衡方程式为：

1.4 溶液中M与A发生的自配位反应

溶液中可能发生M与A的自配位反应：

1.5 溶液中A与H的加质子反应

如果A为弱酸根，则A可能与H发生加质子反应：

1.6 溶液中配体L与H的加质子反应

溶液中配体L与H发生加质子反应的平衡方程式为：

1.7 其他反应

水的离解平衡反应方程式为：

2 数学模型的构建

根据同时平衡原理和质量平衡原理[6]，由平衡反应式（I）～（Ⅶ）可得溶液中M的总浓度[M]T、配体L的总浓度[L]T、A的总浓度[A]T的质量平衡方程式分别为：

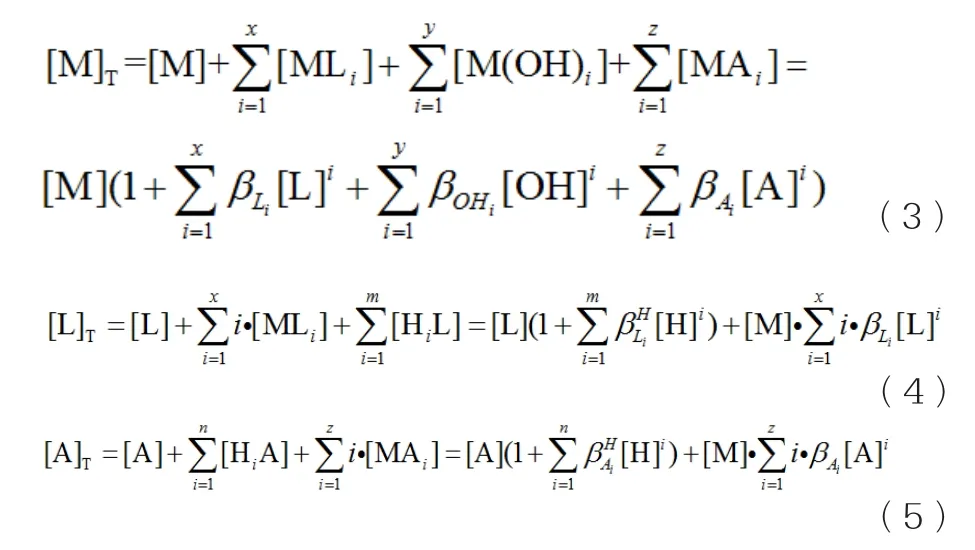
式（1）～（5）中 共 有[M]T、[M]、[L]T、[L]、[A]T、[A]、pH七个变量，因此固定[L]T、pH两个变量，根据这五个方程即可分别求出其余的变量。

由式（1）可变化为：

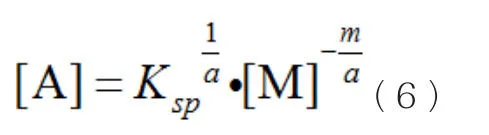
由式（4）可变化为：

由式（2）、（3）、（5）、（6）可变化为 ：

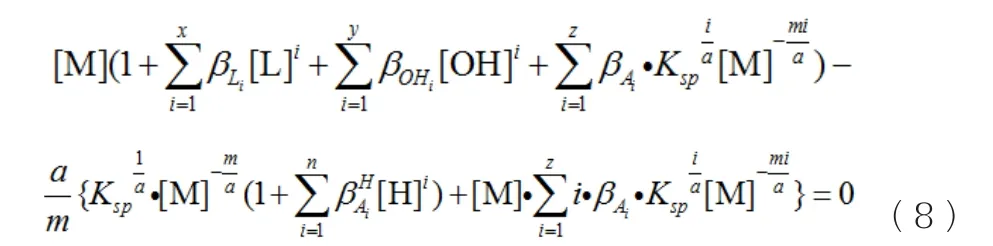
计算思路为 ：由式(7)和(8)可知共有[M]、[L]T、[L]、pH四个变量，而[L]T和pH已经固定，因此联立这两个方程组，根据maple7的solve函数即可分别求出[L]和[M]，然后将[M]代入式(6)求出[A]，最后将[M]、[A]和[L]代入式(3)即可求出[M]T。

事实上，溶液中很少发生M与A的自配位反应。若溶液中不发生M与A的自配位反应，则式(7)和(8)中可以去掉M与A的自配位反应部分，式(7)简化后的数学模型见式(9)，式(8)简化后的数学模型见(10)：

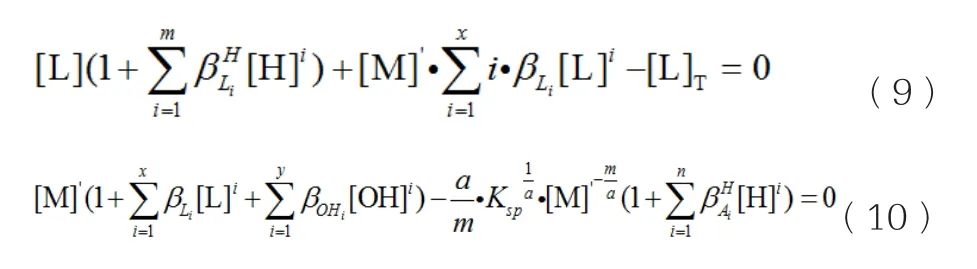
3 实例分析

以氨水浸出氯化银为例来验证建立的数学模型。氨浸氯化银过程中可能发生的配位反应及积累稳定常数见表1。

由于Ag+能与Cl-发生自配位反应，因此将这些相关的积累稳定常数及溶度积常数代入到式(7)和(8)，建立的数学模型见式(11)～(13)，然后分别求出[Ag+]及[NH3]，最后求得总银浓度[Ag]T。

表1 氨浸氯化银过程中可能发生的配位反应及积累稳定常数

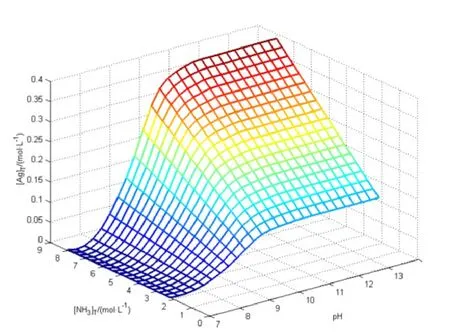
图1 [Ag]T随pH和[NH3]T变化的曲面图

图2 银的主要物种分布图

图3 [Ag]T与pH的关系

图4 [Ag]T与pH的关系

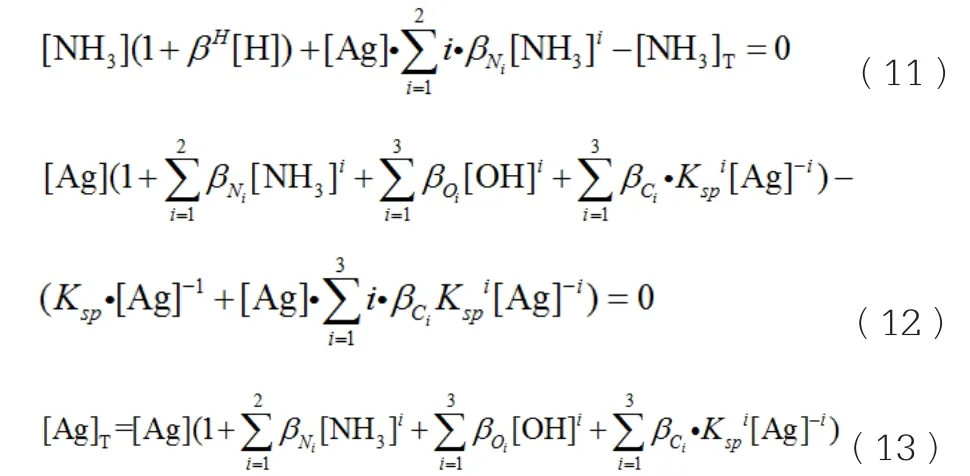
计算过程中[NH3]T分别取2、4、6、8 mol·L-1，pH分别 取7，8，9，10，11，12，13，14。将[Ag]T随[NH3]T和pH的变化关系绘制成热力学曲面图，如图1～图2所示。

图1说明当pH＜7，[NH3]T＜8 mol·L-1时，AgCl在氨水中的溶解度＜0.00236 mol·L-1；当7＜pH＜11时，提高pH值可提高银的溶解度；当pH＞11时，银的溶解度是个水平曲面，不随pH值变化而变化。图2说明银主要以Ag(NH3)2+形式存在。

为了与文献相比较，将以上将[Ag]T随[NH3]T和pH的变化关系绘制成二维图，如图3所示。经对照得出，图3所示图形和文献中[7]计算所得的图形如图4相比较完全吻合。

4 结论

本文利用配合物位化学理论，对难溶物在配体中的溶解度进行一系列计算，建立了难溶物MmAa溶解度的数学模型，并以实例进行验证，发现计算值和文献数据能很好的吻合，对其他难溶物的溶解度计算有一定参考意义。