基于量子混沌映射降低OFDM系统PAPR的算法研究

马英杰，赵耿，魏占祯，李兆斌，鞠磊

（北京电子科技学院，北京 100070）

1 引言

正交频分复用（OFDM，orthogonal frequency division multiplexing）技术是一种多载波调制技术，作为一种可以有效对抗信号波形间干扰的高速传输技术，是下一代网络物理层的核心技术。但其存在较高的峰值平均功率比（PAPR, peak to average power ratio）问题，导致信号在传输过程中产生非线性失真，通信质量下降。目前，降低OFDM系统的PAPR一般有三类方法：信号预畸变技术、编码方法、扰码技术。其中，信号预畸变法破坏了子载波之间的相位，编码方法受限于子载波个数和调制方式，所以扰码技术成为降低PAPR的主要方法。

扰码技术中的选择性映射（SLM, selective mapping）算法结构简单，效果显著，但存在较大的边带信息且运算复杂度较高的不足，因此，许多研究者对SLM算法进行改良。文献[1]提出的循环SLM 算法忽略了边带信息并且只做了一次快速傅里叶逆变换（IFFT，inverse fast Fourier transform）变换，在时域内对原始信号及其周期移位信号相加，选择最小PAPR作为候选信号。文献[2]提出了基于多混沌的时频域加密技术和 SLM峰均比抑制算法，采用Lozi和loigstic混沌映射在时频域内扰乱子载波，并且在100 km单模光纤中安全传输8.9 Gbit/s的加密OFDM信号。文献[3] 提出了基于非对称截断光正交频分复用可见光系统的低复杂度最小幅度差译码器，从而改进 SLM 算法。文献[4] 提出了一种降低十六进制正交幅度调制OFDM 信号峰均比的方法，该方法将混沌序列与SLM算法相结合，使混沌序列能够控制相位旋转因子的产生。文献[5]提出了基于Lehmer随机相位序列矢量的 SLM 改进算法，将边带信息嵌入到十六进制 PSK调制信号中进行发送。文献[6]提出了OFDM系统中使用SLM算法降低峰均比时不需要边带信息估计的接收机检测算法。文献[7]提出改进的SLM算法，将交织离散余弦变换（IDCT，inverse discrete consine transformation）变换与脉冲成形技术结合，从而降低收发端的PAPR。文献[8]提出对信号进行时域的循环移位相加减和序列组合的方法来减小PAPR。文献[9]提出了一种低复杂度的改进SLM算法和μ律压缩方案，从而降低正交频分多址接入（OFDMA，orthogonal frequency division multiple access）系统的PAPR以及计算复杂度。文献[10]提出了一种无边带信息的低复杂度 SLM 改进算法，从而降低相干光OFDM系统的PAPR。文献[11]提出了一种用于 Alamouti差分空频分组编码-正交频分复用（DSFBC-OFDM，differential space frequency black coded-OFDM）系统的盲差分SLM改进算法，从而降低系统的PAPR。

在OFDM系统中，信号峰值功率的发生时间不确定，所以数模变换器和功率放大器需要的线性动态区间较大。然而在实际应用中，信号幅度远远小于该峰值，如果以该峰值为指标设计功率放大器，将大大降低利用率，增加系统成本。此外，过高的 PAPR值会导致信号失真，破坏子载波的正交性，产生互调干扰和带外辐射，严重影响系统的性能。因此，本文提出基于量子混沌映射的改进选择性映射算法，旨在降低OFDM系统过高的PAPR。

2 基于量子混沌映射的改进选择性映射算法

2.1 传统SLM算法

传统SLM算法是一种无失真降低OFDM信号峰均比的方法，具体步骤如下。

步骤1设IFFT的输入信号为X，如式（1）所示。

发送端产生M个不相同且长度为N的随机相位序列矢量，如式（2）所示。

步骤2将这M个随机相位序列矢量分别与输入信号X进行点乘运算，得到M个不相同且长度为N的输出序列，如式（3）所示。

步骤3对这M个不同的输出序列（m）x分别进行IFFT运算，从而得到时域上的M个输出序列，如式（4）所示。

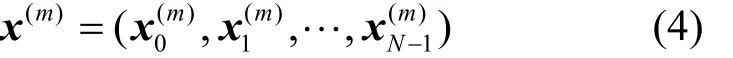
步骤4在这M个时域输出序列里选择PAPR性能最好的一组。

随着随机相位序列矢量数M的增加，系统进行IFFT变换的次数也会增加，从而增加了传统 SLM算法的复杂度。当子载波数为 128，随机相位序列矢量数M分别为2、4、6、8时，传统SLM算法的PAPR性能如图1所示。

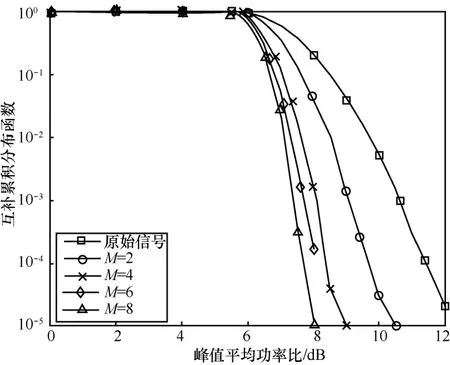
图1 不同随机相位序列矢量下传统SLM算法PAPR性能曲线

从图1可以看出，传统SLM算法的PAPR性能与随机相位序列矢量数成正比，M越大，则系统的PAPR性能越好，但是算法的复杂度也会增加。

2.2 量子loigstic混沌映射

El-Latif等[12]通过反冲转子模型方法将传统loigstic混沌映射量化，产生量子loigstic混沌映射。本文采用量子 loigstic混沌映射数字化后作为随机相位序列矢量，如式（5）所示。

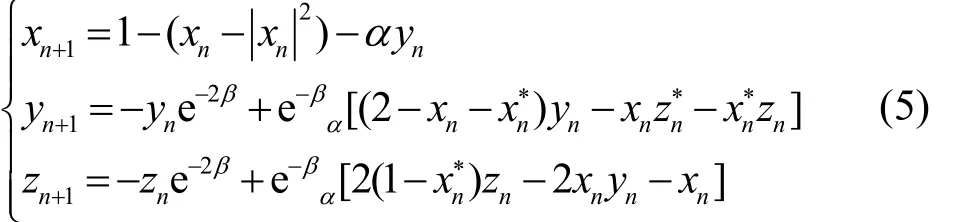
其中，α是可调参数，β是耗散参数，xn、yn和zn是系统状态参数，和是xn和zn的复共轭。当时，系统是混沌态。

本文采用量子 loigstic混沌映射数字化后作为随机相位序列矢量。与传统伪随机序列相比，量子混沌序列可以提供数目众多、易于产生和再生的信号，具有良好的相关性和随机性，克服了传统伪随机码互相关函数存在大量尖脉冲的缺陷。通过引入终端扰动，量子loigstic混沌映射解决了传统loigstic混沌映射的不动点和稳定窗问题，提高了浮点运算的精度。

传统SLM算法是一种无失真峰均比抑制算法，优点是不会导致信号的畸变，但是在系统接收端需要知道所选择的随机相位序列才能解调。所以除了传输数据信息，还需要传输对应的随机相位序列，大大增加了传输的边带信息，使其在实际应用中受到限制。对于传统 SLM 算法，接收端正确恢复原信号需要传输被选中的随机相位序列矢量，需要传输整个序列，即则信息量为N；而本文使用量子loigstic混沌映射产生伪随机序列，序列由初始值迭代产生，只需传输其初始值，降低了运算复杂度，减少了传输的边带信息，从而降低了系统的边带功率。

2.3 量子loigstic改进选择性映射算法

针对传统 SLM 算法边带功率大，候选序列数量少的缺点，本文提出了量子 loigstic改进选择性映射（QL-MSLM，quantum logistic-modified selective mapping）算法，采用分割方法将原始信号分割为实部信号和虚部信号，采用量子 loigstic混沌映射代替传统伪随机序列作为随机相位序列矢量分别与实部信号和虚部信号进行点乘运算，然后进行 IFFT变换，实部候选序列与虚部候选序列组合后计算PAPR，选择最小PAPR进行传输，具体原理如图2所示。

图2中，OFDM数据块为s（t），对串行输入的信号s（t）进行符号映射，通过串并变换分成2M个子信道，采用分割方法将信号s（t）分割为实部信号和虚部信号，分别在M个子信道上进行传输。采用量子loigstic混沌映射生成M个不同的长度为N的随机相位序列矢量P，则第m个随机相位序列矢量为第u个数据块分割为实部su_r（t）和虚部su_i（t），分别与第m个随机相位序列矢量Pm点乘运算，然后进行 IFFT

图2 量子loigstic改进选择性映射算法的原理

其中，⊗是 2个矢量间的点乘运算，IFFT是离散傅里叶逆变换，是实部候选序列，是虚部候选序列。实部信号的候选序列和虚部信号的候选序列如式（8）所示。进行线性组合得到候选传输序列

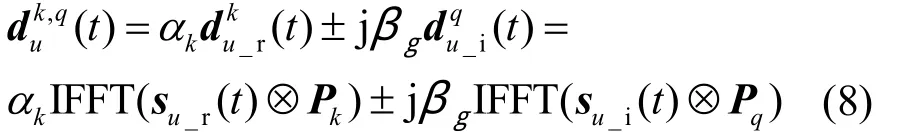
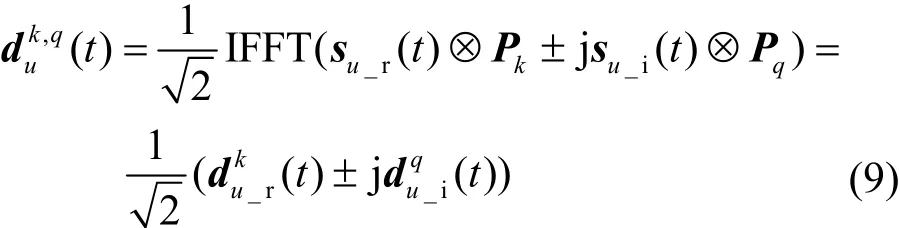
第u个数据块的候选传输序列中选择PAPR最小的一组记为Xu， 则

故输出序列为

3 系统数值仿真分析

本文采用QPSK调制，子载波数为128，通过互补累积分布函数（CCDF, complementary cumulative distribution function）来描述系统峰均比的分布情况，采用文献[13]提出的选定数据方法（SDU，selected data utilization），根据特定的选择条件来旋转相位因子，从而对传统SLM算法的PAPR性能进行改进。本文所提的QL-MSLS算法与传统SLM算法以及SDU算法的PAPR性能比较如图3所示。本文的数值仿真中，变量orignal是1×128的原始信号PAPR值。

图3 3种算法的PAPR性能对比

在传统SLM算法中，把1×128的原始信号作为输入数据，复制L组点乘随机相位序列矢量，进行IFFT计算，得到PAPR值，变量SLM是L组候选序列中最小PAPR值。采用随机相位序列矢量的传统SLM算法要求传输每个子信道的随机相位序列矢量信息，因此需要传输的边带信息量非常大，不仅增加了系统的复杂度，而且降低了系统的效率。

在本文提出的QL-MSLS算法中，把1×128的原始信号作为输入数据，复制L组，分割数据的实部和虚部，量子loigstic映射产生L组随机相位序列矢量，实部信号与虚部信号分别点乘随机相位序列矢量，然后计算IFFT后，实部数据和虚部数据线性组合。算法把候选序列扩展为L2组，变量LSLM是L2组候选序列中最小PAPR值。

从图3可以看出，与传统SLM算法以及SDU算法相比，本文提出的QL-MSLS算法更加有效地降低了系统的 PAPR。本文算法采用分割方法与线性组合变换扩展了候选序列数量，减小了算法的计算量，可以更高效地传输数据。

对于传统 SLM 算法，要在接收端正确恢复原信号需要传输被选中的随机相位序列矢量，需要传输整个序列，大大增加了边带信息，增大了边带功率。采用本文提出的QL-MSLM算法只需传送量子混沌映射初始值就可以表示一组随机相位序列矢量，使用Matlab仿真的边带功率谱如图4所示。

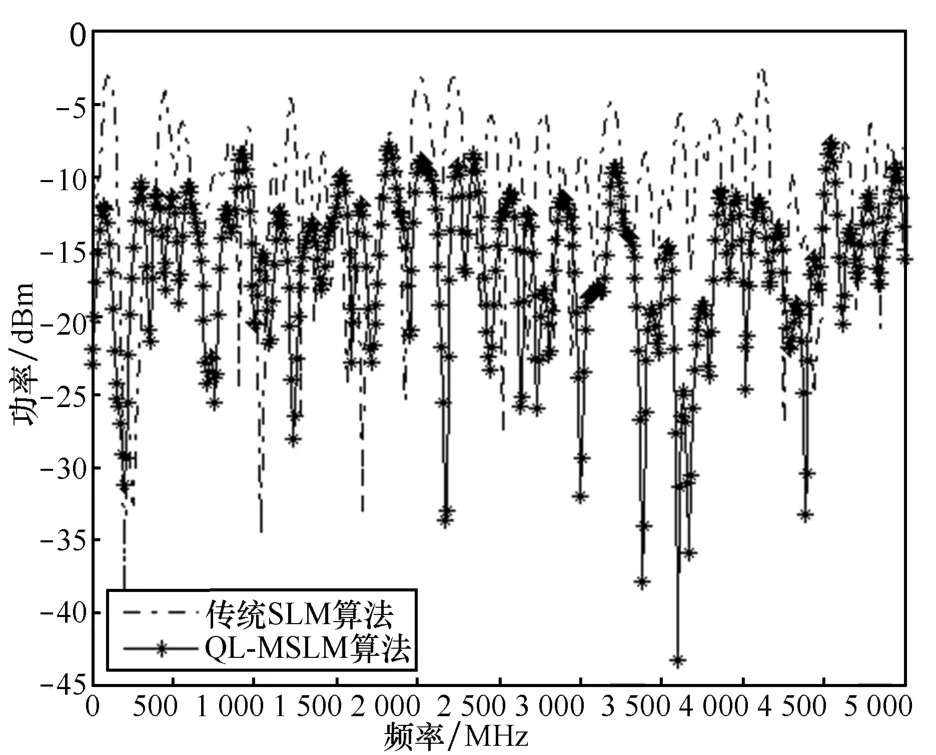
图4 边带功率谱

本文采用量子 loigstic混沌序列替代传统伪随机序列作为随机相位序列矢量，只需要一个初始值就可以表示一个随机相位序列矢量。量子混沌序列不需要存储每个序列点的值，有效减少了冗余信息的传输量。提出的算法在传输边带信息时，只需要传输一个初始值即可，不需要传输每个子信道的相位信息。从图4可以看出，QL-MSLM算法与传统SLM算法相比，大大降低了边带信息传输量，减小了边带功率，提高了系统传输效率。

4 结束语

针对传统 SLM 算法边带功率大，候选序列数量少的缺点，本文对传统 SLM 算法进行了改进，提出了量子 loigstic改进选择性映射算法（QLMSLM），解决了OFDM系统的高PAPR问题。采用量子 loigstic混沌映射代替传统伪随机序列作为随机相位序列矢量，解决了传统 loigstic混沌映射的不动点和稳定窗问题，提供了数目众多、具有良好的相关特性和随机特性、易于产生和再生的信号，降低了系统的边带功率。采用分割方法将原始信号分割为实部信号和虚部信号，采用量子loigstic混沌映射代替传统伪随机序列作为随机相位序列矢量分别与实部信号和虚部信号进行点乘运算，然后进行 IFFT变换，实部备选序列与虚部备选序列组合后计算 PAPR，选择最小 PAPR进行传输。Matlab仿真结果表明本文提出的算法更加有效地降低了系统的 PAPR，扩展了候选序列数量，减小了算法的计算量，可以更高效地进行数据传输，有效减少了冗余信息的传输量，大大降低了边带信息传输量，减小了边带功率，提高了系统传输效率，该方案在OFDM技术中具有广阔的应用前景。