含功率扰动电力系统混沌振荡的动态滑模控制

闵富红，马汉媛，王耀达

（南京师范大学电气与自动化工程学院，江苏 南京 210023）

1 引言

电力系统是由发电机、变电所、输配电线路、电力负荷等组成的复杂非线性系统，是一种耦合性强且变量多的动态系统。随着电力系统的发展和用电需求的增加，电网结构和电气设备特性高度复杂化，由参数变化、时间延迟和外部干扰等因素引起的混沌振荡会给电网的安全可靠运行带来威胁。混沌振荡是一种包含不稳定轨道的、敏感依赖性的运行，是一种极其复杂的运行形式，其不稳定性和敏感依赖性对电网安全运行构成了威胁[1]，因此促使学者们针对此现象做了诸多研究工作，分析了各种电力系统的动态特性和混沌机理[2-3]。Ji[4]讨论了激励硬限幅环节对四阶电力系统的影响，发现该系统经历了全局分岔进而导致持续的混沌行为。Min和Ma[5-6]分析了互联电力系统的动力学行为，研究了电磁干扰的灵敏度和延迟时间，并阐述了其在电力系统中的共存现象。

电力系统中出现的混沌振荡具有复杂的机理，其存在可能会导致整个系统的稳定性丧失，引起电压崩溃甚至灾难性停电，但是基于线性控制理论的传统稳定性策略不能有效地对其进行抑制，因此学者们也提出了许多非线性方法用于混沌控制，如反馈控制[7-8]、自适应控制[9-12]、线性耦合[13]、滑模控制[14-16]、模糊控制[17]、激活反馈控制[18]等，其中许多方法适用于高度非线性的大系统如电力系统。Ni[19-20]分别设计了模糊快速终端滑模控制器和快速固定时间非奇异终端滑模控制方法，来抑制电力系统中的混沌振荡。Si[21]设计延迟反馈控制器用于抑制风力涡轮机的分数阶永磁同步发电机模型中的混沌振荡。可见，滑模控制器的“结构”并不固定，其主要机理是根据系统所期望的动态特性来设计切换面，通过控制律迫使系统状态在该平面上运动。控制器的设计与系统参数和扰动无关，具有响应快速、对参数变化和扰动不灵敏以及物理实现简单的优点，能够更好地适应电力系统非线性强、变化剧烈、扰动因素多、参数不稳定等特征，提高系统的可靠性且滑模抖振小。

本文基于含有功率扰动项的四阶电力系统模型，通过分岔图、Lyapunov指数谱和谱熵研究此模型中不同扰动参数改变时系统的非线性特性，发现功率扰动项可以使系统运动接近具有特定参数的周期轨道。此外，利用滑模控制进行混沌振荡的抑制，使得系统在控制过程中随时间变化，并且沿规定轨迹作小幅度的高频切换，以继电特性函数为切换面，使系统能够快速平滑地到达控制目标。数值仿真结果表明，该非线性控制器性能良好，使系统能够快速平稳地达到预期目标。

2 系统建模

同步发电机是电力系统最重要的能量来源，也是整个电网的核心。以同步电动机作为重要设备的互联电力系统的研究，是电力系统动态特性研究的关键。图1显示了带励磁环节的系统模型，这里的励磁环节是指发电机励磁系统控制回路，基本功能是为发电机励磁绕组提供直流电流（励磁电流），以形成发电机气隙磁场，实现转子机械能到定子电能的能量转换。

图 1中励磁控制器的输出电压Efd受控制器约束，依据输入电压Efdr的大小在有限区间内变动，系统方程可以描述为

其中，δ是发电机的功角，ω是发电机角频率，f0是同步电机基频，M是发电机转子的惯性，d是阻尼因子，Pm是输入功率的发电机，PG由发电机的电磁功率传递，x是输电线路的电抗，xd是发电机的电抗，xd′是发电机暂态电抗，Td′0是发电机定子绕组的时间常数，Efd是激励电压，V0是无穷大的电压，KA是放大增益，Vref是母线电压参考值，Efd0是励磁限制电压的参考值，V是发电机的终端电压，可表示为

电力系统中一般采用终端限幅方式的励磁环节对系统进行设备保护，励磁控制器的输出电压表示为

当输入电压Efdr在区间内时，输出电压 Efd=Efdr；当Efdr超出输出上限（或下限）时，输出电压Efd保持在上限而不再随Efdr变动，直到Efdr重新回到区间范围内。

结合电力系统实际操作参数和便于混沌研究，各系统参数取值如表1所示。

依据表1所给系统参数，可计算式（1）的耗散特性如式（4）所示。

表1 系统参数取值

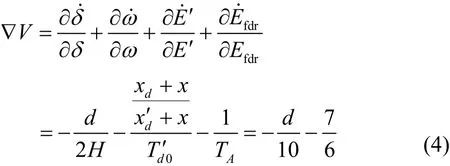
当系统阻尼系数为正时，∇V取值必为负，因此，只要保证电力系统等效阻尼一直为正阻尼，则式（1）表示的系统一定为耗散系统，对应t时刻的相空间体积V（t）在运动过程中总是不断收缩，如式（5）所示。当t→∞时，相空间体积为 0，系统运动轨迹收缩到有限范围内并最终固定在一个吸引域上，从而表明系统混沌吸引子存在的可能性。

为求取系统的平衡点，令式（1）左侧等于0，同时代入表1中的系统参数取值，可获得如式（6）所示代数方程。

其中，励磁控制器输出电压Efd表示为发电机端电压V表示为

为了更接近实际情况，在电力系统中考虑了不同的功率扰动，式（1）可以被描述为

3 功率扰动项对系统的影响

以电磁扰动的幅值eP和频率f1、负载扰动的幅值kP和频率f2，这4个电力系统参数为研究对象，采取单变量法，固定系统参数1.9229）作为系统初始值代入式（8）进行迭代运算。利用分岔图、Lyapunov指数谱和相图分别展示这4个参数对系统状态吸引子演变过程的影响。

3.1 电磁扰动幅值Pe

电磁扰动项的存在可能会使系统出现超高电压，影响系统的稳定运行，因此有必要对电磁扰动项进行研究。电力系统的振荡频率一般在0～2 Hz之间，选取Pk= 0，f2=0Hz和f1= 0.2 Hz，得到Pe∈ （0, 0.2255） 时系统的Pe分岔图和 Lyapunov指数谱，如图2所示。

图2 系统关于 eP的分岔图和Lyapunov指数谱

当Pe∈ （0,0.1256） 时，系统在参数范围内最大的2个Lyapunov指数（LE, Lyapunov exponent）同时保持趋近于0，即系统在该范围内LE值的分布情况为（0,0,-,-,-），通过 LE值并结合分岔图可判定系统运动在此范围内为拟周期态。而系统在拟周期态与混沌态的分界点Pe= 0.1256处的LE 具体值为 （0,0,-0 .094 4,-0 .250 2,-1 .1088） 。当Pe持续增大超过0.125 6后，系统的最大LE也会迅速增大并大于 0，系统运动实现由拟周期向混沌转变的过渡过程。在Pe∈ （0.1256,0.2255） 的范围内，对应图 2（a）和图 2 （b）的阴影部分，系统最大LE大于0，结合分岔图可知此时系统运行在混沌运动状态。当Pe＞ 0.2255时，由于式（8）中的电力系统不能长期处于稳定态，导致过度扰动作用下的电压崩溃。表2给出了部分Pe值时系统的LE和运行状态。

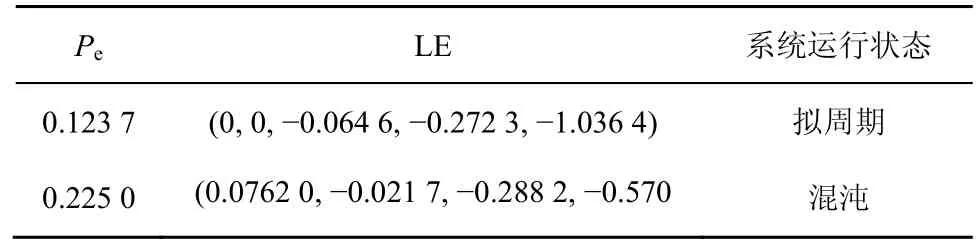
表2 不同Pe值时的LE与系统状态

3.2 电磁扰动频率f1

频率作为功率扰动的另一个重要参数，其取值也会直接影响到电力系统运动状态。在不考虑负荷扰动情况下，选取Pk= 0，f2=0和Pe= 0.02,得到f1∈ （0,2）时系统关于f1的分岔图和Lyapunov指数谱，如图3所示。

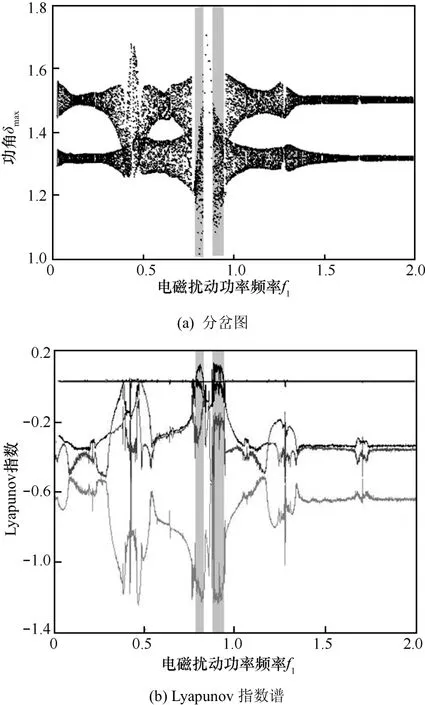
图3 系统关于 f1的分岔图和Lyapunov指数谱

在f1∈ （0.7780,0.8205）∪ （0.874 0,0.9315） 的范围内，即图 3（a）与图 3（b）中的 2块阴影区域，最大 LE大于 0，表明系统运动于混沌状态。当f1∈ （0.8205,0.9315） 时，对应图 3（a）与图 3（b）中 2块阴影区域的中间部分，该段范围内最大 LE等于0且次大LE小于0，即该参数范围内系统处于周期运动状态。而在f1∈ （0,0.7780）∪ （0.9315,2）时，系统的最大与次大LE均趋于0，从分岔图可看出此时系统处于拟周期运动状态。此外，f1= 0.420 0和f1= 1.2680的较小邻域内，最大的LE仍然为 0，次大 LE为负，在图4（a）中出现周期窗口。

图4 系统关于 f1特定值的相图

图4为f1=0.85和f1=0.90时系统的相图，可以明显看出系统运动状态从周期到混沌的变化，与上述分析相对应。部分f1值对应的系统LE和运行状态如表3所示。

3.3 负荷扰动幅值Pk

负荷扰动的存在可能会引起谐波和电压波动等损害电能质量的问题，威胁到电力系统的稳定，因此有必要对负荷扰动项进行研究。在不考虑电磁扰动情况下，选取Pe=0，f1=0，f2=0.2，得到Pk∈ （0,0.2555）时系统关于Pk的分岔图和 Lyapunov指数谱，如图5所示。

图5 系统关于 kP的分岔图和Lyapunov指数谱

在Pk∈ （0,0.137 0） 的范围内，系统最大 LE以及次大 LE均趋近于0，系统此时处于拟周期运动状态。当Pk∈ （0.137 0,0.205 5） 时，系统最大 LE保持 0，次大 LE≤0，系统运行在周期状态，且从图5（a）可看出周期数较大，而在上文中改变Pe时却并未找到周期运动的痕迹。当Pk∈（0.2055,0.2555）时，对应图 5（a）与图 5（b）中的阴影区域，该段参数范围内系统最大LE具有明显的正性，此时系统运动状态为典型的混沌态。而在Pk值超过 0.255 5时，系统将会因过大的扰动作用产生功角发散现象从而崩溃。表 4展示了部分Pk值时系统的 LE和运行状态。

表3 不同f1值时的LE与系统状态

表4 不同Pk值时的LE与系统状态

3.4 负荷扰动频率f2

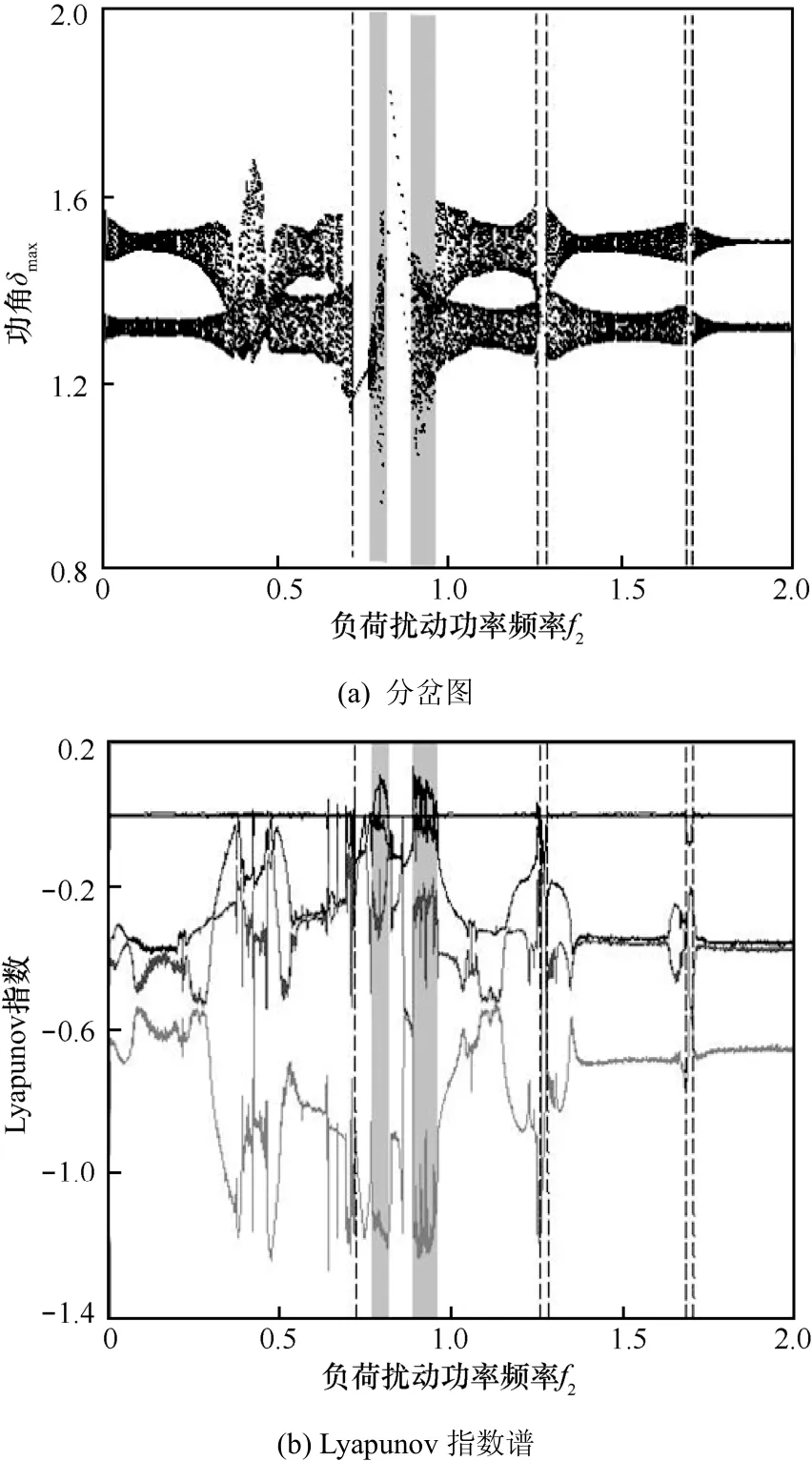
图6 系统关于 f2的分岔图和Lyapunov指数谱

与上文分析方法类似，在不考虑电磁扰动情况下，选取Pk= 0.02，Pe= 0，f1=0，得到f2∈ （0,2） 时系统关于f2的分岔图和Lyapunov指数谱，如图6所示。相较于改变f1时的情况，改变f2对系统带来的变化大体上相似，只存在几处较小的差别。当f2在（0.7615,0.8130 ）∪ （0. 8855,0.957 5） 的范围内时，对应于图6中2个阴影区域，此时系统的最大LE大于 0，说明系统运动状态为混沌态。当f2∈（ 0.7135,0.761 5）∪ （0.8130,0.8855）∪（1.2565,1.2775）∪（1.682 0,1.704 0）时，系统最大LE为0，其余的LE均明显小于 0，从图 8（a）对应区域也能观察到明显的周期窗口。当f2∈（ 0,0.7135）∪ （0.9575,1.2565）∪（1.277 5,1.682 0）∪ （1.704 0,2）时，系统中最大的2个LE值同时趋近于0，意味着系统在该参数范围内运行于拟周期状态。图7为f2=0.75和f2=0.90时系统的相图，可以明显看出系统运动状态从周期到混沌的改变，与上述分析相对应。部分f2值对应的系统LE和运行状态如表5所示。

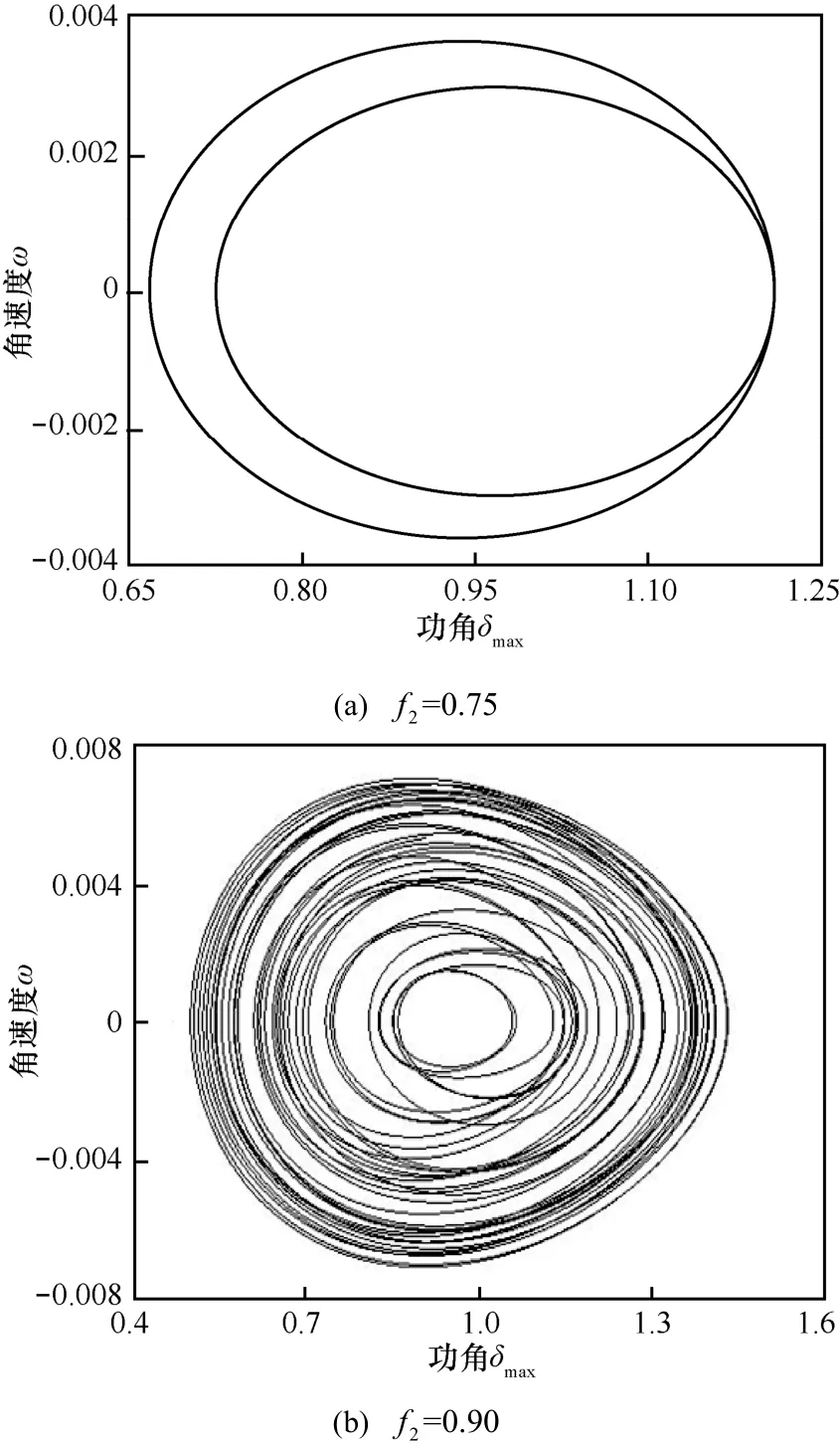
图7 系统关于 f2特定值的相图

4 系统的复杂度分析

混沌系统复杂度是指采用相关算法衡量混沌序列接近随机序列的程度，复杂度值越大，序列越接近随机序列，相应的运动越无规律[22]。对于电力系统而言，若其具有明显的振荡规律，则得到的SE测度值较小，即复杂度较小，若系统无振荡规律则复杂度较大。

为了进一步验证此模型的运动状态，这里引入谱熵复杂度（SE，spectral entropy）分析，图8为系统关于eP、kP、f1、f2的SE复杂度分析图。

由图8（a）与图8（b）可以明显看出系统随着eP和kP的增大，其复杂度呈现上升趋势，与系统从拟周期到混沌的运动轨迹相对应，在同一参数配置下，混沌运动的复杂度比拟周期和周期态大。图 8（c）与图 8（d）为系统关于f1和f2的SE复杂度分析图。图8（c）中虚线之间的区域对应于图 3（a）与图 3（b）中 2块阴影区域的中间部分，图 8（d）中虚线之间的区域对应在图 6（a）与图的范围内，这些部分均为系统出现小周期的区间，其 SE值较小，在混沌区间内，其SE值相对较大。不同于图 8（a）与图 8（b）中 SE 值呈现单调递增趋势，图 8（c）与图8（d）中的SE值变化起伏较多，即相比扰动幅值，在扰动频率影响下系统会展现出更加丰富的动力学行为。

表5 不同f2值时的LE与系统状态

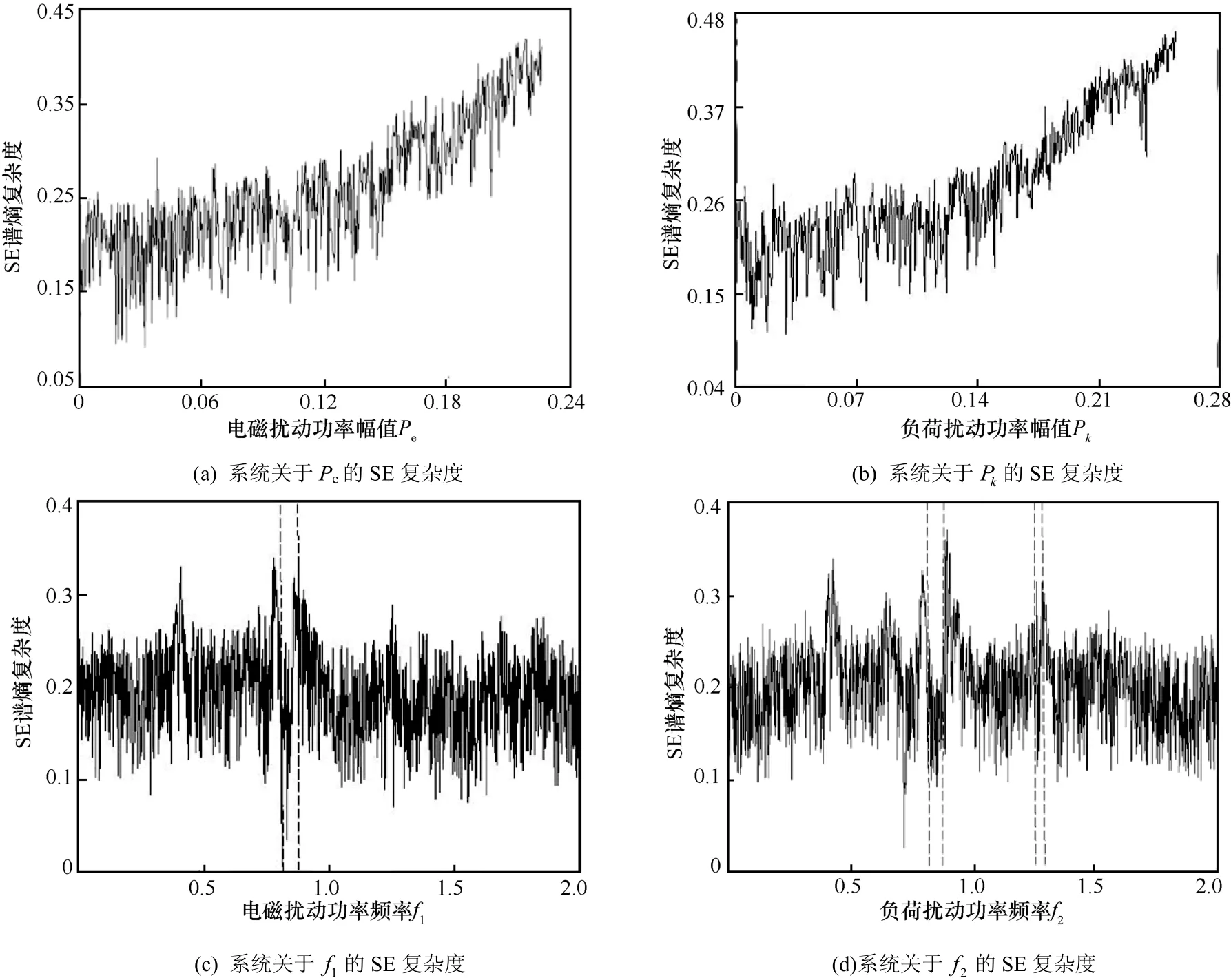
图8 系统关于 eP、 kP、 f1、 f2的复杂度

通过改变式（8）中的功率扰动参数，观察到了周期运动、拟周期运动以及混沌现象。与以往的工作相比，当功率扰动存在时，电力系统更有可能出现混沌振荡。因此，有必要设计一种有效的控制器来抑制电力系统的混沌现象。

5 混沌振荡的抑制

滑模控制器设计与系统参数无关，具有抗干扰能力强等特点。这里设计了一种基于低通滤波器的动态表面滑模控制方法，以抑制混沌振荡。该方法可以消除微分项的爆炸，具有简单的结构和参数设计，并将继电器特性函数作为控制器的开关函数，有效地抑制了系统的抖振。

5.1 控制器设计与稳定性分析

对于含功率扰动项的电力系统四阶模型式（8），以发电机功角δ作为控制目标，在方程组的第2项式加入控制律u，得到如下受控系统

设受控系统式（9）的预期控制目标为r，定义位置误差为

考虑到位置跟踪、虚拟控制和滤波误差，定义第二个Lyapunov函数为

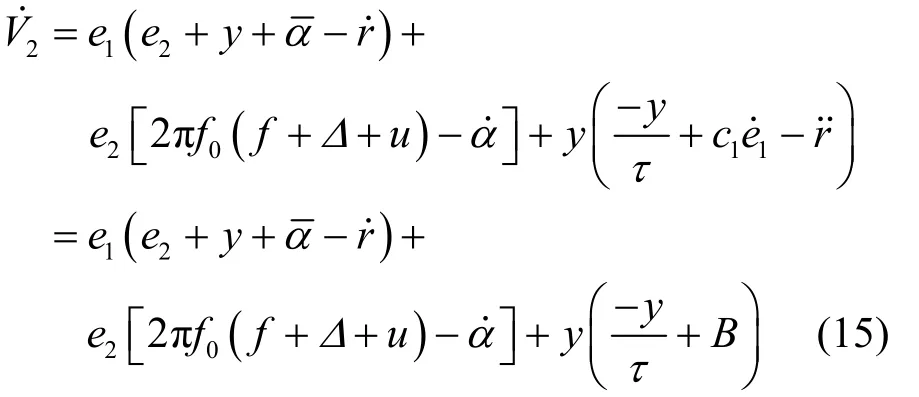
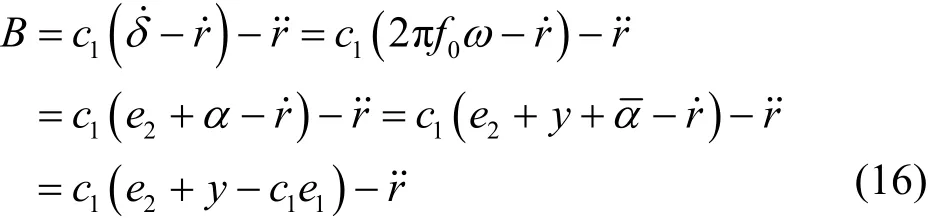
定义滑动面为 s=e2,则动态面滑模控制器设计为

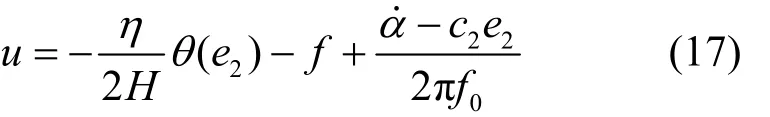
证明 当V2=p时B有界，记为M，则

得到

图9 目标轨迹为 r = 1.2 + 0.1sin（t） 的滑模控制

5.2 数值仿真

依据上文受控系统稳定性证明过程可知，χ越大控制效果越好，这也要求控制参数c1、c2尽可能取较大的正常数。此处选取控制器参数c1=c2=60，τ=0.01，η=0.3，ε= 0.001。选择2组不同的控制目标r= 1.2 + 0.1sin（t）和r=1.2，观察系统在控制器接入系统后的控制效果，结果如图 9和图 10所示。可以明显看出在控制器接入之前系统中功角δ非常不稳定，波动幅度大且没有规律性，在150 s加入控制器后功角δ趋于稳定，波动范围小且有规律，系统近乎没有抖振。

为体现本文控制方法的优越性，在相同参数条件下，采用符号函数即θ（s）= sgn（s）作为控制器的切换函数，并对相同的控制目标r= 1.2 + 0.1sin（t） 和r= 1.2进行追踪控制数值仿真，仿真结果如图 11和图12所示。显然，采用继电特性函数作为切换函数的控制器控制效果更好，系统平滑稳定无抖振。而采用常规的符号函数作为切换函数，虽然也能获得良好的控制效果，但系统抖振明显且抖振频率较高，同时也因剧烈的抖振现象导致数值仿真耗时长、数据量大。

图11 采用符号函数对目标轨迹为 r = 1.2 + 0.1sin（t） 的滑模控制

6 结束语

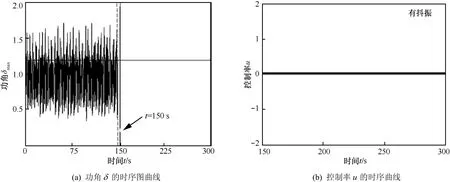
图12 采用符号函数对目标轨迹为r=1.2的滑模控制

本文建立了含有功率扰动项的四阶电力系统模型，基于耗散性分析了系统混沌吸引子存在的可能性，利用 Lyapunov指数谱、分岔图、相图、谱熵等研究了功率扰动项对系统运动状态的影响，可知在扰动频率影响下系统会展现出更加丰富的动力学行为。功率扰动项参数对系统功角影响更为敏感，随着扰动幅值到达某一值时，功角会急剧增大最终使系统失稳。本文根据系统特点设计了一种基于低通滤波器动态面滑模控制，选取继电特性函数作为切换函数，对电力系统中的混沌振荡进行抑制，理论和数值仿真结果都表明了该控制器具备良好的控制效果，能有效地去除抖振。