基于自抗扰的再入飞行器阻力加速度跟踪技术

霍斯琦，范世鹏，高 琦，贾静雅

(1.北京航天自动控制研究所， 北京 100854； 2.宇航智能控制技术国家级重点实验室， 北京 100854 3.首都航天机械公司， 北京 100076)

标称轨迹跟踪法是一种非常经典的再入制导方法，用来满足终端速度、终端高度、总航程的终端约束和热流、过载、动压等过程约束。然而，标称轨迹跟踪法对大气密度偏差、气动系数偏差等环境不确定性以及导航高度偏差[1]的适应性变差[2]，针对这一问题，有些学者提出可以先对各种不确定性进行辨识[3-5]，然后据此对标称轨迹对应的标称控制量以及跟踪反馈控制律参数进行修正。另有一些非主流的方法，如文献[6]基于自适应补偿思想，通过加入一个标称控制修正量使各种不确定因素下弹道跟踪误差收敛速度与标称情况相同；文献[7]通过分析再入初始高度偏差和气动系数偏差对动压影响，提出根据初始高度调整制导指令和根据下沉率进行过载指令补偿的闭环制导方法。

随着自抗扰控制技术的发展，强适应性跟踪律设计问题有了新的解决思路，即可以将这类制导问题转化成存在扰动的线性系统控制问题，通过不加区分的将各种偏差综合影响视作飞行控制系统中的扰动，利用扩张观测器对其进行观测并在原有制导律中进行动态补偿[8]，来提高制导律的适应性。文献[9]应用微分平坦原理将飞行器纵向质心运动模型转化为两个二阶线性定常积分链系统，并基于自抗扰思想对大气密度、气动系数偏差带来的影响进行补偿，但是以质心运动方程形式表示的标称轨迹的设计和存储所需保障较为复杂，且该方法并不适应于存在导航高度偏差情况；文献[10]对平衡滑翔飞行器设计自抗扰跟踪律跟踪阻力-能量剖面(D-E剖面)，得到速度滚转角控制指令，然而这里的扰动是指阻力加速度控制模型中的强时变非线性动态部分，与环境不确定性与导航高度偏差对模型的影响无关；文献[11]针对平衡滑翔飞行器再入模型参数不确定问题，根据自抗扰控制方法对参数拉偏不敏感的特性设计阻力加速度跟踪律，但该方法仍需对阻力加速度控制模型中非线性动态部分求导，前期推导工作较复杂，且控制参数的选取没有给出明确说明，亦没有对导航高度偏差问题进行讨论。

本文基于自抗扰控制理论，设计阻力-能量剖面的强适应性跟踪律，做到在存在各种环境不确定性和导航高度偏差条件下，跟踪效果良好，并通过数学仿真，验证了本文算法的有效性。

1 模型建立

不考虑地球扁率及地球自转的影响，高超声速STT飞行器在纵向平面内的三自由度无量纲动力学方程为：

(1)

其中：

(2)

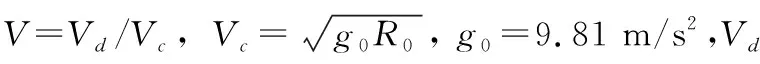
本文采用的再入制导策略是使飞行器定总攻角飞行，通过控制攻角来控制纵向加速度分量，从而控制高度，最终达到控制阻力加速度，使其跟踪标称阻力剖面的效果。控制量为升力加速度(唯一取决于攻角)的阻力加速度控制模型为[10]：

(3)

其中，uL,D、L分别为简写，D′为D对τ的导数。

2 D-E剖面的强适应性跟踪律设计

在标称剖面给定的前提下，跟踪律的设计问题即为跟踪误差状态空间的有限时间镇定问题。首先可根据标称剖面推算阻力加速度状态空间中控制量及各状态量的参考值，得到：

(4)

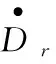
那么wr为参考干扰，表达式为

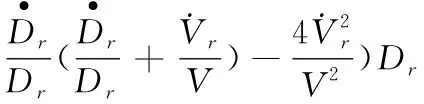
(5)

而实际弹道的阻力加速度状态空间也可以表示成相似的形式

(6)

这里干扰量w由两部分组成，前一部分w1可看作系统内扰，代表阻力加速度控制模型自身所包含的时变强非线性动态，而后一部分w2则看作系统外扰，代表气动偏差(阻力系数偏差、大气密度偏差)和导航高度偏差对阻力加速度控制模型的影响。

(7)

w2的产生可理解为当考虑气动偏差(阻力系数偏差、大气密度偏差)和导航高度偏差时，相同的指令攻角αc对应的控制量由u变为u′所带来的附加控制作用，如果在设计控制量u时考虑各种环境不确定性和导航高度偏差导致的附加控制作用，并在设计控制律时主动将其补偿抵消掉，那么就可以认为这种新型的控制律对各种环境不确定性和导航高度偏差不敏感，具有较强适应性。

式(6)与式(4)相减可得到跟踪误差状态空间：

(8)

其中Δ(·)代表各状态量、控制量、干扰量实际值与参考值的偏差。在状态偏差量、干扰偏差量已知的前提下，则可以进行状态反馈律设计与动态补偿使跟踪误差状态在有限时间内收敛至近乎为零，完成D-E剖面跟踪。跟踪律设计为

(9)

将式(9)代入式(8)得：

(10)

可见这里通过状态反馈与动态补偿将系统极点配置为双重负实根，保证了跟踪误差状态镇定，唯一需要设计的极点位置γgz与跟踪速度直接相关，决定跟踪性能。实际控制量u=ur+Δu随之可算得，而指令攻角αc可根据标准大气密度、未拉偏气动参数和惯组输出导航高度由u反推。根据定义：

(11)

则反推得到：

(12)

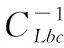
然而各状态偏差量、干扰偏差量的获得需要对系统式(6)中各状态量，干扰量进行观测，这便需要构建扩张状态观测器(ESO)。跟踪律的实现需要状态观测与动态补偿，从而达到重构被控对象的目的，得到想要的动态性能，满足自抗扰控制的核心思想。可以说，将自抗扰思想用于阻力加速度跟踪设计，可以提高该跟踪律对环境不确定性和导航高度偏差的适应性。

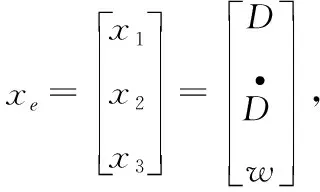
(13)

其中

对xe构建扩张观测器1

(14)

则式(14)与式(13)作差得：

(15)

那么在(A1,C1)可观，(A1,B2)可控的前提下，可以对e构建扩张观测器2进行观测，并以观测量设计状态反馈使e在有限时间内收敛至指定精度范围，从而保证扩张观测器1的性能。构建的扩张观测器2如下：

(16)

而反馈控制律为u0=Ckξ。合理选择参数γ使得：

λi(A1+B2Ck)=-γ

λi(A1-BkC1)=-γ(i=1,2,3),(γ≻1)

(17)

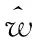
3 仿真分析

本文的研究对象为某低空飞行的STT飞行器，较之平衡滑翔飞行器，其机动距离更短，减速范围更小。标称剖面在此直接给出，为一条位于再入走廊内且满足终端速度、高度约束及航程约束的给定剖面。ESO的唯一设计参数γ取8.5×tscale，跟踪律的唯一设计参数γgz取0.3×tscale，tscale为上文提到的时间归一化因子，a1固定为-12.5。

可见观测器开启及控制律切换时，各阶观测输出都会有不同幅度的动态过程，阶数越高，幅度越大，但均在有限时间内趋于稳定，较好跟踪实际值。

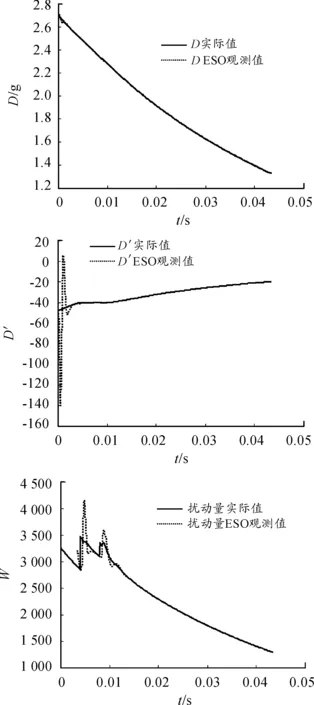
图1 ESO观测情况

图2为有干扰偏差补偿和无干扰偏差补偿时两跟踪误差状态随时间变化的曲线，即标称弹道跟踪情况。

存在干扰偏差补偿时，阻力加速度跟踪误差在28 s之后恒为零，说明本文讨论的跟踪控制指令算法不仅对大气密度、气动系数偏差有强适应性，而且最终达到的跟踪效果良好；而缺少干扰偏差补偿时,阻力加速度跟踪误差始终无法归零，说明剖面跟踪性能较差，影响打击终端航程约束。

图3为大气密度、气动系数均拉偏20%和均拉偏-20%两种情况下实际控制量变化情况。当跟踪误差状态归零后，可以看到，实际控制量与标称控制量不等，负极性拉偏时的比标称控制量大，正极性拉偏时的比标称控制量小。原因在于负极性拉偏时，产生同样控制作用所需攻角更大，则根据实际控制量定义，由攻角、标称大气密度、未拉偏气动系数求得的实际控制量会变大，正极性拉偏情况同理。该现象恰证明本文的跟踪控制指令算法会根据实际大气密度、气动系数进行调整，凸显其对环境不确定性的强适应性。

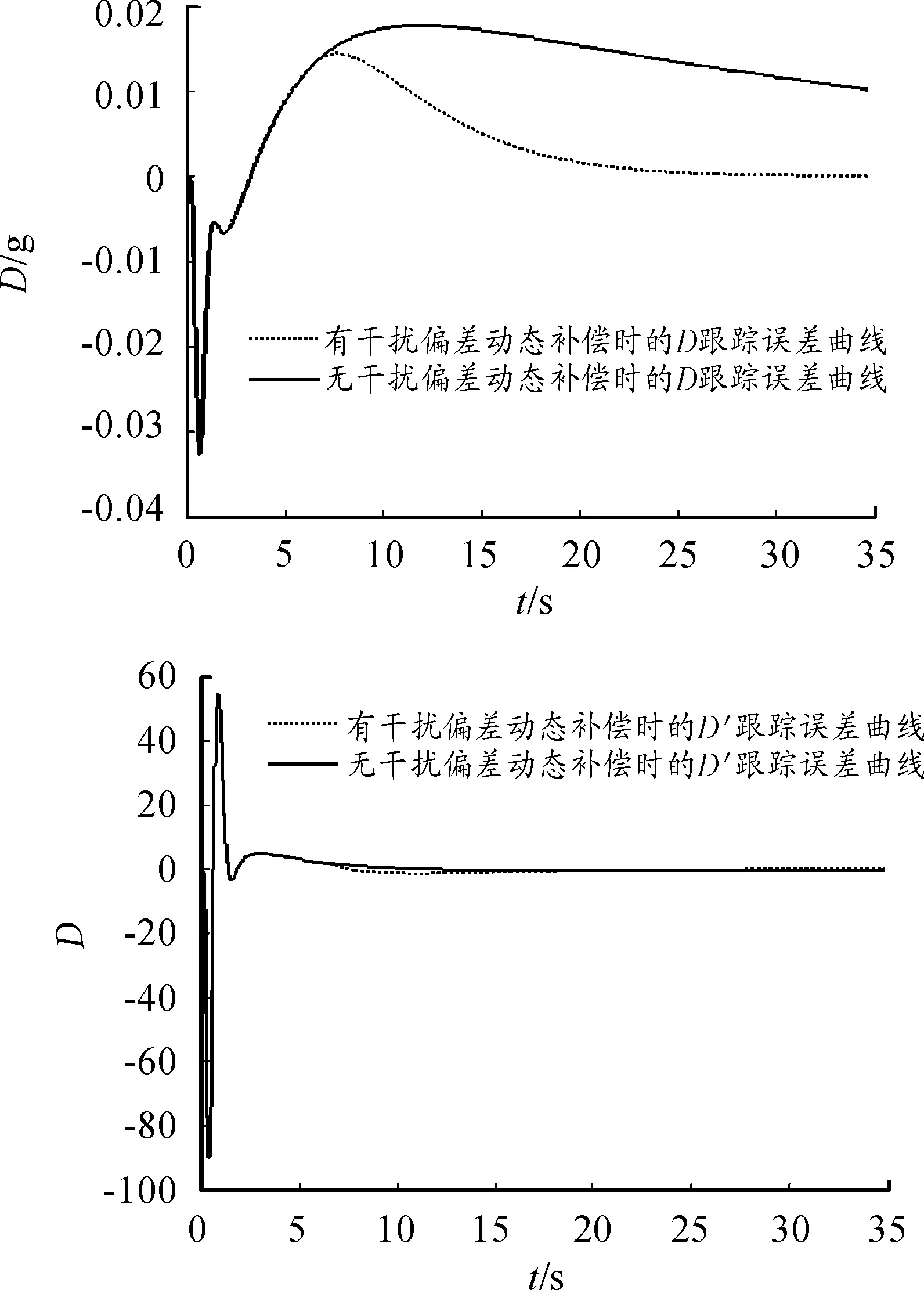
图2 跟踪误差时间曲线

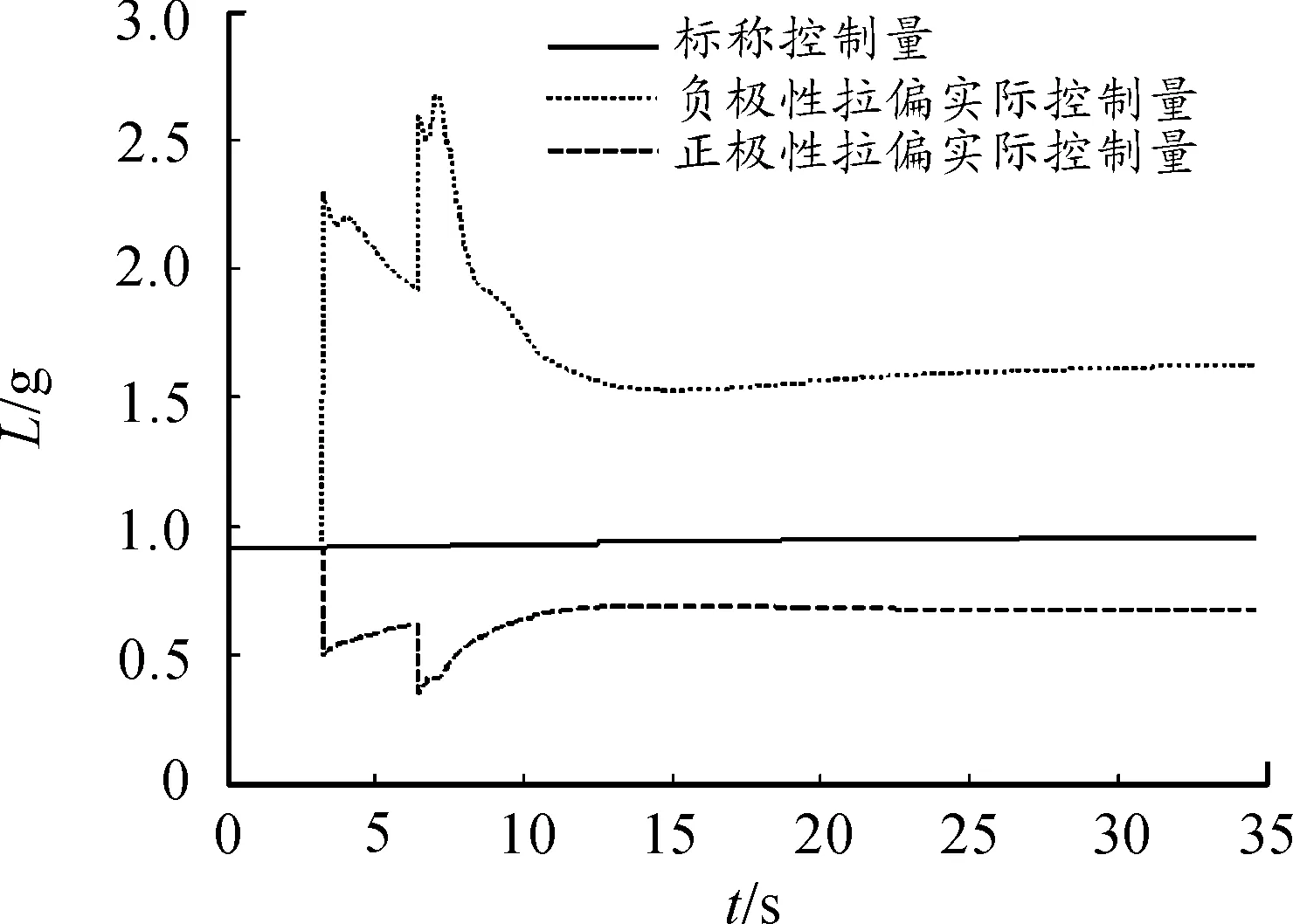
图3 正/负极性拉偏时控制量的时间曲线

考虑导航高度偏差影响，当大气密度、气动系数均拉偏20%且存在3 km导航高度偏差(惯组输出高度值总是比飞行实际高度高3 km)时，跟踪律效果及控制量曲线如图4，图5可见，跟踪效果良好且控制量正常。

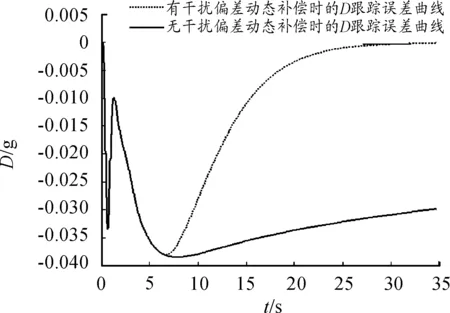
图4 存在导航高度偏差时跟踪误差曲线

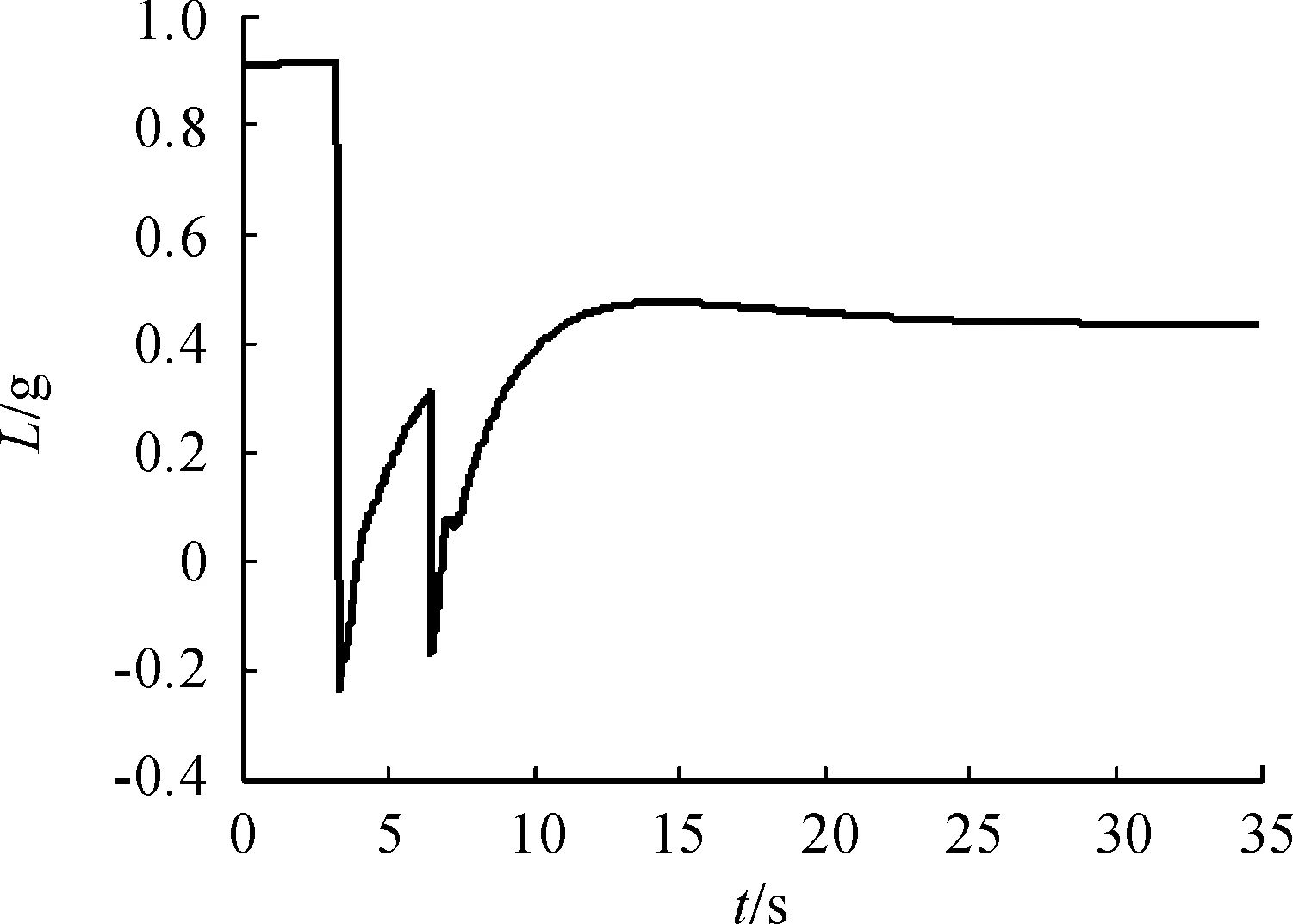
图5 存在导航高度偏差时控制量曲线

4 结论

仿真结果表明，在存在大气密度、气动系数、导航高度偏差条件下，该跟踪律跟踪效果良好且参数设计简单，不需要系统提供阻力加速度微分信息，又可以根据标称大气密度气动参数和存在偏差的导航高度直接反解实际攻角指令，具有一定的工程应用价值。