基于蒙特卡洛法的武器系统标定误差分析

谢瑞煜，赵建军，蒋 涛

(1.海军航空大学， 山东 烟台 264001; 2.中国人民解放军91912部队， 福建 宁德 352000)

按照战术技术的要求，武器系统在阵地部署时，必须先进行标定。由于地面作战系统的各设备在阵地上是分散布置的，为完成各车间的目标坐标的传输、变换和修正等，作战装备间应进行方位、距离和高度差的标定，即确定各车之间的相对距离、相对方位角度和相对高度差。

传统的标定方法是采用激光测距仪测出相对距离，瞄准望远镜加数字罗盘测相对方位角。该方法易受到环境的制约，视线遮挡等限制。为了克服这些缺点，本文采用陀螺仪[1-2]测载体与正北夹角，北斗定位系统(BDS)[3-4]测相对方位角、相对距离和高度差的新方法[5]。在实际标定过程中，由于各种测量手段存在不同程度的误差，这些误差会不断积累[6-9]，会使得武器系统打击精度下降，影响战斗力。作为一种随机抽样方法，它是通过计算机来产生满足要求的随机测量数据来取代实际测量，在产生大样本的同时减少了工作量，提高了测量可信度中难以得到的数据，从而解决存在的问题。

1 标定误差分析建模

1.1 相对方位角的标定

1.1.1 相对方位角的标定分析

相对方位角标定是通过两载体获得各自北斗定位数据进行计算得到的，具体过程如下：

通过车载差分BDS定位，可以求得载体定位值，即各车的经纬度高程，将定位的两个载体设为A载体和B载体。

设载体A为当前位置，载体B为目标位置，B与A的连线与正北的夹角即为方位角。Aj为A点经度；Aw为A点纬度；Bj为B点经度；Bw为B点纬度。

北纬为正，南纬为负；东经为正，西经为负；经纬度单位使用度。R为地球平均半径；Azimuth：方位角。

图1中A，B，C即表示点，又表示球面上“弧线”在这些点的夹角；a，b，c表示A，B，C三点的对“弧”两端点与地心连线所夹的角；O为球心；L为AB两点间球面距离。

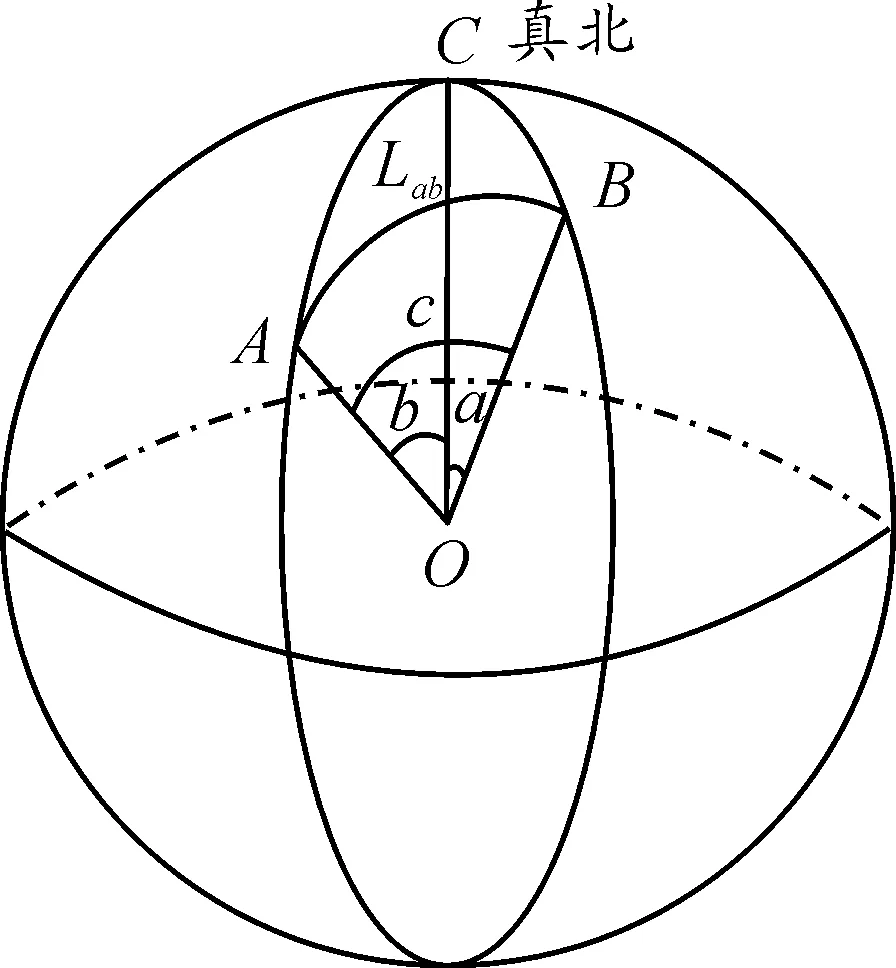
图1 球面示意图

首先需要用到三面角余弦公式：

cos(c)=cos(a)×cos(b)+sin(a)×sin(b)×

cos(A-OC-B)

(1)

式(1)中,A-OC-B是面AOC与面BOC的二面角，即两点经度之差。

将已算得AB点经纬度代入式(1)，得：

cos(c)=cos(90-Bw)×cos(90-Aw)+

sin(90-Bw)×sin(90-Aw)×cos(Bj-Aj)

(2)

将角c的余弦值转换成正弦值，得：

(3)

将角c转换成角a,需要用到球面正弦公式：

(4)

将式(3)代入式(4)，得：

(5)

需要注意的是：式(5)计算得到的方位角数据有时与方位角的定义不一致，因此要根据相应位置进行讨论处理。假设A点固定于原点，则：

B点在第一象限，Azimuth=A；

B点在第二象限，Azimuth=360+A；

B点在第四象限，Azimuth=180-A。

1.1.2 相对方位角的标定误差源分析

在这个过程中，所测得的数据中存在误差。首先BDS定位数据受到卫星部分、信号传播部分以及接收机部分的影响，每一部分中，比如钟差、电离层对流层折射、多径效应等都会影响定位的精度。同时接收机的安装位置也会影响，在实际安装时，接收机不可能安装在载体的中心位置，而计算相对距离或方位角都将车体的中心作为计算点，因此在误差计算时，需要将安装偏差转换到经纬度高程中，具体过程如下：

首先建立载体坐标系，在以车体的中心为原点，水平纵向为x轴，水平横向为y轴，垂直车体为z轴，设接收机的坐标点为[xbybzb]，通过载体坐标系到地理坐标系的转换公式，得到地理坐标系上的点。

[xnynzn]T=[cosθcosθ1]-1·[xbybzb]T

(6)

式(6)中，[xnynzn]T是转换到地理坐标系上的坐标θ为载体纵向与正北的夹角，即寻北仪的寻北值，这也是标定中的一项误差源。

然后转换到大地直角坐标系，有：

(7)

(8)

式(7)中[xgygzg]T是转换到大地直角坐标系上的坐标；式(8)中J0、W0是地理坐标系坐标原点的经纬度。

接着转换到大地直角坐标系，有：

(9)

式(9)中，J′为经度值误差；W′为纬度值误差；H′为高程误差；R为地球半径。

1.2 相对距离和高度差的标定

经过1.1节的计算，其中式(2)的结果先经过反余弦函数计算得c的度数，再利用角度到弧度的计算公式，化为弧度值，最后与地球半径的乘积就是AB两点间的球面距离，公式为：

c=arccos(cos(90-Bw)×cos(90-Aw)+

sin(90-Bw)×sin(90-Aw)×cos(Bj-Aj))

(10)

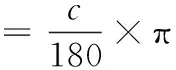
(11)

L=R×c(弧度)

(12)

式(12)中，L为相对距离。

将式(10)、式(11)代入式(12)得到相对距离值。

相对距离标定的误差源分析与方位角的类似，这里不再赘述。

高度差即为BDS定位数据中的高程值之差：

H=|HB-HA|

(13)

式(13)中，HA、HB为载体A、B的高程值。

其误差源为定位误差和接收机安装位置偏差，根据式(13)，右边为定位的高程值，高程值误差直接导致高度差产生误差；同时接收机的安装位置偏差属于系统误差，导致接收机的高程值产生系统误差，从而影响高程差。

2 基于蒙特卡洛法的标定误差处理

蒙特卡洛法基于伯努利定理及大数定理，在使用其解决问题时，需要通过以下步骤进行：

步骤1 建立该问题的数学模型。

步骤2 按照概率分布进行随机变量抽取。

步骤3 通过反复抽取的模拟实验，对获取的数据进行统计、分析，最终得到问题答案。

在分析标定误差时，需要知道影响最后标定结果的各个测量值，建立误差模型为：

ΔY=G(x1+Δx1,x2+Δx2,…,

xn+Δxn)-G(x1,x2,…,xn)

(14)

式(14)中，xi为标定步骤中的各参数真实值；Δxi为各参数的误差；G为标定计算过程。

设标定求解过程为：

[L,A,H]=G(X)

(15)

式(15)中，L、A、H分别为相对距离、相对方位角和高度差。

则标定误差模型为：

[ΔL,ΔA,ΔH]=G(X+ΔX)-G(X)

(16)

式(16)中，ΔL、ΔA、ΔH为各自的误差。

标定误差计算流程如图2所示。

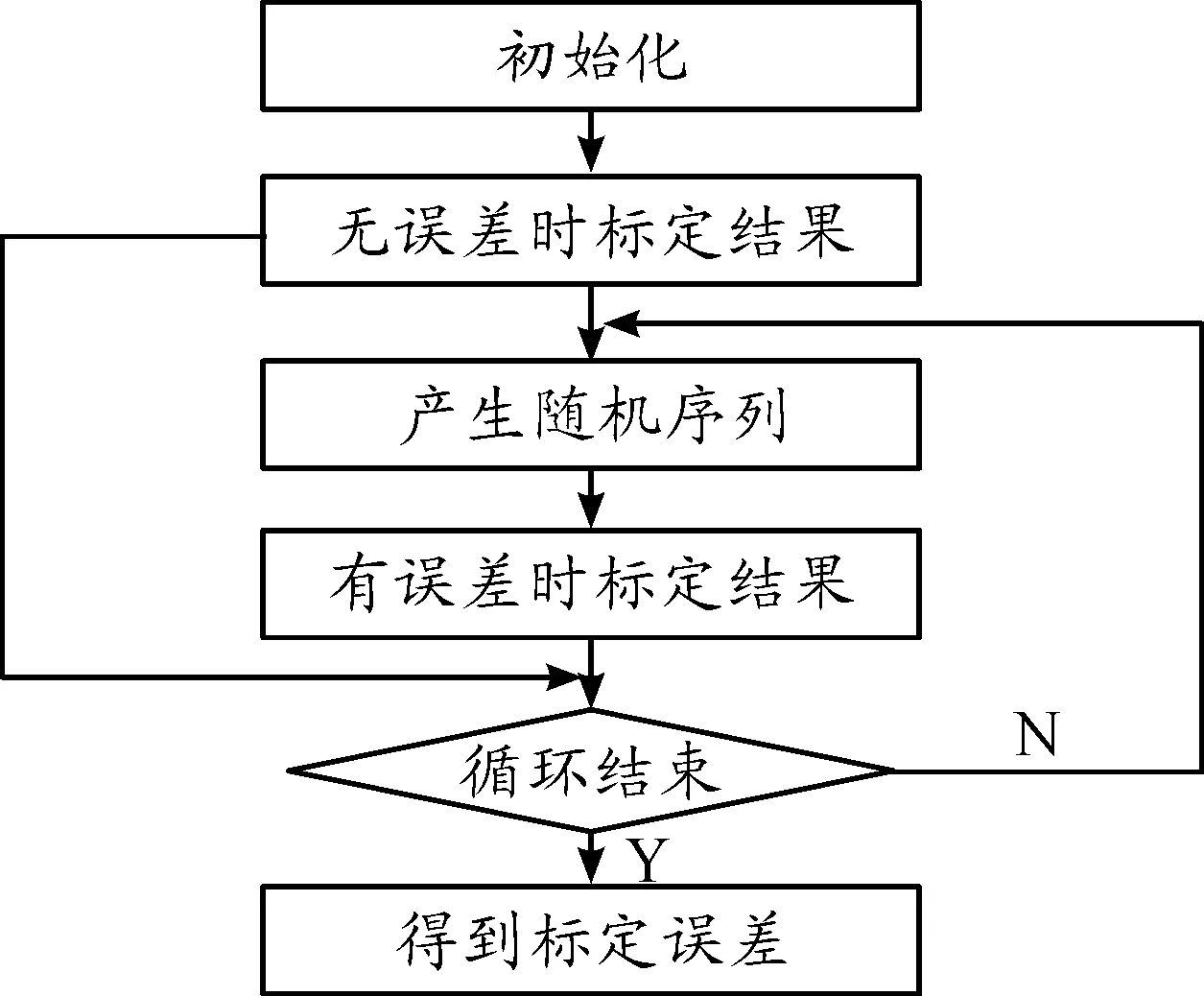
图2 标定误差流程

3 仿真与分析

3.1 测量及标定结果的仿真

根据实际情况，武器系统在标定过程中涉及到的误差源设定如表1所示。设定载体B与载体A同型号，安装的接收机与寻北仪相同，载体A、B接受机和寻北仪误差相同。设定载体A大地坐标系中的定位坐标为(110,20,10)，寻北值为30°；载体B定位坐标为(110.01,20.01,13)，寻北值为32°。根据表1中各个参数的概率形态生成随机序列长度为1 000随机序列。

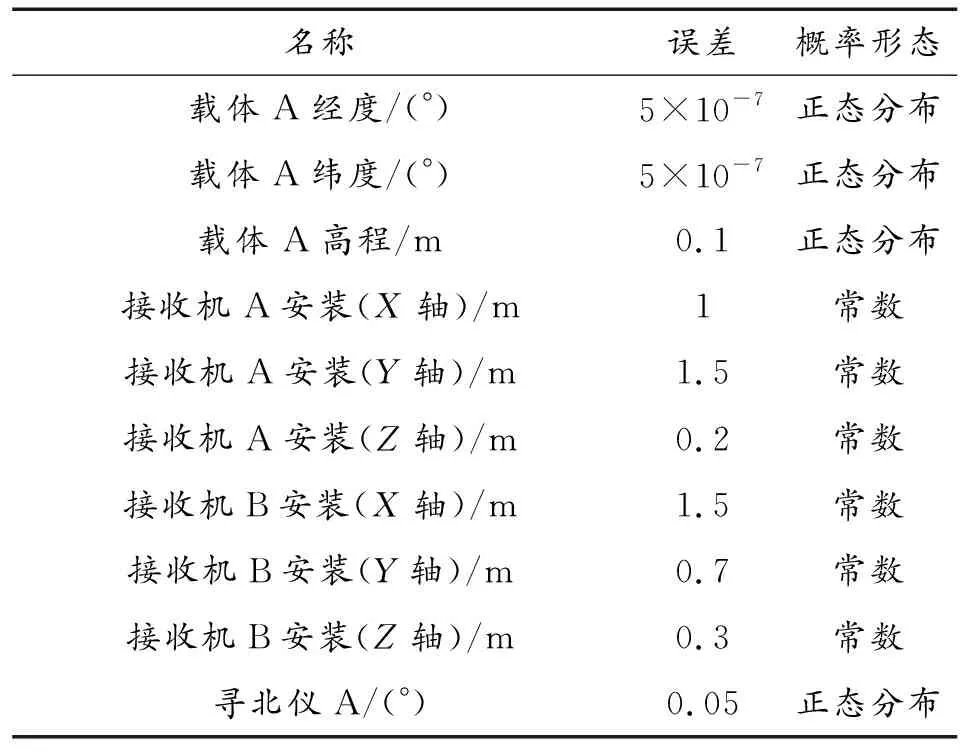
表1 仿真计算采用的数据

通过仿真计算，得到基于蒙特卡洛法的1 000次测量值分布图如图3所示。

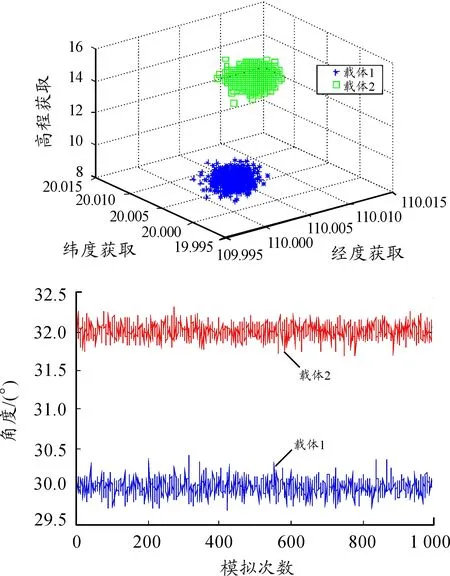
图3 车载接收机和寻北仪测量值

根据标定模型计算得到相应的标定值，即相对方位角、相对距离和高度差。如图4所示。

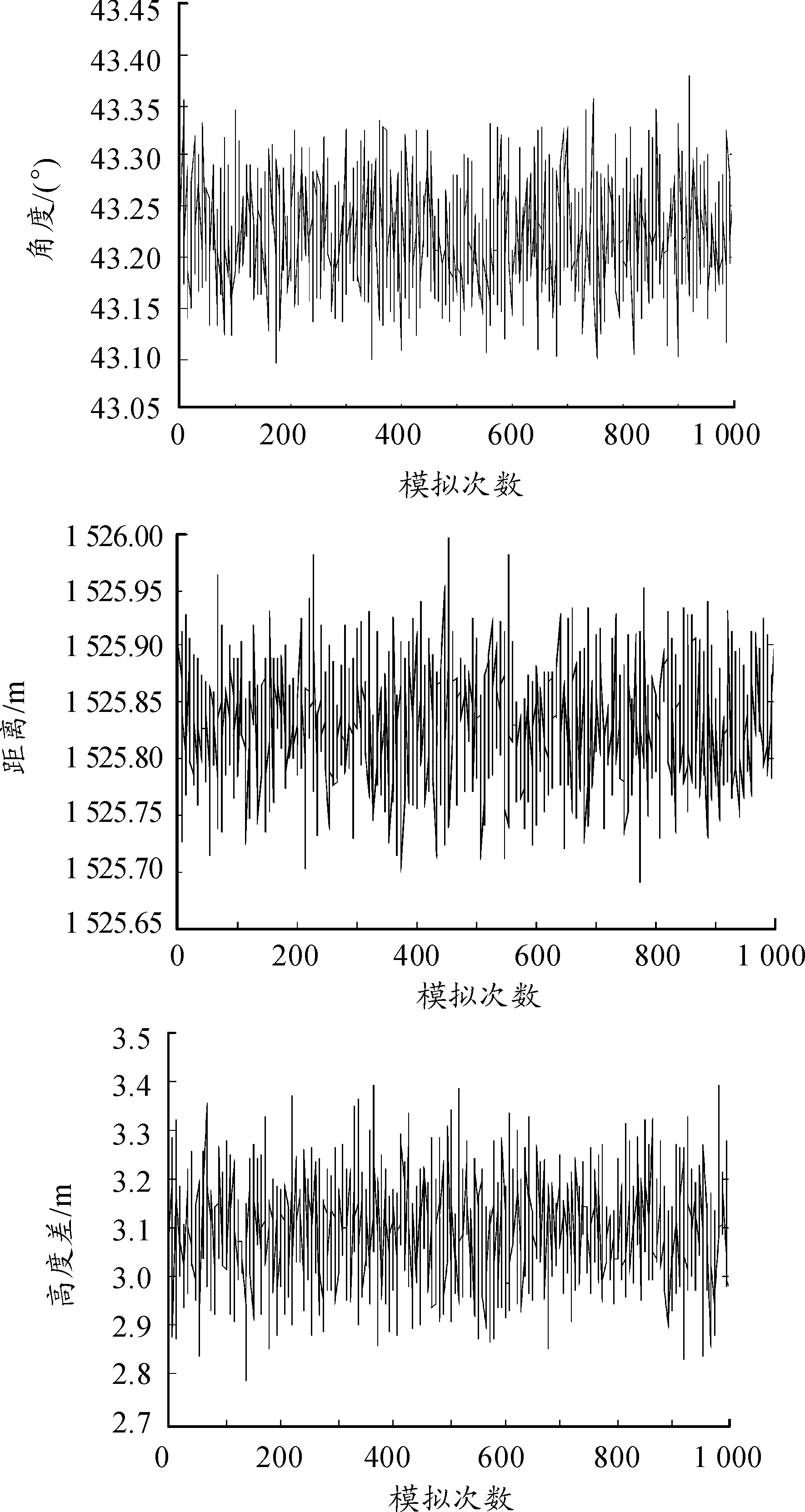
图4 相对方位角、相对距离和高度差

由图4可以看出，相对方位角、相对距离和高度差的误差服从于μ=0的正态分布，相对方位角误差在-0.16°～0.18°之间，相对距离误差在-0.14～0.17 m之间，高度差误差在-0.32～0.39 m之间。

3.2 各部分误差和偏差对标定结果影响的仿真

1) 接收机信号误差对标定误差的影响

接收机信号误差对标定误差的影响图图5、6所示。

图5、6中显示接收机接收的经纬度误差从-1×10-6度增加到1×10-6度，高程误差从-0.2 m到0.2 m，标定误差的变化。随着接收机的经纬度误差的增大，标定的误差绝对值呈上升趋势。在方位角标定中，经度是正相关，误差平均上升1×10-7度，方位角误差增加3×10-4度；纬度是负相关，误差平均上升1×10-7度，方位角误差绝对值增加3×10-4度。在距离标定时，经度误差平均上升1×10-7度，距离误差增加7.2×10-3m；纬度误差平均上升1×10-7度，距离误差绝对值增加8.2×10-3m；高程误差的影响小于定位随机误差，出现散点，可以忽略不计。在高度差标定时，高程误差平均上升0.02 m，高度差误差增加0.2 m。

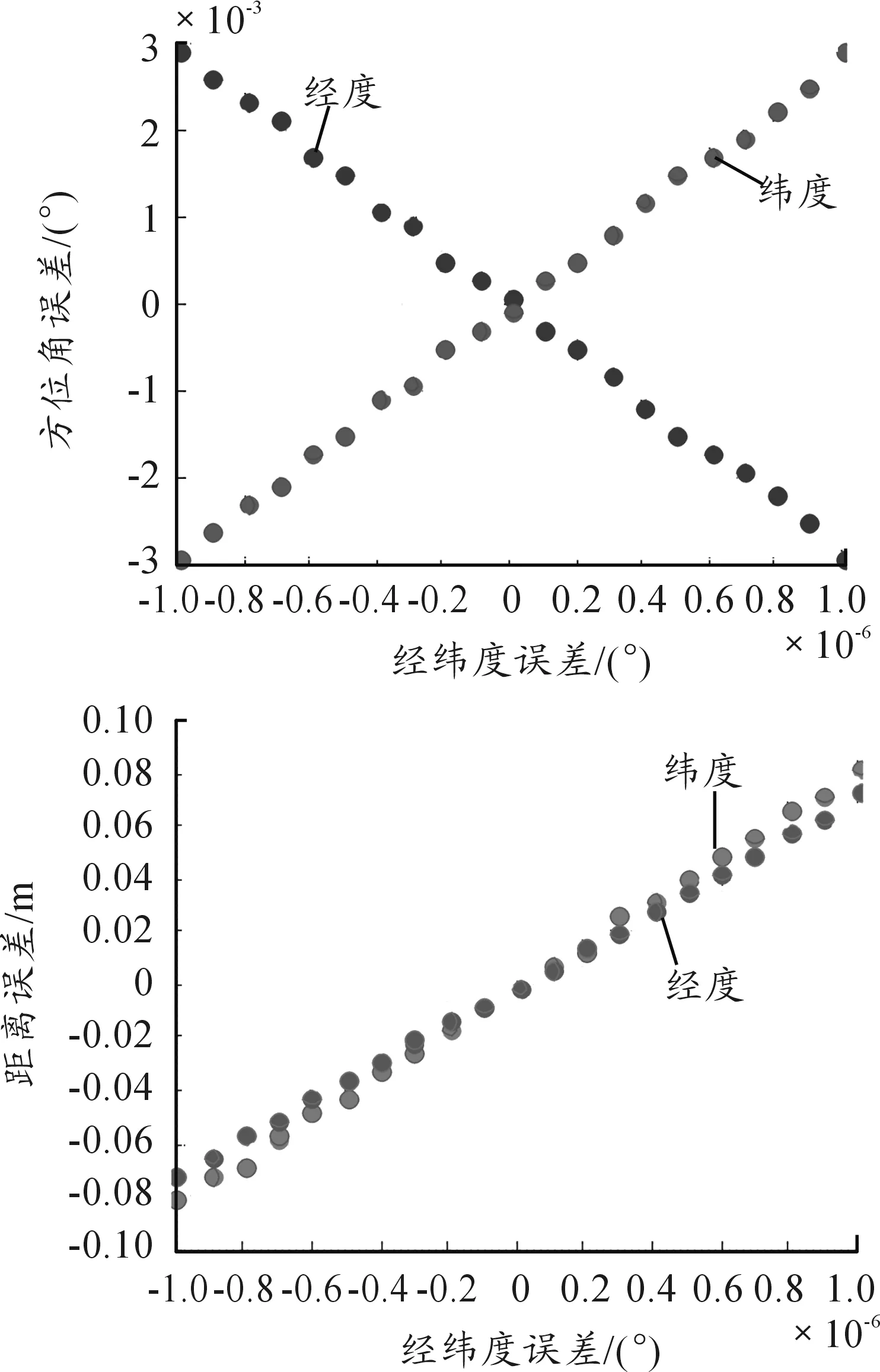
图5 经纬度误差对方位角和距离的影响

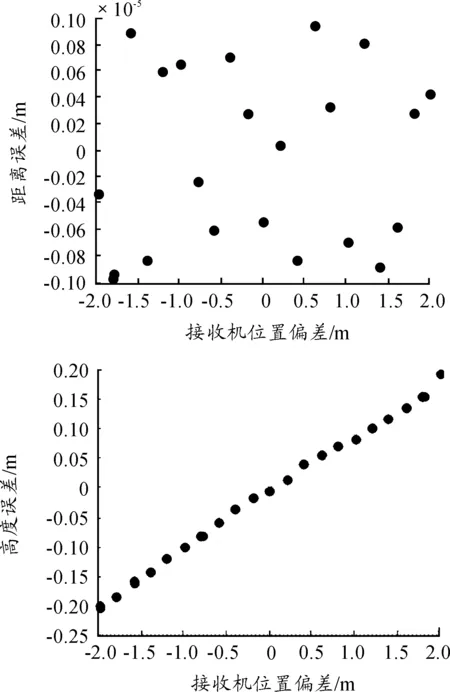
图6 高程误差对距离和高度角的影响

2) 接收机安装位置偏差对标定误差的影响

接收机安装位置偏差对标定误差的影响如图7所示。

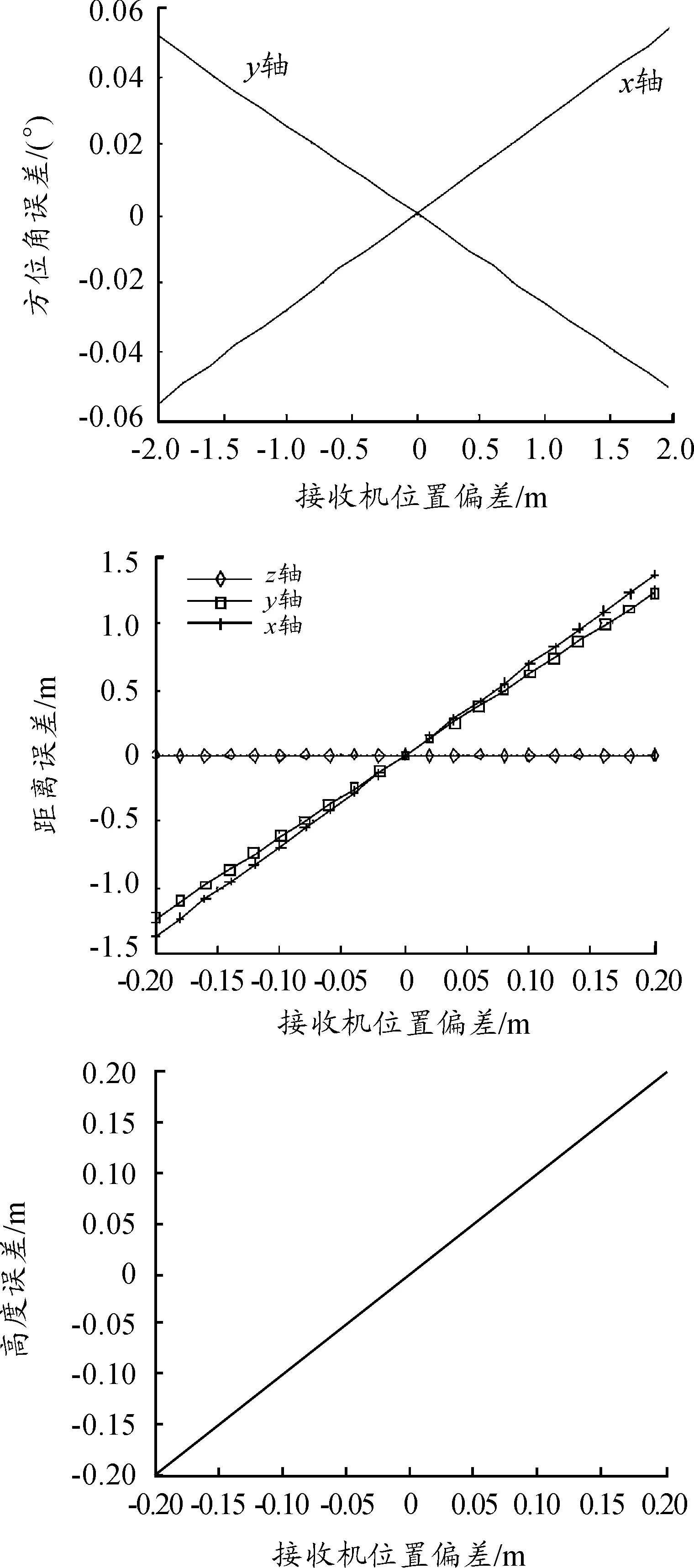
图7 接收机位置偏差对方位角、距离和高度差的影响

图7中显示接收机安装位置x轴、y轴和z轴偏差从 -2 m增加到2 m，标定误差的变化。随着接收机安装位置偏差的增大，标定的误差绝对值呈上升趋势。在方位角标定中x轴是正相关，偏差平均上升0.2 m，方位角误差增加5.5×10-3度；y轴是负相关，偏差平均上升0.2 m，方位角误差绝对值增加5.1×10-3度。在距离标定时，x轴偏差平均上升0.2 m，距离误差增加0.137 m；y轴偏差平均上升0.2 m，距离误差减小0.125 m；z轴偏差平均上升0.2 m，误差可以忽略不计。在高度差标定时，只有z轴偏差有影响，偏差平均上升0.2 m，高度差误差增加0.2 m。

3) 寻北仪误差对标定误差的影响

寻北仪误差对标定误差的影响如图8所示。

图8中显示寻北仪误差从-0.2°增加到0.2°，标定误差的变化。随着寻北仪误差的增大，标定的误差绝对值呈上升趋势。在方位角标定中，寻北仪的误差是负相关，误差平均上升0.02°，方位角误差绝对值增加1×10-5度。在距离标定时，寻北仪误差的影响小于定随机误差，出现散点，可以忽略不计。

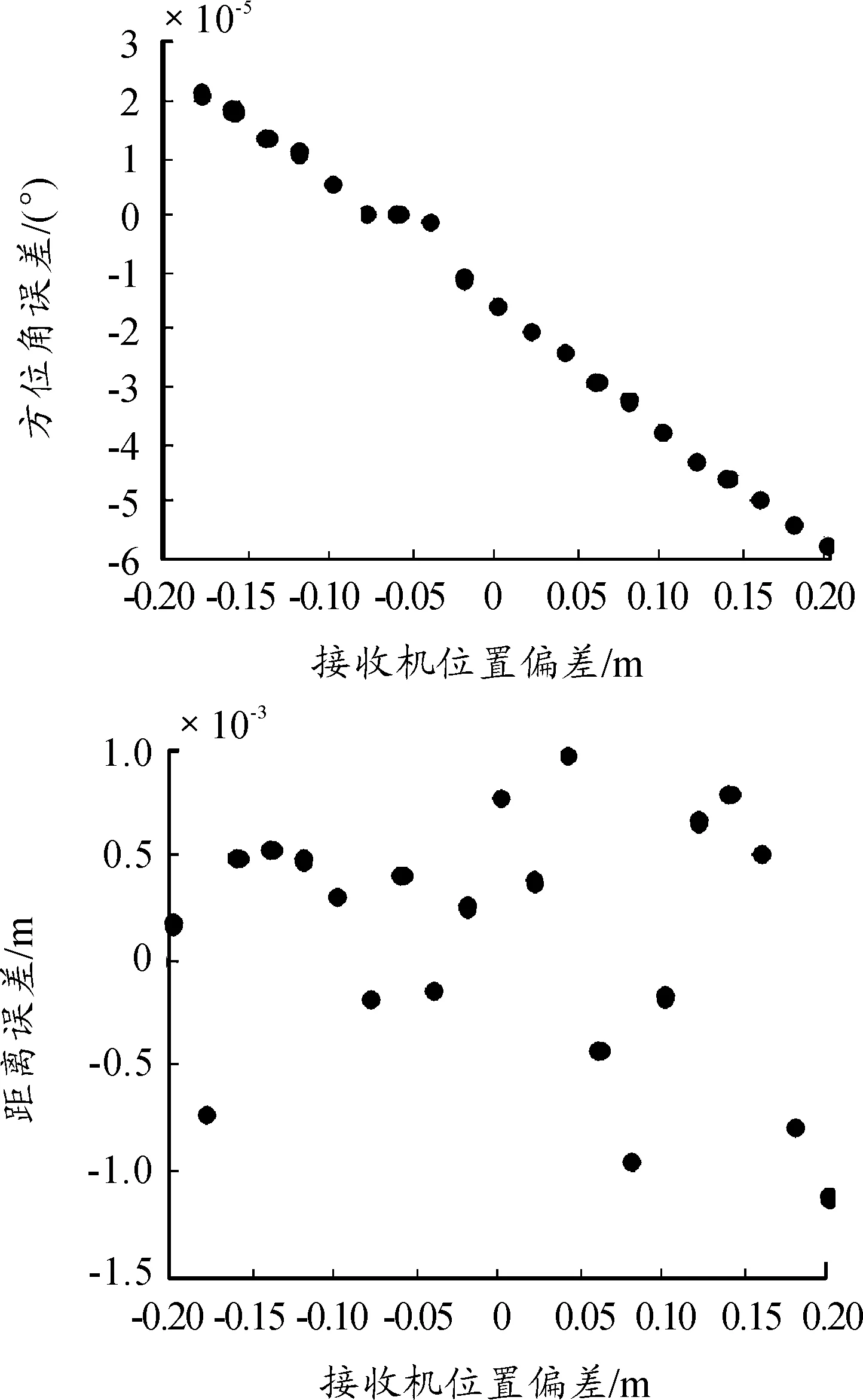
图8 寻北仪误差对方位角和距离的影响

按照上述的仿真结果，寻北仪的误差可以忽略不计。将测量误差的范围统一到米级,经纬度误差范围为-1×10-5度到1×10-5度(1×10-5度的误差距离为1 m左右)，经、纬度误差导致的方位角误差为0.03°，接收机x、y轴安装位置偏差则为0.027 5°；经、纬度导致的距离误差为0.72 m，接收机x、y轴安装位置偏差则为0.685 m；高程误差与接收机z轴安装位置偏差都为1 m。因此影响相对方位角和相对距离的主要因素是经纬度误差和接收机x、y轴安装位置，但前者影响均稍大于后者；而高程和接收机z轴安装位置影响高度差相同。

4 结论

1) 采用陀螺仪加卫星定位进行标定的方法能有效降低标定误差；

2) 影响相对方位角和相对距离的主要因素是经纬度误差和接收机x、y轴安装位置，但前者影响均稍大于后者；影响高度差的主要因素是高程和接收机z轴安装位置，两者影响相同。