半潜维修船配布的多层次规划模型

辛剑英, 谢新连, 何 平, 刘 毅

(大连海事大学 物流研究院， 辽宁 大连 116026)

半潜维修船是一种集海上维修保障、重大件运输和救助打捞等多功能于一体的新型高技术船舶。[1]按照我国海军由近海防御向近海防御和远海护卫型结合转变的战略目标：半潜维修船可实现舰艇维修从岸基转向海外机动保障，从而提高舰艇的综合保障能力；半潜维修船在没有军事任务的时期，可为我国海域内的商船或海上钻井平台等其他设备提供维修保障服务。鉴于半潜维修船对我国国防、经济等方面的战略支持地位[2]，有必要对其配布规划问题作进一步的研究。

半潜维修船的配布规划问题主要是为其选定停靠港或母港。半潜维修船在平时可从事重大件货物的运输或者商船的海上维修、救助等作业，在没有作业任务时一般停靠于母港待命。一旦接受到军事任务，负责特定海域的军舰维修保障任务的半潜维修船从母港出发，航行至军舰受损海域，提供维修保障服务。

由于半潜维修船是一种定位于军民两用的舰艇维修保障船舶，其停靠港的选址问题与应急设施选址问题类似，而这类问题具有特殊性，其作业应体现公平性、及时性和抗失效性等。对于这类问题，学者们已经提出了一些选址模型。BERMAN等[3]在最大覆盖模型的基础上提出将原有的0～1覆盖度扩展到多元覆盖，形成广义最大覆盖选址模型。朱建明[4]设定在设施失效情境下额外增加的应急时间，建立摧毁情形下的应急设施选址模型。葛春景等[5]建立阶梯型覆盖水平的多重覆盖模型。陆梦等[6]建立应急时间满意度的最大覆盖模型和集覆盖模型，解决海上溢油应急选址问题。基于以上研究，本文提出半潜维修船配布的多层次规划模型，该模型对舰船维修提供多层次覆盖，并且提出方法对每一层次覆盖质量进行评价。

1 半潜维修船配布的多层次规划模型

1.1 模型的描述

经典的选址模型主要包括：覆盖模型、p中值模型、p中心模型等3类，其中:覆盖模型又包括集合覆盖模型和最大覆盖模型等选址模型[7]，需求点和服务设施之间是单源性的，即1个需求点只由1个设施提供服务。文献[8]应用改进的p中值选址模型，提出一种半潜维修船停靠港的选址方案，然而,对于每个需求海域仅分配1艘半潜维修船，这样一旦负责某需求海域的半潜维修船出现正在执行任务或“失效”等突发状况，在实际操作中将出现责任划分不清的现象，该需求海域获得服务的时间将会大大延长，甚至需求海域可能无法得到服务[9]；另外，在考虑多重覆盖的前提下，对于需求海域是否被设施覆盖的标准则多是刚性的，即服务设施在一定时间或者距离内，则认为该需求海域被服务设施所完全覆盖，否者不被覆盖。这样的判断标准无法满足在半潜维修船停靠港的选址规划问题中的切实需要，在实际应用中，对于某特定的需求海域，所有设立的停靠港都是其“潜在”的服务供给点，其差别仅在于他们提供服务的质量不同，而不会出现超过一定的“边界”不提供服务这种现象；舰船维修具有受损频率小、一旦受损造成风险大的特点，故半潜维修船的配布计划应当在可接受的时间内使得半潜维修船能够覆盖更大的需求海域。综合以上考虑，本文基于最大覆盖模型，建立一种对于特定需求海域，给予多层次覆盖的规划模型，并且对每一个层次的维修保障质量进行评估，使半潜维修船的总维修保障质量达到最好。

半潜维修船配布的多层次规划模型是指对于特定的舰船维修需求海域，提供多种层次的半潜维修船服务，即多艘配布于不同停靠港的半潜维修船服务于同一需求海域，该需求海域同时被这些半潜维修船所覆盖，但是要按照距离将其划分为若干个服务层次(见图1)。并且，通过设定一定的临界距离或时间，对每一个层次的维修保障质量水平进行评价，在一定的距离范围内设定相同的质量水平，配布在不同港口的半潜维修船对于同一舰船维修海域的服务质量水平与距离成负相关关系；对超过一定距离范围的舰船维修海域，设定半潜维修船对其服务质量水平为0，认为该半潜维修船没有覆盖该海域。

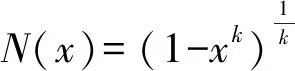
(1)

半潜维修船维修保障质量评价函数图像见图2。参数k=1/4、1/2、1、2、4时的维修保障质量评价值函数的图像，可根据实际需要选取适当的参数。

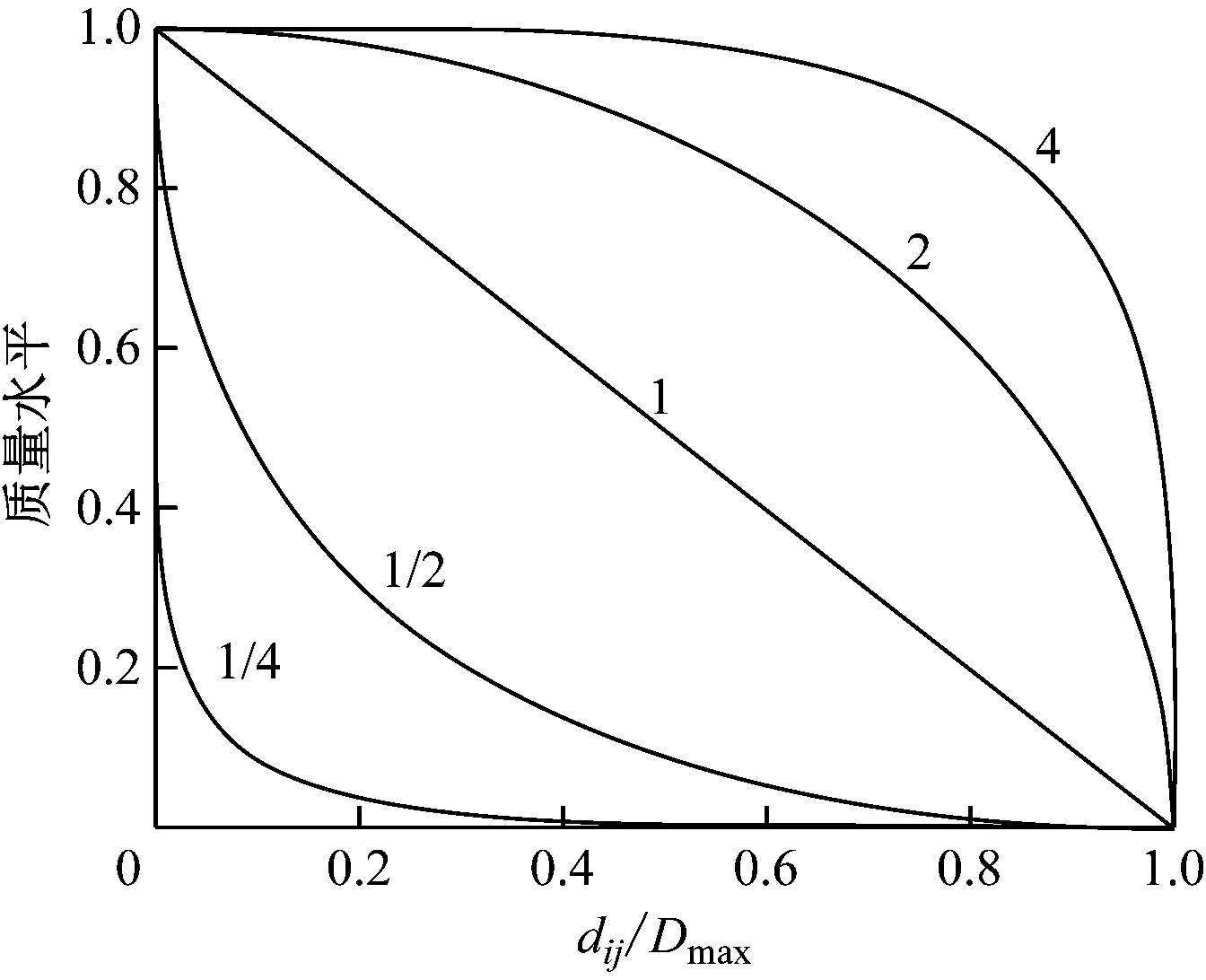
图2 半潜维修船维修保障质量评价函数图像

为便于对质量水平进行描述，规定函数值Q(dij)与覆盖级别的关系见表1。

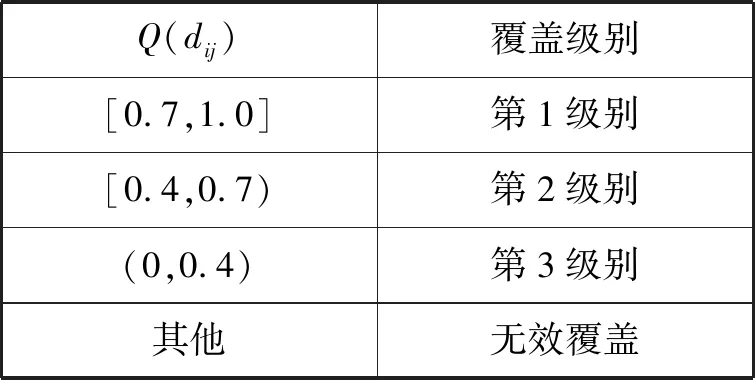
表1 Q(dij)与覆盖级别的关系

设I为舰船维修需求海域的集合

I={1,2,3,…,i}

(2)

J半潜维修船的备选停靠港集合

J={1,2,3,…,j}

(3)

p为设定选择半潜维修船停靠港的数量；wi为舰船维修需求海域i的需求权重。为解决问题之便，结合实际，对该模型提出以下假设说明：

1) 考虑到半潜维修船的造价及日常维护费用比较昂贵，对于规划的每个停靠港，只配布一艘半潜维修船。

2) 半潜维修船的维修保障能力无限制，即半潜维修船具有足够的维修能力，对受损舰船提供服务，将其完全修复，而不考虑其他因素。

3) 每个受损舰船维修需求海域均作离散点化处理，取其几何中心作为需求替代点，若某海域需取1个以上需求点，则对该海域先进行均匀分割，再对分割后每个区域取几何中心。

1.2 模型建立

半潜维修船配布的多层次规划模型为

(4)

(5)

(6)

xij≤yj,∀i∈I,∀j∈J

(7)

yj,xij∈{0,1},∀i∈I,∀j∈J

(8)

式(4)为目标函数，表示在多层次的半潜维修船规划模型下，使受损舰船得到的维修保障质量的总评价值最大化；式(5)表示共选取p个港口作为半潜维修船的停靠港；式(6)表示对于特定的维修保障需求海域最多存在r艘半潜维修船为其提供服务，r值根据决策者欲配置的层次规划数确定，如决策者欲进行半潜维修船的双层次规划，则r取2；式(7)表示只有被选择作为停靠港的港口才能为受损舰船提供服务；式(8)是决策变量的0～1约束条件,yj=1表示j港被选为停靠港，yj=0则否；xij=1表示j港的半潜维修船为海域i的舰船提供服务，xij=0则否。

海域的需求权数wi衡量各区域对半潜维修船维修保障服务的需求程度。显然，权重的大小体现于海上事故风险的强弱，海域i发生事故风险概率越大，事故的影响程度越大，则其对于半潜维修船的维修保障服务的需求便越高，即海域的事故风险越大，则需求权数越大，故此处通过评估海上事故风险以确定需求权数。本文采用海上事故风险评估模型[10]，海上事故风险值Ri的表达式为

Ri=f(Pi,Ei)

(9)

式(9)中：Pi为海域i发生风险的概率；Ei为海域i风险发生的影响程度。

Ei=f(Ci,Ai)

(10)

Ci=Di×Si×Ti

(11)

式(10)和式(11)中:Ci为海域i发生事故可能造成的损坏程度;Ai为资源的重要性;可能损坏度由事故危险系数Di、船舶尺度系数Si以及船舶类型系数Ti共同确定，最后得到海域风险评估模型

Ri=Pi×Di×Si×Ti×Ai

(12)

海域风险Ri可通过查询各海域的历史事故统计数据进行计算评估，则海域i的需求权重wi的表达式为

(13)

1.3 模型求解

最大覆盖模型已经被证明属于NP难问题，本文提出的模型是最大覆盖模型的变形，因此也属于该类问题。为求解该类问题，专家们提出许多解法，其中以启发式算法为主，如遗传算法、模拟退火算法、蚁群算法等。本文采用免疫优化算法进行求解。免疫优化算法与遗传算法有许多相似之处，而免疫优化算法除了仍然使用“适应度”来评价解的优劣，即“适应度”越高，被选择的概率越大,还增加了“抗体浓度”，即解之间的相似程度。相似程度越高，被选择的概率会越低。两者结合，共同构成解的评价机制。算法具体步骤如下：

1) 初始抗体群。使用实值编码方案，对所有备选港由1到m分别赋值。随机产生N个抗体，每个抗体是长度为p，随机生成 [1，m]的数组，并从记忆库中选取L个个体构成初始种群(见图3)。例如，第1条抗体代表选取港口j=1,3,5,6,8,9作为停靠港。

图3 编码说明

2) 抗体的评价。个体的评价值由个体的期望繁殖率P来确定。

(14)

式(14)中:参数α为常数，可根据使用者需求选取，若α取1，则免疫优化算法与遗传算法相同，选取合适的α值，可实现既鼓励适应度高的个体，又能确保个体多样性的目的；Av=z，评价适应度的质量，适应度值由式(2)确定，对于每一个需求点i，计算抗体中港口j的半潜维修船对其的服务质量评价值Q(dij)，并进行降序排序，选取前r个Q(dij)。遍历所有需求点，得到“适应度”值，即抗体浓度。

(15)

图4 “亲和力”示意

3) 形成父代群体。按期望繁殖率P将初始群体降序排列，提取前n个作为父代群体，同时提取前L个更新记忆库。

4) 判断是否满足结束条件，若否则进行下一步。

5) 解空间的改良。取3)中的父代群体进行选择，交叉，变异操作，作为新群体。其中，交叉操作可能会出现现象见图5，这时采用“基因修复”的方法进行处理。然后,提取记忆库中的个体，共同构成新群体。返回2)。

2 案例分析

2.1 备选停靠港及海域需求权重的确定

半潜维修船备选停靠港的选择，应该结合我国

图5 交叉运算说明

沿海大型港口的数量、分布及其功能定位等因素综合考虑。此外，值得注意的是，必须紧密联系我国当前的救捞系统框架综合分析，确定半潜维修船的备选停靠港。交通运输部救捞局资料显示:我国救捞总布局为自北方沿海的秦皇岛、大连、天津、烟台等地直至南部的湛江、海口、三亚、西沙，总计配置24个基地，提供海上救助力量。结合对各港口的分析，本文选择大连、天津、烟台、连云港、上海、宁波、温州、福州、厦门、深圳、海口、西沙等12个港口作为备选停靠港(j=1,2,3,…,12)。

配布半潜维修船的主要目的是对我国海域内的军舰或商船提供维修保障服务，以起到保障国家安全和支持经济建设的作用，故本文选择我国的渤海、黄海、东海、南海等四大海域作为研究对象，将这4大海域作离散点化处理，并且根据海域面积的比重确定各海域需求点的数量，分别为渤海1个、黄海2个、东海3个、南海4个需求点(i=1,2,3,…,10)。

最后根据4大海域发生海上风险事故的历史数据，确定舰船维修需求海域的需求权重，半潜维修船备选停靠港与需求海域距离dij和权重系数wi见表2。

2.2 模型的求解

式(1)中，对于参数k，有:当k=1时，该函数为线性函数，距离dij对质量水平的影响随线性递减；当k>1时，该函数为凸函数，起初质量水平的变化随距离dij增长变化较为缓慢，经过函数拐点后，质量水平随距离dij增长急剧下降；当01所述情况相反。应用时应根据具体情况选取，本文选取k=2。

半潜维修船的设计航速在14 kn以上，以48 h内是否可以到达需求海域为临界时间，确定Dmax=680 n mile。利用设计的免疫优化算法对该模型进行求解，得到不同的配布方案中，半潜维修船数量p与受损舰船的维修保障质量评价值z的关系见表3。

表2 半潜维修船备选停靠港与需求海域距离和权重系数 n mile

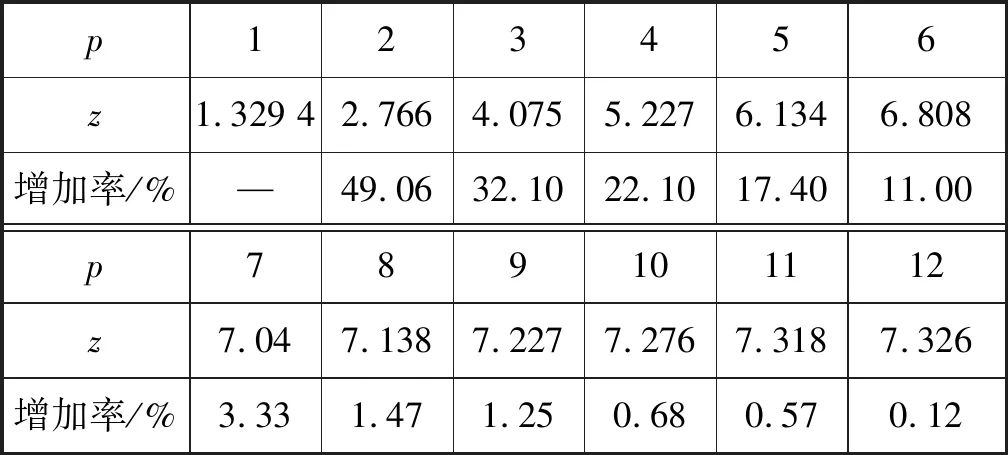
表3 p与z的关系

计算结果显示:维修保障质量z随配布的半潜维修船数量p增加而上升，当数量由p=6增加到p=7时，维修保障质量z变化速率较小，这表示维修保障质量没有因为多配布一艘半潜维修船而明显提升。实际上，半潜维修船的造价和日常维护费用都比较昂贵，当数量达到p=6，配布更多的半潜维修船是不经济的，同时也是对运力的浪费。基于配置适当数量的半潜维修船，同时要保证舰船维修的服务质量的考虑，不配置6艘以上半潜维修船。将半潜维修船的数量p=5和p=6时的规划方案对比研究(见表4和表5)。

按照设定的维修保障质量水平描述方法，上面的两个表格显示:当p=5时，存在4个海域需求点仅规划2个层次的维修保障服务，并且对海域i=1，即渤海海域，没有提供第1级别的维修保障服务；而当p=6时，除需求海域i=9以外，其他所有海域都得到3个层次的维修保障服务，每一个需求海域都能得到第1级别的服务，并且不存在第3级别的服务，能为案例中受损舰船维修保障需求海域提供良好的服务，p=6时，各需求海域的维修保障质量评价值见表6。

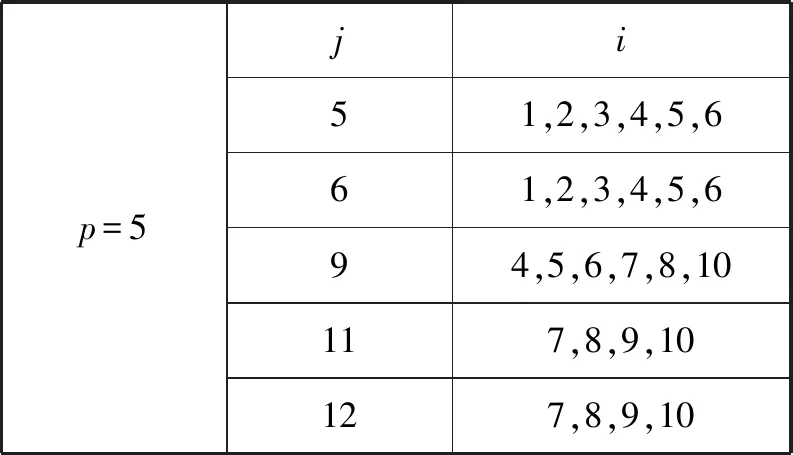
表4 半潜维修船配布情况

表5 半潜维修船配布情况

半潜维修船的配布规划应当体现“公平性”，即各个需求海域应最大程度地享有同样水平的服务，故基于p=6的半潜维修船配布计划，建议在连云港、上海、宁波、厦门、海口和西沙各配布1艘半潜维修船。

表6 维修保障质量评价值(p=6)

3 结束语

传统的选址模型，在半潜维修船停靠港的规划问题上存在很大局限性，无法很好地保证对需求海域的维修保障质量，故在最大覆盖模型基础上，建立半潜维修船的多层次规划模型。

1) 对传统的“覆盖”概念进行拓展，应用模糊规划的相关理论，引入“覆盖水平”的概念，弥补了传统模型中0～1覆盖的缺陷。

2) 对需求海域的服务单源性进行改善，建立多种层次的服务体系，对半潜维修船执行任务或其他原因无法提供方案，同时也避免实际中的责任划分不清的情况。

3) 应用免疫优化算法对该模型进行求解，该算法具有收敛快和解的精度高等优势。

4) 结合我国救捞布局、海上风险分布及收集数据，求解得到我国半潜维修船的配布方案。