A Novel Multi-Hop Algorithm for Wireless Network with Unevenly Distributed Nodes
Yu Liu, Zhong Yang, Xiaoyong Yan, Guangchi Liu and Bo Hu
Abstract: Node location estimation is not only the promise of the wireless network for target recognition, monitoring, tracking and many other applications, but also one of the hot topics in wireless network research. In this paper, the localization algorithm for wireless network with unevenly distributed nodes is discussed, and a novel multi-hop localization algorithm based on Elastic Net is proposed. The proposed approach is formulated as a regression problem, which is solved by Elastic Net. Unlike other previous localization approaches, the proposed approach overcomes the shortcomings of traditional approaches assume that nodes are distributed in regular areas without holes or obstacles, therefore has a strong adaptability to the complex deployment environment.The proposed approach consists of three steps: the data collection step, mapping model building step, and location estimation step. In the data collection step, training information among anchor nodes of the given network is collected. In mapping model building step, the mapping model among the hop-counts and the Euclidean distances between anchor nodes is constructed using Elastic Net. In location estimation step, each normal node finds its exact location in a distributed manner. Realistic scenario experiments and simulation experiments do exhibit the excellent and robust location estimation performance.
Keywords: Multi-hop localization, Elastic Net, regularization, sparse.
1 Introduction
As a new media, wireless network can realize communication between people and object,and it has been broadly used. However, the location of people or object in the network is the basic information for communication. Current wireless localization technologies include GPS-based [Wang, Lu, Wang et al. (2017)], infrared-based [Park, Cho, Kim et al.(2014)], Bluetooth-based [Castillo-Cara, Lovó n-Melgarejo, Bravo-Rocca et al. (2017)],RFID-based [Zhou and Shi (2009)], WIFI-based and UWB-based [Mazhar, Khan and Sä llberg (2017)], etc. Among them, GPS-based application is the most mature localization application with broadest application, but when there are obstacles, it is very difficult to satisfy the application requirement on the aspect of localization precision; the infrared ray has short propagation distance, which also tends to be interfered with by fluorescent lamp or indoor lighting, and there is certain limitation during localization;both the Bluetooth technology and RFID technology apply to indoor localization, but the Bluetooth technology has poor stability in complicated environment and system, while the RFID technology has short transmission distance, and it does not have the communication capacity; during the WIFI localization, the transmitter and receiver can only cover an area within 90 m, but it tends to be interfered with by other signals, and its locator involves high energy consumption; the UWB localization method can provide centimeter-level localization precision, but it is difficult to capture the UWB signal, and it also tends to cause significant interference with other signals. With the introduction of new wireless networks such as IoT (Internet of Things) and Mesh, wireless nodes can be randomly deployed in various types of monitoring environment, and the location information can be exchanged through the methods of multi-hop and self-organization.
The node localization method based on multi-hop and self-organization is called the“multi-hop localization” method. The multi-hop localization method can be roughly divided into two groups of range-based and range-free methods according to whether it requires range finding during the localization process [Yang, Wu and Liu (2014)]. The localization precision of range-based method depends on the measuring equipment, so it requires high equipment cost, and it is restricted to large-scale application. The range-free localization method is a localization technique of cost-effective and less limited for a wider range of applications, and it does not require direct measuring between nodes during the localization process, so this method has attracted more attention. The rangefree technique generally employs hops to describe the Euclidean distance be-tween nodes,and the locations of unknown nodes are estimated with the assistance of trilateration. By replacing the multi-hop localization of directly measuring with hops, it tends to be affected by node distribution. Under high density and even distribution of nodes, the range-free method can provide excellent localization performance; however, when the nodes have sparse and uneven distribution, it has very poor localization performance.Unfortunately, in an real environment, due to various reasons such as random distribution of nodes, obstacles and communication failure of nodes, after the network topology is determined, the whole network would present uneven distribution under the influence of its own or external factors. Due to uneven distribution of nodes in the network, it would generate severe deviation by using hops to describe the Euclidean distance with rangefree localization method [Liu, Zhang and Bu (2016)].
Take Fig. 1 as an example, we use dotted lineto represent the Euclidean distance between nodesin the network, and use arrowed straight lineindicate the approximate length of the shortest path between nodesandWhen the nodes are distributed evenly and densely in the network, we can see that, however, when nodes are unevenly distributed or obstacles affect the signal transmission, the nodes are distributed unevenly, which will result in
Therefore, we can intuitively understand that if the nodes in the network are evenly distributed, the Euclidean distance between pairs of nodes is proportional to the hop count; conversely, the proportional relationship between the Euclidean distance and the hop count no longer holds.

Figure 1: Nodes uneven distribution network
According to the above analysis, it is not difficult to see that when there are phenomena such as lack of distribution and uneven distribution of nodes, the hops between nodes will change, which will cause severe error during the estimation process of the shortest path.This kind of estimation error of the shortest path is directly related to the orientation of the shortest path, and the shortest path which does not pass through the area with uneven node distribution will not be affected. The distance estimation of shortest path between nodes is the basis of multi-hop localization problem, and only when the distance estimation error of shortest path between nodes is small can the localization of unknown node be conducted in a relatively accurate way; when the distance estimation error of shortest path between nodes is big, the localization precision of unknown node will be severely affected. In order to increase the adaptive capacity of range-free multi-hop localization method for various types of environment, we propose a range-free localization algorithm with high localization precision, which can adapt to various types of anisotropic network environment, i.e. Multi-hop Localization through Elastic Net(ML-EN). The Elastic Net method [Zou and Hastie (2015)] can be used to effectively handle strongly correlated variables, effectively choose variables and estimate related parameters, so the ML-EN method can provide higher localization precision and adapt to different network environment.
2 Relation work
DV-Hop is the best-known range-free multi-hop localization algorithm, which was proposed by Niculescu et al.[Niculescu and Nath (2003)] from Rutgers University, and this algorithm has been broadly discussed and quoted. The DV-Hop algorithm is built on some simple idea and easy to realize. In this algorithm, the distance from the unknown nodes to the anchor nodes are represented by the product of the per hop distance and the hops, and finally, the trilateration is used to estimate location of unknown nodes. The distance estimation method of DV-Hop algorithm has strict requirements on the distribution of nodes, which results in poor adaptability. According to the problem of uneven distribution of nodes, Shang et al. [Shang, Shi and Ahmed (2004)] proposed a method to use only four nearest anchor nodes from the unknown nodes to locate the unknown node (for convenience of discussion, we call this algorithm the “Nearest-4 algorithm”). The Nearest-4 algorithm believes that the fewer hops between nodes, the less affected by the uneven distribution of nodes. However, some unknown nodes may have few anchor nodes at close range and have to choose anchor nodes at a longer distance. In addition, the mechanism of selecting the most nearest four anchor nodes as reference nodes will also exclude some anchor nodes that are far away but have better distance estimation, thereby reducing the localization accuracy of unknown nodes.Shahzad et al.[Shahzad, Sheltami and Shakshuki (2017)] proposed the DV-maxHop method based on the Multi-objective Optimization method. The algorithm found that the value of MaxHop in the range of 5 to 15, gives satisfactory results. Recently, Zhao et al.[Zhao, Su and Shao (2018)] proposed the LWLR-DV-hop method based on the Nearest-4 algorithm. In this algorithm, three anchor nodes nearest to the unknown node are chosen as the reference nodes, and the local weighted least square method is used to further weaken the deviation between hops and Euclidean distance conversion.
In recent years, various improved DV-hop algorithms have been continuously proposed,but these improved methods still use the average hop distance from the unknown node to the anchor node to estimate the distance, and this kind of distance estimation method has the defects of poor model interpretability and poor adaptation to the nodes distribution.According to the defects of the DV-hop algorithm and its improved methods, the Hou research team at UIUC proposed the PDM algorithm [Lim and Hou (2009)]. The PDM algorithm directly adopts the skeleton between reference nodes to build the mapping model between hops and Euclidean distance, and the least square method is used to obtain the optimal linear conversion between hops and Euclidean distance. In essence,PDM is used to estimate the distance between nodes based on the hop-by-hop transmission characteristic of wireless network data, so there tends to be correlation between the hop matrix vectors during the estimation process. Take Fig. 2 as an example assumeis the source node andis the destination node, and because it needs to pass through nodesfrom, there is also close correlation between the hop matrix vectors between nodes. When there is correlation between the hop matrix vectors, it needs to be penalized during the estimation process (i.e.regularization). Based on this problem, in the PDM algorithm, the TSVD regularization method [Hansen (1987)] is adopted during construction of the mapping model between hops and Euclidean distance.
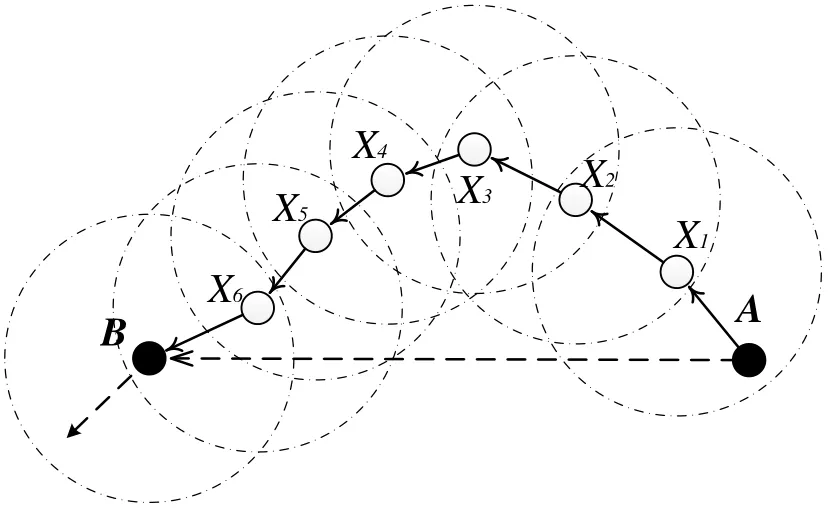
Figure 2: Node communication model in multi-hop networks
Compared with many previous DV-hop and its improved algorithm, the PDM method can more accurately capture the relation between hops and Euclidean distance, and effectively dig the node distribution and correlation information hidden behind data, so it can effectively improve the multi-hop localization performance. However, the PDM method has ignored the magnitude order conversion problem between hops and Euclidean distance, so it tends to cause fluctuation in localization performance of algorithm under different node densities and node communication radiuses. In addition,the regularization method adopted by the PDM method is essentially a method with empirical risk minimization, so the final localization performance of the PDM depends on the distribution of anchor nodes in the network. When there are a small number of anchor nodes, this method can only guarantee the localization precision of nodes near the anchor nodes. Inspired by the PDM method, Lee et al. [Lee, Chung and Kim (2013)]proposed two range-free multi-hop localization algorithms based on support vector regression, which are LSVR and MSVR respectively. By introducing the kernel function,these two algorithms adopt nonlinear mapping method to transform the localization problem to kernel regression problem. The support vector regression is a method with minimum structural risk, so the LSVR and MSVR methods are still able to provide great localization performance with a small amount of reference nodes. However, according to the bias-variance tradeoff theory of statistics and machine learning, it tends to cause the over-fitting problem when there a large number of model parameters. During actual application, the LSVR and MSVR algorithms are significantly affected by the over-fitting problem, and it might have poorer localization performance than some early PDM methods under certain scenarios. Take Fig. 3 as an example, Fig. 3(a) shows a classic network with uneven node distribution, there are 300 nodes in the network, and 36 of them are anchor nodes. Fig. 3(b) shows the results obtained with the LSVR localization method, where the circle represents the estimated location of the unknown node, the straight line connects the real coordinates of the unknown node and its estimated coordinates, and the longer the straight line, the greater the localization error. Obviously,LSVR is affected by the over-fitting problem, and the unknown node’s estimated location tends to be a curve.
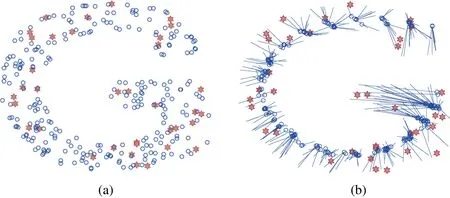
Figure 3: (a) Node distribution, (b) localization result
Later, in 2016, Yan et al. [Yan, Song and Liu et al. (2015)] used the ridge regression (RR)to replace the multi-parameter SVR method and proposed the LRR localization algorithm,and the localization precision of algorithm has been significantly improved. The model built with RR is stable, it improves the prediction precision by reducing the estimation variance, but it has increased the estimation bias. In other words, the RR is a continuous method, which has reduced the regression coefficient without simply abandoning any variable. Because ridge regression fails to reduce any regression coefficient to 0, there are too many variables in the built model, and the model has poor interpretability. Again,take Fig. 4 as an example, assumeis the source node andare the destination nodes. According to the neighborhood in Fig. 4, we can see thatonly have common path on the two nodes of. Therefore,are only correlated at, and it is obviously unreasonable to impose penalty on the two paths ofwith no correlation.
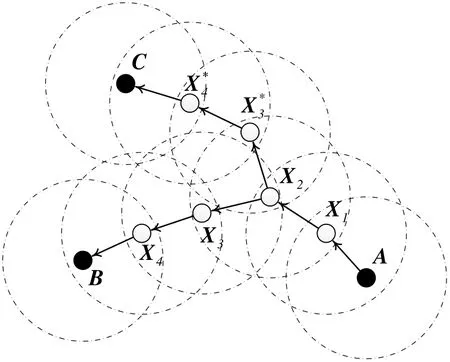
Figure 4: Multiple communication path model in multi-hop networks
In 1996, Tibshirani [Tibshirani (1996)] proposed a landmark new variable selection method-LASSO. Different from the idea of traditional variable selection method, this method uses the absolute value function of model coefficient as penalty to compress the regression coefficient of model, so that some coefficients with smaller absolute value won’t be directly compressed to 0, which can not only realize selection of significant variable, but also provide corresponding coefficient estimate. Although the LASSO method has some great properties, and it has been broadly used, some of its defects are also reflected in actual application. For example, the LASSO method does not have group's effect, which results in poor accuracy and effects. In addition, the LASSO method does not distinguish between various decomposition coefficients, it provides compression with the same degree, and this will cause over compression of some coefficients, which will further affect the estimation accuracy. In order to address these problems, in 2005, Zou et al. [Zou and Hastie (2015)] proposed the Elastic Net method.This method has combined the merits of both RR and LASSO, which has not only kept the stability of RR, but also possessed the characteristic of variable selection, and as a result, the estimation accuracy can be effectively improved.
3 Network model and localization problem description

4 Node location estimation
The basic idea of multi-hop localization based on the Elastic Net is to transform localization to regression prediction problem by building the mapping relation between hops and Euclidean distance. The ML-EN algorithm consists of three steps (as shown in Fig. 5): First of all, measure the hops and Euclidean distance information between anchor nodes; then, build the mapping model between hops and Euclidean distance through EN;finally, estimate the coordinate of unknown node by the multilateration method.
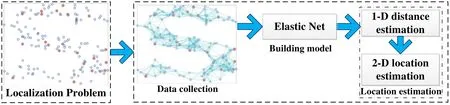
Figure 5: The framework of proposed algorithm
The details of above three steps are discussed in the following subsections.
4.1 Measurement step
First of all, after the program starts, any anchor nodewill broadcast a HELLO packet to other nodes in the network. After the program has run for a while, the anchor node can obtain the shortest hops from it to other nodes. Then, the anchor nodewill send an INFO packet to other anchor nodes in the network, and the packet contains the information of its own locationand the shortest hopsto other nodes. In this way,any anchor node in the network can build a global shortest hop matrixbetween anchor nodes and a distance matrixbetween anchor nodes.
4.2 Model building step
Through data collection during the measurement stage, any anchor nodecan collecthops-Euclidean distance data pairswhich can connect the anchor nodewith the rest anchor nodes in the network. Assume the constraint condition for localization is a mapping function


In order to obtain optimal distance estimation model, Elastic Net can be used for estimation, and the objective function of EN is:

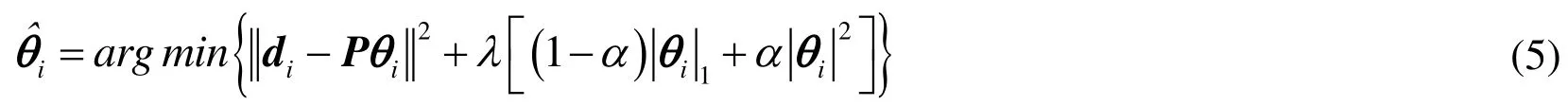
In order to obtain the optimal estimation for Formula 5, i.e.the optimal hops-Euclidean distance conversion model, we can use data pairand the penalty coefficientsandto build a new training dataset

The optimal conversion modelbetween hops and Euclidean distance from anchor nodeto other nodes in the area can be expressed as:

At this moment, the Least Angel Regression [Efron, Hastie, Johnstone et al. (2004)] and AIC criterion [Akaike (2011)] can be used to obtain the optimal conversion modelAccording to the Elastic Net, in the optimal solutionobtained from Formula (7), some penalty coefficients for nodes with weak correlation will be compressed to 0, so that the hops-Euclidean distance conversion model will have sparsity.
4.3 Location estimation step
Through model building step, any unknown nodehops-Euclidean distance conversion models and shortest hops vectorsfrom the anchor nodes. Let

be the estimated distance vector representing the estimated distance between the unknown nodeanchor nodes. The estimated distance vectorcan be determined by

After the estimates of the distancesto the anchor nodes are evaluated, multilateration is performed to localize the location of the node
5 Performance analysis
In this section, through experiments in various environments, the performance of multihop localization algorithm based on the EN algorithm will be analyzed and evaluated.First of all, a group of experiments were conducted in the actual environment (as shown in Fig. 6). In the actual environment, the experiments were conducted in an indoor corridor, and its scope was around. We deployed 20 wireless nodes in the corridor, and the node chip is CC2530 produced by TI Company.
Because this paper is dedicated to addressing the influence of uneven node distribution on the localization performance, we will not focus on such factors as the node communication cost, node lifecycle and information delivery method. In the experiment,the influence of the indices of node distribution, proportion of anchor nodes and node density on the localization precision was mainly investigated.
Sometimes, it is difficult to set these parameters. Therefore, in this section, we will still evaluate the performance of localization algorithm through software simulation.

Figure 6: (a) Wireless node; (b) Node distribution scenario; (c) Network topology with 20 nodes
We use the root mean square (RMS) as the criterion for localization precision, and RMS can be expressed as:

We also compare our method with seven previous methods: (1) the classic DV-hop algorithm proposed in Niculescu et al. [Niculescu and Nath (2003)]; (2) Nearest-4 proposed in Shang et al. [Shang, Shi and Ahmed (2004)]; (3) DV-Maxhop proposed in Shahzad et al. [Shahzad, Sheltami and Shakshuki (2017)]; (4) LWLR-DV-hop proposed in Zhao et al. [Zhao, Su and Shao (2018)]; (5) PDM proposed in Lim et al. [Lim and Hou(2009)]; (6) LSVR proposed in Lee et al. [Lee, Chung and Kim (2013)]; and (7) LRR proposed in Yan et al. [Yan, Song, Liu et al. (2015)].
5.1 Localization experiment in real scene
During the multi-hop localization, the hops between two nodes can be determined by setting the threshold value of signal attenuation. Therefore, it requires obtaining the relation between signal attenuation value RSSI and the distance. In order to obtain the relation between RSSI and the distance, for the scenario as shown in Fig. 6, we repeatedly collected communication among 20 nodes for 120 times. Considering that in the actual environment, the signal reflection, scattering or shielding will generate interference with the signal value collected by receiving node, we adopt the Log-normal Shadowing model [Yang, Wu and Liu (2014)] to depict how the signal intensity will change with the change of distance.

After collecting 120 times of data, we adopt the method in Literature [Yan and Qian(2013)] to clean the signal data, and after eliminating outlier signal values caused by the environmental factors, the mean value of signals collected in multiple times is used. In the environment as shown in Fig. 6, at a distance of 1 m, the mean value of RSSI obtained through multiple measurements is -31.55 dBm.
Up until now, we have obtained the signal and distance distribution diagram in the area of Fig. 6 (as shown in Fig. 7).
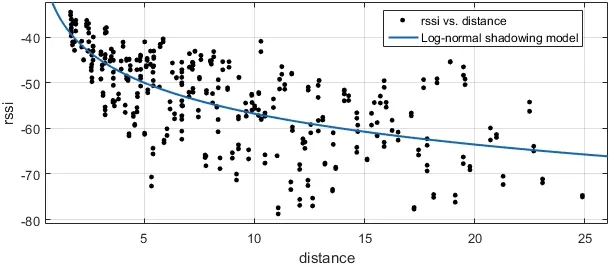
Figure 7: RSSI vs Distance plots for the 20 node deployment indoor
According to Formula 11, we can obtain the distance prediction formula,

In this group of experiments, the node communication radius is set at 4.5 m; nodes 4,6,10,12,13 and 15 in the network are chosen as the anchor nodes, and the rest 14 nodes are nodes to be localized. The Matlab software was used for computation of the ML-EN algorithm proposed in this paper and other 7 similar algorithms, and the final localization result can be obtained (as shown in Fig. 7). According to Fig. 8, we can see that the DVMaxhop algorithm has close estimation precision as the DV-hop algorithm. This is because of the restriction of deployment space, which has resulted in failure of hops selection in the DV-Maxhop algorithm, and the DV-Maxhop algorithm will degrade to the DV-hop algorithm. The Nearest-4 algorithm and LWLR-DV-hop algorithm are two algorithms with similar theoretical basis, but due to restriction of the number of selectable anchor nodes and the topologic quality of anchor nodes, their localization precisions are lower than that of the DV-hop method. Fig. 8(h) shows the ML-EN method proposed in this paper, it has high localization precision, and the RMS value is 4.5595. The average localization precision (RMS) of ML-EN method is 58.1%, 68.2%, 61.1%, 39.3%,4.2%and 6.4% higher than the localization precisions of Nearest-4, DV-Maxhop, LWLR-DV-hop, PDM, LSVR and LRR methods respectively.
For localization in the actual environment, we also employ the Cumulative Distribution Function (CDF) to analyze the accumulative distribution of errors of nodes to be localized. We can find when using ML-EN, the localization performance is effectively improved, e.g.more than 80% nodes are localized with RMS is less than 4 m in the realworld environment.
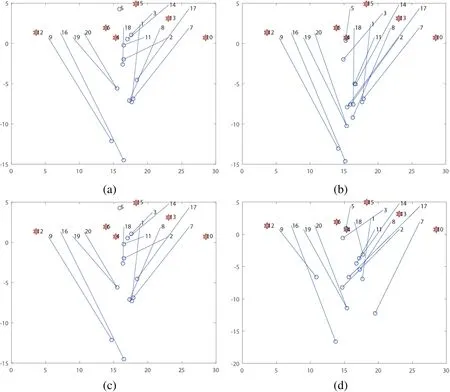
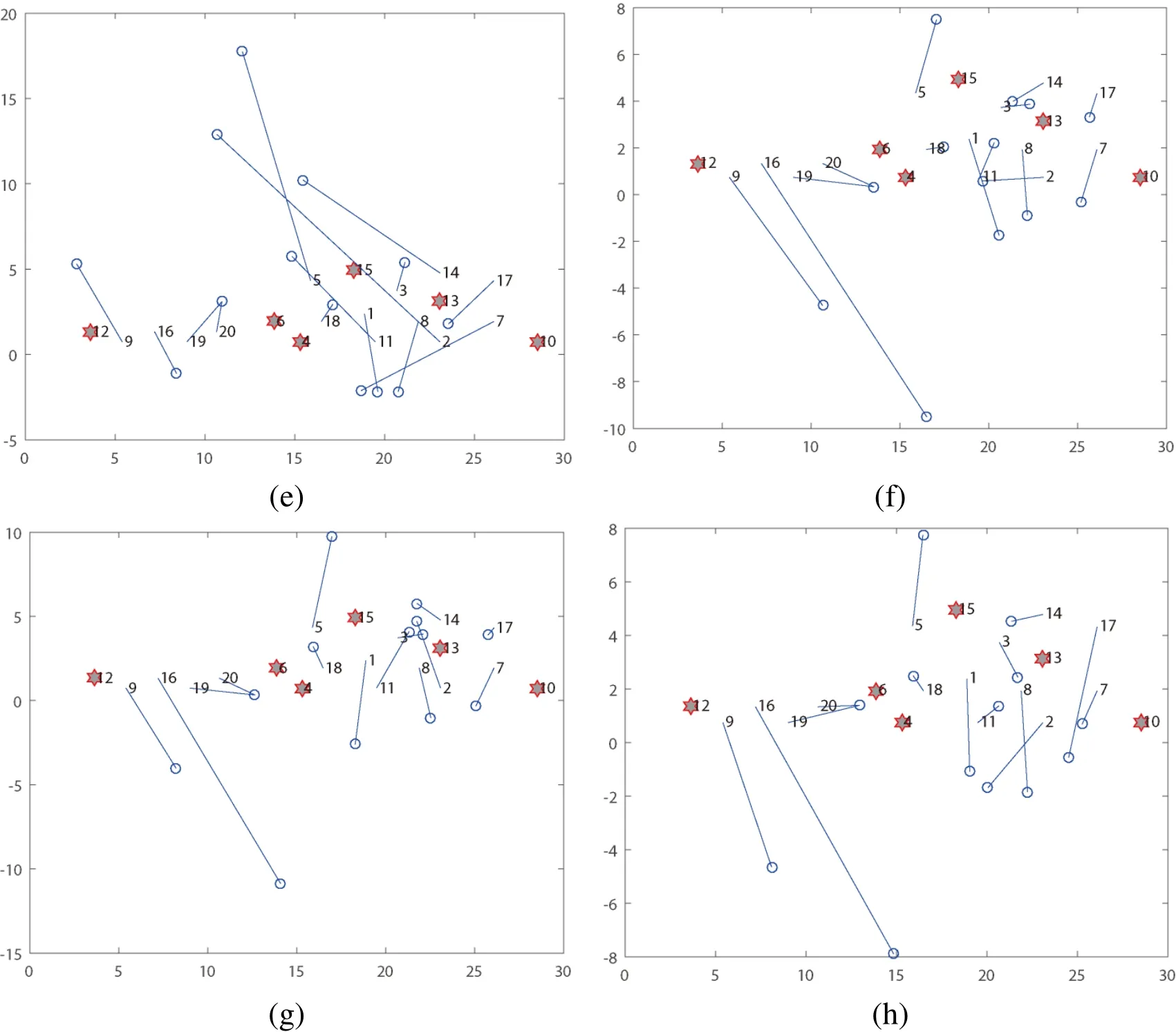
Figure 8: Results of location estimation in realistic scenarios. (a) DV-hop, RMS=9.9152;(b) Nearest-4, RMS=12.0545;(c) DV-Maxhop, RMS=9.9152; (d) LWLR-DV-hop,RMS=11.4967; (e) PDM, RMS=7.5795; (f) LSVR, RMS=5.0697; (g) LRR, RMS=5.0385(h) ML-EN, RMS=4.5595

Figure 9: The CDF of the estimation errors in realistic scenarios
5.2 Simulation experiment
In this section, the performance of localization algorithm based on Elastic Net will be analyzed and evaluated through simulation experiment. The experiment analyzes the distribution of nodes in the network, the proportion of anchor nodes, and the density of nodes. The specific parameters of the network are shown in Tab. 1.

Table 1: Network parameters
5.2.1 The uneven distribution of nodes
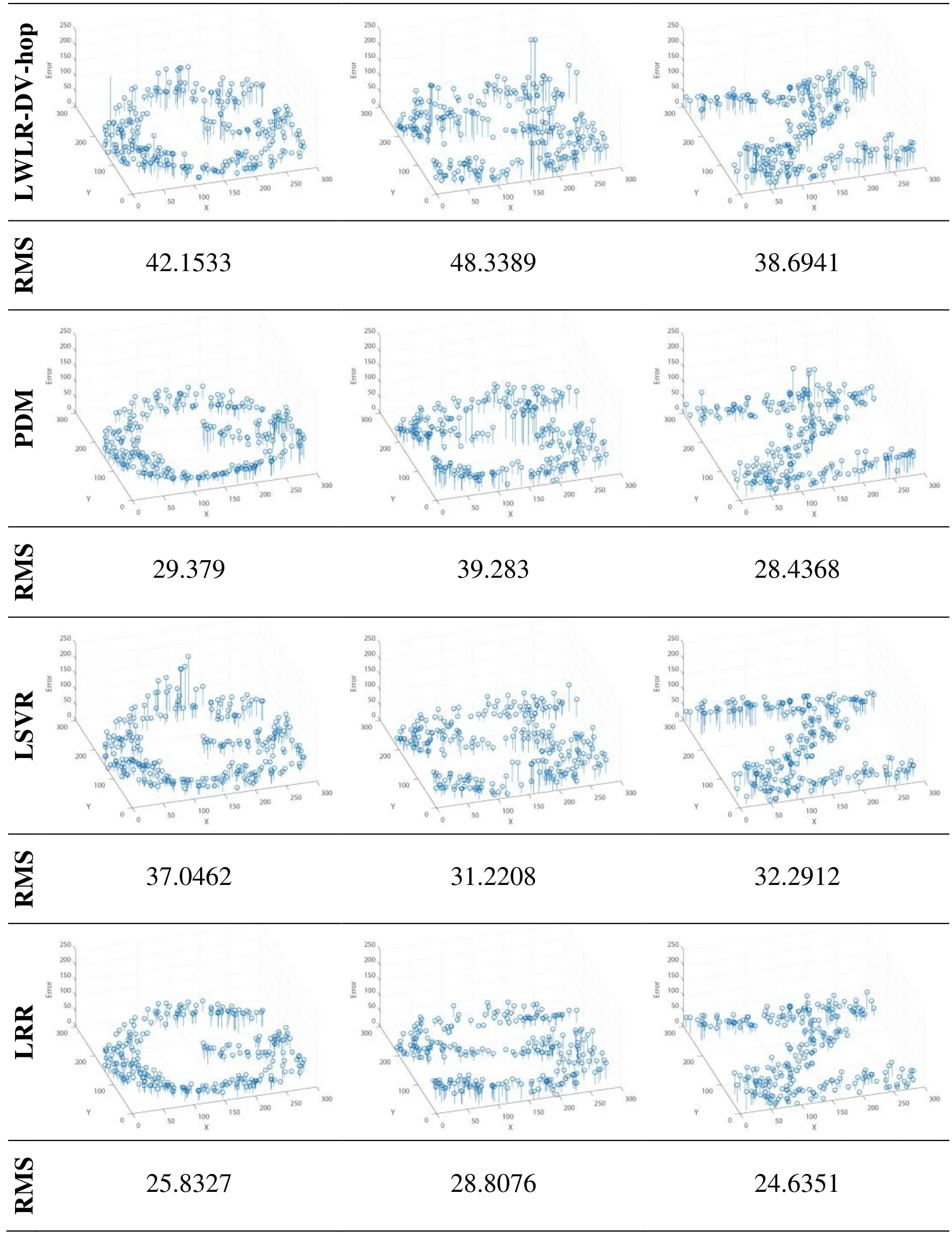
Experiments adopt the distribution of letter-shaped nodes to simulate the uneven distribution of nodes. Tab. 2 describes the node distribution and localization results of ML-EN and similar algorithms when the node communication radius is 40 and the anchor nodes account for 12% of total nodes. The first line in Tab. 2 shows the node distribution.The localization results are described with 3-D stem plot, the stem height represents the absolute error of estimation, and the higher the height is, the bigger the localization error.

Table 2: Localization results with different nodes distribution
?

?
According to the localization result in Tab. 2, we can see that in a network with uneven node distribution, because DV-hop and its improved methods use fixed hops-Euclidean distance conversion coefficient, it results in error during the conversion between hops and Euclidean distance; although the PDM method can solve the error generated during conversion from hops to physical distance, however, due to restriction by problems such as conversion of magnitude order and minimum empirical risk, the improvement of localization performance is very limited; the LSVR method is restricted by the overfitting problem, which causes its localization precision to be higher than that of the PDM method; although the LRR method has higher localization precision than previous methods, the improvement in precision is limited due to fixed ridge parameter, The MLEN method proposed in this paper has considered various factors constraining the localization precision, so it can provide higher localization precision.
5.2.2 Anchor node ratio
Another factor that affects the estimation accuracy of the nodes is the ratio of anchor nodes. In order to reduce the one-sidedness of the experimental results, we conducted 100 simulations for each node distribution network. Considering that the boxplot will not be affected by outliers, and it can describe the discrete distribution of data in a relatively stable way, in this group of experiments, we use boxplot to describe the localization results of multiple simulation experiments under different proportions of anchor nodes(8%~16%).
In Fig. 10, the experimental results show that the DV-hop method does not apply to the localization in anisotropic network. In the G-shape network and S-shape network, its RMS values are both higher than 100; in the Z-shape network, its RMS value is between 70 and 120, which also presents fluctuations with the increase of anchor nodes. The Nearest-4, DV-Maxhop, LRR methods and the ML-EN method proposed by us all have higher localization precision than the DV-hop method, and the precision presents gradual decline with the increase of anchor nodes. The ML-EN method proposed in this paper has the lowest RMS values in all three networks with uneven distributed nodes: in the G-shape network, the average estimation accuracy of ML-EN method is 83.85%, 67.33%,57.26%, 51.9%, 35.53%, 43.98% and 24.95% higher than that of the DV-hop, Nearest-4,DV-Maxhop, LWLR-DV-hop, PDM, LSVR and LRR methods respectively; in the S-shape network, the average estimation accuracy of ML-EN method is 83.26%, 65.51%,59.7%, 51.05%, 34.64%, 44.51 % and 22.12% higher than that of the LRR method; in the Z-shape network, the average estimation accuracy of ML-EN method is 77.86%, 62.42%,57%, 48.01%, 32.1%, 40.04% and 18.97% higher than that of the Nearest-4 and LRR methods respectively.
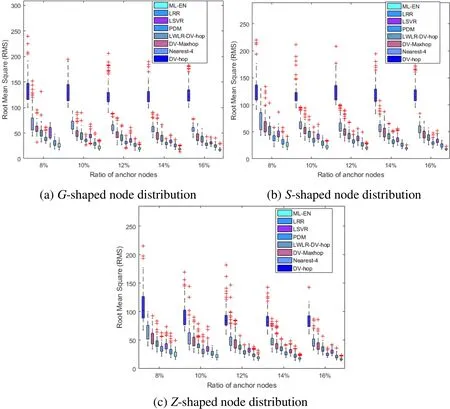
Figure 10: Simulation results of the different algorithms with different number of anchors
5.2.3 Node density
In this section, we also evaluate the effect of node density on positioning errors. The number of nodes’ average neighborsis usually used to represent the node density, whereis the size of the node deployment area,is the node communication radius, andis the number of localizablenodes. In order to change the density of nodes in the network, we adopt the way to adjust the communication radius of the node in the experiment. When the node communication radius changes in the [35, 55] range, in theG-shaped network, the variation range ofis 2.16 to 4.19; in the S-shape area, the variation range ofis 2.25 to 3.81; in theZ-shaped area, the variation range ofis 2.38 to 4.53. Fig. 11 shows the effects with differenton the localization performance.
In theory, with the increase of node communication radius, the number of neighbors would increase accordingly, and the per-hop-distance of nodes is closer to the actual distance. However, this is not the case in reality. As described in the literature [Lee and Kim (2011)], in the multi-hop network, the node distribution conforms to the Poisson distribution, and the increase of communication radius will not increase the estimation accuracy, but results in fluctuation. According to Fig. 11, we can find that although the estimation accuracy presents fluctuation with the change of communication radius R, no matter how the communication radiusRchanges, the proposed method in this paper is always superior to the DV-hop, Nearest-4, DV-Maxhop, LWLR-DV-hop, PDM, LSVR and LRR methods.

Figure 11: Simulation results of uneven node distribution with different radio range
6 Conclusions
A novel multi-hop algorithm for wireless network with unevenly distributed nodes is proposed in this paper. The proposed approach is based on the elastic net, which is a regularization method with good interpretability and stability. In the proposed meth-od,each unknown node estimates its location using the mapping model by elastic net constructed with anchor nodes. In this mapping model, the location of the unknown node is estimated by the information related to the minimum hops of the unknown node to all of the anchor nodes. The proposed approach is applicable to the scenarios where nodes are unevenly distributed. The experiment demonstrated the superior performance of the proposed approach compared to previous multi-hop localization methods in a variety of different distribution environments.
Acknowledgement:The paper is sponsored by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (15KJB520009, 16KJD520004), China Postdoctoral Science Foundation (2016M601861), Jiangsu Postdoctoral Science Foundation (1701049A), and the Open Project Program of Jiangsu Key Laboratory of Remote Measurement and Control (YCCK201603).
 Computers Materials&Continua2019年1期
Computers Materials&Continua2019年1期
- Computers Materials&Continua的其它文章
- A Co-Verification Interface Design for High-Assurance CPS
- A Robust Image Watermarking Scheme Using Z-Transform,Discrete Wavelet Transform and Bidiagonal Singular Value Decomposition
- A Fair Blind Signature Scheme to Revoke Malicious Vehicles in VANETs
- Development and Application of Big Data Platform for Garlic Industry Chain
- GA-BP Air Quality Evaluation Method Based on Fuzzy Theory
- Estimating the Number of Posts in Sina Weibo
