High Capacity Data Hiding in Encrypted Image Based on Compressive Sensing for Nonequivalent Resources
Di Xiao , Jia Liang Qingqing Ma Yanping Xiang and Yushu Zhang
Abstract: To fulfill the requirements of data security in environments with nonequivalent resources, a high capacity data hiding scheme in encrypted image based on compressive sensing (CS) is proposed by fully utilizing the adaptability of CS to nonequivalent resources. The original image is divided into two parts: one part is encrypted with traditional stream cipher; the other part is turned to the prediction error and then encrypted based on CS to vacate room simultaneously. The collected non-image data is firstly encrypted with simple stream cipher. For data security management, the encrypted non-image data is then embedded into the encrypted image, and the scrambling operation is used to further improve security. Finally, the original image and non-image data can be separably recovered and extracted according to the request from the valid users with different access rights. Experimental results demonstrate that the proposed scheme outperforms other data hiding methods based on CS, and is more suitable for nonequivalent resources.
Keywords: Compressive sensing, encrypted image, data hiding, prediction error,nonequivalent resources.
1 Introduction
There are many application scenarios in Internet of Things or Cloud Computing where different entities possess nonequivalent resources. For example, in wireless multimedia sensor networks (WMSNs), various nodes, such as common scalar sensors, multimedia sensors, multimedia processing hubs and sink, have different requirement about resources.Especially general sensors are typically resource- constrained devices which cannot afford a huge number of computation, while multimedia processing hubs and sink will have comparatively large computational resources [Akyildiz, Melodia and Chowdury(2007)]. Due to the resource limitation, there are lots of challenges in its corresponding security application [Li, Zhang, Chen et al. (2018)]. Fortunately, the emergence of compressive sensing (CS) opens up a new vision for multimedia data security with nonequivalent resource limitation.
CS has gained wide attention since it was introduced. CS can achieve compression and encryption together through matrix multiplication [Rachlin and Baron (2008)]. Compared with the stream cipher encryption, the encrypted data based on CS can reduce bandwidth resources effectively. Due to this feature of CS, research results based on CS often serve multimedia data compression and representation [Wu, Yu, Yuan et al. (2016)].Meanwhile, CS has a low computation cost in the sensing part while the computation of recovery is rather complex at the receiving end.
Information hiding plays an important role in protecting various information from being destroyed [Cao, Zhou, Sun et al. (2018)]. Within the current application of CS in reversible data hiding, there are two main types: the first one usually embeds data in the samples of DCT/DWT and then uses CS to compress [Xiao and Chen (2014)]. The other one embeds data in the measured value [Cao, Du, Wei et al. (2016); Li, Xiao and Zhang(2016); Pan, Li, Yang et al. (2015)]. However, both of the two schemes have some defects. The first one is more suitable for digital watermarking rather than data hiding,which focuses on the protection of the copyright about the carrier and the robustness of the watermark. But, data hiding puts more emphasis on the capacity and security of the embedded information itself. The scheme proposed by Pan et al. [Pan, Li, Yang et al.(2015)] is a watermarking scheme for plain image only which does not provide security for the cover. The scheme proposed by Cao et al. [Cao, Du, Wei et al. (2016)] is not suitable for nonequivalent resources, although this scheme has a brilliant performance on recovery. The reason is that sparse representation to vacate room for data embedding in the preprocessing operation is very complicated. The scheme proposed by Li et al. [Li,Xiao and Zhang (2016)] is a smart data hiding scheme based on block compressive sensing, but its capacity is limited by block size. To design a qualified hiding scheme in encrypted image based on CS for nonequivalent resources, the computational complexity in the sensing part should be focused on.
In this paper, we propose a high capacity data hiding scheme in encrypted image based on CS for nonequivalent resources. Multimedia sensor nodes take pretreatment on covers to vacate room and encrypt them by CS. General sensor nodes get non-image data, then encrypt them. Multimedia processing hubs gather data from sensor nodes and embed the encrypted scalar data into the processed image. Sink node is in charge of managing and processing data from hubs, and will extract the embedded data and recover image for the valid user with different access rights. Due to the properties of CS, the processes of encryption and embedding are simple and suitable for resources constrained device. This feature falls in with nonequivalent resources on this point while the process of embedding secret data into encrypted image can reduce the data transmission. The main advantages of our scheme include the adaptability to nonequivalent resources, the separable processing according to different access rights, the improvement of the embedding rate and the quality of recovery image.
The rest of this paper is organized as follows. Section 2 introduces the theory of CS.Section 3 provides detailed description of the proposed scheme. The experimental results and analysis are shown in Section 4. Finally, this paper is concluded in Section 5.
2 Compressed sensing


Then the matrix Φ satisfies the k-th order restricted isometry property (RIP). The matrix approximately preserves the distance between k vectors, and the sparse coefficients can be accurately reconstructed from the measurements. In the sampling process, one fact is that real world datamay not be always sparse. But as long as it can be represented as asparse vector α under some properly chosen sparse basiscan still use CS theory and have. Here, let, If matrixsatisfies RIP, then the sparsecould be recovered with high probability fromby solving an-minimization problem.

Rachlin et al. [Rachlin and Baron (2008)] pointed out that compressed sensing is computationally secure, although CS does not reach the perfect security definition of Shannon. So, CS can compress and encrypt when sampling. The standard CS can be interpreted as a symmetric encryption system where the original signalXis a plaintext,the measurementsYis a ciphertext, and the encryption algorithm is a linear transformation operated by a key which is a measurement matrix.
3 Proposed scheme
In this section, we present the detailed procedures of our scheme. As illustrated in Fig. 1,it involves five entities: multimedia sensor nodes, general nodes, multimedia processing hubs, sink nodes and valid users.
3.1 Image pretreatment and encryption
For an 8-bit grayscale image, let the pixel value at the position. As shown in Fig. 1, at the multimedia sensor nodes, the original image is first divided into two parts according to a checkerboard style. If the indicessatisfyis classified intopart. And the rest pixels infall intopart.


Figure 1: The flow chart of the proposed scheme



Next, pseudo-random bits are padded in front ofhave the same size withand the number of padded bits is the embedding capacity which is determined by the compression ratio. The last step is to embed the embedding capacity in the first three positions of, as the front ofis vacated for data embedding.
Finally, the encrypted image with vacated room,, is generated by restoring the corresponding position ofin the checkerboard, wherecan be considered as the encryption key.
3.2 Message encryption
General sensor nodes gain other types of datasuch as temperature, humidity and position. For security, these data need to be encrypted as well. Here, a standard stream cipher is used to encrypt the data intoby bitwise exclusive-or operation with a pseudo-random bit sequence generated by the key. This process is similar to Eq. (5).
3.3 Data hiding in the encrypted images
At the multimedia processing hubs, the encrypted image should be partitioned intoandat first, and the embedding capacity is extracted from the first three positions inThen, the encrypted datais embedded intoby replacing the former padded pseudo-random bits. As the data is embedded in the front ofif image is directly restored according to the corresponding location, the embedded data will be in dangerous.In order to improve the security, the block with embedded data,, will be lightly encrypted intoby digitized Arnold transform:

3.4 Data extraction and image recovery
Sink node will extract data and restore image accordingto the request from valid users with different access rights.
If valid user can access comprehensive data including image and embedded data, sink node will recover image, extract embedded data and send them to user by both data hiding key and encryption key. The processes in the extracting and recovering are the inverse of data embedding and image encryption, so they are not elaborated here. CS reconstruction is a solution of the minimalnorm [Donoho (2006)].
In the second case, if the valid user can only access embedded data, sink node will extract data by the hiding key and deliver it to user.
In the third case, if the valid user can only access approximate image, sink node will decrypt thepart inby the encryption key and then provide an approximately recovered image without embedded data through interpolation.
For the latter two cases, the resource consumption can be effectively reduced because CS reconstruction is not in need.
4 Experimental results and analysis
In this section, eight 512×512 standard images, including Lena, Cameraman, Baboon,Barbara, Boat, Plane, Peppers and Mondrian, are used in the experiment. Besides, another test image set containing 100 images is formed by randomly selecting from Corel database which is available from CorelDraw version 10.0 software. And the selected image is cropped to 512×512 pixels and turned into grayscale. The prediction error is calculated by interpolation technique. The sampling operator is scrambled dense FFT[Candes and Romberg (2006)]. The sparsifying transform is the 9-7 wavelet transform used in the JPEG 2000 standard and the optimizer is based on the GPSR program[Figueiredo, Nowak and Wright (2008)].
4.1 Evaluation of the proposed scheme
In our scheme, the vacated room for embedding data is obtained by CS. Therefore, the embedding rate is directly related to the compression rate of CS onpart in Fig. 1. Since only half of each image is processed by CS, for an 8-bit gray image, the relation is


Table 1: The relation between embedding rate and compression rate
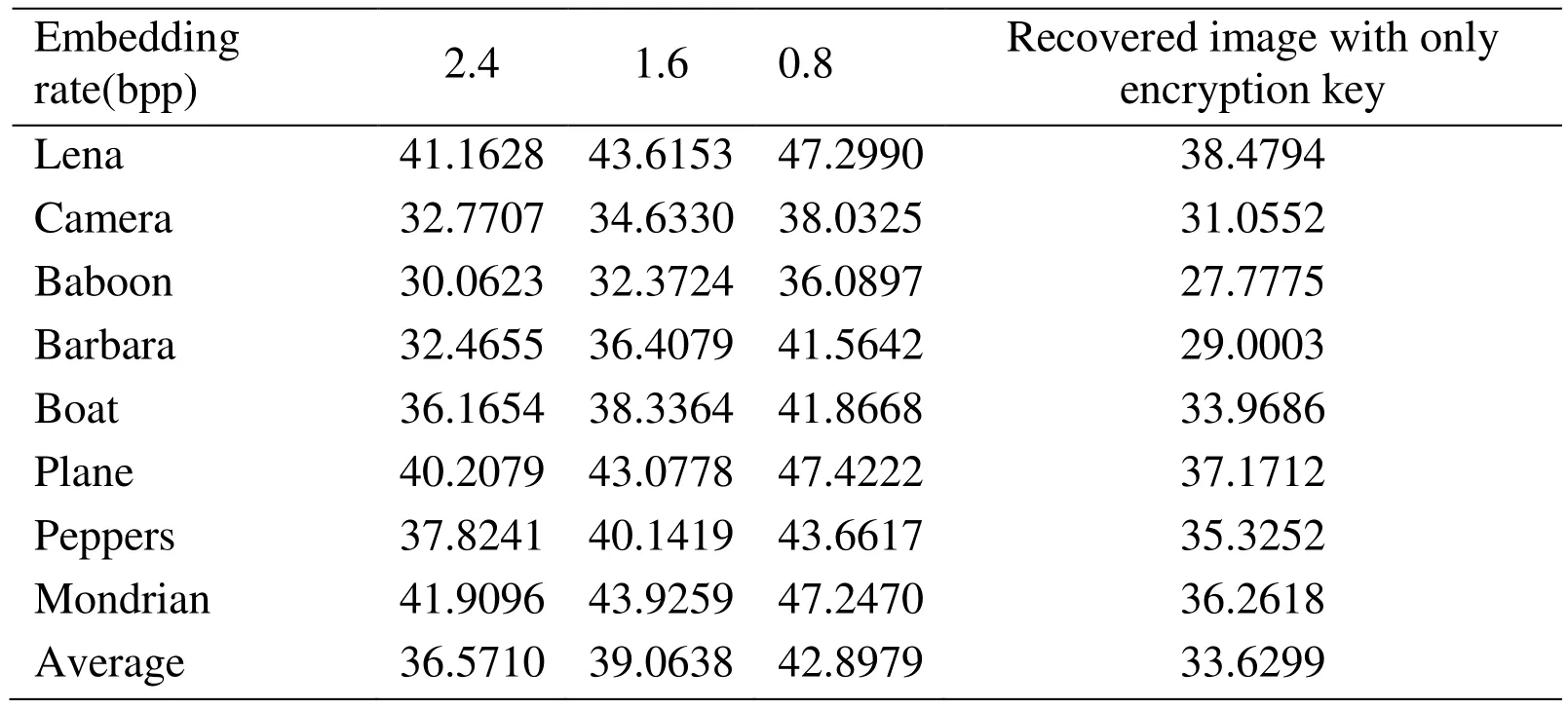
Table 2: PSNR(dB) with different embedding rates for different test images
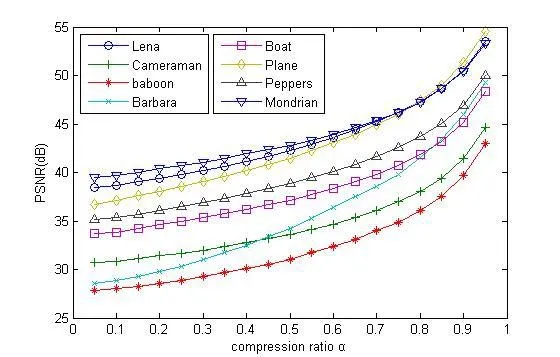
Figure 2: Relationship between compression ratio and PSNR
In the schemes of data hiding in CS domain, both the cover data (sparse samples) and the embedded data are exactly recovered under certain noise, payload and sparsity conditions,so these methods can be qualified as conditionally reversible data hiding [Yamaç, Dikici and Sankur (2016)]. In our scheme, CS is the only part of the whole process that will bring the loss, and the sensing object of CS is the prediction error. The accuracy of part,the first half of the original image, is ensured; while the other half of the original image,part, can be recovered based on both the interpolation technique and the prediction error reconstructed by CS. As a result, the proposed scheme has a good recovery performance.This can be seen in Fig. 2, Fig. 3 and Tab. 2. When the compression rate is significantly low, the quality of the full recovery image is close to the one using interpolation technique only. Of course, the higher the compression rate is, the smaller the error of CS reconstruction is, and the quality of recovery image will be higher. When the compression rate approaches 0.95, the PSNR values of the full recovery image are greater than 43, and may even be close to 55.

Figure 3: The PSNR under different ER values
It should be noted that the computation in the encryption and embedding processes of the proposed scheme is relatively low because there are only arithmetic and matrix multiplication. And in the process of image recoveryoptimization problem is a relatively complex operation. Meanwhile, since this is a high capacity scheme, other types of non-image data and part of image data can be embedded into the cover image to reduce the transmission consumption. The comprehensive data collected in the same area can be considered as the properties of the region and has its special usage. In our scheme,the obtained comprehensive data, including the encrypted non-image data and image in the same area, can not only ensure the data security, but also be convenient for data management.
Therefore, the scheme is suitable for the applications with nonequivalent resources.
4.2 Performance comparison
When compared with other schemes based on CS, it can be seen from Fig. 4 that the proposed scheme has a better recovered image performance when using the same compression ratio for the whole image. In Fig. 4, the abscissa indicates the compression ratio, and the ordinate indicates the PSNR value of the recovered image. The reason is that only half of the data in the original image is processed and compressed by CS, and the other half is processed by the conventional stream cipher. Therefore, the quality of the restored image is ensured to be significantly better than other schemes based on CS.
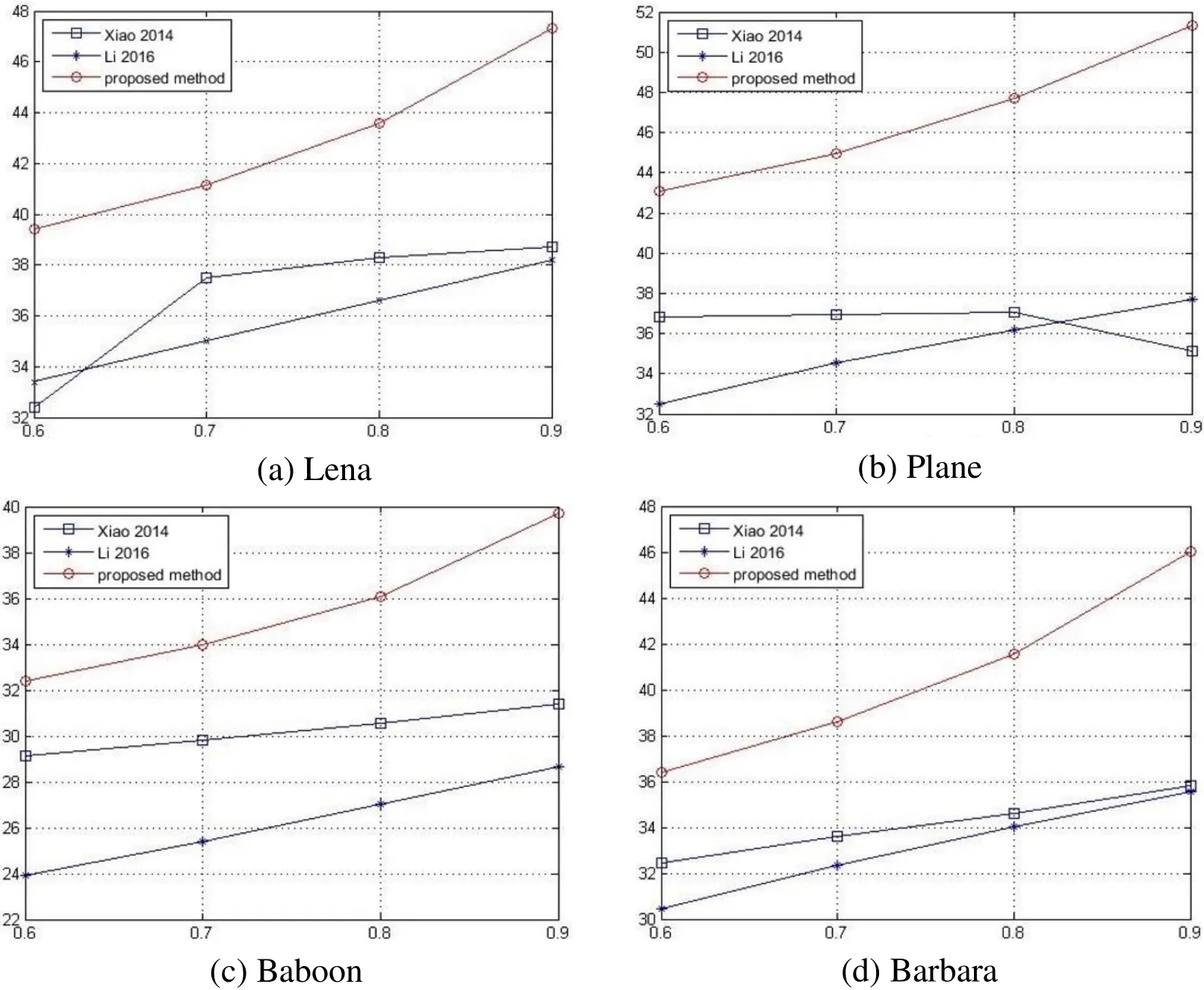
Figure 4: Comparison results of the same compression ratio
Moreover, we make a comprehensive comparison among our scheme and some typical data hiding schemes based on CS in Tab. 3. According to Eq. (9), the maximal theoretical embedding rate of the proposed scheme is 4 bpp, and we calculate the average PSNR values of the recovered Lena under different embedding ratios for different schemes. It should be noted that although the title of the scheme proposed by Li et al. [Li, Xiao and Zhang (2016)] contains “reversible data hiding”, it is not a lossless scheme, so its PSNR is not infinite. Based on Tab. 3, the proposed scheme has the largest theoretical capacity so that the embedding rate can be adaptively adjusted according to different requirements.
At the same time, the quality of recovered image is only worse than he scheme proposed in Cao et al. [Cao, Du, Wei et al. (2016)]. However, since the background of our scheme is resource deficient device, we need to focus on the computational complexity about image pretreatment and encryption (as the embedding operation is relatively simple, and the data extraction side has more resources for complex calculation). According to the scheme proposed in Cao et al. [Cao, Du, Wei et al. (2016)], its computational complexityis the image size,is the number of dictionary atomsis the nonzero element number in each coefficient vector,andis the embedding round number. Meanwhile, the computational complexity of our scheme iscorresponding to the three main processes: stream encryption, prediction error estimation and CS, whereis the image size, andis the row number in measurement matrix. In this aspect, our scheme is more suitable for nonequivalent resources than the scheme proposed by Cao et al [Cao, Du, Wei et al.(2016)].
All in all, the proposed scheme is a high capacity data hiding scheme which is more suitable for resource-constrained devices and has a better performance while comparing with other existing schemes.
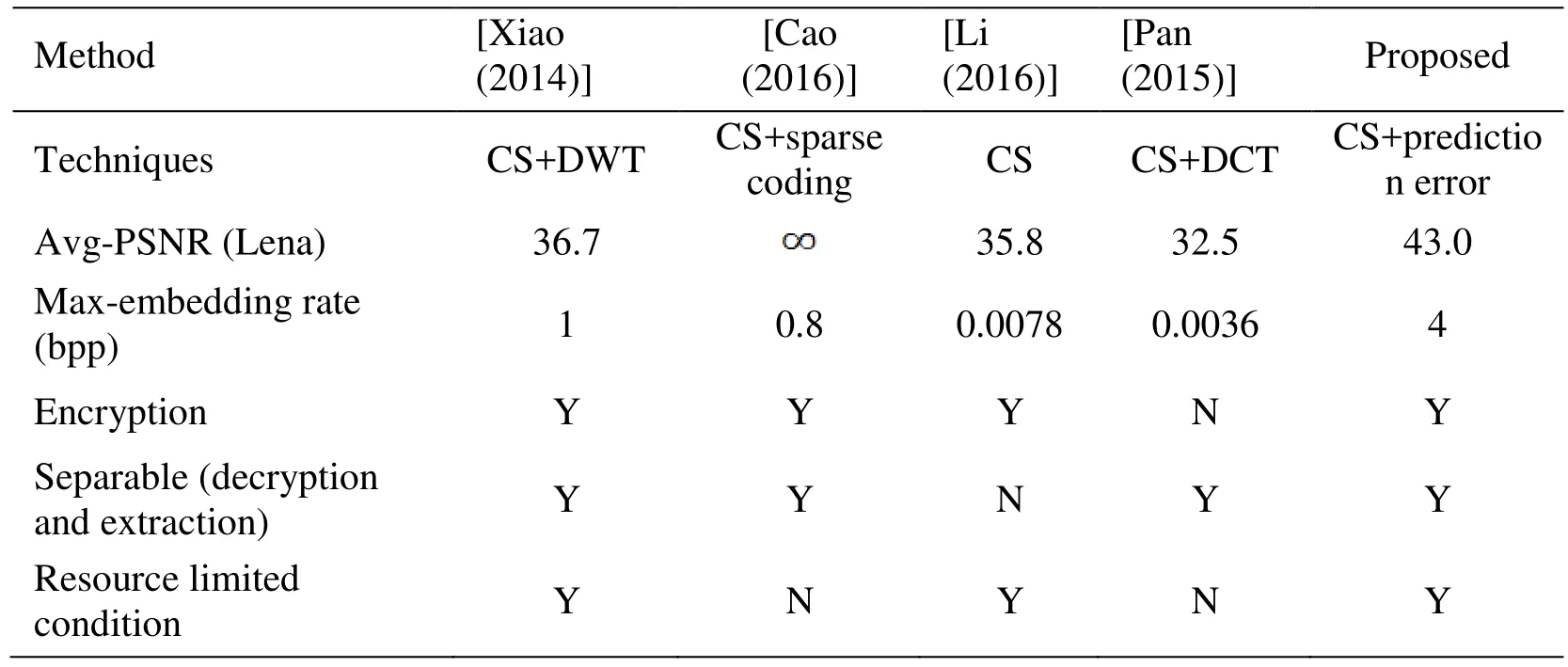
Table 3: Performance comparison
4.3 Security of encrypted image
In this section, we will discuss the security of the encrypted image in the proposed method.
The natural images pixels are highly correlated. A qualified encryption algorithm must break the correlation between adjacent pixels to resist statistical attack. A correlation coefficient value “one” represents a highly correlated image which is susceptible to statistical attacks. Correlation Coefficient (CC) is given by


Table 4: Correlation Coefficient (CC) and SSIM
The randomness of the image is measured by Entropy as

For an image with 256 grey levels the absolute maximum of entropy is 8 bits per pixel.The maximum entropy is obtained when the gray levels have equal probability of occurrence. Hence for a cipher image, the entropy value should be close to 8. From Tab.5, we can infer that the lower the compressionofDpart, the greater the entropy.The encrypted image has high randomness as the entropy of cipher is close to the theoretical value of 8.
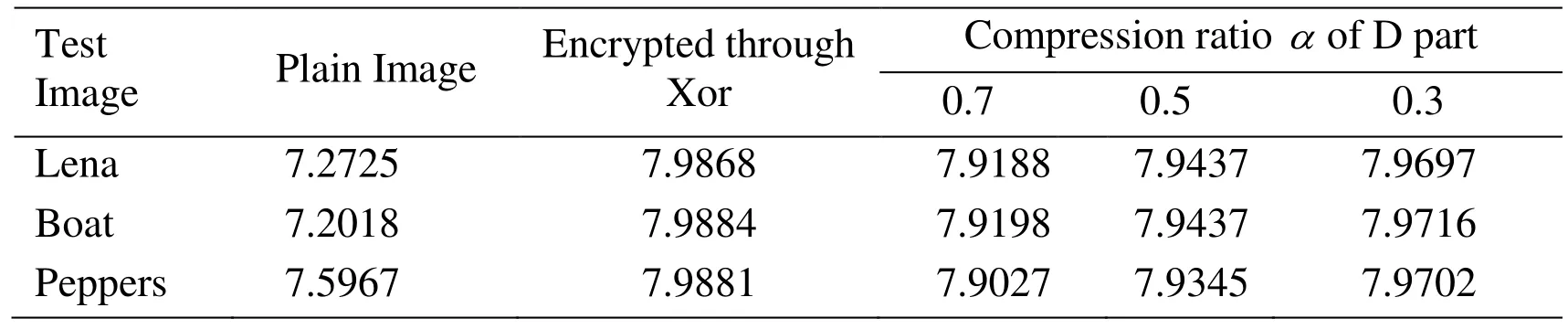
Table 5: Entropy of encrypted image
5 Conclusion
In this paper, a high capacity data hiding scheme in encrypted image based on CS is proposed. In this scheme, image decryption and data extraction are separable to match the requests of the users with different access rights. The experimental results have demonstrated that it performs well in the tradeoff between the embedding rate and the recovered image quality. Compared with other data hiding schemes based on CS, the proposed one is much more suitable for nonequivalent resources. In our future study, a part of image may be embedded into other image data to further reduce the transmission consumption.
Acknowledgement:The work was funded by the National Natural Science Foundation of China (Grant Nos. 61572089, 61502399, 61633005), the Chongqing Research Program of Basic Research and Frontier Technology (Grant No. cstc2017jcyjBX0008),the Project Supported by Graduate Student Research and Innovation Foundation of Chongqing (Grant No. CYB17026), the Chongqing Postgraduate Education Reform Project (Grant No. yjg183018), the Chongqing University Postgraduate Education Reform Project (Grant No. cquyjg18219) and the Fundamental Research Funds for the Central Universities (Grant Nos. 106112017CDJQJ188830, 106112017CDJXY180005).
 Computers Materials&Continua2019年1期
Computers Materials&Continua2019年1期
- Computers Materials&Continua的其它文章
- A Co-Verification Interface Design for High-Assurance CPS
- A Robust Image Watermarking Scheme Using Z-Transform,Discrete Wavelet Transform and Bidiagonal Singular Value Decomposition
- A Fair Blind Signature Scheme to Revoke Malicious Vehicles in VANETs
- Development and Application of Big Data Platform for Garlic Industry Chain
- GA-BP Air Quality Evaluation Method Based on Fuzzy Theory
- Estimating the Number of Posts in Sina Weibo
