基于GM(1,1)模型的贫信息渔业数据CPUE标准化研究

杨胜龙，张 禹，戴 阳，李灵智，汤建华，张 勋，张忭忭

(1. 上海海洋大学海洋学院，上海 201306；2. 中国水产科学研究院东海水产研究所、农业部远洋与极地 渔业创新重点实验室，上海 200090; 3. 江苏省海洋水产研究所，江苏 南通 226007)

长期以来我国近海海洋捕捞面临渔船数量多、捕捞强度大的问题.随着我国海洋渔具管理制度的日益完善、渔具准入制度的深入推进，在控制渔船总量及海洋捕捞总产量的情况下，渔具作为最直接的捕捞工具，有必要对渔具使用数量、渔具捕捞努力量进行控制，海洋捕捞的可持续发展目标才能实现.为了降低海洋捕捞对海洋生态系统的影响，将海洋捕捞渔具使用数量合理控制，是控制捕捞努力量的关键.单位捕捞努力量渔获量(catch per unit of effort，CPUE)标准化是渔业资源评估和管理基础性工作[1-2]，是制定合理捕捞计划的支撑.国内外学者在CPUE标准化方面做了大量研究工作[3-10]，发展了不同的数学模型，先后采用广义线性模型(generalized linear model, GLM)[2]、广义叠加模型(generalized additive model, GAM)[2]、人工神经网络(artificial neural network, ANN)[6]、回归树模型(regression trees, RT)[7-8]、随机森林(random forest, RF)模型[9]和支持向量机(support vector machine, SVM)[10]等模型用于CPUE标准化.上述渔业CPUE标准化方法数学原理是建立名义CPUE对自变量(时空变量和环境变量)的回归模型.

在实际中，许多采集和统计的调查监测数据没有空间变量和环境变量，同时渔业管理单位监测采集和统计的调查生产数据存在信息量少，而且有缺失的问题.这种渔业数据无法用前述的模型方法建立因变量和自变量响应关系模型进行CPUE标准化工作.在实际工作中，必须依据该数据支撑渔业管理部门的决策，因此针对这种情况必须提出新的CPUE标准化方法.

灰色系统理论是一种研究少数据、贫信息不确定性问题的方法，以“部分信息已知，部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象，主要通过对“部分”已知信息的生成、开发，提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控[11].灰色建模的优点是要求的样本点少,不必有较好的分布规律，已经被广泛应用于工业、农业、交通、物流等社会经济领域[12].本研究采用灰色预测GM(1,1)模型对信息量少的渔业调查数据进行CPUE标准化研究，为渔业管理部门提供决策支持.

1 材料方法

1.1 模型及检验方法

1.1.1 灰色GM(1,1)模型 灰色系统中建立的模型称为灰色模型(grey model,GM),该模型是以原始数据序列为基础建立微分方程，利用系统信息对抽象的模型量化，进而在缺乏系统特性知识的情况下预测系统输出.设时间系列有n个观测数据x(0)=x(0)(1),x(0)(2),…,x(0)(n)，通过一次累加生产新的数据系列x(1)=x(1)(1),x(1)(2),…,x(1)(n).这个新的数据系列，其变化趋势可以近似地用如下微分方程描述：

(1)

式(1)中：a称为发展灰数，b称为内生控制灰数.β=(a,b)T可以通过如下的最小二乘法拟合得到：

(2)

式(2)中：

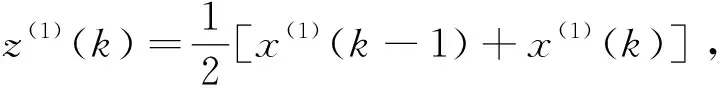
x(1)(k)+a·z(1)(k)=b

(3)

微分方程(2)为灰色微分方程(3)的白化方程，也称影子方程.

① 白化方程的解也称时间响应函数，其为：

(4)

② GM(1,1)灰色微分方程x(1)(0)+a·z(1)(k)=b的时间响应函数系列为：

k=1,2,…,n

(5)

取x(1)(0)=x(1)(1)，有

(6)

③累减后的预测方程为：

(7)

k=1,2,…,n

GM(1,1)模型的适用范围:

① 当-a≤0.3时，GM(1,1)模型的一步预测精度在98%以上，三步和五步预测精度都在97%以上，可用于中长期预测.

② 当0.3<-a≤0.5时，GM(1,1)模型的一步和二步预测精度在90%以上，十步预测精度都在80%以上，可用于中短期预测.

③ 当0.5<-a≤0.8时，用于短期预测应十分慎重.

④ 当0.8<-a≤1.0时，GM(1,1)模型的一步预测精度已低于70%，应采用残差修正模型.

⑤ 当a>1.0时，不宜采用GM(1,1)模型.

1.1.2 检验方法 灰色预测检验一般分为残差检验、关联度检验和后验差检验.

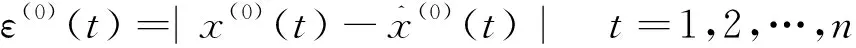
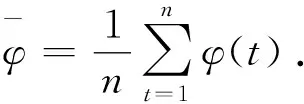
② 关联度检验.通过考察模型值曲线与建模系列曲线的相似程度进行检验.

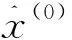
③ 后验差检验.对于预测公式，我们所关心的是它的预测精度.这一预测公式是否达到精度要求，可按下述方法进行精度检验.

首先计算原始系列平均值：

(8)

第二步计算原始系列标准差：

(9)

第三步计算绝对误差系列的标准差：

(10)

第四步计算方差比：

(11)

最后计算小误差概率：

(12)

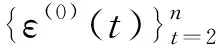
本研究采用上述残差检验、关联度检验和后验差检验方法检验建立的CPUE标准化模型精度.

1.2 渔业数据

本研究渔业调查数据来源于2010—2014年江苏省沿海4种张网类调查渔船生产数据，数据包含年、月、网次和总产量.其中单锚张纲张网监测船2艘，年平均有效监测网次约为2 000网次，5a共46条数据记录；单桩桁杆张网监测船1艘，年平均有效监测网次2 366网次，5a共41条数据记录；双桩竖杆张网监测船2艘，年平均有效监测网次约为3 889网次，5a共38条数据记录； 多锚单片张网监测船2艘，年平均有效监测网次约为2 500网次，5a共20条数据记录.4种张网每年调查月份和次数不一致，而且没有空间和环境变量信息.

统计计算4种网次监测数据和所有数据的年平均名义CPUE(kg/网)，CPUE计算公式如下:

CPUE=Ca/Ne

(13)

式(13)中：Ca是当年某种网次或所有网次的总的调查渔获量(kg)，Ne是当年某种网次或所有网次的总的作业网次.

按式(11)计算的年平均名义CPUE见表1.结合计算的年平均名义CPUE值，采用GM(1,1)分别对单桩桁杆张网、单锚张纲张网、双桩竖杆张网和所有网目数据建模CPUE标准化模型.多锚单片张网2012年缺失数据，而且时间序列较短，因此文章不单独建立CPUE标准化模型.

表1 各种张网调查数据年平均名义CPUE(kg/网)Tab.1 Annual average nominal CPUE from data obtained from different stow nets

2 结果与讨论

2.1 CPUE分布图

采用GM(1,1)建模(表2)对原始名义CPUE进行累加.单桩桁杆张网(图1a)、单锚张纲张网(图1b)、双桩竖杆张网(图1c)和所有网目数据(图1d)名义CPUE和累计数列见图1.
图1表明单桩桁杆张网、单锚张纲张网、双桩竖杆张网和所有网目数据原始的名义CPUE呈现为不平稳的随机数列，表现为无规律的波动，其发展无规律可循.累计叠加后的新数列随机性程度大大弱化，平稳度也大大增加，其变化趋势可以近似的用微分方程描述.

2.2 灰色GM(1,1)模型参数

采用GM(1,1)分别对单桩桁杆张网、单锚张纲张网、双桩竖杆张网和所有网目数据建模CPUE标准化模型，模型参数见表2.单桩桁杆张网的灰色GM(1,1)模型的发展灰色(a)绝对值小于0.5，可以用于中短期预测.单锚张纲张网、双桩竖杆张网和所有网目数据的灰色GM(1,1)模型的发展灰色均小于0.3，可以用于中长期预测.

表2 GM(1,1)模型Tab.2 Model for GM(1,1)

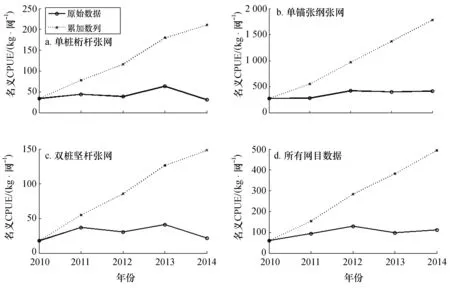
图1 2010—2014年名义CPUE和累计数列图Fig.1 Annual average nominal CPUE of 2010-2014 and the chart of accumulative series

2.3 名义CPUE和标准化CPUE比较

2000—2014年, 灰色GM(1,1)模型计算的标准化CPUE和名义CPUE年平均走势见图2. 单桩桁杆张网(图2a)、单锚张纲张网(图2b)、双桩竖杆张网(图2c)和所有网目数据(图2d)的标准化CPUE和名义CPUE年分布趋势均完全不一样.4种数据的名义CPUE时间序列无规律波动，但标准化后的CPUE时间序列平稳度也大大增加，时间序列变化趋势明显.单桩桁杆张网和双桩竖杆张网的标准化CPUE在2010—2011年快速递增，2011年之后缓慢递减.单锚张纲张网的标准化CPUE一直呈现线性递增趋势.所有数据标准化CPUE在2010—2011快速递增，2011年之后呈现非常缓慢的线性递增趋势.

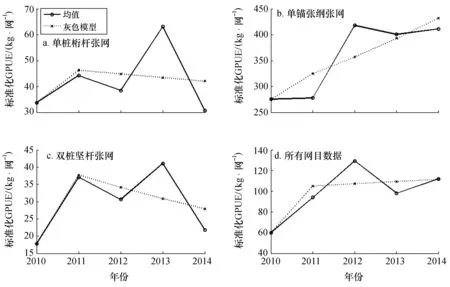
图2 灰色GM(1,1)模型计算的CPUE和名义CPUE年平均图Fig.2 Comparisons of annual average nominal standardized CPUE and calculated CPUE by the grey GM(1,1) method

2.4 灰色GM(1,1)模型精度

表3 单桩桁杆张网残差检验Tab.3 Residual test for single stake two-stick swing net

单锚张纲张网残差检验见表4.关联度r=0.623，在λ=0.5条件下，满足检验准则，检验为满意.后验差计算的c=0.35、p=1.0，根据灰色预测精度检验等级表，模型预测等级为好.

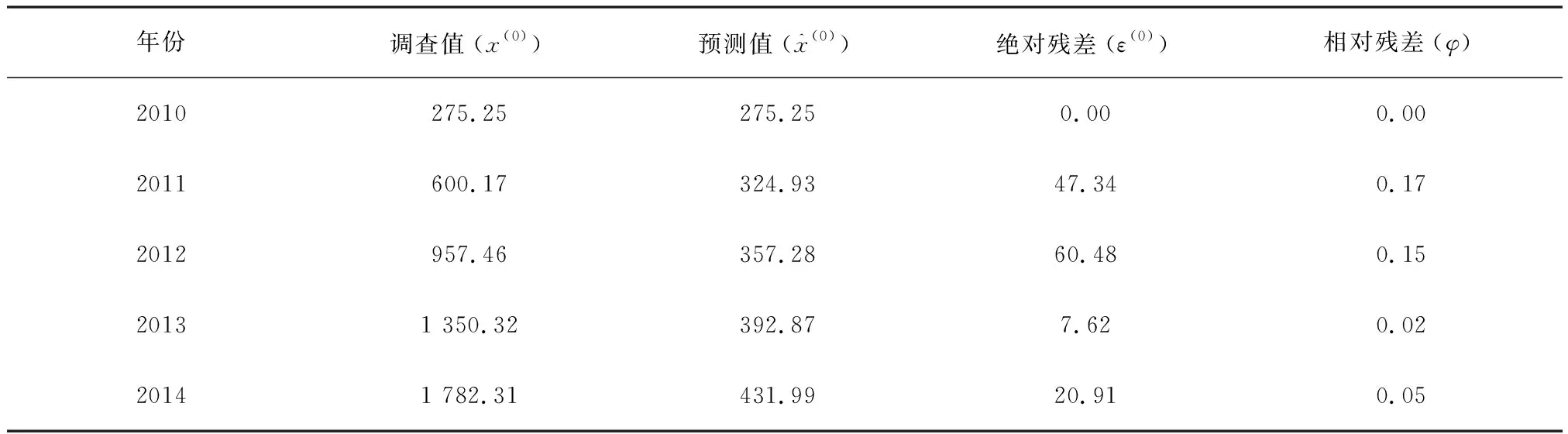
表4 单锚张纲张网残差检验Tab.4 Residual test for canvas stow net

双桩竖杆张网残差检验见表5. 关联度r=0.65，在λ=0.5条件下，满足检验准则，检验为满意.后验差计算的c=0.43、p=1.0，根据灰色预测精度检验等级表，模型预测等级为好.

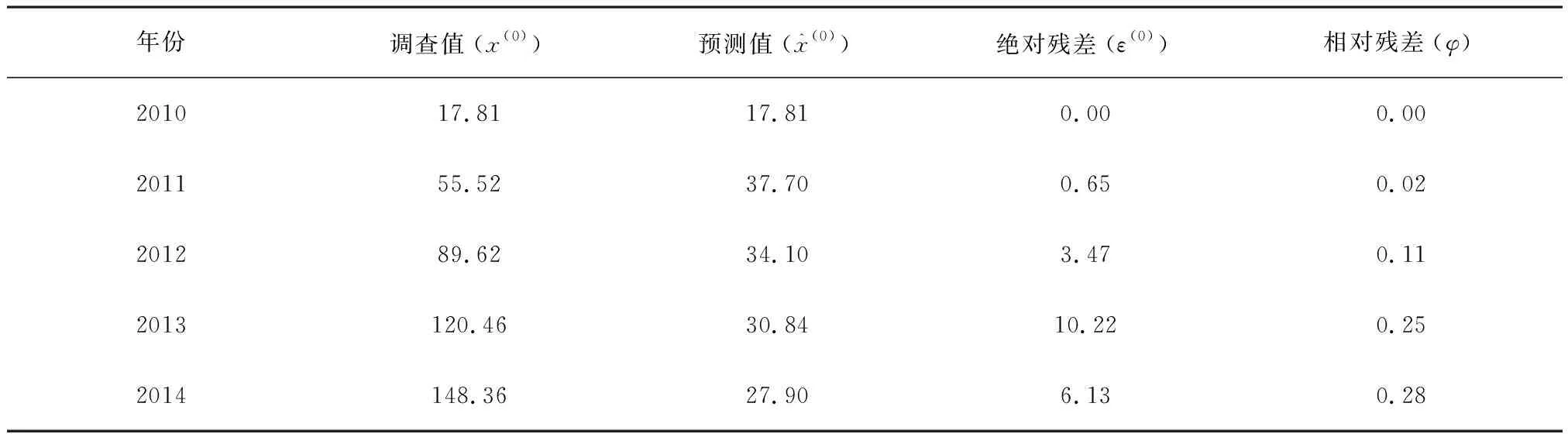
表5 双桩竖杆张网残差检验Tab.5 Residual test for two stake two-stick stow net

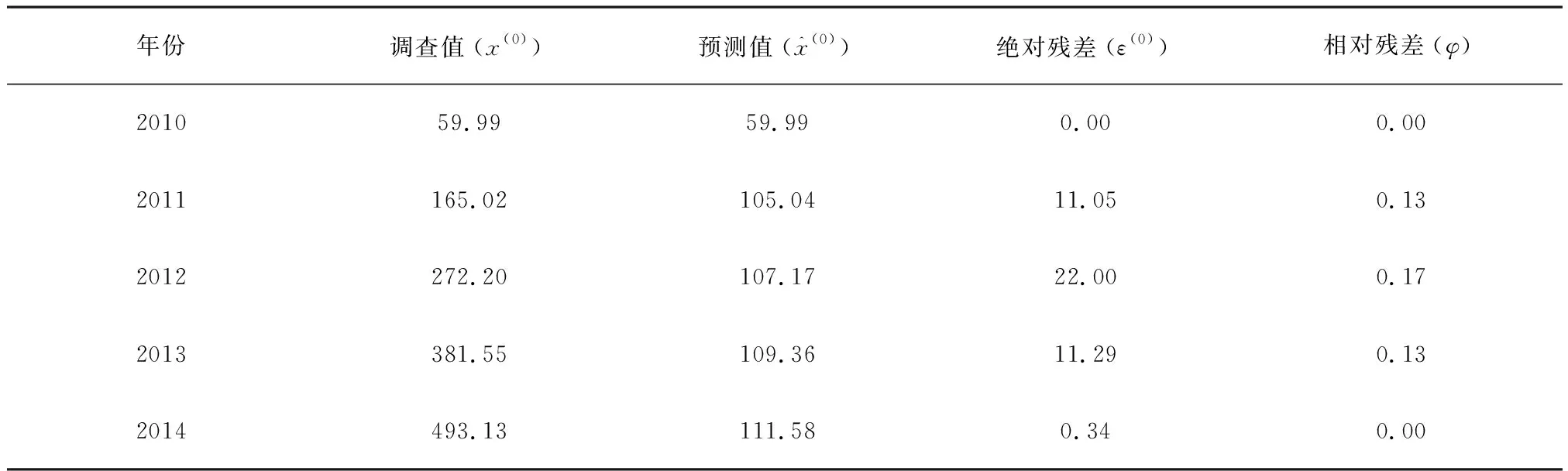
表6 所有网目数据残差检验Tab.6 Residual test for all stow nets

2.5 讨论

2.5.1 模型精度 传统统计方法和新的机器学习方法被广泛的应用于数据渔业CPUE标准化，其原理是建立名义CPUE作为和各种输入变量(时空变量和环境变量)的回归模型.本研究的4种张网调查数据只有渔获率、时间和网次记录，无法采用统计方法、机器学习方法进行标准化工作.而且4种张网每年调查月份和次数不一致，不具有时间序列特征.本研究采用灰色GM(1,1)模型，建立了没有空间变量和环境变量条件下的渔业CPUE标准化模型.模型的精度检验结果表明，所有模型的误差都可以接受(表3～6)；在关联度检验下，所有灰色GM(1,1)模型的关联度大于0.6，建模结果为满意；后验差结果显示所有灰色GM(1,1)的预测精度为合格.综合上述，本研究采用灰色GM(1,1)模型对信息量少、没有空间和环境信息的渔获数据进行CPUE标准化是可行的.模型的发展灰色表明本研究建立的4个CPUE标准化模型可以对未来几年的年平均CPUE进行有效的预测.预测的数据可以为渔业管理部门制定当年捕捞量计划提供科学支撑，或者在总的捕捞产量控制指标下，评估容纳量，制定不同围网作业方式当年可捕捞网次.

2.5.2 调查船数量对CPUE标准化影响 姜汶泉等(2008)研究表明[13]，随着采用的监测隧道样点的增加，GM(1,1)模型预测数据与原始数据之间的平均相对误差不断减小，即预测精度不断提高.本研究4种数据建立的灰色GM(1,1)模型精度有差异.所有数据建立的灰色GM(1,1)模型检验结果最好，是4种检验方法都是最优的，其次是基于单锚张纲张网，而基于单桩桁杆张网在4种数据种最差.2010—2014年期间，单桩桁杆张网、单锚张纲张网和双桩竖杆张网各自的调查船数量分别是1、2、2艘，历年累积调查作业次数分别是41、46、38次.在累积调查作业次数相近的情况下，不同模型的精度差异可能也是由于监测船的个数引起.监测船数量少的调查渔获信息显然具有更大的随意性和偶然性，而渔船数量多的数据，如所有网目数据，其平均后的CPUE值随意性和偶然性会降低.虽然灰色系统理论是一种研究少数据、贫信息不确定性问题的方法.在建模过程中，数据本身包含的随意性和偶然性还是会对模型的建立有影响.

2.5.3 空间分布对CPUE分布趋势的影响 3种张网数据标准化后的CPUE时间序列平稳度也大大增加，时间序列变化趋势明显(图2).所有标准化CPUE在2011年都快速上升，之后随着年份呈现不同发展趋势.单桩桁杆张网和双桩竖杆张网的标准化CPUE在2011年之后缓慢递减.单锚张纲张网的标准化CPUE一直呈现线性递增趋势.所有数据标准化CPUE在2011年之后呈现非常缓慢的线性递增趋势，几乎不变.标准化后的CPUE不同时间分布趋势，可能与不同张网作业水域及水域资源量有关.单锚张纲张网作业水域深，靠近外海；而单桩桁杆张网和双桩竖杆张网作业水域浅，靠近沿岸.标准化后的CPUE年分布趋势表明靠近沿岸的渔业资源丰度在缓慢减少，距离海岸较远的深水区域渔业资源密度有所增加.这与实际捕捞中，近海渔民更多的向外海作业现象吻合，而近海渔业资源显示越来越难捕获鱼类.

3 结论

本研究采用灰色预测GM(1,1)模型对信息量少的渔业调查数据建立了CPUE标准化模型.模型的残差在可以接受范围；关联度检验结果为满意；后验差预测精度为合格.因此，本研究采用灰色GM(1,1)模型对信息量少、没有空间和环境信息的渔获数据进行CPUE标准化是可行的.