GGQ 水电站重力坝坝基扬压力监测成果分析

方 晗，陶兴阳

(华能澜沧江水电股份有限公司,云南 大理 672700)

1 工程概况及扬压力监测布置情况

GGQ 水电站于云南省大理市，为二等大（2）型工程，电站枢纽工程由挡水建筑物、河床坝身泄洪建筑物、右岸地下引水发电系统组成。挡水、泄洪、引水及发电等永久性主要建筑物为2 级建筑物，次要建筑物为3 级建筑物。坝体类型为碾压混凝土重力坝，最大坝高105.0 m，坝体从左到右分为17 个坝段。共设5 个溢流表孔，布置在8 号～12 号坝段，有1 个泄洪底孔，设置在13 号坝段，剩余1 号～7 号、14 号～17 号坝段分别为左岸、右岸非溢流坝段。

钻孔布置测压管用于坝基扬压力监测，测压管钻入基岩深度1 m。将渗压计安装在测压管中，并连接至安全监测自动化系统，同时在廊道内安装压力表用于人工读数。沿坝轴线方向自上游至下游分别设置了第一排基础灌浆廊道、第二排纵向排水廊道、第四排排水廊道3 个监测断面，各断面上每个坝段有一个测点。垂直坝轴线方向选取了3 个典型坝段作为监测断面，包括5 号坝段、8 号坝段和14 号坝段中线，各个断面从上游帷幕前开始沿线布置测压管或渗压计。

2 监测成果定性分析

（1）首先绘制每个扬压力测点的测值过程线，从图中可以清楚地看到第一排基础灌浆廊道内扬压力测孔水位主要受上游水位变化影响，第四排排水廊道内扬压力测孔水位主要受下游水位变化影响。两排廊道内扬压力测值都随着水位升高而增大，水位下降而减小，呈现正相关关系，但也有一滞后过程。

（2）为分析上游主帷幕的防渗效果，计算2018 年6 月16日第一排基础灌浆廊道上各测点的实测扬压力系数见表1。除了位于6 号坝段的UP09 外，第一排基础灌浆廊道内的测点实测扬压力系数为0.01～0.17，均小于设计折减系数0.2，由此可以推断出大坝主防渗帷幕起到了良好的防渗作用，有效保障了大坝安全，实现了设计预期效果。

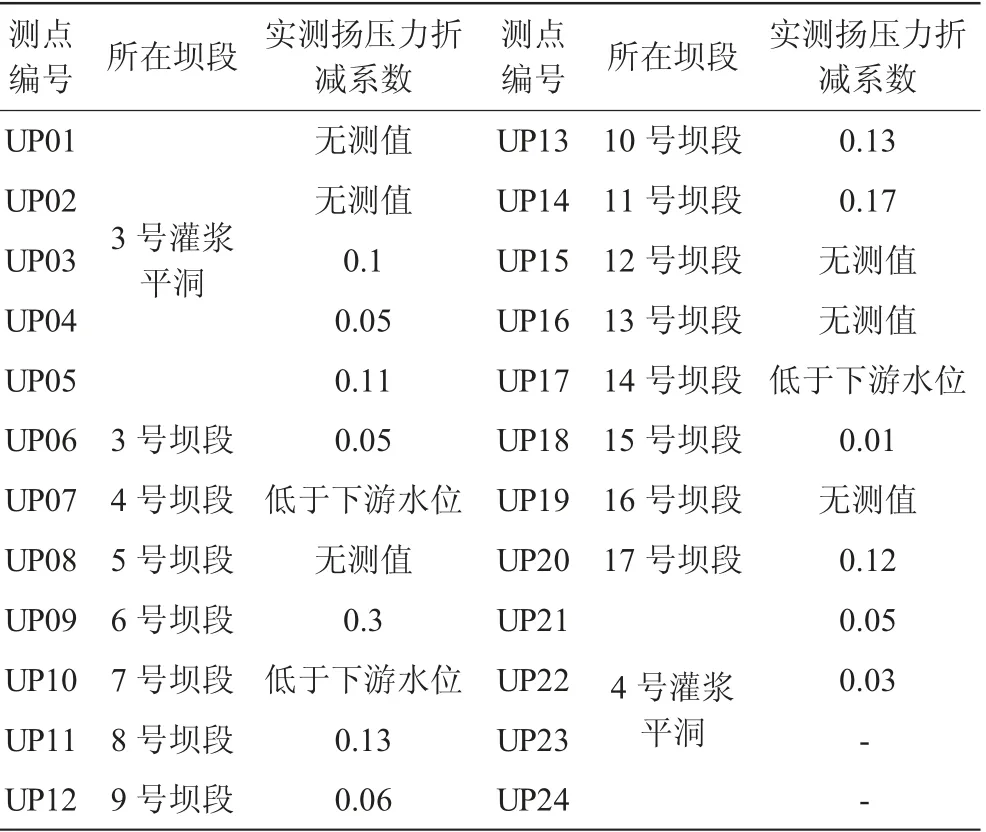
表1 第一排基础灌浆廊道扬压力折减系数表

（3）第一排基础灌浆廊道内6 号坝段UP09 测点的扬压力折减系数为0.3，显著高于第一排廊道位置设计扬压力折减系数0.2。经查阅地质资料，F25 断层通过该点位置，虽然断层已经过处理，但该测点可能正好位于破碎裂隙位置，导致扬压力测值偏高。经与同断面及附近测孔水位比较，可判断属于个别现象，不影响整个主帷幕防渗效果。现场检查发现距该点0.5 m有一个坝基排水孔，孔口无水，也能够佐证这一点。

（4）8 号坝段为最大坝高坝段，选取该坝段横向监测断面上从上游至下游的4 个扬压力测点，分别计算其换算水位见表2。由于下游水位较高，加上第四排排水廊道与上游防渗帷幕距离较远，因此第四排排水廊道内扬压力测孔水位受下游水位影响较大，说明设置下游帷幕是必要的。经计算，虽然UP39 测孔水位相对较高，但残余扬压力系数也未超出设计值0.5，不影响坝基安全。

表2 8 号坝段扬压力测孔水位表

3 监测成果定量分析

3.1 统计模型

使用逐步回归分析法[1]，利用扬压力测孔水位主要受上下游水位、温度、时效影响的原理，根据统计模型公式建立了46个坝基扬压力测点的回归模型。

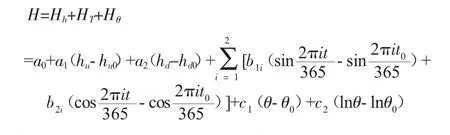
式中：a0、a1、a2、b1i、b2i、c1、c2为回归系数；Hu、hd为分别为对应日期的上游水深、下游水深；Hu0、hd0为分别为初始监测日上游水深、下游水深。t 为监测日至始测日的累计天数；t0为计算时段起测日至始测日之间的累计天数；θ 为监测日至测点始测日的累计天数除以100；θ0为建模起始日至始测日的累计天数除以100。

用于评估回归方程的有效性和精度的常用指标有复相关系数、标准差等[2]，因此，统计计算各测点数学模型回归方程的复相关系数见表3。可以看出，46 个测点中复相关系数大于0.8 的共有29 个测点，且最小复相关系数为0.68。结果表明，该统计模型具有较高的精度，可用于扬压力监测数据的定量分析。

表3 扬压力测点回归模型复相关系数统计表

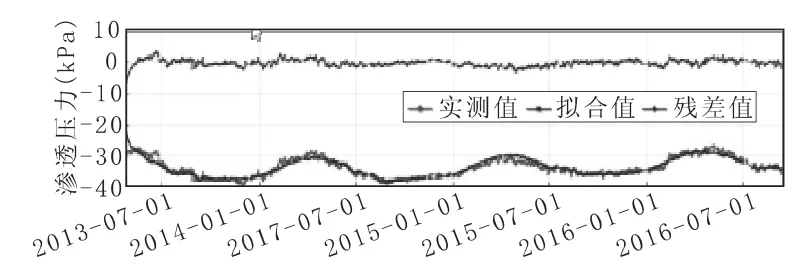
图1 UP06 实测拟合对比曲线图

3.2 影响因素分析

为了掌握上下游水位、温度和时效等各种因素对坝基扬压力测孔水位的影响，选择典型年份（2014 年）的数据，计算和分析统计模型中各个组成部分的变化值占总变化量的比例。

除UP2 外，其他坝基扬压力测点数学模型均选中上下游水位分量，且其占比最高，说明上下游水位分量对坝基扬压力变化影响最大。在2014 年扬压力总变化量中，UP03、UP25、UP36、UP38、UP40、UP41 等测点上下游水位分量占扬压力变化量的44.41%～73.19%，其他测点的上下游水位分量占扬压力变化量的8.39%～37.46%。

在大多数扬压力测点数学模型中，温度分量占比居中，表明其对扬压力变化有着明显的影响。在2014 年扬压力总变化量中，UP11、UP25、UP27、UP29、UP36、UP38、UP40 等测点温度分量占扬压力变化量的7.15%～29.47%，其他测压管温度分量占扬压力变化量的31.58%～86.28%。

各扬压力测点数学模型均选中了时效分量，但其比例反映出时效分量对该重力坝坝基扬压力变化影响最小。在2014年扬压力总变化量中，UP13、UP26、UP27、UP33、UP37 等测点时效分量占扬压力变化量的47.45%～66.24%，剩余测压管时效分量占比相对较低，占扬压力变化量的2.21%～38.46%。

经分析，在影响该重力坝坝基扬压力变化的3 个因素中，上下游水位分量影响最大，温度分量居中，时效分量影响最小。由于该电站为日调节水库，影响最大的上下游水位全年变化不大，温度也保持比较稳定的周期性变化，而可能变化较大的时效分量则影响最小，因此可初步推断该重力坝坝基扬压力总体不会有太大的变化。

4 安全监控指标

4.1 安全监控指标制定方法

除了根据设计阶段各类计算成果提出的设计监控指标外，大坝运行期还需要根据安全监测资料的积累情况适时提出运行期监控指标。运行期监控指标一般可以通过综合比较法、置信区间估计法、典型效应量小概率法、结构计算法和可能不利荷载组合法来制定。根据该重力坝的特点和实际情况，采用置信区间估计法和典型效应量小概率法来制定安全监控指标。

（1）置信区间估计法

置信区间估计法首先需要建立扬压力测点的数学模型，然后使用数学模型的结果计算监测效应量（E^）与实测值E 的差值（E^-E）。该值有100（1-α）%的概率落在置信带Δ=±iS 范围之内，而且测值过程没有出现明显的趋势性变化，则可以认为运行时正常的，反之是异常的[3]。

根据该重力坝具体情况，参考其他同坝型、同规模工程经验，取显著性水平α 为5%，此时i 取值1.96，即Δ=±1.96S。此时，判别标准为：

①当（E^-E）＜1.96S，且测值过程没有出现明显的趋势性变化时，可认为该测点测值正常或安全。

②当（E^-E）≥1.96S 时，测值异常。

因此，相应监测效应量的监控指标为：Em=E^±1.96S。

（2）典型效应量小概率法

根据工程具体情况，从坝基扬压力的长期监测资料中，选择在不利荷载组合时的监测效应量Xmi，Xmi则为随机变量，由长期监测数据可以获得一个子样数为n 的样本空间：

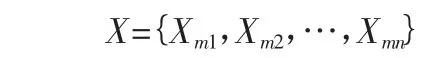
根据下式计算其平均值和标准差：

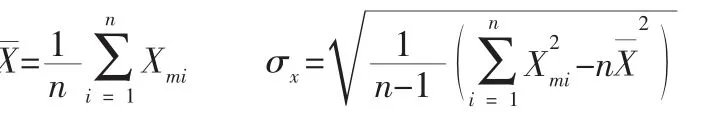
然后，用小样本统计检验方法，进行分布检验，以确定其概率密度f(x)的分布函数F(x)(如正态分布、对数正态分布以及极值I 型分布等)[4]。

假设Xm为监测效应量的极值，因此当X＞Xm时，大坝将要出现异常或险情，由分布函数可以计算出X＞Xm的概率为：

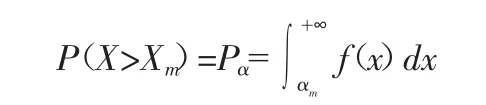
参考其他同坝型、同规模工程经验取失事概率Pα为5%，可由Xm的分布函数直接求出Xm=F-1（x，σx，α）。

4.2 安全监控指标确定原则

首先根据工程主副防渗帷幕及排水孔的布置形式，按照规范及设计计算参数，计算出扬压力测点的结构计算值。然后，根据置信区间估计法、典型效应量小概率法，分别计算扬压力测点监控指标，同时统计各测点的历史极值，将以上计算结果和统计值与结构计算值比较。当以上数值没有超过结构计算值时，取以上数值中的极值为安全监控指标。当以上数值超过结构计算值时，取结构计算值为安全监控指标。

4.3 扬压力安全监控指标

首先对各扬压力测点的数据质量进行评判，在此基础上选择UP 08、UP11、UP17、UP25、UP26、UP27、UP33、UP39、UP41、UP46 共9 个扬压力测点制定安全监控指标。接着根据上述制定方法和确定原则，计算制定扬压力测点安全监控指标，详见表4。

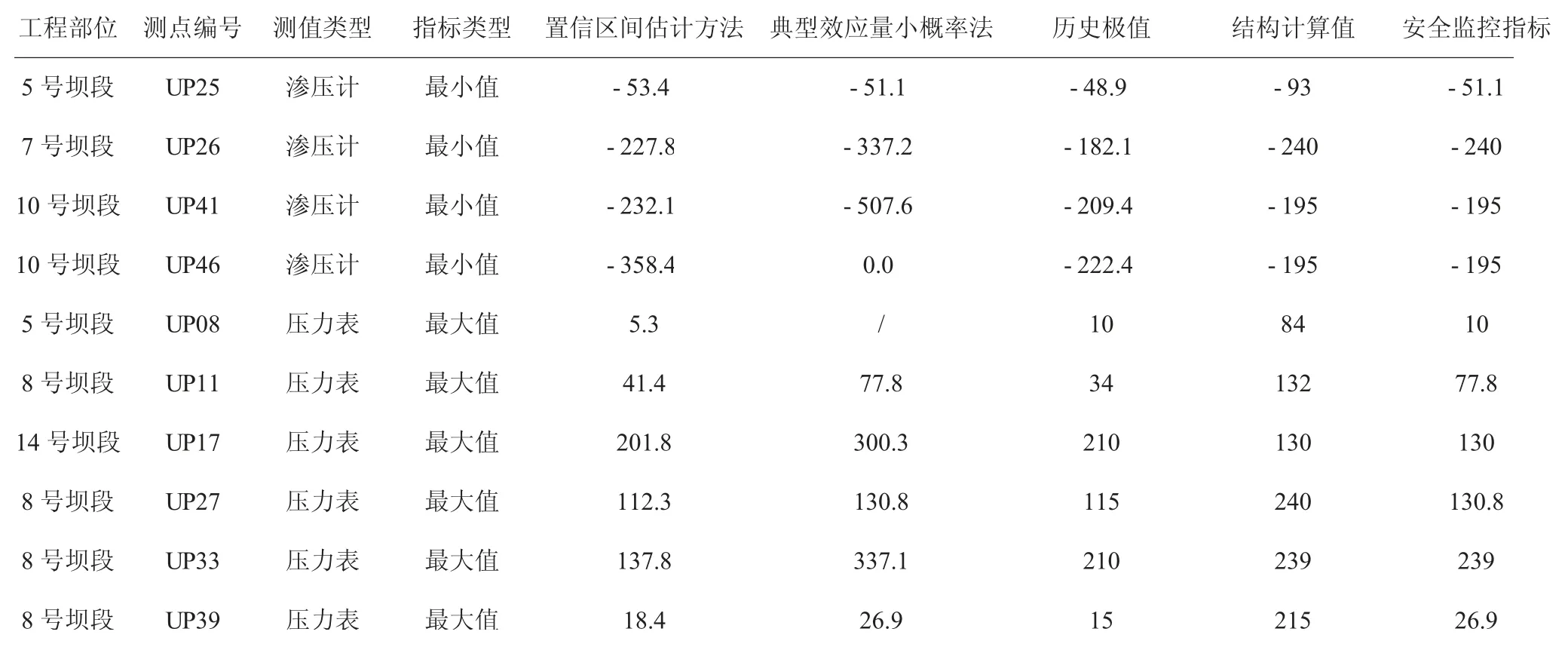
表4 扬压力测点安全监控指标统计表（单位：kPa）

由于该重力坝扬压力监测手段有渗压计和压力表两种，其中渗压计测值为负值时表示有压，因此选择最小值作为不利值，计算最小值作为安全监控指标；而压力表测值为正值时表示有压，因此选择最大值作为不利值，计算最大值作为安全监控指标。

扬压力测点UP25 置信区间估计法、典型效应量小概率法计算结果以及历史极值都未超过结构计算值，因此将选择计算结果和历史极值中的最小值作为安全监控指标。但由于UP25扬压力测点的数学模型复相关系数R＜0.8，置信区间与测值区间比例大于50%，因此置信区间估计法计算结果不作为监控指标依据，最终选用典型效应量小概率法计算结果作为UP25 测点安全监控指标。

当上述测点测值接近或超过安全监控指标时，应立即进行测值复测，增加观测频次，关注测值变化。如测值出现趋势性变化，应加强现场检查，并对监测数据进行分析和评估，必要时进行坝体渗流稳定复核结构计算，提出大坝运行控制要求。

5 结语

为充分运用GGQ 水电站重力坝坝基扬压力监测成果对大坝安全进行评估，定性分析了坝基扬压力的分布规律、UP09 扬压力系数偏高的原因，同时建立了坝基扬压力统计模型进行定量分析，得出了该重力坝坝基扬压力主要受上下游水位影响、主帷幕防渗效果良好、UP09 测值偏高不影响大坝安全等结论，最后通过置信区间估计法、典型效应量小概率法，制定了扬压力安全监控指标，为大坝运行期间的扬压力安全监测提供了科学依据。